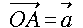 ,
,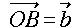 ,
,
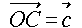 とします。
とします。Weekend Mathematics/コロキウム室/NO.165
| NO.1377 | 2003.4.1. | yokodon | 四面体と平行四辺形(5) |
〜(1)No.1285 模試S号外:四面体と平行四辺形〜
NO.1290 四面体と平行四辺形(2)で初等幾何的な、
NO.1312 四面体と平行四辺形(4)の後半でベクトルを用いた(2)の議論を拝見
しました。
一応、今更ながらですが、前半の(1)をベクトルで考えたらどうなるか?を述べ
させて下さい。
文字数が多くて泥臭いですが、力業でもちゃんと出来るということも数学では大事
だと思うので(私見)。
NO.1285 四面体と平行四辺形(1)の題意で、
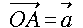 ,
,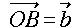 ,
,
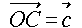 とします。
とします。
まず、各点の定義から以下が成り立ちますね。
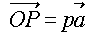 ,
,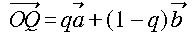 ,
,
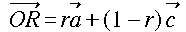 ,
, 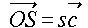 0 ≦ p, q, r, s ≦ 1
0 ≦ p, q, r, s ≦ 1
さて、条件(i)から、
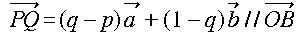
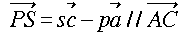
ですから、直ちに
p = q = s …[1]
を得ます。
次に、条件(ii)から、点Rは平面PQS上にあるので、ある実数α, β が存在して
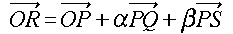
が成り立ちます。これに、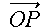 ,
, 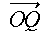 ,
,
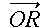 の式を代入し、[1] 式を用いて整理すると
の式を代入し、[1] 式を用いて整理すると
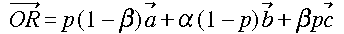
となります。これを、上記の [OR] の式と比較して、p が [0, 1] を任意に動くこと
に注意して
α=β=1 , r = 1 - p …[2]
を得ます。
以上から、各点の位置ベクトルは、
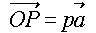 ,
,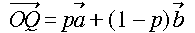 ,
,
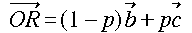 ,
, 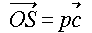 0 ≦ p ≦ 1
0 ≦ p ≦ 1
・・・と表せることが分かります。
このとき、
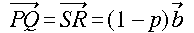
から、題意の主張(四辺形PQRSが平行四辺形であること)は成り立ちます。
なお、問(2)に関しては、上記の結果をそのまま準用すれば p の2次関数の最大
値問題に帰着します。

| NO.1378 | 2003.4.1. | yokodon | 隠れた円周(3) |
NO.1229 隠れた円周に関して、
NO.1311 隠れた円周(2)
で解析的な議論をしていただきました。
今回は、ちょっと初等幾何的な観点を入れた議論をしてみたいと思います。
点Cの直線OPに関する対称点をD、2直線CD、OPの交点をRとします。
このとき、Dは曲線 xy = 1 上に、また3点A,P,Dは同一直線上にあります。
更に、簡単な計算から
CR2 - OR2 = 2 、OA2 = AR2 - OR2 = 2
であることも分かります。
以上から、AR = CR = DR。即ち、3点A,C,DはRを中心とする円周上にあります。
このことと3点C,A,Qが同一直線上にあることから、以下を得ます。
∠DAC = ∠PAQ = π/2
同様の議論により、∠PBQ = π/2 を得ることが出来ます。
これより、「P,QはA,Bを直径の両端とする円周上にある」という主張は成り立ちます。
双曲線 xy = 1 を -π/4 (rad) 回転して、直線PQを y 軸に一致させてみると、見通しが良くなるかも知れません。

| NO.1379 | 2003.4.1. | yokodon | 最大・最小となる点(4) |
NO.1322 最大・最小となる点(2)訂正
今更ながらの漸くですが、NO.1319最大・最小となる点(1)
の問題2 に関する議論(NO.1322 での後半)で
、ニースケンスさんから戴いたコメント No.NO.1327 最大・最小となる点(3)
へのお返事です。
直線APとBCの交点をKとおくと、
(*) ⇔ S_0 = 3△PBC
⇔ AK = 3PK
ですから、Pは...
S0 = 3・△PBC = 3・△PCA ですから、点Pを通り辺BC、辺CAに平行
な直線を引いたときの各辺の交点を考えることにより、以下が成り立ちます。
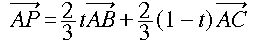
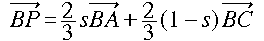 0 ≦ t, s ≦ 1
0 ≦ t, s ≦ 1
紙面節約のため端折りますが、上記両式を
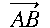 ,
,
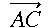 の一次結合に変形して係数を比較することで、
の一次結合に変形して係数を比較することで、
t = s = 1/2
を得ます。これより、直ちに「Pは三角形ABCの重心である」という結論を得ます。
#なんで、前回間違えたのだろう?(^^;

| NO.1380 | 2003.4.1. | yokodon | 立方体でないさいころ(3) |
僕も、kirkland さんの球面上の領域の面積を全球面の面積で割った値が所望の確
率を与えるものと考えます。
せっかくの平易な説明をわざわざ難しくするようで申し訳ないですが、「立体角」
という概念を導入すると、NO.1373 の図11 の球面上の面積は、点Oから見た長方形ABCDの立体角…に球の半径の2乗をかけた値…になります。
Oを原点とし、Oから平面ABC、平面CDH、平面ADHに下ろした垂線が z軸、x 軸、y 軸の正方向となるように座標軸をとり、立体角の値を計算してみましょう。その前に、「立体角とはなんぞや?」というのを説明しておきます。
step1:立体角とは?
面Sが点Oに対して張る立体角(又は、点Oから見た面Sの立体角)とは、Sを底面、Oを頂点とする錐面が、Oを中心とする半径1の球面から切り取る面積を意味します。Sが平面上の領域の場合はこれで話が済んでしまいますが、Sが曲面上の領域の場合は、これを微小部分に分けて考えます。
面S上の点をP、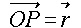 、Pを含む微小面積を dS 、Pにおける面Sの単位法線ベクトルを
、Pを含む微小面積を dS 、Pにおける面Sの単位法線ベクトルを 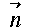 、
、
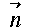 と
と 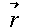 のなす角をθとすると、点Oからみた微小面の立体角 dΩ は、
のなす角をθとすると、点Oからみた微小面の立体角 dΩ は、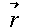 の大きさを r として
の大きさを r として
 ・・[1]
・・[1]
で与えられます。曲面Sの全立体角は、これを積分すれば計算できます。
#とは言え、ここで問題としているのは平面上の長方形なのですが、同じ考え方で計算できます。
step2:題意の面積を計算してみよう
一般の場合で考えてみましょう。Sとして、以下の長方形の領域を考えます。
S = {(x, y, z) | -a ≦ x ≦ a, -b ≦ y ≦ b, z = c}
対称性から、以下の長方形 S0 の立体角を求め、それを4倍すれば所望の立体角になります。
S0 = {(x, y, z) | 0 ≦ x ≦ a, 0 ≦ y ≦ b, z = c}
さて、面積要素は dS = dxdy にとれます。法線ベクトル 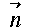 として、以下をとりましょう。
として、以下をとりましょう。
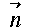 = (0, 0, 1)
このとき、ベクトルの内積の公式から
= (0, 0, 1)
このとき、ベクトルの内積の公式から
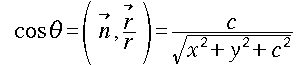 ・・[2]
・・[2]
よって、この [2] 式を [1] 式に代入して積分すれば、求める立体角Ω(S)は、S
の対称性に注意して以下のようになります。
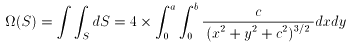
この計算をやっとこさ実行すると、以下の結果を得ます。
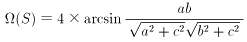
試しに数値計算してみましょう。
(a, b, c) = (2, 3/2, 5/2) を代入すると、
Ω(S) = 1.0388... ≒ 0.4166×π
です。
step3:さて、問題の確率は?
step2 の長方形Sの立体角Ω(S) を直方体全部の立体角(任意の球面をその中心から見た立体角に等しく、値は 4π)で割ると、所望の確率になります。計算すると、Ω(S)/4π = 0.10415... です。
なお、他の面に関しても同様に求めてみると、
3 cm × 5 cm の面が下の場合:0.15521...
4 cm × 5 cm の面が下の場合:0.24063...です。
因みに、立方体のさいころの場合を考えると、step2 で a = b = c の場合を考えれば容易に分かる通り、一つの底面をTとして、
Ω(T) = 4×Arcsin(1/2) = 2/3・π
ですから、面Tが下になる確率はめでたく
Ω(T)/4π = 1/6
・・・となるわけです。

| NO.1381 | 2003.4.1. | yokodon | 積分式の解(2) |
NO.1374 積分式の解に関して
NO.1374にある式は、
1次元の拡散方程式(∂C/∂t = D・∂2C/∂x2)の解ですね。
この式にある定積分を実行せよというのがご投稿の主旨だと理解しました。
この積分
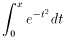 を x の関数として陽に書き出す
(三角関数や指数・対数関数、有限次数の多項式とかいった既知関数の積や合成の形
で表現する)ことは出来ないと思います。が、数値計算のために級数表示することな
ら可能です。
を x の関数として陽に書き出す
(三角関数や指数・対数関数、有限次数の多項式とかいった既知関数の積や合成の形
で表現する)ことは出来ないと思います。が、数値計算のために級数表示することな
ら可能です。
指数関数のマクローリン展開を用いて、まず以下のようにします。
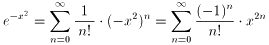
これを項別積分すれば、以下のようになります。
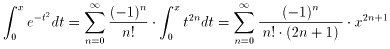
ここに、x → x/{2√(Dt)} の置き換えをすれば、所望の級数表示になります。
数値計算の目的で使うなら、級数表示は有用な式であると思います。

| NO.1382 | 2003.4.1. | 水の流れ | 人生模様(1) |
太郎さんの学校では、離任式が今年から3月の下旬に行われる終業式の中でありました。特に、担任のある場合は生徒の驚きは大変なものがあります。19年間在職されて、今年退職される先生の話の中で、「人生には、3つの坂があります。登り坂、下り坂、あと1つ皆さん、分かりますか?」生徒からは返事のないのを見計らって、「それは まさか の さか です。皆さん、この まさか に出会ったときに 動じることなく、人生を生き抜いてください。」大変ユニークな話でした。
ここで、問題です。
人生の中で、n個の登り坂とn個の下り坂に出会ったとします。
そうすると、どんなライフライン(人生模様)ができるでしょうか。
ただし、人生の始まりの地点から、決して下がらないとしてください。
例えば、n=1場合は、(登り、下り)は良いですが、(下り、登り)は起こらないとします。したがって、1通り。n=2場合は、(登り、登り、下り、下り)、(登り、下り、登り、下り)は良いが、
(登り、下り、下り、登り)、(下り、下り、登り、登り)などは起こらないとします。
したがって、2通りのライフライン(人生模様)があることになります。
問題1:n=3の場合は、何通りのライフライン(人生模様)になるか。
問題2:n=4の場合は、何通りのライフライン(人生模様)になるか。
問題3:一般に、何通りのライフライン(人生模様)になるか。nで示してください。

| NO.1383 | 2003.4.5. | kirkland | 人生模様(2) |
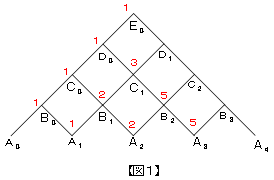
| 先生 | 先生「今回は、多くは語らんぞ。だから君も、ギャグなしでやりたまえ。問題1は、【図1】を見て数えなさい。」 |
| A君 | 「ギャグなしは、寂しいですね〜。n=3のときは、A0からA3まで行く道筋です。A0からB0までの道筋は1通りで、A1、C0までも1通りです。B1には、C0から来る場合とA1から来る場合があるので、1+1=2通りです。そんな感じで、その点までの道筋の数を書き込んでいったのが、赤の数字です。というわけで、5通りですね。」 |
| 先生 | 「よろしい。問題2についても、多くは語らんぞ。」 |
| A君 | 「同じように数字を書き込んでいってもいいんでしょうけど、図の対称性に注目すると、A0からA4に行くには、A2、C1、E0のいずれかを必ず通ります。A0からA2に行くのは2通りあります。図の対称性からA4からA2に逆行するのも2通りあって、逆に考えるとA2からA4に行くのも2通りです。というわけで、A0からA2に行く2通りの道筋のそれぞれに対して、A2からA4に行く道筋が2通りずつあるので、A0からA2を通ってA4に行く道筋は2×2=4通りです。C1、E0を通って行く場合も同様に、それぞれ3×3=9通り、1×1=1通りです。従って、合計4+9+1=14通りですね。」 |
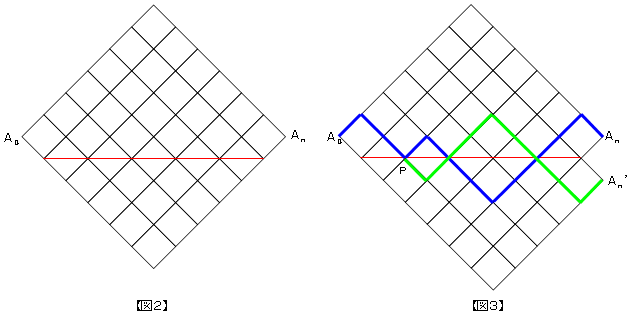
| 先生 | 「よいよい。問題3は、少しヒントをあげよう。直接数えると大変なので、【図2】のように、人生の始まりの地点よ り下ってもいいことにしよう。」 |
| A君 | 「ほほう。すると、A0からAnへ行くすべての道筋の数から、人生がマイナスになってしまう不幸な道筋(【図2】で、 赤線に触れてしまう道筋。以下、不幸な道筋と呼ぶことにしま〜す)の数を除けばいいんですね。」 |
| 先生 | 「その通り。例えば、【図3】の青線のように進んだとしよう。これだと点Pで初めて赤線に触れてしまうわけだ。 点P以降の道筋を赤線で折り返したのが、緑線だ。2,3実験してみればいいと思うよ。」 |
| A君 | 「すべてAn’に到着しますね。不幸な道筋は、初めて赤線に触れてしまう点以降を赤線で折り返せば、必ずAn’に 到着するんですね。An’は赤線について対称だからですか?。しかしまあ、突飛な考え方ですねぇ。」 |
| 先生 | 「これは、君が知らないだけで有名な話だ。とにかく、細かいことは語らん。」 |
| A君 | 「というわけで、不幸な道筋の数は、A0からAn’へ行く道筋の数と同じですね。ところで、考え方は十分わかった のですが、実際それぞれの道筋の数は、どうやって計算するんですか?」 |
| 先生 | 「具体例を挙げながらやっていけば、小学生の君でも理解できないこともないんだが、今回は、多くは語らんことにしたので、答えだけだ。A0からAnへの道筋の数は2nCn、A0からAn’への道筋の数は2nCn−1で、この差が、求める数だ。」 |
| A君 | 「はっきり言って、Cとか言われても意味プーです。」 |
| 先生 | 「だから、今回は多くは語らんと言っただろう。また、今度教えてあげよう。」 |
| A君 | 「語らん、語らんってしつこいですけど、何かのまじないですか?ところで先生、4月になったんだから、僕はもう中学1年生のはずなんですけど?」 |
| 先生 | 「細かいことを気にしちゃあダメだ。そもそもの設定がおかしくなってしまうだろ!それについても、多くは語らん!そもそも、のび太君もずっと小学生のままじゃないか。まぁ、落第したということにしておけば?」 |

| NO.1384 | 2003.4.7. | wasmath | 整数問題(5) |
(一部修正 4/8 7:00)
コロキウム室NO.877 整数問題にある
「a,bを自然数とするとき, a2+b2がabで 割り切れるための必要十分条件は a=b である」について、 少し興味をひいたので,若干拡張した命題として, 当時の証明とは別の方針で証明してみました。
命題
a,bを正の整数、nを2以上の整数、kを0<k<n
なる整数とするとき、
an+bnがakbn-kで
割り切れるための必要十分条件はa=bである。
証明
十分性は明らかであるから、必要性だけ示せばよい。
an+bnがakbn-kで
割り切れるとすれば、
an+bn=makbn-k
(mは正の整数)
と表される。gcd(a,b)=dとおくと、
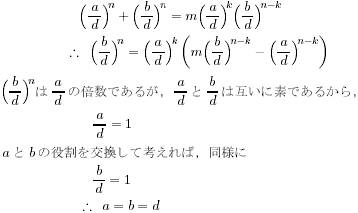
(証明おわり)

| NO.1385 | 2003.4.11. | Hkeisuke | 最速降下問題(17) |
自分も何か問題を進展させて投稿したかったのですが、ほとんど進まず、時間がたってしまいました。
シンプレクティック積分法なんですが、
計算物理のためのC/C++言語入門/Symplectic数値積分法
に解
説がありました。あと、まだ読んでいませんが、現代物理学叢書 力学 大貫義郎・吉田春夫著にものっていました。数理科学1995年6月号のほうも、学校で少し見てみました。まだ数値計算も入門したばかりなので、これからこの問題を通していろいろと勉強していこうと思います。自分にはまだシンプレティック積分法、他ほとんどの数値積分法が使いこなせないので、手始めに、1次のシンプレクティッ
ク法でやってみました。ここに載せられるほどしっかりとやっていないのでグラ
フは次の機会にしたいと思いますが、いろいろとパラメータを変えてもサイクロ
イドに似たようなものになりました。他に、2つばかり違ったことを考えてみま
した。ひとつは、DDTさんの使っているパラメータαの微分dαを時間tの微
分dtと関係づけることです。こうすれば、時間経過による動きがわかっていい
かと思います。この問題でのラグランジアンは、dtと、dξ、dθの間の関係
式と見ることもできるので、それにNO.1356
最速降下問題(16) の(1)式を代入する
と、dαとdtの関係が得られ、同じく(1)式のdαをdtで置き換えればで
きます。この部分でラグランジアンを出してきてもいいのかということが少し引っ
かかりましたが、いけないという理由も見つからなかったので、やってみました。
もうひとつは、ゴールドスタインの「力学」を読んでいて、運動の拘束に関する
章があったのですが、この最速降下線も一種の拘束なのではないかと思い、そこ
に載っていた方法をやってみたことです。。拘束するものがなければ万有引力下
では2次曲線を描くのですから、そういうことになりますよね?
そう考え、DDTさんの導き出したNO.1354 最速降下問題(14) の(28)*式と、Lagrangeの未定乗数法を使って何か新しい情報が得られないかとやっているところです。式が複雑なので、まずは普通の最速降下線のときにやってみようとも思っています。いつも報告みたいなものしかできなくて申し訳ないんですが、そのうちしっかりと話を展開してみたいです。

| NO.1386 | 2003.4.12. | Junko | 「天才の栄光と挫折」 |
新潮社から出ている藤原正彦先生の「天才の栄光と挫折」を読みました。
この本の紹介文を引用します。
ニュートン、関孝和、ガロワ、ハミルトン、コワレフスカヤ、ラマヌジャン、チューリング、ワイル、ワイルズ。いずれおとらず、天才という呼称をほしいままにした九人の数学者たち。が、選ばれし者ゆえの栄光が輝かしくあればあるほど、凡人の何倍もの深さの孤独や失意に、彼らは苦悶していたのではないか。同業ならではの深い理解で綴る錚々たる列伝。
偉大な数学者たちの人間らしい面を知り、よりいっそうその偉大さを感じました。
是非おすすめの1冊です。

 E-mail
E-mail
 戻る
戻る