
Weekend Mathematics/コロキウム室/NO.155
| NO.1307 | 2002.10.9. | katu | 複素数の定義(3) |
かなり答えにくいものなのかもしれません。
自分の理解の中では、数に関する集合などはDDTさんが書いていたように「拡張」
という表現がぴったり来るのだと思います。
「自然数→整数→有理数→実数→複素数」という拡張を行っています。
加減の演算を閉じるために整数へ
乗除の演算を閉じるために有理数へ
という感じです。
残り実数と複素数というのは、演算というよりも、有理数までで足りない部分を補う
ために作られた(?)ものなんだと思います。
だから、実数・複素数については演算は後から加えた(?)ものである。と考えま
す。
つまり現在ある演算(俗にいう四則)を用いることによって実数・複素数の演算を定
義した。そのときに重要なのが「演算が閉じられている」ということです。
それを考慮に入れると実数での加法を利用して複素数の加法を定義することはとても
自然なことだと思います。
少し違う観点から言うと、複素数は複素数平面であらわすことが出来ます。これはと
うぜん2次元平面と同様に扱うことが出来ます。つまりa+bi→(a,b)。これは高校で
もやりますね。つまり複素数の集合CはR×Rと同じであるということです。平面上
(ベクトル)で加法はそれぞれの要素の加法ですよね。つまり複素数上での
(a+bi)+(c+di)=(a+c)+(b+d)iに他ならないわけです。
ちょっと蛇足ですが、演算といっても結局は写像のことです。二つの要素から1つの
要素出すんですから・・・。その考えからいくと定義は自然ではないでしょうか・・
・。
と、漠然と文字を羅列してしまったみたいですが、なかなかわかりにくいですよね。
複素数はもともとこの世の中(自然世界)に存在しない数なんですから定義が変だと
思ったりもするかもしれないですよね。
代数学の先生は複素数についてこんなことを言ってました。それを最後に書いておき
ます。
複素数が存在するかどうかは自然界にないのでわからないそうです。
では、なぜ複素数を普通に使うことが出来るかというのは、次の事実があるからなん
だそうです。
「複素数全体の集合Cは1変数多項式環のX2+1による商集合と同相である」
ということからこの商集合の元Xがまさに虚数単位iと対応するため、Cを使うことが
出来るんだそうです。
これはガロア理論をやったことがあると知られた話だったような気もします。(結構
昔なのであやふやです。)

| NO.1308 | 2002.10.9. | yokodon | 四面体と平行四辺形(3) |
計算量は些か多くなりますが、
位置ベクトルを用いた議論をお奨めしたいところです。
別解を考えてみてください。

| NO.1309 | 2002.10.11. | ニースケンス | 複素数の定義(4) |
"a+bi"というのは、実数の順序対(a,b)により定まる複素数を表す、
全体で1つの記号です。
複素数の加法・乗法などを定義すると、"a+bi"で表される複素数は、
実数aに実数bと虚数iの積を加えたものに等しいので、"a+bi"の"+"と、
複素数の加法を表す"+"を混同してよいし、"bi"をbとiの積だと思ってよい、
ということです。
紛らわしければ、複素数を"(a,b)"と表記しておけばよいでしょう。

| NO.1310 | 2002.10.12. | Junko | 平方数の逆数の和(3) |
ゼ−タ−関数ですね。
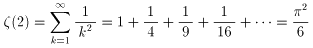
これについて、 テ−マ別の部屋の中に、
ゼ−タ−関数物語としてまとめてあります。

| NO.1311 | 2002.10.12. | Junko | 隠れた円周(2) |
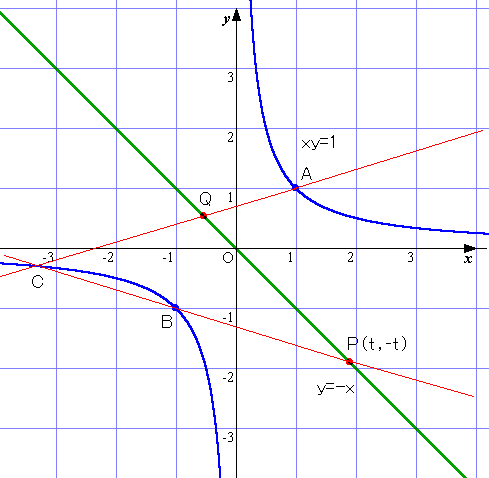
仮定より、t≠1、t≠-1、t≠0
直線y=-x上の点P(t,-t)とおくと、直線BPは、
(t+1)(y+1)+(t-1)(x+1)=0
これと、双曲線xy=1を連立させることにより、点B以外の交点Cの座標を求める。
C((t+1)/(-t+1),(-t+1)/(t+1))
次に直線ACの傾きを求めると、(t-1)/(t+1) なので、方程式は
(t+1)(x+1)+(t-1)(x-1)=0となる。
これと、直線y=-xを連立させることにより、点Qの座標を求める。
Q(-1/t,1/t)
PQを直径とする円の方程式を求めてみます。
PQの中点の座標は、
((t2-1)/2t,(-t2+1)/2t)
半径rは、
r=(1/2)PQ=√2(t2+1)/2t
従って、円の方程式は、
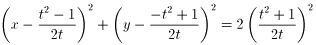
点A(1,1)を代入すると成立することから、
点A,点Bは円周上に存在することがわかる。
(点Aと点Bは、直線y=-xにより対称であることから、一方を調べれば十分)
というわけで、ひたすら座標を用いて計算しました。

| NO.1312 | 2002.10.12. | Junko | 四面体と平行四辺形(4) |
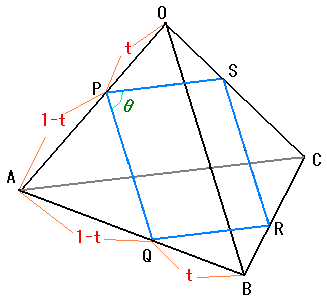
(2)四辺形PQRSの面積が最大になるのは、どのような場合か。
NO.1290のBossF さんと同じように、
OP:PA=t:1-t (0<t<1) とします。
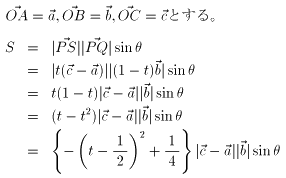
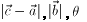 は定数なので、
t=1/2で面積が最大になるということがわかる。
は定数なので、
t=1/2で面積が最大になるということがわかる。

| NO.1313 | 2002.10.12. | 中川 幸一 | Lemniscate |
座標平面上の双曲線
x2-y2=1
上に点Pをとりその点における接線を引く。原点Oからその接線に垂線を引きその足を
点Qとする。点Pが双曲線上を動くとき点Qの軌跡を求めよ。
この問題の答えを解くとかの有名なLemniscateが出来ます。
これは有名事実らしいです。
NO.1229 隠れた円周
という問題を見て双曲線が出ていたので、紹介しておきます。

| NO.1314 | 2002.10.12. | 小学名探偵 | 等脚台形の定義 |
「等脚台形の定義は、台形の特徴を持っていて、更に二つの対角線の長さが一緒」です。(中学受験ズバピタ算数図形の48ページ)
isosceles triangleは二等辺三角形(等脚三角形),isosceles trapezoid は等脚台形です。と言うことで、等脚台形は二等辺三角形の頭(相似の小さいの)を取り外して出きる形と言うイメージなのですが。父がアメリカyahoo で define isos.trapezoid で調べたところ、相対する2辺が平行で残る2辺が等しく対角の角度の和が,180度になる、というようなのが多かったそうです。

| NO.1315 | 2002.10.15. | 中川 幸一 | 座標軸の回転移動 |
座標軸を原点のまわりにθだけ回転すると
(1)
x=X cos θ - Y sinθ
y=X sin θ + Y sin θ
iff
X=x cos θ + y sin θ
Y= -x sin θ + y cos θ
(2)
曲線 f (x , y) = 0→f ( X cos θ - Y sin θ , X sin θ - Y cos θ ) = 0
特別角の回転公式
(ア) θ=π/4 : x = ( X - Y )/√2 , y = ( X + Y )/√2
(イ) θ=π/6 : x = ( (√3) X - Y )/2 , y = ( X + (√3) Y )/2
(ウ) θ=π/3 : x = ( X - (√3) Y )/2 , y = ( (√3) X + Y )/2
例
xy=k2:座標軸を原点のまわりに45°回転すると X2-Y2=2k2
こうすると直角双曲線の式も見慣れた双曲線の式になることが分かります。

| NO.1316 | 2002.10.21. | 水の流れ | 多項式 |
* 太郎さんは、本年度の入試問題を眺めていたところ、早稲田大学にでていた問題を下のようにアレンジしました。皆さん、チャレンジください。


 E-mail
E-mail
 戻る
戻る