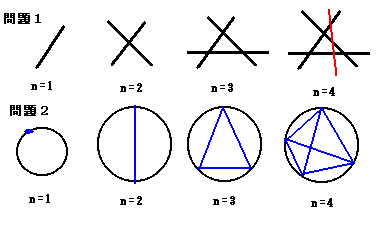
Weekend Mathematics乛僐儘僉僂儉幒乛NO.144
| NO.1228 | 2002.7.1. | 悈偺棳傟 | 墌傪暘妱 |
懢榊偝傫偼丄乽悢妛A乿偺嫵壢彂偱師偺傛偆側栤戣傪傛偔尒偐偗傑偡丅
栤戣侾丗暯柺忋偵値杮偺捈慄偑偁傝丄偳偺2杮傕暯峴偱側偔丄
傑偨丄偳偺3杮傕摨堦偺揰傪捠傜側偄傕偺偲偡傞丅
偙偺偲偒丄偙傟傜偺値杮偺捈慄偵傛偭偰暯柺偑倎値屄偺椞堟偵暘偗傜傟偨偲偡傞偲丄
乮侾乯悢楍乷倎値乸偵偍偄偰丄嵟弶偺6崁傪媮傔偰偔偩偝偄丅
乮俀乯悢楍乷倎値乸偵偍偄偰丄堦斒崁倎値傪値偺幃偱昞偟偰偔偩偝偄丅
偝偰丄摨偠傛偆側偙偲傪墌偺拞偱峫偊偰傒傞偙偲偵婥偑偮偒傑偟偨丅
栤戣俀丗墌廃忋偵値屄偺揰偑偁傝丄偦偺偡傋偰偺慻傒崌傢偣偑慄偱寢偽傟偰偄傑偡丅
偨偩偟丄撪晹偺揰偱3杮埲忋偺慄偑岎嵎偟側偄傛偆偵丄
偦偺揰偑寢偽傟偰偄傞傕偺偲偡傞丅偙偺偲偒丄偙傟傜偺捈慄偵傛偭偰丄
墌偺撪晹偑倐値屄偺椞堟偵暘偗傜傟偨偲偡傞偲丄
乮侾乯悢楍乷倐値乸偵偍偄偰丄嵟弶偺6崁傪媮傔偰偔偩偝偄丅
乮俀乯悢楍乷倐値乸偵偍偄偰丄堦斒崁倎値傪値偺幃偱昞偟偰偔偩偝偄丅

| NO.1229 | 2002.7.6. | yokodon | 塀傟偨墌廃 |
柾帋僔儕乕僘11
憃嬋慄 xy 亖 1 偺僌儔僼忋偵俀掕揰俙 (1, 1) , 俛 (-1, -1) 傪偲傞丅捈慄 y 亖
-x 忋偺揰俹乮扐偟丄俹偼 (-1, 1) , (1, -1) , 媦傃尨揰偲偼堎側傞傕偺偲偡傞乯偵
懳偟偰丄捈慄俛俹偲偙偺憃嬋慄偲偺岎揰傪俠乮俛偲偼堎側傞傕偺偲偡傞乯丄捈慄俙俠
偲捈慄 y 亖 -x 偲偺岎揰傪俻偲偡傞丅偙偺偲偒丄俀揰俙,俛偼慄暘俹俻傪捈宎偲偡傞
墌廃忋偵懚嵼偡傞偙偲傪帵偣丅

| NO.1230 | 2002.7.9. | yokodon | 嬻娫忋偺墌傪摦偔俀揰乮俁乯 |
崱峏側偑傜偱偡偑丄NO.1196偺惓夝傪敪昞偟偨偄偲巚偄傑偡丅
NO.1204 偺 DDT 偝傫偼丄偄偄慄傪峴偭偰偄傞偲巚偄傑偡丅
偨偩丄杮栤偺応崌丄揰俹偺慡懱偑昤偔恾宍偼嬋慄偱偡丅
俻 (cos兛, sin兛, 0) 偲偍偔偙偲偵偟傑偡丅
捈慄俹俻偲 xz 暯柺偺岎揰偑揰俼偱偡偐傜丄俼 (X, 0, Z) 偲偡傞偲丄偁傞幚悢 t
偑懚嵼偟偰丄埲壓偑惉傝棫偪傑偡丅
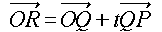 丒丒丒[1]
丒丒丒[1]
丂偙傟傪惉暘偱彂偔偲丄埲壓偺傛偆偵側傝傑偡丅
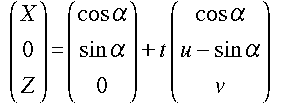 丒丒丒[2]
丒丒丒[2]
偙傟偺 y 惉暘偐傜丄
丂丂t 亖 sin兛/(sin兛 - u)丂丒丒丒[3]
偙傟傪丄[2] 幃偺 x 惉暘偲 z 惉暘偵戙擖偟偰丄
丂丂X 亖 (1 - t)丒cos兛 亖 u丒cos兛/(u - sin兛)
丂丂Z 亖 tv 亖 v丒sin兛/(sin兛 - u)丂丂丂丂丂丂丒丒丒[4]
[4] 偺俀幃傪 cos兛丄sin兛 偵偮偄偰夝偒丄兛 傪徚嫀偟偰惍棟偡傞偲師幃傪摼傑偡丅
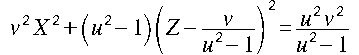 丒丒丒[5]
丒丒丒[5]
丂[5] 幃偑 xz 暯柺忋偺墌偲側傞偨傔偺忦審偼丄
丂丂v2 亖 u2 -1 妿偮 u2丒v2/(u2 - 1) 亜 0
偱偡偑丄壖掕偐傜 u 亜 1 偱偡偺偱忋婰戞俀幃偼帺摦揑偵惉傝棫偪傑偡丅
媡偺媍榑偼丄墘廗栤戣偵巆偟偰偍偒傑偟傚偆丅
偲偄偆傢偗偱丄媮傔傞娭學幃偼丄
丂丂v2 亖 u2 -1, u 亜 1丂乧(摎)
偱偡丅俹偺昤偔嬋慄偼丄廬偭偰憃嬋慄偺堦晹偱偡丅
傑偀丄妋偐偵帋尡偺栤戣偲偟偰偼丄側偐側偐戝曄偱偡丅夁嫀丄壗搙偐偛徯夘偟偨栤
戣傕丄崅峑俁擭乣偦偺忋偺庴尡惗帪戙偵懱尡偟偨偲偒偺亀巚偄弌偺栤戣亁偱偡丅偨偩
丄偄偞戝妛偱偺杮奿揑側妛栤偵岦偗偰偲側傞偲丄偁傞掱搙偺栤戣側傜壗偲偐偙側偣傞
榬椡偺偁傞妛惗偑梸偟偄偲偄偆偺偼丄戝妛懁偺杮壒偱偟傚偆偹乮偐偲偄偭偰丄嬌抂偵
擄偟偔偟偰傕丄嬌抂偵悢妛偺晄摼庤側妛惗偑擖妛偟偰偟傑偄丄岞暯側妛廗摓払搙偺敾
掕偵側傜側偄偲偄偆乬栤戣乭傕偁偭偨傝偟傑偡偑乯丅
丂悢妛傪娷傔偨峀偄堄枴偱偺悢棟壢妛偺慺梴偲婎慴揑擻椡傪梴偭偰傕傜偆偨傔偵偼丄
楙廗栤戣傪捠偟偰悢妛偺峫偊曽偵姷傟偰傕傜偆偺傕乧彮側偔偲傕杔掱搙偺杴恖偵偼乧
昁梫側傢偗偱偡偑丄偐偲尵偭偰庴尡梡偵摿壔偣偢偵偦傟傪傗傠偆偲偡傞偲丄傎傏昁慠
揑偵擄堈搙愝掕偺帋峴嶖岆偵娮傞傢偗偱丄偦偺慄堷偒偼側偐側偐擄偟偄偲偙傠偱偡偹丅
丂偦傟偱傕丄摢偺懱憖偲偟偰丄庯枴偱悢妛傪妝偟傓暘偵偼丄偁傞掱搙僎乕儉姶妎偱偦
偺乽擄偟偝傪妝偟傓乿偺傕傑偨僆僣側偺偱偼側偐傠偆偐乧偲巚偆偙偲傕弌棃傞傢偗偱
丄偙偙偱偼傑偀偦偆偄偆偙偲偵偟偰偍偒傑偟傚偆偐丅堦楢偺僔儕乕僘偼丄偦偆偟偨庯
巪偱偛徯夘抳偟偰偍傝傑偡丅

| NO.1231 | 2002.7.20. | yokodon | 暋慺悢偺晹暘廤崌乮侾乯 |
柾帋僔儕乕僘崋奜
暋慺暯柺偺晹暘廤崌偲偟偰丄埲壓偺俆偮偺廤崌傪峫偊傞丅
扐偟 z 偼暋慺悢丄z*偼偦偺嫟栶丄i 偼嫊悢扨埵傪昞偡丅
俙亖 {z | (z + z*)/2 偑 併2 偺惍悢攞}丆
俛亖 {z | (z + z*)/2 偑 併3 偺惍悢攞}丆
俠亖 {z | (z - z*)/2i 偑 併2 偺惍悢攞}丆
俢亖 {z | (z - z*)/2i 偑 併3 偺惍悢攞}
俤亖 (俙伩俠)伨(俙伩俢)伨(俛伩俠)伨(俛伩俢)
俤偐傜擟堄偺 17 屄偺尦傪庢傝弌偟偰嶌偭偨廤崌傪俥偲偡傞偲偒丄俥偺俀揰偺拞揰
傪偲傞偲偦傟偑俤偺尦偵側偭偰偄傞傛偆側俥偺尦偺慻偑昁偢懚嵼偡傞偙偲傪徹柧偣傛丅
#僶僀僩愭偱尒偐偗偨栤戣偱偡丅

| NO.1232 | 2002.7.21. | 拞愳丂岾堦 | 墌悕懁柺偺搳塭乮侾乯 |
倶倷倸嬻娫偵丄懁柺傪曣慄偱揥奐偡傞偲敿墌偱丄掙柺偺曽掱幃偑
倶2亄倷2亖倰2
偲側傞丄墌悕偺懁柺俽傪峫偊傞丅
偙偺偲偒丄俽傪捀揰偲揰(0,-r,0)傪寢傇曣慄偱丄捀揰偲揰(0,r,0)傪摦偐偝偢偵揥奐
偡傞丅
偱偒偨恾宍傪揰(0,0,+亣)偐傜丄倶倷暯柺偵搳塭偟偰偱偒偨恾宍傪俥偲偡傞丅
偙偺偲偒丄恾宍俥偺嬋慄俠偺曽掱幃傪媮傔傛丅

| NO.1233 | 2002.7.21. | 悈偺棳傟 | 掕愊暘乮侾乯 |
懢榊偝傫偼丄偙偺壞曗廗偱乽悢妛嘨偺擖帋栤戣乿傪夝愢偡傞梊掕偱偡丅師偺俀栤傪峫偊偰偔偩偝偄丅
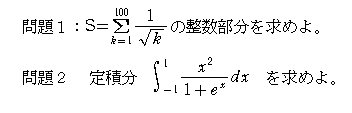

| NO.1234 | 2002.7.24. | BossF | 掕愊暘乮俀乯 |
(1)
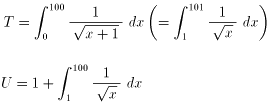
偲偍偔偲丄僌儔僼傛傝柧傜偐偵 T亙S亙U 偱偡丅偲偙傠偑
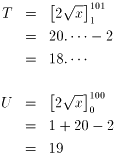
偱偡偐傜丄S偺惍悢晹暘偼 18 仭
(2)傑偢丄堦斒偵
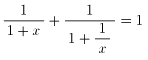 偱偁傞偙偲偵拲堄偟傑偡丅
偱偁傞偙偲偵拲堄偟傑偡丅
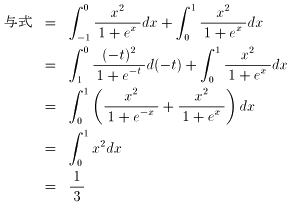

| NO.1235 | 2002.7.24. | BossF | 墌悕懁柺偺搳塭乮俀乯 |
NO.1232偵偍偄偰丄
乽俽傪捀揰偲揰(0,-r,0)傪寢傇曣慄偱丄捀揰偲揰(0,r,0)傪摦偐偝偢偵揥奐偡傞丅乿偲偁傝傑偡偑丄偙偺忦審偩偗偩偲揥奐偟偨懁柺乮敿墌乯偼捀揰偲揰(0,r,0)傪捠傞捈 慄傪幉偵夞揮偟偨偳偺埵抲偵傕偙傟傞偐傜丄F偼偒傑傜側偄傫偱偼丠
埲壓偼揥奐偟偨懁柺亖敿墌偺捈宎偑 x-y 暯柺偲暯峴偱偁傞偲偟偨帪偺夝偱偡丅
[夝]
傑偢曣慄偺挿偝R傪媮傔傑偡丅
2兾r=兾R 傛傝丂R=2倰
偡傞偲丄揥奐偟偨懁柺偺 x-y 暯柺傊偺惓幩塭偼挿幉 4r 抁幉 2r 偺懭墌偺敿暘偵側傝傑偡丅
亪C; x2/16+y2/4=r2,z=0 (y亞0)媦傃 y=z=0(lxl亝4R)

| NO.1236 | 2002.7.24. | BossF | 暋慺悢偺晹暘廤崌乮俀乯 |
A偺尦偱偁傞偙偲傪丄e(A)偲昞偡偙偲偵偟傑偡丅
傑偨丄m,n偼擟堄偺惍悢,x偼擟堄偺幚悢偲偟傑偡丅
戣堄傛傝
丂丂e(A)=併2n+xi
丂丂e(B)=併3n+xi
丂丂e(C)=x+併2ni
丂丂e(D)=x+併3ni
偱偡偐傜
丂丂e(A伩C)=併2m+併2ni
丂丂e(A伩D)=併2m+併3ni
丂丂e(B伩C)=併3m+併2ni
丂丂e(B伩D)=併3m+併3ni
偙偺倣丄値傪惍悢惉暘偲偄偆偙偲偵偟傑偡.
偝偰丄e(A伩C)傪倣丄値偺嬼婏惈偵傛偭偰暘椶偡傟偽4捠傝
e(A伩C),e(A伩C),e(A伩C)傕摨條偱偡偐傜慡晹偱16捠傝丅
偡傞偲E偐傜17 屄偺尦傪庢傝弌偟帪丄
彮側偔偲傕2偮偼忋偺暘椶偱摨偠強偵擖傝傑偡
偦偺擇偮偺拞揰傪峫偊傞偲嬼婏惈偺堦抳偐傜
摨偠暘椶偺偲偙傠偵擖傝傑偡丅丂丂丂丂仭

| NO.1237 | 2002.7.24. | 拞愳丂岾堦 | 儖僕儍儞僪儖懡崁幃 |
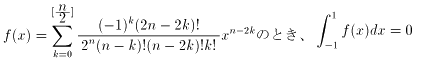
偲側傞偙偲偼偳偺傛偆偵徹柧偡傟偽傛偄偺偱偡偐丠
乮偙傟偼儖僕儍儞僪儖懡崁幃偺桳柤帠崁偩偦偆偱偡丅乯

| NO.1238 | 2002.7.24. | 拞愳丂岾堦 | 悢楍偺堦斒崁 |
堦晹廋惓7/26丂7:30
f(1)=2, f(n+1)=1/f(n) + 2/(n+1) 偙偺偲偒丄悢楍 f(n) 傪媮傔傛丅乮扐偟丄値伕俶乯
悢妛揑婣擺朄傪梡偄偰夝偗丅丂偲偄偆栤戣偩偭偨偺偱偡偑丄偦傟偱偼偍傕偟傠傒偑側
偄偺偱悢妛揑婣擺朄傪梡偄偢偵夝偗側偄偐偲巚偄傑偟偰乧丅
偪側傒偵悢楍偺夝摎偼丂f(n)=(n+1)/n丂偺偼偢偱偡丅

 E-mail
E-mail
 栠傞
栠傞