Weekend Mathematics／コロキウム室／NO.152

コロキウム室



NO.1283 2002.9.1.にゃんこ（二暗刻）コラッツの問題（２）

Ａ-2． 2p(1) ＜ (3/2)m(1)　で q1 が n0 より大きければこれまでと同じ作業を繰り返すことにする。
K,q の添数字や、m,p の 括弧内数字は作業回数を示すものとする。
k1,k2,・・,m(1),m(2),・・ 等
最初の奇数を n0 とし 3 倍して 2 で割る処理を m(1) 回して初めて偶数 nm(1) となるものとすれば、
（これまでは「3 倍して 2 で割る処理」を２つの作業としてきたが、今後は１つの作業として扱う）
　

(1) n0 = k12m(1) - 1 のとき　nm(1) = 3m(1)k1 - 1　となる。
　　　q1q1 を奇数として nm(1) = q12p(1) とおけば
　　　nm(1)+p(1) = q1　, k1 = (q12p(1) + 1)/3m(1)
　　　n0 = 2m(1)(q12p(1) + 1)/3m(1) - 1= (q12m(1)+p(1) + 2m(1))/3m(1) - 1
　　　q12p(1) = 3m(1)(n0 + 1)/2m(1) - 1 = (n0 + 1)(3/2)m(1)- 1
　　　q1 = { (n0 + 1)(3/2)m(1) - 1}/2p(1)
　　　∴　nm(1)+p(1) = { (n0 + 1)(3/2)m(1) - 1}/2p(1) = (n0 + 1)(3/2)m(1)2-p(1) -2-p(1)
　　　1回目の一連の作業が終わって q1 が求められその増減数z1 は

z1 = q1- n0 = (n0+1)(3/2)m(1)2-p(1)-2-p(1) - n0 　
=n0 {(3/2)m(1)2-p(1) - 1} + (3/2)m(1)2-p(1) - 2-p(1)

(2) nm(1)+p(1) = k22m(2) - 1 のとき　nm(1)+p(1)+m(2) = 3m(2)k2 - 1　となる。
　　　q2 を奇数として nm(1)+p(1)+m(2) = q22p(2) とおけば
　　　nm(1)+p(1)+m(2)+p(2) = q2, k2 = (q22p(2) + 1)/3m(2)
　　　nm(1)+p(1) = 2m(2)(q22p(2) + 1)/3m(2) - 1= (q22m(2)+p(2) + 2m(2))/3m(2) - 1
　　　q22p(2) = 3m(2)(nm(1)+p(1) + 1)/2m(2) - 1 = (nm(1)+p(1) + 1)(3/2)m(2) - 1

q2 = (nm(1)+p(1) + 1)(3/2)m(2)2-p(2) - 2-p(2)
= {(n0 + 1)(3/2)m(1)2-p(1) - 2-p(1) + 1}(3/2)m(2)2-p(2) - 2-p(2)
= (n0 + 1)(3/2)m(1)+m(2)2-p(1)-p(2) - (3/2)m(2)2-p(1)-p(2) + (3/2)m(2)2-p(2) - 2-p(2)

　　　2回目の一連の作業が終わって q2 が求められその増減数z2 は

z2 = q2 - q1 = (n0 + 1)(3/2)m(1)+m(2)2-p(1)-p(2)
　　 - (3/2)m(2)2-p(1)-p(2) + (3/2)m(2)2-p(2) - 2-p(2) - {(n0 + 1)(3/2)m(1)2-p(1) -2-p(1) }
= (n0 + 1)(3/2)m(1)2-p(1) {(3/2)m(2)2-p(2) - 1}- (3/2)m(2)2-p(1)-p(2) + (3/2)m(2)2-p(2) - 2-p(2) + 2-p(1)
= (n0 + 1)(3/2)m(1)2-p(1) {(3/2)m(2)2-p(2) - 1} + (3/2)m(2)2-p(2) {1 - 2-p(1)} - 2-p(2) + 2-p(1)

　　　最初からの増減数z は

z = q2 - n0
= (n0 + 1)(3/2)m(1)+m(2)2-p(1)-p(2)
　　　 - (3/2)m(2)2-p(1)-p(2)+ (3/2)m(2)2-p(2) - 2-p(2) - n0
= n0{(3/2)m(1)+m(2)2-p(1)-p(2) - 1} + (3/2)m(1)+m(2)2-p(1)-p(2)- (3/2)m(2)2-p(1)-p(2)
　　　+ (3/2)m(2)2-p(2) - 2-p(2)
= n0{(3/2)m(1)+m(2)2-p(1)-p(2) - 1} + (3/2)m(2)2-p(1)-p(2){ (3/2)m(1)- 1} + 2-p(2){(3/2)m(2)- 1}

(3) 同様にして
　　　nm(1)+p(1)+m(2)+p(2)+m(3)+p(3) = q3　, k3 = (q32p(3) + 1)/3m(3)
　　　nm(1)+p(1)+m(2)+p(2) = 2m(3)(q32p(3) + 1)/3m(3) - 1= (q32m(3)+p(3) + 2m(3))/3m(3) - 1
　　　q32p(3) = 3m(3)(nm(1)+p(1)+m(2)+p(2) + 1)/2m(3) - 1 = (nm(1)+p(1)+m(2)+p(2) + 1)(3/2)m(3) - 1

q3= {(nm(1)+p(1)+m(2)+p(2) + 1)(3/2)m(3)2-p(3) - 2-p(3)
= {(n0+1)(3/2)m(1)+m(2)2-p(1)-p(2)
　　　- (3/2)m(2)2-p(1)-p(2) + (3/2)m(2)2-p(2) - 2-p(2) + 1}(3/2)m(3)2-p(3) - 2-p(3)
= (n0+1)(3/2)m(1)+m(2)+m(3)2-p(1)-p(2)-p(3) - (3/2)m(2)+m(3)2-p(1)-p(2)-p(3)
　　　+ (3/2)m(2)+m(3)2-p(2)-p(3) - (3/2)m(3)2-p(2)-p(3)+ (3/2)m(3)2-p(3) - 2-p(3)

　　　3回目の一連の作業が終わって q3 が求められその増減数z3 は

z3 = q3 - q2
= (n0+1)(3/2)m(1)+m(2)+m(3)2-p(1)-p(2)-p(3) - (3/2)m(2)+m(3)2-p(1)-p(2)-p(3)
　　　+ (3/2)m(2)+m(3)2-p(2)-p(3)- (3/2)m(3)2-p(2)-p(3)+ (3/2)m(3)2-p(3) - 2-p(3)
　　　 - {(n0+1)(3/2)m(1)+m(2)2-p(1)-p(2) - (3/2)m(2)2-p(1)-p(2) + (3/2)m(2)2-p(2) - 2-p(2) }
= (n0+1)(3/2)m(1)+m(2)-p(1)-p(2) {(3/2)m(3)2-p(3) -1} - (3/2)m(2)+m(3)2-p(1)-p(2)-p(3)
　　　+ (3/2)m(2)+m(3)2-p(2)-p(3) - (3/2)m(3)2-p(2)-p(3) +(3/2)m(3)2-p(3) - 2-p(3)
　　　+ (3/2)m(2)2-p(1)-p(2) - (3/2)m(2)2-p(2) + 2-p(2)
= (n0+1)(3/2)m(1)+m(2)-p(1)-p(2) {(3/2)m(3)2-p(3) -1} - (3/2)m(2)+m(3)2-p(2)-p(3)(2-p(1)- 1)
　　　+ (3/2)m(2)2-p(2) (2-p(1)- 1) - (3/2)m(3)2-p(3)(2-p(2)- 1) - 2-p(3) + 2-p(2)
= (n0+1)(3/2)m(1)+m(2)-p(1)-p(2) {(3/2)m(3)2-p(3) -1 } + (3/2)m(2)2-p(2){(3/2)m(3)2-p(3)- 1}(1 - 2-p(1))
　　　+ (3/2)m(3)2-p(3)(1 - 2-p(2)) - 2-p(3) + 2-p(2)

　　　最初からの増減数z は

z = q3 - n0
= (n0+1)(3/2)m(1)+m(2)+m(3)2-p(1)-p(2)-p(3) - (3/2)m(2)+m(3)2-p(1)-p(2)-p(3) + (3/2)m(2)+m(3)2-p(2)-p(3)
　　　- (3/2)m(3)2-p(2)-p(3)+ (3/2)m(3)2-p(3) - 2-p(3) - n0
= n0{(3/2)m(1)+m(2)+m(3)2-p(1)-p(2)-p(3) - 1} + (3/2)m(2)+m(3)2-p(1)-p(2)-p(3){(3/2)m(1) - 1}
　　　+ (3/2)m(3)2-p(2)-p(3){ (3/2)m(2)- 1} + 2-p(3){(3/2)m(3)- 1}
= [n0{ 3m(1)+m(2)+m(3)- 2p(1)+p(2)+p(3)+m(1)+m(2)+m(3)} + 3m(2)+m(3){ 3m(1) - 2m(1)}
　　　+ 3m(3)2p(1)+m(1){ 3m(2)- 2m(2)} + 2p(1)+p(2)+m(1)+m(2){ 3m(3)- 2m(3)}]/2p(1)+p(2)+p(3)+m(1)+m(2)+m(3)

(4) 同様にして
　　　nm(1)+p(1)+m(2)+p(2)+m(3)+p(3)+m(4)+p(4) = q4　, k4 = (q42p(4) + 1)/3m(4)
　　　nm(1)+p(1)+m(2)+p(2)+m(3)+p(3) = 2m(4)(q42p(4) + 1)/3m(4) - 1= (q42m(4)+p(4) + 2m(4))/3m(4) - 1

q42p(4) = 3m(4)(nm(1)+p(1)+m(2)+p(2)+m(3)+p(3) + 1)/2m(4) - 1
= (nm(1)+p(1)+m(2)+p(2)+m(3)+p(3) + 1)(3/2)m(4) - 1

q4 = {(nm(1)+p(1)+m(2)+p(2)+m(3)+p(3) + 1)(3/2)m(4)2-p(4) - 2-p(4)
=[(n0+1)(3/2)m(1)+m(2)+m(3)2-p(1)-p(2)-p(3) - (3/2)m(2)+m(3)2-p(1)-p(2)-p(3) + (3/2)m(2)+m(3)2-p(2)-p(3)
　　　- (3/2)m(3)2-p(2)-p(3)+ (3/2)m(3)2-p(3) - 2-p(3)](3/2)m(4)2-p(4)+ (3/2)m(4)2-p(4) - 2-p(4)
= (n0+1)(3/2)m(1)+m(2)+m(3)+m(4)2-p(1)-p(2)-p(3)-p(4) - (3/2)m(2)+m(3)+m(4)2-p(1)-p(2)-p(3)-p(4)
　　　+ (3/2)m(2)+m(3)+m(4)2-p(2)-p(3)-p(4) - (3/2)m(3)+m(4)2-p(2)-p(3)-p(4)+ (3/2)m(3)+m(4)2-p(3)-p(4)
　　　- (3/2)m(4)2-p(3)-p(4)+ (3/2)m(4)2-p(4) - 2-p(4)

　　　4回目の一連の作業が終わって q4 が求められその増減数z4 は

z4 = q4 - q3
= (n0+1)(3/2)m(1)+m(2)+m(3)+m(4)2-p(1)-p(2)-p(3)-p(4) - (3/2)m(2)+m(3)+m(4)2-p(1)-p(2)-p(3)-p(4)
　　　+ (3/2)m(2)+m(3)+m(4)2-p(2)-p(3)-p(4) - (3/2)m(3)+m(4)2-p(2)-p(3)-p(4)+ (3/2)m(3)+m(4)2-p(3)-p(4)
　　　- (3/2)m(4)2-p(3)-p(4)+ (3/2)m(4)2-p(4) - 2-p(4)
　　　- [(n0+1)(3/2)m(1)+m(2)+m(3)2-p(1)-p(2)-p(3)- (3/2)m(2)+m(3)2-p(1)-p(2)-p(3)
　　　+ (3/2)m(2)+m(3)2-p(2)-p(3) - (3/2)m(3)2-p(2)-p(3)+ (3/2)m(3)2-p(3) - 2-p(3)]
= (n0+1)(3/2)m(1)+m(2)+m(3)2-p(1)-p(2)-p(3) {(3/2)m(4)2-p(4)-1}+ (3/2)m(2)+m(3)+m(4)2-p(2)-p(3)-p(4){1-2-p(1)}
　　　+ (3/2)m(3)+m(4)2-p(3)-p(4) {1 - 2-p(2)}+ (3/2)m(4)2-p(4){ 1 - 2-p(3)} - 2-p(4)
　　　- (3/2)m(2)+m(3)2-p(2)-p(3){ 1 - 2-p(1)} - (3/2)m(3)2-p(3){ 1 - 2-p(2)} + 2-p(3)
=(n0+1)(3/2)m(1)+m(2)+m(3)2-p(1)-p(2)-p(3){(3/2)m(4)2-p(4)-1}
　　　+ (3/2)m(2)+m(3)2-p(2)-p(3){(3/2)m(4)2-p(4)- 1}{1-2-p(1)}
　　　+ (3/2)m(3)2-p(3) {(3/2)m(4)2-p(4) - 1}{1 - 2-p(2)}+ (3/2)m(4)2-p(4){ 1 - 2-p(3)} - 2-p(4)+ 2-p(3)

　　　最初からの増減数z は

z = q4 - n0
= (n0+1)(3/2)m(1)+m(2)+m(3)+m(4)2-p(1)-p(2)-p(3)-p(4) - (3/2)m(2)+m(3)+m(4)2-p(1)-p(2)-p(3)-p(4)
　　　+ (3/2)m(2)+m(3)+m(4)2-p(2)-p(3)-p(4) - (3/2)m(3)+m(4)2-p(2)-p(3)-p(4)+ (3/2)m(3)+m(4)2-p(3)-p(4)
　　　- (3/2)m(4)2-p(3)-p(4)+ (3/2)m(4)2-p(4) - 2-p(4) -n0
= n0{(3/2)m(1)+m(2)+m(3)+m(4)2-p(1)-p(2)-p(3)-p(4) - 1}+(3/2)m(2)+m(3)+m(4)2-p(1)-p(2)-p(3)-p(4){(3/2)m(1)- 1}
　　　+ (3/2)m(3)+m(4)2-p(2)-p(3)-p(4){(3/2)m(2)- 1}+ (3/2)m(4)2-p(3)-p(4){(3/2)m(3)- 1}+ 2-p(4){(3/2)m(4) - 1}
= [n0{3m(1)+m(2)+m(3)+m(4)-2p(1)+p(2)+p(3)+p(4)+m(1)+m(2)+m(3)+m(4)}
　　　+ 3m(2)+m(3)+m(4){3m(1)- 2m(1)} + 3m(3)+m(4)2p(1)+m(1){3m(2)- 2m(2)}+ 3m(4)2p(1)+p(2)+m(1)+m(2){3m(3)- 2m(3)}
　　　+ 2p(1)+p(2)+p(3)+m(1)+m(2)+m(3){3m(4) - 2m(4)}]/2p(1)+p(2)+p(3)+p(4)+m(1)+m(2)+m(3)+m(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・


(5) 同様にしてこの作業を n 回繰り返せば
　　　nm(1)+p(1)+m(2)+p(2)+m(3)+p(3)+m(4)+p(4)+・・・+m(n)+p(n) = qn　,
　　　kn = (qn2p(n) + 1)/3m(n)
　　　nm(1)+p(1)+m(2)+p(2)+m(3)+p(3)+・・・+m(n-1)+p(n-1) = 2m(n)(qn2p(n) + 1)/m(n) - 1= (qn2m(n)+p(n) + 2m(n))/3m(n) - 1

qn2p(n) = 3m(n)(nm(1)+p(1)+m(2)+p(2)+m(3)+p(3)+・・・+m(n-1)+p(n-1) + 1)/2m(n) - 1
= (nm(1)+p(1)+m(2)+p(2)+m(3)+p(3)+・・・+m(n-1)+p(n-1) + 1)(3/2)m(n) - 1

qn = { (nm(1)+p(1)+m(2)+p(2)+m(3)+p(3)+・・・+m(n-1)+p(n-1) + 1)(3/2)m(n)2-p(n) - 2-p(n)
= (n0+1)(3/2)m(1)+m(2)+m(3)+m(4)+・・・+m(n)2-p(1)-p(2)-p(3)-p(4)- ・・・-p(n)
　　　- (3/2)m(2)+m(3)+m(4)2-p(1)-p(2)-p(3)-p(4) - (3/2)m(2)+m(3)+m(4)+・・・+p(n)2-p(1)-p(2)-p(3)-p(4)-・・・-p(n)
　　　+ (3/2)m(2)+m(3)+m(4)+・・・+m(n)2-p(2)-p(3)-p(4)-・・・-p(n)
　　　- (3/2)m(3)+m(4)+・・・+m(n)2-p(2)-p(3)-p(4)-・・・-p(n) + (3/2)m(3)+m(4)+・・・+m(n)2-p(3)-p(4)-・・・-p(n)
　　　- (3/2)m(4)+m(5)+・・・+m(n)2-p(3)-p(4)-p(5)-・・・-p(n) + (3/2)m(4)+m(5)+・・・+m(n)2-p(4)-p(5)-・・・-p(n)
　　　　・・・・・・・・・・・・・・・・・・・・・・
　　　- (3/2)m(n)2-p(n-1)-p(n)+ (3/2)m(n)2-p(n) - 2-p(n)

　　　n回目の一連の作業が終わって qn が求められその増減数　zn は

zn = qn - qn-1
= (n0+1)(3/2)m(1)+m(2)+m(3)+・・・+m(n-1)2-p(1)-p(2)-p(3)-・・・-p(n-1){(3/2)m(n)2-p(n)-1}
　　　+ (3/2)m(2)+m(3)+・・・+m(n-1)2-p(2)-p(3)-・・・-p(n-1){(3/2)m(n)2-p(n)- 1}{1 - 2-p(1)}
　　　+ (3/2)m(3)+m(4)+・・・+m(n-1)2-p(3)-p(4)-・・・-p(n-1){(3/2)m(n)2-p(n) - 1}{1 - 2-p(2)}
　　　・・・・・・・・・・・・・・・・・・・・・・・・・
　　　+ (3/2)m(n-1)2p(n-1){(3/2)m(n)2-p(n) - 1}{1 - 2-p(n-2)}
　　　+ (3/2)m(n)2-p(n){ 1 - 2-p(n-1)}
　　　- 2-p(n)+ 2-p(n-1)

　　　最初からの増減数　z は

z = qn - n0
= [n0{3m(1)+m(2)+m(3)+m(4)+・・・+m(n)-2p(1)+p(2)+p(3)+p(4)+・・・+p(n)+m(1)+m(2)+m(3)+m(4)+・・・+m(n)}
　　　+ 3m(2)+m(3)+m(4)+・・・+m(n){3m(1)- 2m(1)}
　　　+ 3m(3)+m(4)+・・・+m(n)2p(1)+m(1){3m(2)- 2m(2)}
　　　+ 3m(4)+・・・+m(n)2p(1)+p(2)+m(1)+m(2){3m(3)- 2m(3)}
　　　 　　 ・・・・・・・・・・・・・・・・・・・・・・・・・
　　　+ 3m(n)2p(1)+p(2)+・・・+p(n-2)+m(1)+m(2)+・・・+m(n-2){3m(n-1)- 2m(n-1)}
　　　+ 302p(1)+p(2)+p(3)+・・・+p(n-1)+m(1)+m(2)+m(3)+・・・+m(n-1){3m(n) - 2m(n)}]
　　　　/2p(1)+p(2)+p(3)+・・・+p(n)+p(4)+m(1)+m(2)+m(3)+m(4)+・・・+m(n)

　　　此処に於いて分子の第１項のn0 の係数となる
　　　{3m(1)+m(2)+m(3)+m(4)+・・・+m(n)-2p(1)+p(2)+p(3)+p(4)+・・・+p(n)+m(1)+m(2)+m(3)+m(4)+・・・+m(n)} は
　　　p(1)+p(2)+p(3)+p(4)+・・・+p(n)　の値が大きくなれば負となりうる。
　　　分子の第２項以降は 3p -2p の形（p ≧ 1）の係数だから全て正となる。
　　　従って z ＜ 0 となるには
　　　3m(1)+m(2)+m(3)+m(4)+・・・+m(n)＜ 2p(1)+p(2)+p(3)+p(4)+・・・+p(n)+m(1)+m(2)+m(3)+m(4)+・・・+m(n)
　　　でなければならない。
　　　 ∴ (3/2)m(1)+m(2)+m(3)+m(4)+・・・+m(n) ＜ 2p(1)+p(2)+p(3)+p(4)+・・・+p(n)
　　　従ってこれら一連の作業を n 回やって上記条件が満たされたとき、
　　　奇数 n0 はそれより小さい q0 に帰着する。




NO.1284 2002.9.17.yokodonある形に表せない整数

模試シリーズ13

p を 2 以上のある整数とする。このとき、

　　　px + y （x , y は整数で、0 ≦ y ≦ x）・・・[＊]

の形に表せる整数について考える。

（1）n ≧ p2 であるような任意の整数 n は [＊] の形に表せることを示せ。

（2）[＊] の形に表せない 0 以上の整数の個数を p で表せ。



NO.1285 2002.9.17.yokodon四面体と平行四辺形

模試シリーズ号外

四面体ＯＡＢＣの辺ＯＡ、辺ＡＢ、辺ＢＣ、辺ＯＣ上に、それぞれ点Ｐ、Ｑ、Ｒ、 Ｓを、以下の条件を満たすように取る。

［ア］ＰＱ//ＯＢ、ＰＳ//ＡＣ

［イ］４点Ｐ、Ｑ、Ｒ、Ｓは同一平面上にある。

（1）四辺形ＰＱＲＳは平行四辺形であることを示せ。

（2）四辺形ＰＱＲＳの面積が最大になるのは、どのような場合か。



NO.1286 2002.9.17.水の流れ等差数列

第１０５回数学的な応募問題

太郎さんは、子供から、次のような問題をもらいました。
ｐ、ｑ（０＜ｐ＜ｑ）を互いに素である自然数とする。 有限個の正の数からなる等差数列で、その項として、 １／ｐ、２／（ｐ＋ｑ）、１／ｑ　を含むものを考える。 そのような数列の中で、和が最小となるものについて、その数列の公差を、ｐ、ｑで表せ。

そこで、太郎さんは、最初、P＝３，ｑ＝５として具体的な数字で考えました。 次に、一般の場合を考えてください。ただし、公差は負の数としておきます



NO.1287 2002.9.18.Junko四角錐台の体積（２）

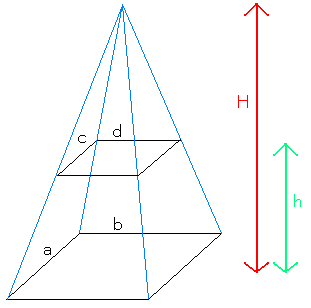
相似の関係をうまく使っていけばいいのではないかと思います。
右図のように四角錐の高さをＨ、四角錐台の高さをｈとします。 相似比の関係から、

　　　ａ：ｃ＝ｂ：ｄ＝Ｈ：Ｈ−ｈ

これより、ａｄ＝ｂｃ・・・(1)、Ｈ＝ａｈ/(ａ−ｃ)・・・(2)

体積　Ｖ＝1/3・ａｂＨー1/3・ｃｄ(Ｈーｈ)
＝1/3・{(ａｂ−ｃｄ)Ｈ＋ｃｄｈ}
＝ｈ/3・{(ａｂ−ｃｄ)・ａ/(ａ−ｃ)＋ｃｄ}　　・・・(2)より

これで、与えられた文字だけを使って体積を表すことができました。
あとは(1)の関係式を使って、よりきれいな式に変形すればいいのかな？

Ｖ＝ｈ/3・{(ａｂ−ｃｄ)・ａ/(ａ−ｃ)＋ｃｄ}
＝1/3・ｈ/(ａ−ｃ)・(ａ2ｂ−ｃ2ｄ)

ｄ＝ｂｃ/ａより、

ａ2ｂ−ｃ2ｄ＝ｂ/ａ・(ａ3−ｃ3) ＝ｂ/ａ・(ａ−ｃ)・(ａ2＋ａｃ＋ｃ2)

Ｖ＝ｈ/3・ｂ/ａ・(ａ2＋ａｃ＋ｃ2)
＝ｈ/3・(ａｂ＋ｂｃ＋２ｂｃ2/ａ)
＝ｈ/6・(２ａｂ＋２ｂｃ＋２ｃｄ)　　　・・・ｂｃ/ａ＝ｄより
＝ｈ/6・(２ａｂ＋ｂｃ＋２ｃｄ＋ａｄ)　　　・・・(1)より　
＝ｈ/6・{(２ａ＋ｃ)ｂ＋(２ｃ＋ａ)ｄ}　






NO.1288 2002.9.1.にゃんこ（二暗刻）コラッツの問題（３）

Ａ-3 以上の検討結果をまとめる

(1) n0 = 1 のとき
　　　n1 = (3n0 + 1)/2 = 4/2 = 2
　　　nm(1) = q12p(1)
　　　∴ m(1) = 1 , p(1) = 1 , q1 = 1
　　　n2 = n1/2 = 1 →　nm(1)+p(1) = q1 に相当する
　　　(3/2)m(1) = (3/2) , 2p(1) = 2
　　　∴(3/2)m(1) ＜ 2p(1) が成り立ち命題は成り立つ。

(2) n0 = 2 のとき
　　　n1 = n0/2 = 1
　　　(1)で　成立することを確認済み

(3) n0 = 3 のとき
　　　n1 = (3n0 + 1)/2 = 10/2 = 5
　　　n2 = (3n1 + 1)/2 = (3・5 + 1)/2 = 8 = 1・23
　　　nm(1) = q12p(1) ∴ m(1) = 2 , p(1) = 3 , q1 = 1
　　　n3 = n2/2 = 4 , n4 = n3/2 = 2 , n5 = n4/2 = 1 , →　nm(1)+p(1) = q1 に相当する
　　　(3/2)m(1) = (3/2)2 , 2p(1) = 23 　　　∴(3/2)m(1) ＜ 2p(1) が成り立ち命題は成り立つ。

(4) n0 = 4 のとき
　　　n1 = n0/2 = 2
　　　(2)で　成立することを確認済み
　　　今後 n0 を順次大きくしていくとすれば n0 が偶数のときは、
　　　それ以前に証明はすまされていることとなるので、以後は省略する。
　　　n0 = k の奇数のときも この命題は成り立つ
　　　何故なら n 回の操作により

z = [k{3m(1)+m(2)+m(3)+m(4)+・・・+m(n)
　　　- 2p(1)+p(2)+p(3)+p(4)+・・・+p(n)+m(1)+m(2)+m(3)+m(4)+・・・+m(n)}
　　　+ 3m(2)+m(3)+m(4)+・・・+m(n){3m(1)- 2m(1)}
　　　+ 3m(3)+m(4)+・・・+m(n)2p(1)+m(1){3m(2)- 2m(2)}
　　　+ 3m(4)+・・・+m(n)2p(1)+p(2)+m(1)+m(2){3m(3)- 2m(3)}
　　　・・・・・・・・・・・・・・・・・・・・・・・・・
　　　+ 3m(n)2p(1)+p(2)+・・・+p(n-2)+m(1)+m(2)+・・・+m(n-2){3m(n-1)- 2m(n-1)}
　　　+ 302p(1)+p(2)+p(3)+・・・+p(n-1)+m(1)+m(2)+m(3)+・・・+m(n-1){3m(n) - 2m(n)}]
　　　　/2p(1)+p(2)+p(3)+・・・+p(n)+p(4)+m(1)+m(2)+m(3)+m(4)+・・・+m(n)

　　　が得られ、分子の第１項の k の係数となる
　　　　　{3m(1)+m(2)+m(3)+m(4)+・・・+m(n)
　　　　　　　　-2p(1)+p(2)+p(3)+p(4)+・・・+p(n)+m(1)+m(2)+m(3)+m(4)+・・・+m(n)} は
　　　p(1)+p(2)+p(3)+p(4)+・・・+p(n)　の値が大きくなれば負となるので
　　　3m(1)+m(2)+m(3)+m(4)+・・・+m(n) ＜ 2p(1)+p(2)+p(3)+p(4)+・・・+p(n)+m(1)+m(2)+m(3)+m(4)+・・・+m(n)
　 ∴ (3/2)m(1)+m(2)+m(3)+m(4)+・・・+m(n)　＜ 2p(1)+p(2)+p(3)+p(4)+・・・+p(n)
　　　となるまで n を増やせば、z ＜ 0 となり、n0 は n0 よりも小さい qn に帰着する。
　　　このようにして n0 はそれより小さい数に帰着していくから、
　　　最終的には 1 → 4 → 2 → 1 を繰り返す　　　Q.E.D.

＜例＞M(n) = (3/2)m(1)+m(2)+m(3)+m(4)+・・・+m(n) , P(n) = 2p(1)+p(2)+p(3)+p(4)+・・・+p(n)

n0 = 5 の場合

nm(n)p(n)qn(3・qn+1)/2の推移 芭(n)廃(n)M(n)zの正負P(n)
0  58      　
1131 131.5−8

n0 = 7 の場合

nm(n)p(n)qn(3・qn+1)/2の推移 芭(n)廃(n)M(n)zの正負P(n)
0  711,17,26       　 　 　
1311320313.375＋2
21258 435.0625−8
31 31 56 7.59375−64

n0 = 27 の場合

nm(n)p(n)qn(3・qn+1)/2の推移 芭(n)廃(n)M(n)zの正負P(n)
0  2741,62     
12131 47,71,107,161,24221 2.25＋2
251121 18272 17.08593＋4
31191 137,20683 25.62890＋8
421103155,233,350104 57.66503＋16
531175 263,395,593,890135 194.6195＋32
641445 668176 985.2612＋64
712167 251,377,566188 1477.891＋256
831283 425,638219 4987.885＋512
921319 479,719,1079,1619, 2429,36442310 11222.74＋1024
1062911 1397,2051,3077,46162912 127834.0＋4096
1143577 8663315 647159.8＋32768
1211433 6503416 970739.7＋65536
1311325 4883517 1456109.61＋131072
141361 923620 2184164.41＋1048576
151223 35,53,803722 3276246.61−4194304
16345 84026 11057332.3−67108864
17131  412916585998.5 −536870912

n0 = 123 の場合

nm(n)p(n)qn(3・qn+1)/2の推移 芭(n)廃(n)M(n)zの正負P(n)
0  123185,278     
121 139209,3142 12.25＋2
221 1572364 25.0625＋4
312 5989,1345 47.59375−16
421 67101,1527 517.08593−32
523 1929,449 838.44335−256
622 1117,2611 1086.49755−1024
721 132013 11194.6195−2048
812 5814 13291.9292−8192
913 1 1516 437.8938−65536









E-mail 戻る