
Weekend Mathematics/コロキウム室/NO.164
| NO.1367 | 2003.3.1. | kirkland | 四面体 |
本年度の京大・理系の問題です。
四面体OABCがあって、OA⊥BC、OB⊥CA、OC⊥ABかつ4面の面積がすべて等しいとき、この四面体OABCは正四面体であることを示せ。
小学生でも解けそうですね。

| NO.1368 | 2003.3.1. | みきちい | 円周率(1) |
「円周率は3.05より大きいことを証明せよ」を教えて下さい。
今年の東大の理系の問題みたいです。昨日の読売新聞に載ってました。

| NO.1369 | 2003.3.2. | Junko | 円周率(2) |
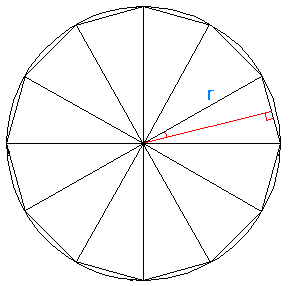
内接正多角形の外周の長さと、円周の長さを比較することで、πの近似値が求められると思います。(右の図は正12角形で内接している様子です。)
円の半径の長さをrとすると、内接正n角形の外周の長さは、
2nr・sin(π/n)
となりますから、円周の長さと比較して、
2nr・sin(π/n)<2πr
つまり、次の不等式を得ます。
n・sin(π/n)<π
半角の公式
sin2θ=(1−cos2θ)/2
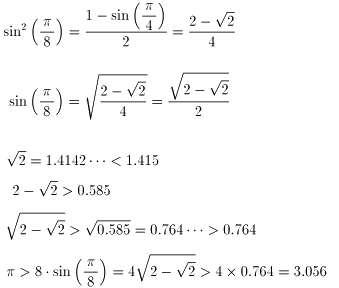
実際の試験会場では電卓を使うことはできないでしょうから、下方の近似でいいとはいうものの根号をはずすのは厳しいかもしれませんね。
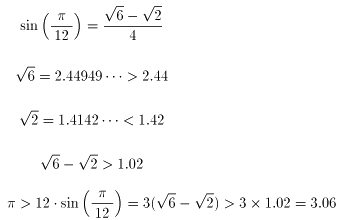
となります。nが大きくなれば当然精度もあがりますから、こちらの方が楽ですね!!

| NO.1370 | 2003.3.3. | 水の流れ | チェビシェフの多項式 |
太郎さんは、奇妙な性質をもつ多項式を応募者の方から教えてもらい、改題して作問をしました。

この問題は 第71回の応募問題「余弦のn倍角」と関連しています。

| NO.1371 | 2003.3.4. | yokodon | 円周率(3) |
1369 では円周の長さと内接する正多角形の周の長さの比較で解決しています
が、他にこんな方針もあるでしょう。一行で書いてしまいます。
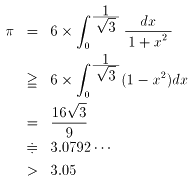
上記の計算の進め方ですが、
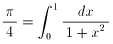
・・・という有名な結果を利用して公比 -x2 の無限等比級数を考えても、題意の主張の成立を示すことが出来ます(有限の部分和を考え、項別積分し、有限和の数値計算をする;ただ、数値計算が、試験の会場ではちょっと大変かも)。
#というより、件の問題を初めて見たとき、僕はこっちを先に思いついたのですが。
##π≒ 3.14 > 3.05 だと、ペケでしょうね(笑)。

| NO.1372 | 2003.3.7. | MagicianKuma | 立方体でないさいころ(1) |
息子から次のような質問をうけて答えられない状態です。
確率を習っているところなんですが、さいころの各面のでる確率は1/6で等しい。
「じゃ、立方体じゃなかったらどうなるの?例えば3cmx4cmx5cmのさいこ
ろだと?」
面積比なのでしょうか?数学の分野?物理の分野?
モデル化はできないのでしょうか?

| NO.1373 | 2003.3.10. | kirkland | 立方体でないさいころ(2) |
| A君 | 「まず、投げ方とか床での跳ね返り方はどのように考えるんですか?よくイカサマ麻雀で『置きサイ』とかするし、 床にめり込んだりしたら大変だし、勢いが強すぎてサイコロが壊れちゃったら困っちゃうし……。」 |
| 先生 | 「相変わらず、細かいねえ。投げ方はともかく、この際、跳ね返り方も無視しよう。要するに、投げたあと床に着地し たら跳ね返らずに、そのまま倒れるという感じでやってみよう。さて突然だが、直方体の重心は、3本の対角線の交 点と一致するんだけど。」 |
| A君 | 「また、獣神サンダーライガーですか?」 |
| 先生 | 「この場合、発泡スチロールでできた直方体のちょうどド真ん中に鉄の玉が埋め込んであるっていうような感じかな。」 |
| A君 | 「何となくイメージできました。発泡スチロールは軽いので重さを無視できて、鉄の玉の重さだけ考えるんですね。」 |
| 先生 | 「そうそう。とりあえずは、横から見た図というか、平面で考えてみよう。投げたあと【図1】のように床に着地する と、その後は、どうなるかは分かるかな?」 |
| A君 | 「簡単っす!長方形IWGPのど真ん中に鉄の玉があるんだから、そのまま真下に落ちてGPが床につきます【図2】。 【図3】のように着地するとWGが床につくんですね。」 |
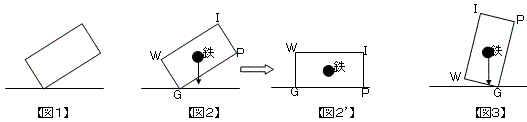
| 先生 | 「その通り。鉄の重さを表す矢印が横切る辺が、床につくわけだが、さりげなくギャグを入れてるんじゃないよ! さて、いちいち長方形を傾けるのは面倒なので、長方形VSOPを固定して、矢印を回すことにしよう。それと、鉄 の玉も省略しよう。例えば、【図4】だと矢印は辺VPを横切っているので、VPが床につくことになる。」 |
| A君 | 「またまた見栄張っちゃって!いつもVOしか飲んでないくせに……。適当な方向に矢印を描いたとき、どの辺を横切 るかで確率が決まるわけですね。それって、辺の長さの比じゃないんですか?」 |
| 先生 | 「【図5】のように、長方形の4頂点を通る円を描くと。」 |
| A君 | 「おおっ納得!中心角に比例するんですね。360°に対する水色の扇形の中心角の割合が、VPが床につく確率です。」 |
| 先生 | 「円周に対する弧VPの長さの割合を考えた方が、あとが楽だ。さて、いよいよ立体的に考えよう。」 |
| A君 | 「例えば、【図6】のように直方体COLTRANEが頂点Nで床に着地したとすると、重さを表す矢印は面LNET を横切るので、この面を下にして倒れます。今度は、矢印が横切る面を考えればいいんですね。2頂点が同時に着地 したときも同じように考えれます。4頂点が同時に着地したときは、言うまでもありませんね。」 |
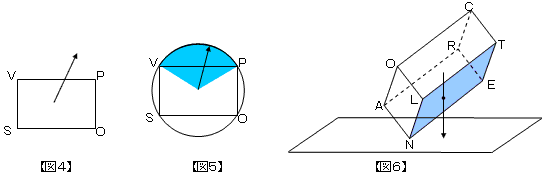
| 先生 | 「分かりにくいギャグを入れるなよ!今度は、直方体ABCD−EFGHのすべての頂点を通る球で考えよう【図7】。 球の中心(これは直方体の重心と一致する)をO、矢印が球の表面と交わる点をPとすると」 |
| A君 | 「例えば、矢印が面ABCDと交わるときに点Pが球の表面を通る部分の面積をSとすると、球の表面積に対するSの 割合=面ABCDが下になる確率っていうことになりますね。でも、点Pは実際どのような範囲を動くんですか?」 |
| 先生 | 「境界だけ考えていこう。【図8】は4頂点C、D、E、Fを通る円を書き加えたものだ。矢印がこの円の弧CDより 上だと面ABCDと交わるし、下だと面CGHDと交わる。よって弧CDは境界の一つだね。」 |
| A君 | 「同じように考えると、4点C、B、E、Hを通る円の弧BCも境界ですね。矢印が弧BCより手前にあると矢印は、 面BFGCと交わってしまいますよね【図9】。しかし、急展開ですね。心なしか、説明も雑なような……。」 |
| 先生 | 「図を描くだけで6時間もかかっているんだから、さすがに疲れたよ。」 |
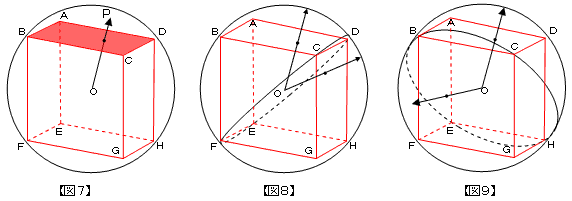
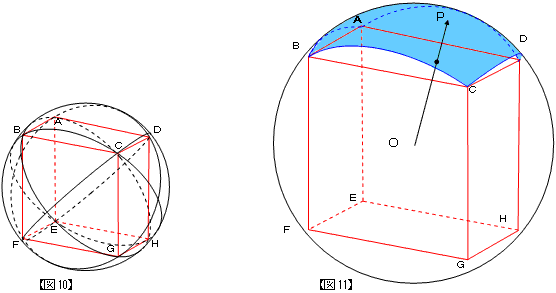
| A君 | 「同様に4点A、B、G、Hを通る円と4点A、D、E、Hを通る円も描き込むと…【図10】。ダメだこりゃ。描いて いる本人ですら分からないや。必要なところだけを描き出すと【図11】の水色の部分が点Pの動く範囲です。とこ ろで先生、この部分の面積ってどうやって求めるんですか?」 |
| 先生 | 「重積分を使えば求められるが、面倒なのでまた今度。」 |
| A君 | 「重責といいつつ無責任、その心は?ところで先生、ずっと疑問に思ってたんですけど、例えば点PがちょうどCに来 たときって、どうなるんですか。1点でバランスを保って、倒れずにいるんですか?今の考え方だと、確率は0になりますが、実際問題うまくいけばそういうこともあり得るんじゃないんですか?」 |
| 先生 | 「それを言い出したら、立方体のサイコロの話もおかしくなってしまうだろ!6分の1じゃなくなってしまうぞ。 そもそも、今回の問題は正直言って自信ないんだよ。重心とか重力とかの考え方がそもそも間違ってるかもしれん。 とにかく物理は分からん!……さようなら。」 |
| A君 | 「あっ、逃げたな!誰か〜まともな考え方を教えてくださ〜い。」 |

| NO.1374 | 2003.3.19. | KAZUTOYO | 積分式の解 |
私は、水産試験場で深層水利用に関する研究を行っています。研究の中で深層水(その中の食塩)の
マグロ肉への浸透速度を測定し、実測値と理論値を比較、評価することとしました。
浸透の理論値を計算する計算式に誤差関数があります。この積分式の解を求めることに苦労しています。
解の求め方、その解を教えていただければ幸いです。
魚肉内の浸透物質の濃度分布
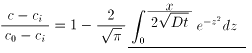
C ・・・魚肉内の食塩濃度
C0 ・・・魚肉表面濃度
Ci ・・・魚肉内の初濃度
x ・・・浸透面(x=0)から浸透方向にとった距離
D ・・・拡散係数
(・・・無次元量)

| NO.1375 | 2003.3.21. | 水の流れ | 絵画鑑賞 |
太郎さんは、以前次のような入試問題を生徒と一緒に考えました。
問題1.
縦1.4mの絵が垂直な壁に掛かっていて、絵の下端が目の高さより1.8m上方の位置にある。
この絵を、縦方向に見込む角が最大となる位置は、壁から何mの所か。
求められた答えが一体どんな数字か知りたくて、文字に置き換えて考えました。
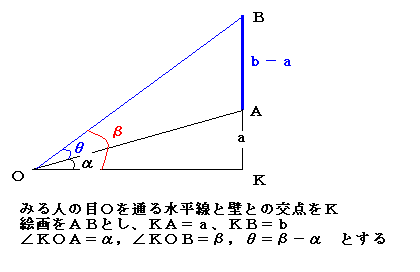
問題2.
縦(b−a)mの絵が垂直な壁に掛かっていて、絵の下端が目の高さよりam上方の位置にある。
この絵を、縦方向に見込む角が最大となる位置は、壁から何mの所か。
ただし、bはaより大きい数とする。また、参考に下のような画像を作ってあります。

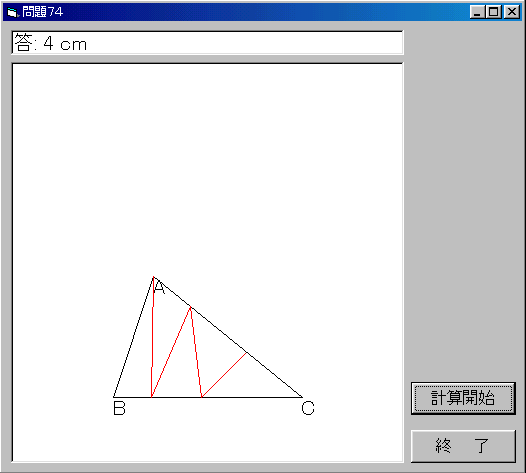
| NO.1376 | 2003.3.21. | 浜田 明巳 | 問題74面積の等しい三角形・その後 |
問題74面積の等しい三角形について、Visual Basic で考えてみました。
Option Explicit
Const BC As Double = 15
Sub Form_Load()
Picture1.BackColor = vbWhite
Picture1.Scale (-8, 26)-(23, -5)
Picture2.BackColor = vbWhite
End Sub
Sub Command1_Click()
Dim Ax As Double, Ay As Double
Dim Bx As Double, By As Double
Dim Cx As Double, Cy As Double
Dim Dx As Double, Dy As Double
Dim Ex As Double, Ey As Double
Dim Fx As Double, Fy As Double
Dim Gx As Double, Gy As Double
Dim Dx_min As Double, Dx_max As Double
Dim Dxx As Double
Dim AE As Double
Dim AE_min As Double, AE_max As Double
Dim AEE As Double
Dim Exx As Double, Eyy As Double
Dim Fx_min As Double, Fx_max As Double
Dim Fxx As Double
Dim EG As Double
Dim EG_min As Double, EG_max As Double
Dim EGG As Double
Dim Gxx As Double, Gyy As Double
Dim AC As Double
Dim EC As Double
Dim a As Double, b As Double, c As Double 'AC:a*x+b*y+c=0
Dim h As Double 'ACを底辺としたときの高さ
Dim dankai As Integer
Dim kizami As Double
Dim min As Double
Dim sa As Double
Dim S As Double '△ABCの五等分
Dim S1 As Double
'
Randomize Timer
Bx = 0: By = 0
Cx = BC: Cy = 0
Ax = Cx * (Rnd * 2 - 0.5): Ay = Cx * Rnd
Dy = 0
AC = Sqr((Cx - Ax) * (Cx - Ax) + (Cy - Ay) * (Cy - Ay))
kizami = (Cx - Bx) * 0.01
S = 0.5 * Cx * Ay * 0.2 '△ABCの五等分
'AC:a*x+b*y+c=0 -> y=(Cy-Ay)/(Cx-Ax)*(x-Ax)+Ay
a = Ay - Cy: b = Cx - Ax: c = Ax * Cy - Cx * Ay
min = 10000
Picture2.Cls
For dankai = 1 To 14 'Dの決定
If dankai = 1 Then
Dx_min = kizami: Dx_max = Cx - kizami
Else
Dx_min = Dxx - kizami: Dx_max = Dxx + kizami
kizami = kizami * 0.1
End If
For Dx = Dx_min To Dx_max Step kizami
S1 = 0.5 * (Dx - Bx) * Ay '△ABD
sa = Abs(S - S1)
If min > sa Then
min = sa
Dxx = Dx
End If
Picture1.Cls
Picture1.Line (Ax, Ay)-(Dxx, Dy), vbGreen
Call ABC(Ax, Ay)
Picture1.Line (Ax, Ay)-(Dx, Dy), vbRed
Next Dx
Next dankai
Dx = Dxx
Picture1.Cls
Call ABC(Ax, Ay)
Picture1.Line (Ax, Ay)-(Dx, Dy), vbRed
'
kizami = AC * 0.01
min = 10000
h = Abs(a * Dx + b * Dy + c) / Sqr(a * a + b * b) 'AEを底辺としたときの高さ
For dankai = 1 To 14 'Eの決定
If dankai = 1 Then
AE_min = kizami: AE_max = AC - kizami
Else
AE_min = AEE - kizami: AE_max = AEE + kizami
kizami = kizami * 0.1
End If
For AE = AE_min To AE_max Step kizami
Ex = ((AC - AE) * Ax + AE * Cx) / (AE + (AC - AE))
Ey = ((AC - AE) * Ay + AE * Cy) / (AE + (AC - AE))
S1 = 0.5 * AE * h '△ADE
sa = Abs(S - S1)
If min > sa Then
min = sa
AEE = AE
Exx = Ex: Eyy = Ey
End If
Picture1.Cls
Picture1.Line (Dx, Dy)-(Exx, Eyy), vbGreen
Call ABC(Ax, Ay)
Picture1.Line (Ax, Ay)-(Dx, Dy), vbRed
Picture1.Line -(Ex, Ey), vbRed
Next AE
Next dankai
Ex = Exx
Ey = Eyy
Picture1.Cls
Call ABC(Ax, Ay)
Picture1.Line (Ax, Ay)-(Dx, Dy), vbRed
Picture1.Line -(Ex, Ey), vbRed
'
kizami = (Cx - Dx) * 0.01
min = 10000
For dankai = 1 To 14 'Fの決定
If dankai = 1 Then
Fx_min = Dx + kizami: Fx_max = Cx - kizami
Else
Fx_min = Fxx - kizami: Fx_max = Fxx + kizami
kizami = kizami * 0.1
End If
For Fx = Fx_min To Fx_max Step kizami
S1 = 0.5 * (Fx - Dx) * Ey '△EDF
sa = Abs(S - S1)
If min > sa Then
min = sa
Fxx = Fx
End If
Picture1.Cls
Picture1.Line (Ex, Ey)-(Fxx, Fy), vbGreen
Call ABC(Ax, Ay)
Picture1.Line (Ax, Ay)-(Dx, Dy), vbRed
Picture1.Line -(Ex, Ey), vbRed
Picture1.Line -(Fx, Fy), vbRed
Next Fx
Next dankai
Fx = Fxx
Picture2.Print "答:"; Fx - Dx; "cm"
Picture1.Cls
Call ABC(Ax, Ay)
Picture1.Line (Ax, Ay)-(Dx, Dy), vbRed
Picture1.Line -(Ex, Ey), vbRed
Picture1.Line -(Fx, Fy), vbRed
'
EC = Sqr((Cx - Ex) * (Cx - Ex) + (Cy - Ey) * (Cy - Ey))
kizami = EC * 0.01
min = 10000
h = Abs(a * Fx + b * Fy + c) / Sqr(a * a + b * b) 'EGを底辺としたときの高さ
For dankai = 1 To 14 'Gの決定
If dankai = 1 Then
EG_min = kizami: EG_max = EC - kizami
Else
EG_min = EGG - kizami: EG_max = EGG + kizami
kizami = kizami * 0.1
End If
For EG = EG_min To EG_max Step kizami
Gx = ((EC - EG) * Ex + EG * Cx) / (EG + (EC - EG))
Gy = ((EC - EG) * Ey + EG * Cy) / (EG + (EC - EG))
S1 = 0.5 * EG * h '△EFG
sa = Abs(S - S1)
If min > sa Then
min = sa
EGG = EG
Gxx = Gx: Gyy = Gy
End If
Picture1.Cls
Picture1.Line (Fx, Fy)-(Gxx, Gyy), vbGreen
Call ABC(Ax, Ay)
Picture1.Line (Ax, Ay)-(Dx, Dy), vbRed
Picture1.Line -(Ex, Ey), vbRed
Picture1.Line -(Fx, Fy), vbRed
Picture1.Line -(Gx, Gy), vbRed
Next EG
Next dankai
Gx = Gxx
Gy = Gyy
Picture1.Cls
Call ABC(Ax, Ay)
Picture1.Line (Ax, Ay)-(Dx, Dy), vbRed
Picture1.Line -(Ex, Ey), vbRed
Picture1.Line -(Fx, Fy), vbRed
Picture1.Line -(Gx, Gy), vbRed
End Sub
Sub Command2_Click()
Unload Me
End Sub
Sub ABC(ByVal Ax As Double, ByVal Ay As Double)
Picture1.Line (Ax, Ay)-(0, 0), vbBlack
Picture1.Line -(BC, 0), vbBlack
Picture1.Line -(Ax, Ay), vbBlack
Picture1.CurrentX = Ax: Picture1.CurrentY = Ay
Picture1.Print "A"
Picture1.CurrentX = 0: Picture1.CurrentY = 0
Picture1.Print "B"
Picture1.CurrentX = BC: Picture1.CurrentY = 0
Picture1.Print "C"
End Sub

 E-mail
E-mail
 戻る
戻る