
Weekend Mathematics/コロキウム室/2000.10〜12/NO.102
| NO.870 | 2000.10.15. | 水の流れ | 約数の最大個数(1) |
太郎さんは、学校で、ある自然数の約数の問題を扱っています。
(ここでは、約数は正の自然数としておきます。)
例えば、36=22×32 と素因数分解できますから、正の約数は、次の表のように表れます。
| 36の約数 | 30=1 | 31=3 | 32=9 |
|---|---|---|---|
| 20=1 | 1 | 3 | 9 |
| 21=2 | 2 | 6 | 18 |
| 22=4 | 4 | 12 | 36 |
また、36の約数の和は、この表の中の9個の和だから、分配法則から、
(1+2+4)×(1+3+9)=91 (答)
ここで、授業中に、生徒に出した問題を書いておきます。
問1:36のこの約数の積を求めよ。
問2:36以下で、36との最大公約数が1である数の個数を求めよ。
問3:36以下で、36との最大公約数が1である数の和を求めよ。
多くの読者の皆さんは、もうこの考え方はよくご存じでしょう。
そこで、新しい疑問を持ち始めました。
1桁の自然数のとき、約数の最大個数は
6=2×3 、8=23 から 4個が最大個数の約数を持ちます。では、
問題4:2桁の自然数のとき、約数の最大個数を持つ自然数を求めよ。
問題5:3桁の自然数のとき、約数の最大個数を持つ自然数を求めよ。
以上から、4桁の場合も出題したいのですが、太郎さんは、まだ答を見いだしていません。

| NO.871 | 2000.10.15. | 水の流れ | 新左衛門の望み(4) |
豊臣秀吉から新左衛門さんの褒美のことを先日書きましたが、実際に計算してみますと、
等比数列の和の公式から、
1+2+4+8+・・・+229=230−1=1、073、741、823粒
になります。
で、昔のこの時代は、お米を年貢として、大名に納めていました。
領地からの年貢米の取り高でその時代の大名の位を決める参考にしていました。
ちなみに、ここ大垣城主戸田藩は10万石と言われています。<BR>
そこで、当時は、穀物(お米等)を測るのに糧の単位が使われていました。
1石(こく)は10斗(とう)、1斗は10升(しょう)、1升は10合(ごう)、
1合は1勺(しゃく)、1勺は10抄(さい)、1抄は10撮(さつ)、1撮は10圭(けい)、
1圭は6粟(ぞく)となっています。
さて、1升は6万粒として計算すると、
新左衛門さんの褒美は一体約何石何斗何升何合何勺くらいになるでしょうか。
皆さん!新左衛門さんは、取り高どの位の家来と同じになったでしょうか。
興味が湧きませんか。
また、今風の尺貫法とメートル法によると、1升は約1.5kgと言われています。

| NO.872 | 2000.10.18. | Junko | 約数の最大個数(2) |
問1
(23・33)3=69=10,077,696
問2
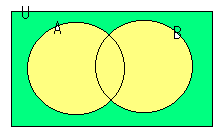
U={x|xは36以下の自然数}
A={x|xは2の倍数、x∈U}
B={x|xは3の倍数、x∈U}とする。
有限集合Xの要素の個数をn(X)とすると、
n(U)=36、n(A)=18、n(B)=12
A∩B={x|xは6の倍数、x∈U}だから、n(A∩B)=6
n(A∪B)=n(A)+n(B)ーn(A∩B)=18+12ー6=24
求めるのは上図のグリーンの部分、n(A∪B)の補集合です。
n(U)−n(A∪B)=36−24=12
問3
有限集合Xの要素の総和をS(X)とすると、
S(U)=1+2+3+・・・36=666
S(A)=2+4+6+・・・36=342
S(B)=3+6+9+・・・36=234
S(A∩B)=6+12+18+・・・36=126
従って上図のグリーンの部分、n(A∪B)の補集合の要素の個数は、
666−(342+234−126)=216
問4
まず素数を小さい方からかけていきます。
2桁の上限が、2×3×5=30です。(更に×7とすると、3桁になってしまう。)
次に指数を上げることを考えます。
22×3×5=60
2×32×5=90の2つで、
約数の個数はともに、3×2×2=12個
一歩戻って、2a×3bタイプなどで(a+1)(b+1)=12を探すと、
23×32=72
25×3=96
問5
3桁も同様に考えます。
まず素数の積は2×3×5×7=210が上限です。(更に×11とすると、4桁になってしまう。)
次に指数を上げることを考えます。
23×3×5×7=840
が約数の個数4×2×2×2=32で最高です。
一歩戻って、2a×3b×5cタイプなどで
(a+1)(b+1)(c+1)=32を探しても見つかりませんので、該当は1つだけとなります。
次は4桁です。
素数の積は2×3×5×7×11=2310が上限です。(更に×13とすると、5桁になってしまう。)
次に指数を上げることを考えます。
23×3×5×7×11=9240
約数の個数は、4×2×2×2×2=64
一歩戻って、2a×3b×5c×7dタイプなので
(a+1)(b+1)(c+1)(d+1)=64を探します。
ありますね。23×33×5×7=7560

| NO.873 | 2000.10.19. | 水の流れ | 約数の最大個数(3) |
問2で、集合の個数から、junko さんは求めておられますが、
この計算をさらに、発展させていきます。
| n(U)−n(A∪B) | |
| = | n(U)−{n(A)+n(B)−n(A∩B)} |
| = | 36−{(36÷2)+(36÷3)−(36÷6)} |
| = | 36(1−1/2−1/3+1/6) |
| = | 36(1−1/2)(1−1/3) |
| = | 36×1/2×2/3 |
| = | 12 ・・・ (答) |
ここで、一般に、自然数Nについて、素因分解をします。
N=ap×bq×cr・・・・とします。
このN以下の自然数でNと互いに素な数の個数はオイラー関数φ(N)といい、
φ(N)=N(1−1/a)(1−1/b)(1−1/c)・・・ と表すことができます。

| NO.874 | 2000.10.21. | 山人 | ビュッフォンの針の実験(6) |
“ビュフォンの針”の問題もエクセルでシュミレーションしてみました。
平行線の間隔 2d=4 したがって d=2
針のながさ 2l=2 したがってl=1 とします。
針の中心から平行線までの距離 x
針と平行線のなす角 θ
0≦x≦2 0≦θ≦π
θが一定のとき針が平行線と交わる確率 x≦sinθ
針が平行線と交わる確率 (sinθの0からπまでの積分)/(2×π)=1/π
したがって π=1/(交わる度数)
乱数を使って x とθを与え、x≦sinθによって交わるかどうかの判定をする。
10000回試行して、交わる度数をカウントすることで、πの近似値を得る。

| NO.875 | 2000.10.22. | 水の流れ | 約数の最大個数(4) |
さて、問3についてですが、別解を投稿します。
36と互いに素な数の和をTとすると
| T | =1+5+7+11+13+17+19+23+25+29+31+35 |
| =(1+35)+(5+31)+(7+29)+(11+25)+(13+23)+(17+19) | |
| =36×6 | |
| =216 |
ここで、一般に、集合Sの中に要素(数)xについて、
数(N−x)もまた、集合Sの中の要素であるとき、
集合Sの中の要素をnとおくと、要素xの総和Tは
T=N×n/2 で求められます。
したがって、オイラー関数オイラー関数φ(N)を用いて、
φ(36)=36(1−1/2)(1−1/3)=12 から
36と互いに素な数の和をTとすると
T=36×φ(36)/2=36×6=216 ・・・ (答)
また、違った角度から見てみると、
| T | =(1+5)+(7+11)+(13+17)+(19+23)+(25+29)+(31+35) |
| =6(1+3+5+7+9+11) ・・・奇数の和の公式から | |
| =6×(62) | |
| =216 |
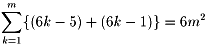

| NO.876 | 2000.10.29. | 水の流れ | 約数と互いに素な数 |
太郎さんは、学校で、ある自然数の約数の問題を扱っています。
(ここでは、約数は正の自然数としておきます。)
例えば、8=23 と素因数分解できますから、正の約数は、1,2,4,8です。
だから、8の約数の個数は 3+1=4 (個)
また、8と互いの素な数は、1,3,5,7の4個です。
これは大変興味深い結果です。正の約数の個数と互いに素な数の個数が一致しています。
勿論、自然数Nについて、N=ap×bq×cr×・・・と素因数分解できたとき、
Nの約数の個数は、 (p+1)(q+1)(r+1)・・・ で求まります。
N以下で、Nと互いに素の数の個数は、オイラー関数φ(N)で表すと、
φ(N)=N(1−1/a)(1−1/b)(1−1/c) ・・・で書けます。
ここで、問題です。自明な1は除いてもいいでしょう。
「自然数Nについて、Nの正の約数の個数と、
N以下でNと互いに素な数の個数とが一致するような自然数Nは
一体どんな数でしょう。」

| NO.877 | 2000.10.29. | Taku | 整数問題 |
a,bを自然数とする。
a2+b2がabで割り切れるための必要十分条件はa=bであることを示せ。

 E-mail
E-mail
 戻る
戻る