
Weekend Mathematics�^�R���L�E�����^NO.161
| NO.1350 | 2003.2.3. | ���̗��� | �O�p�`�̖ʐ�(1) |
���Y����́A���̖��k���玿�₳��܂����B�F����A�l���Ă��������B
���F
���`�a�b�ɂ����āA���_�`����Εӂa�b�ɉ��낵���������`�c�Ƃ��A
�a�c���S�C�b�c���U�C�p�a�`�b���P�R�T���@�Ƃ���B
���̂Ƃ��A�O�p�`�`�a�b�̖ʐς����߂�B

| NO.1351 | 2003.2.3. | Junko | �O�p�`�̖ʐ�(2) |
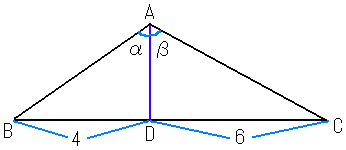
�E�}�̂悤�ɊpABD=���A�pACD=���Ƃ���ƁA��+��=135
AD=x�@�Ƃ���ƁAtan��=4/x�Atan��=6/x
tangent�̉��@�藝
�@�@tan(��+��)=(tan��+tan��)/(1-tan��tan��)
�ɂ��Ă͂߂�ƁAtan135��=-1�@���A
�@�@-1={(4/x)+(6/x)}/{1-(4/x)(6/x)}
������Ax�Q+10x-24=0
x��0���Ax=2
�]���āA�ʐρ@S=10
�����Ƃ������낢�ʉ������肻���ł��ˁB

| NO.1352 | 2003.2.4. | kirkland | �O�p�`�̖ʐ�(3) |
| �`'�N | �u�搶�A���߂܂��āB������̂`�������b�ɂȂ��Ă܂��B�v |
| �搶 | �u���`�A�`�N�̌Z���B�m���A���R��������ˁB���āA�ǂ�����ĉ������̂��ȁH�v |
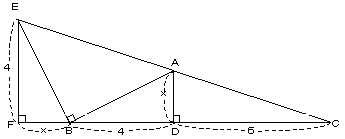
| �`'�N | �u�b�`������Ɂ��`�a�d���a�`���a�d�̒��p�ӎO�p�`�ɂȂ�悤�ɓ_�d���Ƃ�A�d����a�b�ɐ����d�e�����낵 �܂��B���`�a�c�߁��a�d�e�i�ؖ����j�Ȃ̂ŁA�a�c���d�e���S�A�`�c���a�e�i�����Ƃ����j�ł��B ���`�c�b�䁢�d�e�b�Ȃ̂ŁA���F�S���U�F(���{10)�ƂȂ��āA����������ƁA�����O��肘���Q�B ���������āA���`�a�b��10�ł��B�v |
| �搶 | �u�f���炵���B�N�́A���̌��₩�܂����P�זE�Ȓ�Ƃ������ė�V���������A�����L�]���ˁB�v |
| �`'�N | �u���肪�Ƃ��������܂��B���J�ߒ����Č��h�ł��B�v |
| �`�N | �u�N�����₩�܂����ĒP�זE�ł����āH�ӂ���I����Ȗ��A�l�ł������܂���I�v |
| �搶 | �u�����A�����Ă����̂��B��������炸�ڕq���z���B�ł��A����͏��w���ɂ͖��������B ���������A�������i�R���L�E�����j�́A����������ă}�W���Șb���肾���B�N������ƁA�ǂ����b���s�ސT�ɂ� ���č�����ǁB�܂��A�{��ꂿ�Ⴄ��B�v |
| �`�N | �u�搶�ƈ���ď����搶�͊��傾������v�A���v�B���āA�q���g���������B�v |
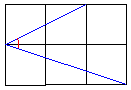
| �搶 | �u���ς�炸�������Ȃ��B�Ƃ肠�����A�q���g�Ƃ��ď����搶�����35�w�R�p�̖��x�ł��ǂ�ł݂�B�v |
| �`�N | �u�ǂ݂܂����B�E�}�̐Ԃ̊p��45���ɂȂ��ł��ˁB���w�Z�ŏK���܂�����B���p�ӎO�p�`���ł����ł��傤�H�v |
| �搶 | �u���̒ʂ�B�܂��A�L���Șb�����珬�w�Z�ŋ����Ă��Ă����������Ȃ��ȁB�v |
| �`�N | �u�Ƃ���Ő搶�A�����̒P�ʂ͂����ł����H���H���[�h�H�͂��܂��A���N�H�v |
| �搶 | �u�����������A���w�����ƒP�ʂ̂Ȃ������͍���B�����ł�����Ȃ��H�v |
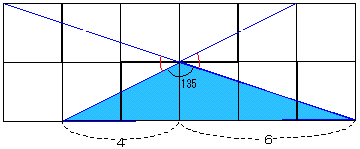
| �`�N | �u�^�����Ă��钷�����U�����ƂS�����Ȃ̂ŁA�@����ɂP�}�X�Q�������ĂƂ���ł��ˁB 135�����Ă����̂́A180���|45���ł��傤�H�a�c�͂Q�}�X������E�E�E �n�j�I�Ђ�߂��܂����I�Q��������Ή��̐}�ł��I���R�ɂ������͂P�}�X���łQ�����B �O�p�`�̖ʐς�10�~�Q���Q��10�����Q�Ł`���B �������A���Ƃ����������ۂ��Ƃ������A�C���`�L�L���Ƃ��������Ƃ������c�c�B �ł��A���܂��݂�A�����Z�M�I�l�ɂ���������`���I�v |
| �`'�N | �u�Ƃ���ł`�B�ꂳ��ɗ��܂�Ă����������A�����ƍs�����̂��H�v |
| �`�N | �u�������A��������Y��Ă��I���Z�l�`�A�ꏏ�Ɏӂ��ĉ�������`�B�v |

| NO.1353 | 2003.2.4. | MagicianKuma | ��`��(12) |
NO.272����n�܂��`��̖��œ����� 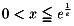 �Ō��_���o�Ă����
���Ȃ̂ł����A
x=-1�@�́@��`��ɓ���Ȃ��̂ł��傤���H�@-1(-1) = -1 , -1^{-1(-1)} = -1 ... ��
y=-1 �ƈ�ӂɌ��܂�܂����H
�Ō��_���o�Ă����
���Ȃ̂ł����A
x=-1�@�́@��`��ɓ���Ȃ��̂ł��傤���H�@-1(-1) = -1 , -1^{-1(-1)} = -1 ... ��
y=-1 �ƈ�ӂɌ��܂�܂����H

| NO.1354 | 2003.2.5. | �c�c�s | �ő��~�����(14) |
*�@���2/12����
�Ƃ肠�����A�Ō�͓����܂����B
�mNO.1344�@�ő��~�����i13�j�̑����n
�t���͍�p���i���L���́C�d�́j�ł̍ő��~���������ײ���܂��B
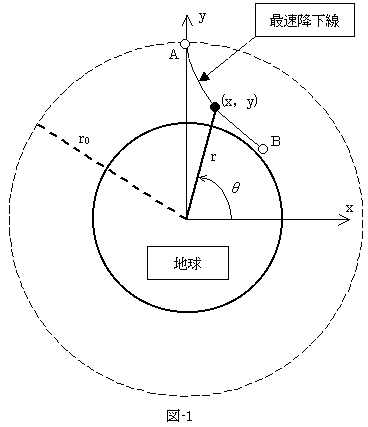
�P�D���̃X�P�b�`
�}-1�̂悤�ɒn���̒��S�Ɍ��_������(x�Cy)���W�n���Ƃ�A���̌��_�𒆐S�Ƃ���ɍ��W�n��(r�C��)�Ƃ��܂��B
�܂��n���̏d�����ݼ�ق́A�ɍ��W�̓��ar��p���āA
�@�@�@�@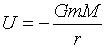 �@�@�@�@�@�@(1)
�@�@�@�@�@�@(1)
�Ə����܂��B������G��ƭ��݂̏d�͒萔�Cm�͍ő��~�������~������_�̎��ʁCM�͒n���̎��ʂł��B��(1)�����ݼ�ق̗�_�́A�������ɂƂ��Ă��܂��B
���ݼ�ق̗�_�͂ǂ��ɂƂ��Ă��ǂ��̂ŁA�}-1�̍ő��~�����̊J�n�_A�̂��锼�ar0�����ݼ�ق̗�_�Ƃ��܂��B��_�����̂悤�ɑI�Ԃ�(1)�́A
�@�@�@�@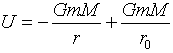 �@�@�@�@�@�@(2)
�@�@�@�@�@�@(2)
�ł��B������r0�|r���̂Ƃ����ƁA
�@�@�@�@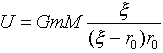 �@�@�@�@�@�@(3)
�@�@�@�@�@�@(3)
�ƂȂ�܂��B�͎̂��_�̗��������ł��B
���_m�̉^���J�n����̌o�ߎ��Ԃ́A���̉^���O���̐��f��ds�Ƃ��āA
�@�@�@�@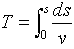 �@�@�@�@�@�@(4)
�@�@�@�@�@�@(4)
�Ōv�Z�ł��܂��B������s�́A�^���J�n�_����m�̌��݈ʒu�܂ł̉^���O���̌ʒ��Cv�͌��݈ʒu�ł̎��_m�̑��x�ŁAv��v(s)�Ƃ������W�͕K���������܂��B��(4)��ds��v���A�ŏ��ɓ�������(x�Cy)���W���A�ɍ��W(r�C��)�ŕ\���A�o�ߎ���T���ŏ��ɂ���E�ӂ̐ϕ��̏����Ƃ��āA���O�����W���������Ɏ������߂܂��B
�Q�D���fds��(r�C��)�\��
�@�@�@�@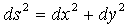 �@�@�@�@�@�@(5)
�@�@�@�@�@�@(5)
�ł����A
�@�@�@�@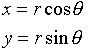 �@�@�@�@�@�@(6)
�@�@�@�@�@�@(6)
�ɒ��ӂ���ƁA
�@�@�@�@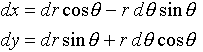 �@�@�@�@�@�@(7)
�@�@�@�@�@�@(7)
�Ȃ̂ŁA
�@�@�@�@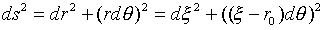 �@�@�@�@�@�@(8)
�@�@�@�@�@�@(8)
�������܂��Bdr�d�Ƃ̍����o�Ȃ��̂́A�����Ȑ����W�̈�ʓI�����ŁA(�́C��)��(r�C��)�Ɠ����ł��邱�Ƃ͖��炩�ł��B
�R�D���xv��(r�C��)�\��
��(3)���A�~�����邱�Ƃɂ���Ď��_m���������A�ʒu�G�l���M�[�̌�����\���܂��B�G�l���M�[�ۑ��������肵�A�^���J�n�_�ł͑��x0�����肷��Ɩ��炩�ɁA
�@�@�@�@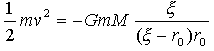
�Ȃ̂ŁA������A
�@�@�@�@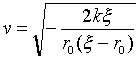 �@�@�@�@�@�@(9)
�@�@�@�@�@�@(9)
�ł��B������GM��k�Ƃ��܂����B��(9)�Ń̂�r0�ɔ�ׂĂ��イ�Ԃ����ꍇ�A����̃̂�����ƁAv��(2GM��/r02)1/2�ł���A�����r0���n���̔��a�Ƒ�̓�������i�n�\�ʕt�߂ł���j�AGM/r02��g�Ȃ̂ŁA�ӂ��̍ő��~�������ɂȂ�܂��B�܂莮(9)����̃̂́A�t���͂Ƃ����������ł͗��Ƃ��Ȃ��킯�ł��B��(8)�C(9)��p����A��(4)�́A
�@�@�@�@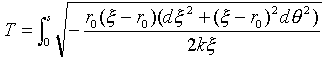 �@�@�@�@�@�@(10)
�@�@�@�@�@�@(10)
�Ə����������܂��B
�S�D�^���O���̓���
��(8)��(9)�͂����Ȃ�A(x�Cy)�n��(r�C��)�n�i��������(�́C��)�n�j�̊Ԃɐ�������2�������W�n�Ԃ̈�ʓI�W�����ɂ����܂���B���������_m�́A�^���O�������킯�ł�����A�̂ƃƂɂ͊��W�́���(��)�ir��r(��)�j�����藧���܂��B�ǂ�Ȋ��`���́A���ꂩ��v�Z����킯�ł����B����Ď�(10)�����̈Ӗ��ɑ����邽�߂ɁAٰē���d��2�Ŋ���Ad��/d�Ƃ�����܂��B�������ȉ��̎�(11)�ɂ����āA�̂͂������Ƃ̊��ƍl���܂��B
�@�@�@�@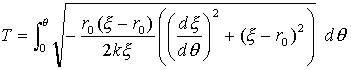 �@�@�@�@�@�@(11)
�@�@�@�@�@�@(11)
���ɐϕ���Ԃ͎�(10)�Łm0�Cs�n�ƂȂ��Ă��܂������A��(11)�ł́A�ϕ����Ұ����Ƃɂ���������Ă���̂ŁAs�ƃƂ̊W���l�����܂��B�}-1���A���_m�����ׂ��ė����ʒ�s�́A���������̂̊��Ƃł������ł��B�̂̓Ƃ̊��ł����Bs��s(��)��s(��(��))�ƂȂ�As���Ƃ̊��Ɖ��肵�܂��B��������Ɛϕ��L����̗Z�ʐ�����A�m0�Cs�n���m0�C�Ɓn�ɏ��������邾���ōς݂܂��B��������ײ��Ư���݁E���ǰ��ł��B�Z�ʂ������Ĉ̂��I�iƭ��݂��Ƃ����͂����Ȃ��C������j�B���Ƃ͎�(11)����ݼޭ�������ɍڂ��邾���ł����A����ǂ����ł��B
�T�D���O�����W���������̌v�Z
��(12)�����O�����W���������ł��B
�@�@�@�@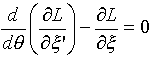 �@�@�@�@�@�@(12)
�@�@�@�@�@�@(12)
�㎮��L�́A�p��𗬗p���ă��O���W�A���ƌĂт܂��B�܂�L�́A��(11)�̐ϕ��L���̒��g�ł��B
�@�@�@�@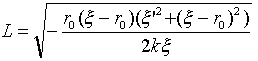 �@�@�@�@�@�@(13)
�@�@�@�@�@�@(13)
�������A
�@�@�@�@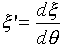
�Ƃ����Ă܂��B��(13)�Ɏ�(12)��������ƁA�t���͉��̍ő��~�����̔������������A
�@�@�@�@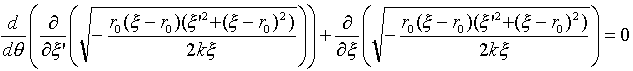 �@�@�@�@�@�@(14)
�@�@�@�@�@�@(14)
�Ɠ����܂����A�x�^�Ȍv�Z������ƁA�ǂ��炢���ɂȂ�܂��B
�U�D�ߎ�������
��(14)�Ń́^r0�`0�����肷��A�Q�D�ŏq�ׂ��悤�ɁA�ʏ�̍ő��~�����ɂȂ肻���ł����A�ʏ�����߂�(x�Cy)�n�ł̔����������ł��B��(14)�́A�ɍ��W(r�C��)�ɓ�����(�́C��)�Ɋւ�����̂Ȃ̂ŁA���̉e���ׂ܂��B���̂��߂Ɏ�(14)��r02�Ŋ���A���̃��O���W�A���́A
�@�@�@�@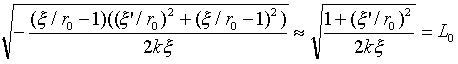 �@�@�@�@�@�@(15)
�@�@�@�@�@�@(15)
�ƂȂ�܂��BL0�́AL�̋ߎ����O���W�A���ł��B����A�ʏ�̍ő��~�����̃��O���W�A���́A
�@�@�@�@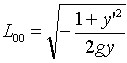 �@�@�@�@�@�@(16)
�@�@�@�@�@�@(16)
�Ə����܂��By'�͂������Ay'��dy/dx�̂��Ƃł��B��(16)��ٰē��Ɂ|�������̂́A�Ⴆ��No.1150�Ȃǂ�y�̕������t������ł��B��(15)��(16)���r����ƁA
�@�@�@�@y �� �|�́Cy' �� �|��'/r0�Cg �� k (17)
�Ƃ����Ή������藧���A�d�͉����x��g����k�ɕύX���ꂽ�ʏ�̍ő��~�����ɂȂ肻���ł����A���̑Ή��́A���͕s���S�ł��B�Ƃ����͎̂�(16)��y'�Ƃ�y'��dy/dx�̂��Ƃł���A��(15)�̃�'�Ƃ̓�'��d��/d�Ƃ̂��ƂȂ̂ŁA(17)�̑Ή������S�ɐ��藧���߂ɂ́Adx�`�|r0�d�Ƃ��K�v�ł��B�����Ŏ�(7)��r��r0�Ƃ����i�́^r0�`0�̉���j�Adx���|r0�d�Ƃ�v������ƃƁ���/2�������A���̂Ƃ�dx���|r0�d�ƁCdy��dr���|d�̂ƂȂ���(17)���������܂��B����āA�}-1�̉^���J�n�_A�̂��イ�Ԃ�ߖT�i���������ɂ��C���������ɂ��j�ł́A�ʏ�̍ő��~�����ŋߎ��ł��܂��B�t���͉͂�]�Ώ̂ȗ͏�Ȃ̂ŁA���̌��ʂ�A�_���n�����̂ǂ��ɂ����Ă������ł��B
�U�D�Ǐ���
�U�D�ł̓́^r0�`0�̉���̂��ƂɁA�ʏ�̍ő��~�����������邽�߂ɂ́Adx���|r0�d�Ƃ��K�v�ł����B����Ȃ炢�����̂��ƁA�ԁ��|r0�ƂȂ���W�n�Ɉڂ��Ă��܂�����ǂ��ł��傤�H�BNO.1150��y���������킹�邱�Ƃɂ���AL00��ٰē��́|�������A��'��d��/d�ԁ��|r0-1�d��/d�Ƃ̂��ƂȂ̂ŁA���x�͎�(15)��(16)�̑Ή������S�ɐ��藧���܂��B
���O�����W��������(12)�́A�ǂ̂悤�ȍ��W�n�Ɉڂ��Ă����藧���Ȃ̂ŁA�́^r0�`0�����̏ꍇ�i���Ȃ킿�������������イ�Ԃ����Ƃ�������݂̂̏ꍇ�j�ɂ��A(�́C��)�n�ł́A�ʏ�̍ő��~�����̌`�������邱�ƂɂȂ�܂��B���̌��ʂ͂�����Ƃт����肵�܂������A(�́C��)�n�Ƃ͐}-2�̂悤�ȍ��W�n�ł��B
(�́C��)���g���������l����킩��悤�ɁA�������������イ�Ԃ����d�͒萔�����Ƃ݂Ȃ���A�n�����S�������Ă���t���͂́A(�́C��)�n�ɂƂ��ẮA(x�Cy)�n�ɂ�����ӂ��̈�l�d�͏�Ɠ����ł��B����Ă���́A�t���͂���]�Ώ̂ȏ�ł���Ƃ�����ʓI��������A�n�ɍŏ��������Ă������������̂ł��B�����ŋɍ��W���g�p�������Ƃ́A�v�Z�Z�p�I�ɂ͖{���I�ł����A�����I�ɂ͖{���I�ł͂���܂���B�ɍ��W�́A�t���͂���]�Ώ̂ȏ�Ȃ̂ŁA����ɍ��킹�����������\����i�ɂ����܂���B���ꂪ�����Ȑ����W���������߂ɁA(x�Cy)�n�ɂ�����ʏ�̖��Ɗ��S�ȑΉ����A���܂��ܗz�Ɏ������Ƃ����̂́A�����Ă��܂��K�^�������Ƃ����킯�ł��B
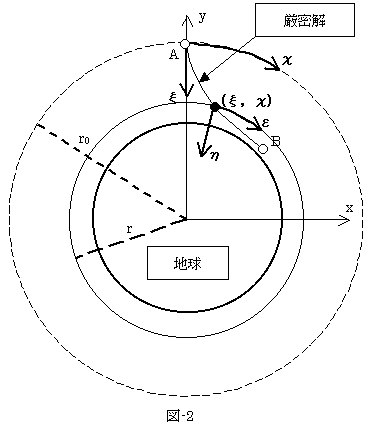
�ȏ�̋c�_�́A�ʂɉ^���J�n��A�_�łȂ��Ă��ł���͂��ŁA�t���͉��ő��~�����̌������̔C�ӂ̈�_�ŁA���̋Ǐ����́A�ʏ�̍ő��~�����̌`�œ����܂��B
�Ǐ�����������A������Ȃ��Ă������Ƃɂ���Č��������A���Ȃ��Ƃ����l�v�Z�I�ɂ͓����܂��B��͓I�Ȍ������͂���̗��z���ł��B�Ǐ����̐ڑ�����͓I�ɍs�������ŁA�������̉\�����������Ă݂܂��B
�܂��Ǐ��������߂܂��B���̂��߂Ɍ������̈�_(�́C��)�̋ߖT�ɁA(�́C��)�n�ɕ��s��(�ŁC��)�n�����܂��B(�ŁC��)�n��(�́C��)�̋ߖT�Ɍ��肳���̂ŁA(�ŁC��)�ł͕��ʂ̍ő��~�������ł��B������Ⴄ�̂́A���_���_(�́C��)�ŏ����x�������Ƃł��B�_(�́C��)�Ŏ��_�������x�́A��(9)�ł��B(�́C��)���炳��Ƀō~��������Ԃ���(9)�őz�����ANO.1150���Q�Ƃ��A(�ŁC��)�n�ł̋Ǐ����̔����������������ƁA
�@�@�@�@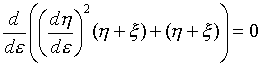 �@�@�@�@�@�@(18)
�@�@�@�@�@�@(18)
�ƂȂ�܂��B�ÂŐϕ����Đϕ��萔��A2�A�Ł{�́�A2sin2(��/2)�Ƃ����ƁA
�@�@�@�@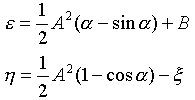 �@�@�@�@�@�@(19)
�@�@�@�@�@�@(19)
�������܂��BA��B�͐ϕ��萔�ŁA�_(�́C��)�ɂ����郿�̏����l����u�ŁA(�ŁC��)��(0�C0)�Ƃ���������������t�����܂��B����͋Ǐ���(19)���A�������̈�_(�́C��)��ʂ�Ƃ��������ł��B
�@�@�@�@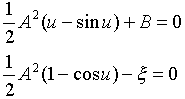 �@�@�@�@�@�@(20)
�@�@�@�@�@�@(20)
���A
�@�@�@�@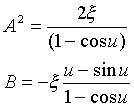 �@�@�@�@�@�@(21)
�@�@�@�@�@�@(21)
������A
�@�@�@�@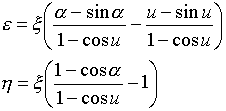 �@�@�@�@�@�@(22)
�@�@�@�@�@�@(22)
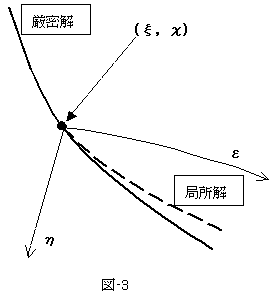
�������܂��B�ϕ��萔��A�CB�Ɠ�������̂ŁA������������K�v�ł��iu�̌���Ɠ����j�B�� �� u�̋Ɍ��ł́A�Ǐ���(22)�͌������Ɛڂ����Ȃ���Ȃ�܂���B�ǂ����Ă��Ƃ����ƁA�������ƋǏ����Ƃ��}-3�̂悤�ȊW�ɂȂ��Ă��Ȃ���A�Ǐ������Ȃ��Č������邱�Ƃ��ł��Ȃ�����ł��B��(22)���A
�@�@�@�@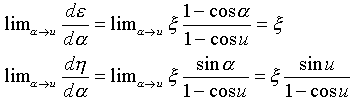
�ł���A�}-3�̏�Ԃ�v������A�� �� u �̋Ɍ��ł́A
�@�@�@�@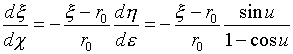 �@�@�@�@�@�@(23)
�@�@�@�@�@�@(23)
���K�v�ł��B��(23)�ł́A
�@�@�@�@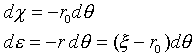
�̊W���g���Ă��܂��BBR>
�́���(��)����(��(�|r0��))�́A�����ȃ��O�����W��������(14)�������̂łȂ���Ȃ�܂���B�����́���(��)�̊��W���킩���Ă���A��(23)����u������ł��܂����A�������́���(��)�����߂����̂ł��B��(23)�͌������i�����j��u�Ƃ̊W�������܂��B�܂�u�́Au��u(�́C��)�ł���(�ŁC��)�n�̌��_(�́C��)���ƂɈႤ���̂��Ƃ������Ƃł��B�Ƃ������Ƃ͐��l�ϕ����s�����Ƃ������l���Ă݂Ă��A�����Ɗ֘A�t����ꂽu�̌�����������K�v�ł��B���̂��Ƃ͗�Âɍl���Ă݂�A���͓��R�̂��Ƃł��B
�����ȃ��O�����W��������(14)�́A2�K�̔����������ł��B�ϕ��萔�͓����A����͌����ȍő��~�������ʉ߂���n�_�ƏI�_���猈�܂�܂��B������Ǐ����̎n�_�ƏI�_�����߂�A��B�܂��́AA��u�ɂ��������Ă݂�A�Ǐ����̎n�_�ƏI�_�͌������̓�_��ʉ߂��Ȃ���Ȃ�Ȃ��̂ŁA�Ђ��Ă͌������̎n�_�ƏI�_�Ƃ̊W�ɂ���Č��肳��A�������i�����j�Ƃ̊W�͔����Ēʂ�Ȃ����ƂɂȂ�܂��B�������̔������������K�v�ł��B
�����ȃ��O�����W��������(14)�́A�ǂ��炢���ɂȂ肻���Ȃ̂ŗ��Ԃ��܂��B���𗠕Ԃ��̂��Ƃ����ƁA��(14)�ł́A�̂̓Ƃ̊��ƍl���Ă��܂����i���ꂪ�ł����S�ł��j�B�������Ƃ��̂̊��ƍl���Ă͂����Ȃ��ł��傤���H�B
�܂����邳������Ȃ���A����͏�ɂł��܂��i���Ȃ����A�����v�������̂ł��j�B���ɕ����I�Ƃ��āu�ő��~�����v�Ȃ̂ŁA�̂ƃƁi�܂��̓ԁj�́A1��1�ɑΉ��������ł��B�Ƃǂ߂Ƃ��ẮA�������肵�Čv�Z���āA���ʂ�����ɍ������������̘b�ł��B���������킯�ŁA�Ƃ��̂̊��Ƃ݂Ȃ��܂��B��(10)�ɖ߂�܂��傤�B��(10)���ċL������(24)�ɂ����āA�Ƃ��̂̊��Ƃ݂Ȃ��܂��B
�@�@�@�@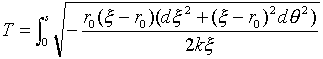 �@�@�@�@(24)
�@�@�@�@(24)
�Ƃ��̂̊��̊��Ƃ݂Ȃ����̂�����Aٰē���d��2�Ŋ���ׂ��ł��B��'��d��/d�̂Ƃ��āA
�@�@�@�@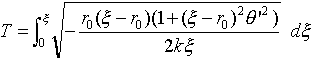 �@�@�@�@(25)
�@�@�@�@(25)
�ƂȂ�܂��B���O���W�A���͎���(26)�ƂȂ�A���܂�(13)�ƕς�����悤�ɂ݂͂��܂���B
�@�@�@�@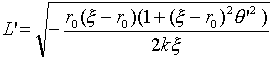 �@�@�@�@(26)
�@�@�@�@(26)
���������O�����W��������������ƁA���ʂ������킩��܂��B���O�����W���������́A�ǂ̂悤�ȕϐ��ϊ����s�����Ɛ��藧���ł����B��(14)��(�́C��)����(�ƁC��)�Ɉڂ낤�Ƃ������ł��B
�@�@�@�@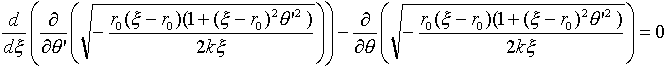 �@�@�@�@(27)
�@�@�@�@(27)
��(27)��2���ڂɒ��ڂ���ƁA���O���W�A���̓Ƃ�z�Ɋ܂݂܂���B�]���āA
�@�@�@�@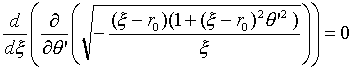
�Ƃ����AC��ϕ��萔�Ƃ��āA
�@�@�@�@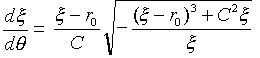 �@�@�@�@(28)*
�@�@�@�@(28)*
�ƂȂ�܂��B*������C��0�ŁA�}-1���Ad��/d�Ɓ�0�Ƃ��܂����B
��(28)������������Ƃ��Đϕ��ł���A�̂ƃƂ̗z�ȊW��^������͂��ł����A�l�͂�����߂܂����B�ł������Ȃ�ƁA���l�������߂邵������܂���B���̂��߂ɁA���l�ϕ��ɕ֗��ȑ��I�Ȕ������������܂��B
�W�D���I�Ȑ��l��
�܂��ԂƃƂ̊W�́Ad�ԁ��|r0d�ƂȂ̂ŁA
�@�@�@�@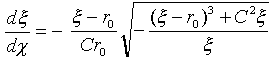 �@�@�@�@(29)*
�@�@�@�@(29)*
�ł��B��(29)����(23)�Ɏg���A
�@�@�@�@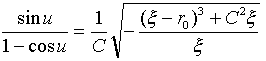 �@�@�@�@(30)*
�@�@�@�@(30)*
�������܂��B���(�ŁC��)�n�͈�_(�́C��)�̋ߖT�n�Ȃ̂ŁA��(22)����������̂́Ad�������|u���������͈͂Ɍ����܂��B�����d�Á��|r�d�ƁCd�Ł�d�̂ɒ��ӂ��āA��(22)�����Ŕ�������A
�@�@�@�@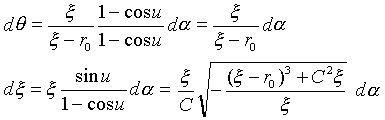 �@�@�@�@(31)*
�@�@�@�@(31)*
�������܂��B��(31)�̍��ӂ́A�������̑��ϐ��̔���(d�́Cd��)�ł���A�E�ӂ�d���̌W�������ϐ��݂̂̂ŕ\�킳��Ă���̂ŁA���͂�p�����[�^���͋Ǐ����̃p�����[�^�Ƃ��Ăł͂Ȃ��A���I�ȃp�����[�^�ƍl���đ��v�ł��B
����ĉ^���J�n�_�̍��W(��0�C��0)�ɁAd���������Ƃ��Ď�(31)���猈�肳���(d�́Cd��)���A�Ђ�������������Ă����A�������̋ߎ����������܂��B���������l�������߂邽�߂ɂ́A�ϕ��萔����̓I�Ɍ��߂�K�v������܂��B�ϕ��萔�����߂܂��B��(31)�ɂ́A�ϕ��萔��3����܂��B���ꂼ��A
�@�@�@ �^���J�n�_�̍��W�ɑΉ�������́D
�@�@�A �^���I���_�̍��W�ɑΉ�������́D
�@�@�B �}��ϐ����̏����l�Ɋւ�����́D
�ƂȂ�܂��B�@�C�B�͎�(31)�̈Ӗ�����Öقɗv������A�A������C�Ƃ��ėz�Ɋ܂܂�܂��B�܂��B�́A�������p�����[�^�ƂȂ����̂ŔC�ӂł��B�^���J�n�_�Ń���0�Ƃ��܂��B�@�ɂ��Ă͐}-1���Q�Ƃ��A�^���J�n�_��(��0�C��0)��(r0�C��/2)�Ƃ��܂��B�A��C�ɂ��Ăł����A��(31)��d�́��̉E�ӂ�ٰē��́A���0�ȏ�łȂ���Ȃ�܂���B���ʒu�݂̂̂̊��ł��B����́A�ۑ��n�ɂ�����L���Ӗ��ł̐U���^����\�킷�����������Ɉ�ʓI�ȏŁA��(31)��ٰē���0�Ƃ���́���1���A�^���̉�A�_��\�킵�܂��B�ǂ����Ă��Ƃ����ƁA�́���1�ł�ٰē������ƂȂ�̂ŁA�́���1����^���𑱂��邽�߂ɂ́A�̂͌�������ق��Ȃ�����ł��B���ہA�́���1�ł͎�(31)��ٰē���0��d�́�0�ł���A����̓̂��ɒl�ɒB�������Ƃ������܂��B����ĉ^���̉�A�_��1���z�����^���́A�n���ۑ��I�ł��邱�Ƃ���A�́���1�Ő��������^�����t�����ɂ��ǂ邱�ƂɂȂ�܂��B*���Ȃ킿��(28)�̃��[�g�̕��������߂�Ƃ��Ɏ̂Ă��A�}�C�i�X�����̕Њ���ɁA���͐ڑ�����邱�ƂɂȂ�܂��B�ȏ�̏́A�Ⴆ�A�P�U���̔����������̑��ϕ��Ɠ����ł��B�����ăƁ���(��)�Ɨ��Ԃ���Ɖ��肵�����Ƃ́A���Ȃ��Ƃ���A�_�܂ł͐������������Ƃ��ۏ���܂��B��A�_�܂ł͐������̂ŁA���Ƃ͉�A�_�ŋ敪���ċ敪�I�ɉ������Ă����Ηǂ����Ƃ��킩��܂��B
��(31)���Aٰē���0�ȏ�ƂȂ邽�߂ɂ́A
�@�@�@�@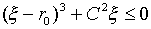 �@�@�@�@(32)
�@�@�@�@(32)
���K�v�ł��B����̃́���1�ŁA��(32)�̓����𐬗�������C��I�Ƃ��A�́���1���ő��~���ł�����E�~�������ɂȂ�܂��B
�X�D�ʏ�̖��Ƃ̑Ή�
��(31)���ڂ������ׂ�A�����ƒʏ�̍ő��~�������Ƃ̑Ή������͂��ł��B���ɏd�͒萔�̕ω��ɂ���āA�T�C�N���C�h�̓]���蔼�a���ǂ̂悤�ɕω�����̂��Ƃ��ׂ���Ǝv���܂��B�ł������A���イ�Ԃ��̂ŁA�܂��̋@��ɁE�E�E�Ƃ������ƂŁE�E�E�����܂����B

| NO.1355 | 2003.2.7. | Hkeisuke | �ő��~�����(15) |
�����[���ǂ܂��Ă��������܂����B�l�Ȃ��s���ŋǏ��������߂邱�ƂȂ�Ďv�������т܂���ł����B�Ō�̂ق��̎����g���Đ��l�������߂Ă݂悤�Ǝv���܂��B�ꉞ�����̂���Ă݂����@�ƍŏI�I�ȖڕW�������Ƃ��܂��B
�l���A�p������ƁA�͂��߂Ƀ��O�����W�A�������߂āA���ꂩ��n�~���g�j�A���܂ō���č�p�ϐ��A�p�ϐ����g���ĉ������Ƃ��܂����B(�ł��r���Œf�O�ł��E�E)
����ŖڕW�Ȃ�ł����A�{���͂����ЂƂV�̂������āA3�̖��ɂȂ����Ƃ��̍ő��~�����𐔒l�v�Z�ł��Ȃ�ł��������猩�Ă݂����̂ł��B�ǂ����ŃX�D�C���O�o�C�̂��Ƃ������Ă����āA����ɂ��ƁA�X�D�C���O�o�C�������Đl�H�q���𑼂̘f���܂Ŕ���ƁA���ʂɍs�����Ƃ����肩�Ȃ葁���s����Ƃ����̂ł��B����ŁA�����ő��~��������������A����͂��̃X�E�B���O�o�C�ɂ��O����ʂ�̂�����Ƃ��P�Ȃ�ʏ�̍ő��~�������Ȃ����悤�ȋO���ɂȂ�̂��B���낢��W���Ă��Ăǂ��Ȃ�̂��킩��܂��A�������l�v�Z���đO�҂̂悤�ȋO�������ꂽ��A�����Ƃ��̂������������邾�낤�Ȃ��E�E�E �Ƃ������ƂŁA�������̂��Ƃɋ��������������������牽�������Ă�������Ɗ������ł��B(����͉����Ȃ���A�Ƃ��ł�)

 E-mail
E-mail
 �߂�
�߂�