
Weekend Mathematics乛僐儘僉僂儉幒乛NO.153
| NO.1289 | 2002.9.19. | BossF | 偁傞宍偵昞偣側偄惍悢乮俀乯 |
(1)
n 亞 p2 偱偁傞偲偒丄n 傪 p偱妱偭偨彜傪 x 梋傝傪 y 偲偡傞偲丄
n = x丒p+y 偱丄
x亞p丄0亝y亝p 偱偡偐傜丄戣堄偼帵偝傟傑偟偨仭
(2)
傑偢丄xi丄yi 偑 * 傪枮偨偟丄xi亙p偺帪
x1亙x2 側傜偽丄
px1+y1亝px1+倶1丂丄 px2亝px2+y2 偱
px2-(px1+倶1)=p(x2-x1)-倶1亞p-x1亜0丂偩偐傜
px1+y1亙px2+y2 偱偁傞乧嘆偙偲偵拲堄偟傑偡丅
偝偰丄 * 偺宍偵昞偣傞偼丄x 傪屌掕偟偰峫偊傞偲
y 偼0乣倶傪摦偔偐傜 x+1 捠傝
傛偭偰丄倶亙倫 偱偺憤悢偼
儼乮倶=0 to p-1)(x+1)=p(p+1)/2
偙傟傜偼丄嘆偵傛傝慡偰堎側傝傑偡偐傜(1)偲偵傛傝
媮傔傞屄悢偼
倫2-1-p(p+1)/2=(p-2)(p+1)/2 乧摎丂丂丂仭

| NO.1290 | 2002.9.19. | BossF | 巐柺懱偲暯峴巐曈宍乮俀乯 |
(1)
堦斒偵2暯柺兛 丄兝 偺岎慄傪 倢 偲偟丄倢 偵暯峴側 兛 忋偺捈慄傪 m 偲偡傞帪丄m傪娷傓暯柺 兞 (亗兛乯偼 l 偵暯峴偱偡偐傜丄兞 偲 兝 偺岎慄 n 偼 倢 偲暯峴偵側傝傑偡丅
偟偨偑偭偰丄PQ//OB//RS, PS//AC//QR乧嘆丂
i.e巐曈宍俹俻俼俽偼暯峴巐曈宍偱偡丅
(2)
傑偢丄嘆傛傝丄
兤=佢QPS=OB偲俙俠偺側偡妏=constant 偵拲堄偟傑偡丅
偝偰丄OP:PA=t:1-t (0亙t亙1) 偲偡傞偲丄
嘆傛傝 PQ=(1-t)OB丄PS=倲AC
傛偭偰
仩PQRS=t(1-t)OB丒AC sin兤/2亝OB丒AC sin兤/8
摍崋偼 t=1/2 偺偲偒
偮傑傝丄P丄Q丄R丄S偑奺曈偺拞揰偱偁傞帪嵟戝偵側傝傑偡丂仭

| NO.1291 | 2002.9.19. | BossF | 摍嵎悢楍乮俀乯 |
傑偢丄桳棟摍嵎悢楍偺岞嵎偼桳棟悢偱偁傞乧嘆偙偲偵拲堄偟傑偡丅
師偵丄1/p,2/(p+q),1/q 偺戝彫傪峫偊傑偡
1/p-2/(p+q)=(q-p)/{p(p+q)}亜0
摨條偵偟偰梕堈偵
2/(p+q)-1/q亜0
偡側傢偪
1/p亜2/(p+q)亜1/q乧嘇
偡傞偲丄榓偑嵟彫偲側傞傕偺傪峫偊傞偺偱偡偐傜
弶崁=1/p 枛崁=1/q 側傞悢楍偱丄崁悢偑嵟傕彮側偄傪峫偊傟偽廫暘偱偡丅乧嘊
偝偰丄嘇傪捠暘偟傑偡偲
{q(p+q)}/{pq(p+q)}亜(2pq)/{pq(p+q)}亜{p(p+q)}/{pq(p+q)}丂偱偡偐傜
1/p,2/(p+q),1/q 偑(偙偺弴偵)摍嵎悢楍偺崁傪側偡
丂丂丂佁q(p+q),2pq,p(p+q) 偑摍嵎悢楍偺崁傪側偡乧嘋
嘋偺帪丄偦偺岞嵎d 偼嘆嘊傛傝惍悢偲偱偒傑偡丅
偝傜偵丄
q(p+q)-2pq=q(q-p)丂2pq-p(p+q)=p(q-p) 偐傜丄
ldl 偼丄q(q-p)丄p(q-p) 偺岞栺悢偱偁傝
崁悢傪嵟彫偵偡傞偨傔偵偼GCM偱偁傞偙偲偑昁梫偱偡
偡側傢偪 ldl=q-p
偡傞偲丄崁悢偼 {q(p+q)-p(p+q)}/ldl=p+q 傛傝 p+q+1崁
埲忋傛傝嵟彫側傞榓偼
(1/p+1/q)(p+q+1)/2 乧摎丂丂丂丂仭

| NO.1292 | 2002.9.21. | wasmath | 偁傞宍偵昞偣側偄惍悢乮俁乯 |
(1)擟堄偺帺慠悢値偵懳偟偰丄
丂丂丂丂倫倶亝値亙倫(倶亄侾)
傪枮偨偡惍悢倶(亞侽)偑懚嵼偡傞丅
値亞倫2側傜偽丄値偺嵟戝惈傛傝
丂丂丂丂倶亞倫
偲側傞偐傜丄
丂丂丂丂倷亖値亅倫倶
偲偍偔偲
丂丂丂丂侽亝倷亙倫(倶亄侾)乕倫倶亖倫亝倶
傛偭偰丄値亖倫倶亄倷丄侽亝倷亝倶偲昞偣傞丅
(2)(1)偺朻摢偱弎傋偨偙偲傛傝丄(*)偺宍偵昞偣側偄侽埲忋偺惍悢偼丄
丂丂丂丂倫倶亄倷(倶亞侽丄倶亄侾亝倷亝倫亅侾)
偲昞偝傟傞偙偲偵側傞丅偙偺傛偆側惍悢偼丄
丂丂丂丂倶亞侽偐偮倶亄侾亝倷亝倫亅侾丄偡側傢偪侽亝倶亝倫亅俀
偺斖埻偵懚嵼偟丄奺倶偵偮偄偰倫亅侾亅倶屄偁傞偐傜丄
媮傔傞屄悢偼丄
丂丂丂丂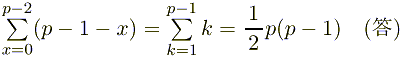

| NO.1293 | 2002.9.23. | 悈偺棳傟 | 夞揮懱偺懱愊乮侾乯 |

| NO.1294 | 2002.9.27. | BossF | 夞揮懱偺懱愊乮2乯 |
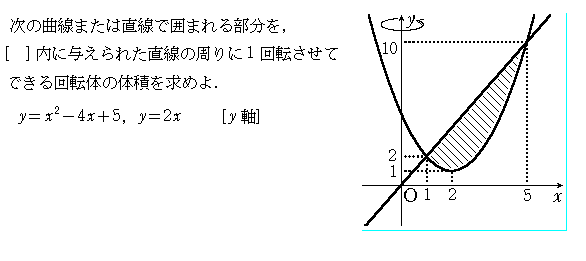
(1) y=x2-4x+5,y=2x [y幉]
y=x2-4x+5傪x偺2師曽掱幃偲尒偰夝偒
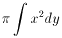
偱丄僑儕僑儕寁嶼偟偰傕偄偄偺偱偡偑乧(^^;;
僶乕儉僋乕僿儞暘妱偲偄傢傟傞搝偱
[夝]
乽x=x 偺帪偺椞堟偺 y 曽岦偺暆偼 -x2+6x-5
偙傟傪倷幉偺夞傝偵夞揮偟偰摼傜傟傞墌摏偺懁柺愊偼
2兾x(-x2+6x-5) 偙傟偵岤傒dx 傪妡偗傟偽
dV= 2兾x(-x2+6x-5)dx 乿(偙傟偼丄摿偵偙偲傢傜側偔偰傕傛偄傛偆偱偡丅)
偟偨偑偭偰
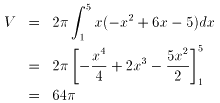 乧摎
乧摎
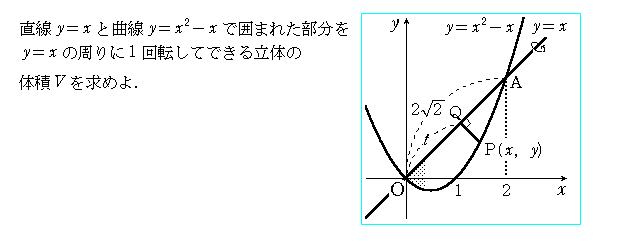
(2)y=x,y=x2-x [y=x]
偙傟傕丄悈偺棳傟偝傫偺僸儞僩偺條偵俹俻傪t偱昞偟偰愊暘偟偰傕偄偄偺偱偡偑乧(^^;;
傂偲偮丄嶱宍暘妱偲偄傢傟傞搝偱
[夝]
乽x=x 偺帪偺椞堟偺 y 曽岦偺暆偼 L=-x2+2x
偙傟傪y=x偺夞傝偵夞揮偟偰摼傜傟傞嶱宍傪峫偊傞丅
嶱宍傪墌悕偺懁柺偲傒偨偲偒丄偦偺墌悕偺掙柺偺敿宎r偼
r=L/併2
偟偨偑偭偰丄嶱宍偺懁柺愊偼兾俴2/併2=兾(-x2+2x)2/併2
偙傟偵岤傒dx傪妡偗偰
dV=兾(-x2+2x)2/併2丒dx=兾/併2丒(x4-4x3+4x2)dx乿
(偙傟傕丄摿偵偙偲傢傜側偔偰偄偄傛偆偱偡丅)
偟偨偑偭偰丄
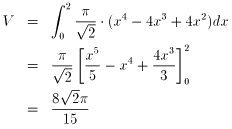 乧摎
乧摎

| NO.1295 | 2002.9.27. | 惏晇 | 倶偺倶忔 |
幙栤側傫偱偡偑倖乮倶乯亖倶倶
傪晄掕愊暘偡傞偲偳偆側傞傫偱偡偐丠

 E-mail
E-mail
 栠傞
栠傞