Weekend Mathematics/コロキウム室/NO.162
コロキウム室
| NO.1356
| 2003.2.12. | DDT | 最速降下問題(16)
|
目標は、スウィングバイ軌道だったんですか。いわれてみればスウィングバイ軌道って、最速降下線ですよね?。軌道の最初は(打ち上げ時は)、最速上昇線かもしれないけど。私も、最速降下線をつなげたような解が出たら、感動します。
スウィングバイ軌道の詳細は知りませんが、ロケットの質量は小さいとして2体問題にするとしても、難しそ~だ~というのが、正直な印象です。たしかスウィングバイのためには、相手の惑星との最適な位置関係も関係してきて、打ち上げのタイミングも重要だったような気がします。ということは、自分と相手の惑星を動かしているのは太陽だから、結局3体問題になるんでしょうか?。でもこれは解析的には解けない。スウィングバイって、ふつうはどう計算されてるのだろう?、そこが知りたいという気持ちになってきます。それにしても、複雑なラグラジアンに対してハミルトニアンまで作ってしまったなんて、それだけですごい!と思います。NO.1354 最速降下問題(14)で明らかなように、私は初っ端で諦めました。
当面の目標は、やっぱりNO.1344 最速降下問題(13)の数値解を出すことです。ところでNO.1354 最速降下問題(14)の式(31)は、
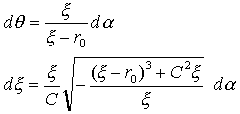 (1)
(1)
となりますが、dαを小さくとって、この式から増分(dξ,dθ)を直接決定して数値積分するのが一番素直です。これは1次のオイラー法といわれるものです。全ての数値積分法の基礎には、この1次オイラー法があり、微分方程式の本質を捉えたものですが、精度が悪いことで知られています。どうしてかというと、現時点(式(1)の右辺)では支配方程式を満たしていますが、現時点からの(ξ,θ)の補外(dξ,dθ)を左辺にとった場合、(dξ,dθ)の正しさは、dαがどれだけ微小かというその一点のみにかかってきて、不用意なdαをとると、あっけなく数値解は発散します。式(1)のように増分(dξ,dθ)を陽に与える数値積分形式を陽解法といって、解の不安定性は陽解法一般の宿命です。例えば陽解法の代表格、4次のルンゲ・クッタ法は非常に巧妙に補外誤差を相殺する式ですが、無限のステップを考えると解はいずれ発散するか、0へ縮退します。しかも解の長持ち程度はdαの大きさに線形にではなく、小さければ小さいほどより長持ちします。よって所定の積分長さの終端で所定の精度で解を得るためには、とんでもないステップ数になる可能性があります。
それに対して陰解法は、(1)のような式を現時点で与えるのは同じですが、増分(dξ,dθ)を、現時点と次のステップとの間の補間問題と考え、できるだけ支配方程式に沿った補間となるように増分(dξ,dθ)をコントロールします。今度も余り大きなdαをとると解が発散し兼ねないのは、数値積分である限り同じですが、解の安定性はずっと良くなります。逆にいうと陰解法では一般に、数値減衰を知らずに導入しています。実際、陰解法の代表格であるニューマークのβ法やウィルソンのθ法では、適当な条件設定を選ぶと解は無条件安定となり、dα=∞の時でさえ解が出て、その解は静的解(つまり動かない)となります。数値減衰を入れすぎたわけです。しかし解の発散傾向と丁度釣り合うだけの増分コントロールを行うと、常にエネルギー保存則を満たすような条件設定も可能です(これがまた微妙なんですけど・・・)。陰解法の欠点としては、増分コントロールのために、各ステップごとに近似的にでも支配方程式を解きなおす必要のあることです。数値積分である限りdαは余り大きくとれません。そうでないと陰解法で数値は出ても(発散しなくても)、答えを信用できないからです。よって積分ステップごとに毎回発生する支配方程式の解きなおしの量が、とんでもない手間になる可能性があります。陰解法のもう一つの欠点は、衝撃問題などで高周波成分が卓越する場合、解が滑らかすぎて使えないという傾向もあります。もっとも高周波成分に敏感な陽解法が収束するくらいに小さいdαを使えばいいわけですが、それなら最初からステップごとには手のかからない陽解法を選びます。よって次のような、都合の良い陽解法が理想です。
陽解法なのに、解の安定性が保証されるもの.
こんな夢のような陽解法なんかありそうもないですが、エネルギー保存則の成り立つ保存系に限れば、じつは存在します。それがシンプレティック積分法といわれる数値積分法です。本当にプロの人達は、必要とあらば、なんでも考え出すものです。で、こういう話題の聞けるところに最近いないのですが、シンプレティック積分法は、いまやもう常識なんでしょうか?。仕事関係の最新版の本や話題を聞いても、どうもそうでない気がします。どなたか教えて下されば幸いです。
シンプレティック積分法も式(1)のような、現時点での陽形式を採用するのですが、そこから増分を補外する補外法のアルゴリズムそのものに、エネルギー保存則が組み込まれます。これは適当な条件設定のもとでの陰解法が、エネルギー保存則を満たすこととは本質的に違います。イメージ図を描けば、ニューマークのβ法では、
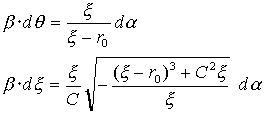 (2)
(2)
のように増分の調節パラメータβを導入し、このβを適当に定めることによって、支配方程式の近似式が満足されるように調整します。エネルギー保存則が満たされるのは、特定のβの値に依存します。いってしまえば補間アルゴリズム自身にとっては、βの値によって、たまたまエネルギー保存則が満たされるだけで、エネルギー保存則と補間アルゴリズム自体とには、本質的には関係がありません。ほとんど全ての数値計算の指導原理は次の一点に尽きると思えます。
じゅうぶん局所的に見れば、どんな関数も線形近似できる.
これが唯一つの指導原理だとすれば、ふつうの数値積分法がエネルギー保存則などと無関係なのは、当然です。つまりアルゴリズム自体が、数値的な積分誤差を緩和してくれるなどということは、期待するほうがどうかしています。ということは、特定のβの値によって厳密にエネルギー保存則を満たすように条件設定してやっても、そうやって生まれる来る解は、外乱に非常に弱い解です。これはβの設定は非常に微妙だと言ってるのと同じです。
βの理論値はもちろん計算できます。しかし理論値を採用しても数値計算には、数値の打切り誤差とまるめ誤差がつきものです(これが外乱です)。何千ステップという積分計算の過程で、その誤差が積もり積もって、エネルギー保存則が厳密に成立するはずがそうでなくなり、解が暴走することさえあります。従って、系の性質をおもんぱかって、理論値に近いが理論値とちょっとだけ違う誤差を貯めないβの値は?、というケースバイケースのトライアンドエラーに陥ります(俗に「はまったよ~~」という状態です)。そして出てきた数値解にどれ程の信用がおけるかは、βを定めた解析者が、問題の系の性質をどれだけ知っているか?、そいつは数値解析の常識を知った奴なのか?とか、結局解析担当者の腕頼みです。だって正解は誰も知りません。解析解が不可能だからこそ数値積分します。
シンプレティック積分法の補外アルゴリズムは、アルゴリズム自体がエネルギー保存則に沿って定式化されます.
なので、エネルギー保存則の成立は偶然ではありません。いいかえれば、少々いい加減な(ξ,θ)と大き目のdαを与えてやっても、アルゴリズム自体が解を軌道修正してくれるために、解はエネルギー曲線のまわりを少しふらつくだけで、めったに発散せず、しかも答えは非常に信用できる、という事態になります。
式(1)で表わされる最速降下線上をすべる質点の運動に対して、このシンプレティック積分法を使おうかと考えています。じつは今まで一回も具体的に計算したことはありません。理論のほうも全然わかってません。
というのはシンプレティック積分法のシンプレティックは、力学系の理論のハミルトン系のシンプレティック形式から来ていて、ここにはいつも多様体による定式化が絡んできて挫折したままだからです。現在なんとか使えそうだと思うのは、数理科学の記事に載っていた、1次のシンプレティック積分だけです。これは実際、1次のオイラー法と同じくらい簡単に見えます。
もし何らかの結果が出れば、お知らせします(またJunko先生にご迷惑をかけることになりますが)。それと、シンプレティック積分法について何かご存知のかたがいらっしゃいましたら、お手数ですが参考文献なり論文なりを教えて頂けないでしょうか?。
- できれば、論文は日本語をお願いします(← 勝手なお願いですが)。
- できれば、シンプレティック積分法をここで解説してください(← もっと勝手なお願いですが)。
[参考文献]
数理科学1995年6月号,特集 古典力学の輝き,サイエンス社

| NO.1357
| 2003.2.14. | 本多欣亮 | Bezier曲線の問題(8)
|
昔投稿した
「Bezier曲線の問題(オフセットしたベジェ曲線の座標を求める計算方法)」ですが、今日すばらしい資料が見つかったよ:
私家版BEZIER講座(pdf)
未解決な部分もあるようだけど、かなり参考になります!

| NO.1358
| 2003.2.16. | 水の流れ | 垂足三角形(1)
|
第114回数学的な応募問題
太郎さんは、2月1日に名城大学の薬学部を受験した生徒から、次のような問題をもらいました。
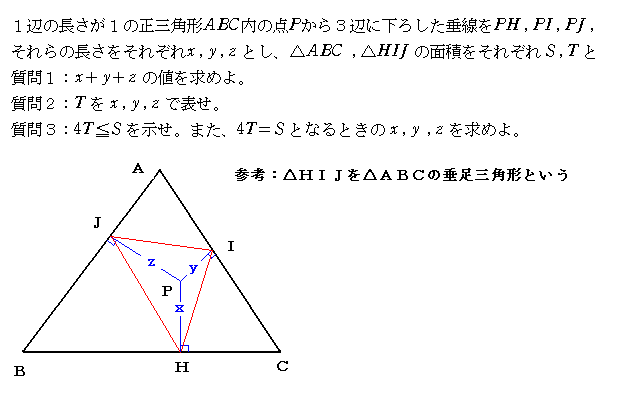
この問題は 第108回の応募問題「最大・最小となる点」と類似していると連想しました。

| NO.1359
| 2003.2.17. | yokodon | 垂足三角形(2)
|
(1)AB=BC=CA= 1 と△ABCの面積が √3/4(=S)であること、
及び△ABC=△APB+△BPC+△CPAであることを用いて、
√3/4 = 1/2・x + 1/2・y + 1/2・z
従って、以下を得ます。
x + y + z = √3/2 …(答)
(2)□AJPIは円に内接(∵∠AJP=∠AIP=π/2)するので、∠IAJ+∠IPJ=π。
他方、△ABCは正三角形なので∠IAJ=π/3。よって∠IPJ=2π/3。
同様に、∠HPJ=∠HPI=2π/3。このことを用いて、
| T | =△HPI+△IPJ+△JPH
|
| =1/2・xy・sin(2π/3)+1/2・yz・sin(2π/3)+1/2・zx・sin(2π/3)
|
| =√3/4・(xy + yz + zx) …(答)
|
(3)また、前回みたいに反則を使います(笑)。
U=T-k・(x + y + z - √3/2)
・・・とおいて、多変数関数の最大最小問題にしてしまいます。
∂U/∂x = √3/4・(y + z) - k
∂U/∂y = √3/4・(z + x) - k
∂U/∂z = √3/4・(x + y) - k
∂U/∂k = x + y + z - √3/2
上記4本の式が全て 0 になることから、まず前3者から x = y = z = 2√3/3・k を得ます。
これを第4式= 0 に代入して整理すると、k = 1/4 、従って x = y = z = √3/6 を得ます。
このときU、従ってTは最大で、Tの最大値は √3/16 = 1/4・S
これより題意の不等式 4T≦S が成立します。
等号成立の場合は、上記の通りです。
通常、大学入試では、例えば z を消去して x, y の2変数関数にして、変数の変域に注意しながら例えば x を固定して y を動かしたときの暫定最大値 g(x) を求め、0 < x ≦ √3/2 のもとでの最大値を求める…という手続きで解くのでしょうか。或いは、うまく不等式を運用して解いちゃったりするのでしょうか?
上記(3)の等号成立時の点Pが重心であることの証明は、屋上屋を重ねるようで
恐縮ですが、後日 NO.1322 最大・最小となる点(2)
の最後の部分の訂正を以て、NO.1327 最大・最小となる点(3)のニースケンスさ
んのコメントに対するお応えも兼ねて行えればと思います。
#それにしても、類題って多いんですね。(^^;

| NO.1360
| 2003.2.17. | yokodon | 2乗して下の桁が不変な整数(1)
|
~模試シリーズ16~
(1)2桁の整数 25 を平方すると 625 となり、下2桁は不変である。こうした2桁
の整数は 25 の他にもあるか。
(2)3桁の整数で、平方して下3桁が変わらないものを全て求めよ。
#お時間のある方は、4桁、5桁、・・・で同様にお考えになってみては如何でしょう。

| NO.1361
| 2003.2.18. | teki | 2乗して下の桁が不変な整数(2)
|
やってみたところ、2桁では、25の他に76があります。
3桁では、376、625の2つですが、4桁では、9376の1つだけのようです。
もう片方の○625のほうは、625の2乗の下4桁が0625となってし
まうので、該当がないようです。
探し方は、比較的簡単です。
1桁の場合、2乗して変わらないのは、1、5,6の3つですが、1の場合は、2桁にすると01となるため、前出の625の4桁と同様、2桁以降は該当なしになります。
結局、4桁以上で該当するのは、6の系統だけのようです。

| NO.1362
| 2003.2.18. | kiyo | 2乗して下の桁が不変な整数(3)
|
十進ベーシックで出力しました。なんとなく懐かしく思います。
関係性を保つためにペアにこだわりました。
| n | n2
|
|---|
| 5 | 25
|
| 25 | 625
|
| 625 | 390625
|
| 90625 | 8212890625
|
| 890625 | 793212890625
|
| 2890625 | 8355712890625
|
| 12890625 | 166168212890625
|
| 212890625 | 45322418212890625
|
| 8212890625 | 67451572418212890625
|
| 18212890625 | 331709384918212890625
|
| 918212890625 | 843114912509918212890625
|
| 9918212890625 | 98370946943759918212890625
|
| 59918212890625 | 3590192236006259918212890625
|
| 259918212890625 | 67557477392256259918212890625
|
| 6259918212890625 | 39186576032079756259918212890625
|
| 56259918212890625 | 3165178397321142256259918212890625
|
| 256259918212890625
| 65669145682477392256259918212890625
|
| 2256259918212890625
| 5090708818534039892256259918212890625
|
| 92256259918212890625
| 8511217494096854352392256259918212890625
|
| 392256259918212890625
| 153864973445024588727392256259918212890625
|
| 7392256259918212890625
| 54645452612300005057477392256259918212890625
|
| 77392256259918212890625
| 5989561329000849809744977392256259918212890625
|
| 977392256259918212890625
| 955295622596853633012869977392256259918212890625
|
| 9977392256259918212890625
| 99548356235275381465044119977392256259918212890625
|
| 19977392256259918212890625
| 399096201360473745722856619977392256259918212890625
|
| 619977392256259918212890625
| 384371966908872375601191606619977392256259918212890625
|
| 6619977392256259918212890625
| 43824100673983991394155879106619977392256259918212890625
|
| 106619977392256259918212890625
| 11367819579125235975036734004106619977392256259918212890625
|
| 4106619977392256259918212890625
| 16864327638717175315320739859004106619977392256259918212890625
|
| 9004106619977392256259918212890625
| 81073936023920699329853843152771109004106619977392256259918212890625
|
| n | n2
|
|---|
| 6 | 36
|
| 76 | 5776
|
| 376 | 141376
|
| 9376 | 87909376
|
| 109376 | 11963109376
|
| 7109376 | 50543227109376
|
| 87109376 | 7588043387109376
|
| 787109376 | 619541169787109376
|
| 1787109376 | 3193759921787109376
|
| 81787109376 | 6689131260081787109376
|
| 40081787109376 | 1606549657881340081787109376
|
| 740081787109376 | 547721051611007740081787109376
|
| 3740081787109376
| 13988211774267263740081787109376
|
| 43740081787109376
| 1913194754743017343740081787109376
|
| 743740081787109376
| 553149309256696143743740081787109376
|
| 7743740081787109376
| 59965510454276227407743740081787109376
|
| 607743740081787109376
| 369352453608598807478607743740081787109376
|
| 2607743740081787109376
| 6800327413935747244982607743740081787109376
|
| 22607743740081787109376
| 511110077017207231620022607743740081787109376
|
| 80022607743740081787109376
| 6403617750108490103144731780022607743740081787109376
|
| 380022607743740081787109376
| 144417182396352539175410357380022607743740081787109376
|
| 3380022607743740081787109376
| 11424552828858793029898066613380022607743740081787109376
|
| 893380022607743740081787109376
| 798127864794612716138610952755893380022607743740081787109376
|
| 5893380022607743740081787109376
| 34731928090872050116956482046515893380022607743740081787109376
|
| 995893380022607743740081787109376
| 991803624372854204655478894958610995893380022607743740081787109376
|

| NO.1363
| 2003.2.19. | 本多欣亮 | ドラマ「高校教師」
|
みなさん、放映中のドラマ「高校教師」は御覧になってますか?
数学の教師が主人公の、ちょっと(かなり)切なくもインモラル、非現実的な
ようで引き込まれそうになるどきどきするドラマです。
この数学教師の自宅の部屋には、クリア(透明)なホワイトボードがあって、その板上で毎週数学ねたを小出しに披露してくれます。
対角線論法だったり、四元数だったり、暗号論だったり・・・。
で、この格好いいホワイトボードが実在するものなのかどうか、「高校教師」
のインテリアを提供している東京原宿のショップPostDetailさんに、直接お話を伺ったところ、
「あのホワイトボードは、残念ながら実在するものではありません。ドラマ用
に美術さんが製作したものです」
との回答でした。でも、
「アクリル板(これはとても高価)には、描いたり消したりできるマーカーが
あるので、実際の製作は可能です」
ともおっしゃってました。たぶん、PET 素材などを使えば、もっと廉価に製作
可能かもしれません。以上、ちょっと変わった数学関係の話題でした♪

| NO.1364
| 2003.2.20. | kirkland | 垂足三角形(3)
|
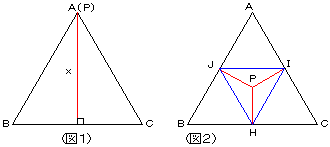
| A君 | 「突然ですが、点PをAにとるとy=z=0になるから、x+y+zは△ABCの高さと一致しますよね。(図1)
というわけで、(1)は終了。(2)はパス。(3)は、何となくそんな気がするじゃないですか。ちょうど点Pがど真ん中に来るとき、△HIJが正三角形になって、面積が最大になるような感じがしますよ。面積もちょうど4分の1になるし。(図2)」
|
| 先生 | 「(1)はまだしも、(3)なんか予想だけじゃないか!」
|
| A君 | 「いやぁ何てったって、推測三角形っていうぐらいだし。」
|
| 先生 | 「お前なぁ、それが言いたかっただけだろ!
そもそも、平方根も知らないのに、小学生に解けるわけないだろ!中3の兄さんを連れてこい!」
|
| A君 | 「まあまぁ、そんなに怒らないでヒントをください。」
|
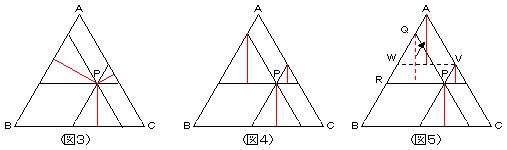
| 先生 | 「そうだなぁ、点Pを通って各辺に平行な線を引くてみなさい(図3)。」
|
| A君 | 「なんか、正三角形がたくさんできましたね。正三角形だと高さはどこでも同じだから、高さの向きを変えて(図4)。
点Vを通ってBCと平行になるようにVWを引くと、△AWVと△QRPは合同になるので、また高さを移動できます(図5)。すると、3本の赤線の長さの和は、正三角形ABCの高さと等しくなりますね。」
|
| 先生 | 「素晴らしい。珍しく冴えてるねぇ。」
|
| A君 | 「ところで、正三角形ABCの高さはどうやって求めるんですか?」
|
| 先生 | 「小学生には無理だ。一辺が1なので、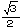 ということになるんだけどね。(2)もこの数値を使うから君には無理だ。」 ということになるんだけどね。(2)もこの数値を使うから君には無理だ。」
|
| A君 | 「でも、正三角形の高さが一辺の何倍になっているかが分かれば、解けそうな気がしますよ。∠ⅠPHはいつも120°
なんだから△ⅠPHは、PHを底辺にして考えると面積が出そうですよね。(図6)」
|
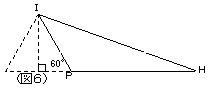
| 先生 | 「まぁ、そんな感じでいいだろう。しかし、(3)は小学生には少し難しいぞ。平方根を使わないでやってみよう。さて突然なんだが、正方形が3個あって、一辺の長さの和が1のとき、面積の和の最小値を考えてみよう。」
|
| A君 | 「何とも唐突な!う~ん、(図7)のような感じですよね。この3つの正方形の面積の和は、赤の長方形の面積よりも小
さいわけだから、赤の長方形の面積が最小になるときを考えればよいわけで……。高さが最小になればいいので、そのときの高さは3分の1ですね。このとき、正方形は3つとも同じ大きさです(図8)。」
|
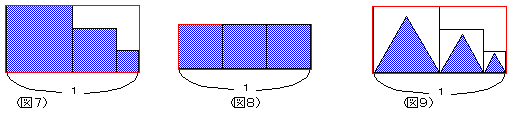
| 先生 | 「その通り。これが3つの正三角形でも同じだということが分かるかな。正三角形の底辺と高さの比は一定だから。」
|
| A君 | 「何となく分かります。一辺の長さが3分の1ずつのとき、面積の和は最小になるんですね。ところで、話があさっての方向へ向かっているような気が……。」
|
| 先生 | 「さて、話を元に戻そう。(図10)をみてごらん。基本的には(図3)と同じで、点Pを通って各辺に平行に引いたのが、RU、QT、SVだ。△HⅠJ(青)と△TVR(緑)が相似なのは分かるかな?PHとPTの関係を考えれば分かると思うんだけど。」
|
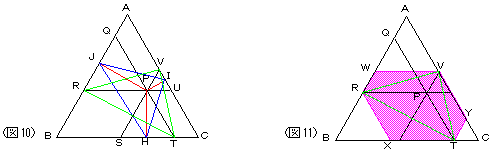
| A君 | 「何か、嫌がらせのような図ですね。PTは、Pを中心にしてPHを30°回転させて、一定の割合  で拡大したものですね。PV、PRも同じです。というわけで、青と緑の三角形は常に相似で、その相似比も常に一定ということになりますね。次が読めましたよ。△HⅠJ(青)が最大になるときに△TVR(緑)も最大になるので、緑で考えようという魂胆ですね。」 で拡大したものですね。PV、PRも同じです。というわけで、青と緑の三角形は常に相似で、その相似比も常に一定ということになりますね。次が読めましたよ。△HⅠJ(青)が最大になるときに△TVR(緑)も最大になるので、緑で考えようという魂胆ですね。」
|
| 先生 | 「まぁ、いい線いってるね。しかしこれだけではまだ不十分。さらに補助線を引くよ。V、R、Tを通って、それぞれBC、CA、ABに平行になるようにVW、RX、TYを引くと…(図11)。」
|
| A君 | 「平行四辺形がたくさんできますね。六角形WRXTYV(ピンク)の面積は、△RTV(緑)の2倍です。しかも、素晴らしいことにピンク以外の3つの三角形は3つとも正三角形ですね。しかも、WR=VP=YTだから、一辺の長さの和は1ですね。これでさっきの話に繋がりましたね。」
|
| 先生 | 「まとめると、3つの正三角形の面積が最小(一辺がそれぞれ3分の1)になるとき、ピンクの面積は最大。そのとき、緑も最大で青も最大になるというわけだ。」
|
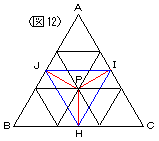
| A君 | 「あとは、図を描けば終わりですね。Q~Vをそれぞれの辺の3等分点にして……(図12)。なんかそれっぽくなりましたね。Pはど真ん中に来ますもんね。」
|
| 先生 | 「重心というんだよ。」 |
| A君 | 「獣神サンダーライガー?ところで、もう少しまともな解き方はないんですか?」
|
| 先生 | 「コーシー・シュワルツの不等式っていうのを使えば綺麗なんだけど、小学生には無理だ。」
|
| A君 | 「コーヒー?シュワルツネッガー?」
|

 E-mail
E-mail
 戻る
戻る
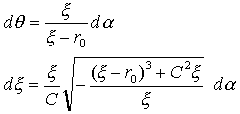 (1)
(1)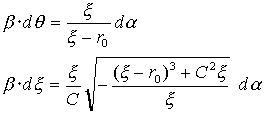 (2)
(2)



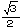 ということになるんだけどね。(2)もこの数値を使うから君には無理だ。」
ということになるんだけどね。(2)もこの数値を使うから君には無理だ。」
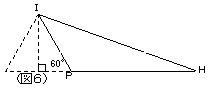

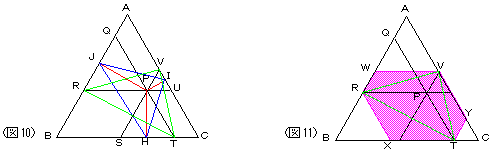
 で拡大したものですね。PV、PRも同じです。というわけで、青と緑の三角形は常に相似で、その相似比も常に一定ということになりますね。次が読めましたよ。△HⅠJ(青)が最大になるときに△TVR(緑)も最大になるので、緑で考えようという魂胆ですね。」
で拡大したものですね。PV、PRも同じです。というわけで、青と緑の三角形は常に相似で、その相似比も常に一定ということになりますね。次が読めましたよ。△HⅠJ(青)が最大になるときに△TVR(緑)も最大になるので、緑で考えようという魂胆ですね。」

 E-mail
E-mail
 戻る
戻る