
Weekend Mathematics/コロキウム室/2000.1~3/NO.89
| NO.767 | 2000.3.1. | Junko | 「三角の問題」の発展(3) |

なつかしいゼ-タ-関数の登場ですね。

| NO.768 | 2000.3.1. | 水の流れ | 「三角の問題」の発展(4) |
「Mathematica」にこんな計算をさせて、あの角度の和の極限を見ま
したので,報告します。
有限積(1+i/k)(k=1,2,3,・・・)をしまして、その偏角をみました。
もちろん,k=3のときは,90度になります。
k=16と17の間で180度を越えます。
k=81と82の間で270度を越えます。
k=396と397の間で360度を越えます。
したがって、
k=無限大の無限積(1+i/k)の結果はcomplex infinityになります。
それと、arctan x をi とlog で表せましたし,そこから、ご存じの
オイラーのeiα=cosα+isinα の有名な式もでてきました。
そして、これを使って,角度の和をlog の和や差で表されましたが、
無限大の極限値にもっていけないのです。
ここのところが、ゼーター関数,ガンマ関数,オイラー定数が関連するのかな?

| NO.769 | 2000.3.2. | WAHEI | ガロア理論の心(1) |
(体の代数拡大と指標の独立性)
今回から、ガロア理論を考えてみたいと思います。
これまでの リングセオリーシリーズと
代数方程式シリーズの内容を踏まえれば
この理論を展開する事は、それほど大変な事ではありませんが、
まだ全くやっていない概念もいくつかありまして、
その中で最も基礎的なものは線形代数です。
実はガロア理論は線形代数の知識を使うと意外なほどにすっきりとします。
もともと線形代数は連立方程式論との関係が深いですから、それも当然かもしれません。
それをわかりやすい形で初めて世の中に伝えたのはEmile-Artin先生です。(この人は大先生)
(定義)
Kを体として、kがKの部分体とは、kはKの部分環であってかつk内の0でない元が全て
unitを成す事をいう。この状態をK/kと書いて、Kをkの拡大体という。
上の定義のK/kを「体の拡大」といいます。
最も典型的な体の拡大は複素数体Cと有理数体Qです。
つまりC/Q。
(以下Zと書いたら整数環、Qを有理数体、Rを実数体、Cを複素数体とします。
今まではRと書いたら環を表す事が多かったですが、
これからはAとかBとか書いて環を表します。
この環については断りますが、Z、Q、R、Cについてはいちいち断らない事とします。ご注意)
さて、K/kを体の拡大とします。
k[X]を体k上の多項式環とします。
これは環でしたからこのk[X]を係数とする2変数の多項式環、(k[X])[Y]が作れます。
これをk[X、Y]と書いて2変数の多項式環といいます。
帰納的にn変数の多項式環を次で定義します。
k[X1、X2、・・・、Xn]:=(
k[X1、X2、・・・、Xn-1])[Xn]
ここで代入原理から、Sをkの部分体としますと、Sからkへ内部写像が取れて、
これは環写像ですから、
φ:S[X1、X2、・・・Xn]→kでφ(Xi)=αiなる代入射が取れます。
(但し1≦i≦nで、αiはKの元)この代入射φのイメージ、
つまりIm(φ)をS(α1、α2、・・・αn)と書いて、Sにαiを添加した体といいます。
もう大分昔のことかもしれませんが、
NO.699 代数方程式の代数的解法(1)で書いたことを
数学的に書き直したものです。
与えられた方程式を代数的に解くとは定義体に累乗根を次々と添加していき、
全ての根がその定義体の拡大体に含まれるように拡大の列が取れることでした。
(ベクトル空間について)
今はリングセオリーではないので、ここではよく使われるベクトル空間の定義を書きます。
後で余裕があるようでしたら環を用いてこのベクトル空間を一般化します。
(定義)
アーベル群Vが以下の条件を満たすとき体K上のベクトル空間という。
まず、写像K×V→Vが、(a、m)→amと定まっていて、∀a、b∈K、∀m、n∈Vに対し
(定義)
n個のベクトルa1、a2・・anがK上一次独立であるとは、
α1a1+α2a2+・・・+αnan=0⇒
α1=α2=・・・=αn=0に限る事をいい、
a1、a2・・・anがK上一次従属であるとは、
少なくとも1つは0でないαiがあって、α1a1+・・・+αnan=0を満たす事をいう。
但しαiはKの元である。
この一次独立や一次従属などは、ベクトル空間の中では最も基本的な言葉です。
(定義)
一次独立なベクトルの最大個数をそのベクトル空間の次元という。
ベクトル空間Vの次元がnであれば、この事をdimV=nと書く。
これもやはり大切な概念です。「体K上」のベクトル空間ということを強調する場合
、Vの次元がnである事を[K:V]=nと書きます。
K/kを体の拡大とすれば、写像k×K→K、(c、x)→cxをうまく定めれば、
Kはk上のベクトル空間になります。
そして、[K:k]でk上ベクトル空間Kの次元を表す事とします。
この次元を拡大次数といいます。
この場合、スカラーは狭いkの方から取ってきていることに注意してください。
(定義)
α∈Kがk上代数的(algebraic)であるとは、
f(α)=0を満たすk[X]の元f(X)が存在する事をいう。但しf(X)≠0とする。
代数方程式の根になる数を代数的といいますが、
これはその概念を一般の体に拡張したものです。
πとかは代数的でない数として有名です(これを証明したのはエルミートという人)。
代数方程式の根になる数というのはよくよく考えてみますと、
コンパスと定規を用いて作図可能な数という事になります。
例えば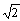 などは1辺が1の正方形の対角線になります。
そうすると、代数的でない数はコンパスと定規を使って作図できない数という事です。
古代から角の3等分線は作図できない事が知られていますし、
与えられた円に等しい面積の正方形の作図もできません。これはπが代数的でないからです。
などは1辺が1の正方形の対角線になります。
そうすると、代数的でない数はコンパスと定規を使って作図できない数という事です。
古代から角の3等分線は作図できない事が知られていますし、
与えられた円に等しい面積の正方形の作図もできません。これはπが代数的でないからです。
α∈Kに対し、写像φ:K[X]→Kをφ(X)=αで定めます。
代入原理からそれは可能でした。
さてこの代入射φのカーネルを考えます。
Ker(φ)=Iとおきます。このときαが代数的⇔I≠{0}です。
なぜなら、αが代数的ならば定義から、f(α)=0なるf(X)≠0がk[X]から取れて、
このことはf(X)∈Iを意味しています。
よってI≠{0}です。逆にI≠{0}を仮定しますと、
0でない元がIの中にあって、それをg(X)とおくと、カーネルの定義から、
φ(g(X))=g(α)=0ですから、αは代数的です。
K[X]はNO.751 リングセオリー(19)の問題13で見たようにPIDでした。
ですからI=(p(X))と書けます。(p(X)∈K[X]です。)
今、p(X)≠0ならばばKが体である事から、その最高次係数をくくりだして、
p(X)の最高次係数が1になるようにできます。
(最高次係数が1の多項式をmonicな多項式といいます)かつp(X)の次数を最小に取ります。
このp(X)をαの最小多項式といいます。
実際、p(X)とは異なるf(X)について、f(α)=0ならば、p(X)|f(X)となります。
このことからも、最小というイメージがつかめると思います。
それから、p(X)|f(X)は整数環の時と同様に、
f(X)=p(X)g(X)なるg(X)が取れることを意味します。
また次数の最小性からp(X)が既約であることもわかります。
従って(p(X))は素イデアルであって、(0)でないから極大イデアルで
(なぜならK[X]も、k[X]もPID)よって、k[X]/Iは体となります。
これは第一同型定理からk(α)と同型です。つまりk[X]/I~k(α)です。
ここで、k[X]/Iの具体的な形について考えてみましょう。
deg(p(X))=nとおきますと、p(X)はmonicですから、
p(X)=a0+・・・・+Xnと書けます。
∀g(X)∈k[X]を取ってきてp(X)で割ります。
すると、
g(X)=p(X)q(X)+r(X)
但しr(X)=0か、deg(r(X))<deg(p(X))
今p(α)=0を考えれば、g(α)=r(α)ですから、
k[X]/I~k(α)={a0+・・・an-1αn-1|ai∈k}
となっています。
さらに、1、α、α2、・・・αn-1は一次独立になっています。
(その証明)
a0+a1α+・・・+an-1αn-1=0とすると、
αはg(X)=a0+a1X+・・・+an-1Xn-1の根ですが、
αの最小多項式はp(X)でその次数はnですから、
nより次数が小さい多項式の根とはなりません。
よって、g(X)=0より、a0=・・・=an-1=0となって、
1、α、・・αn-1は一次独立です。
そして、[k(α):k]=nがわかりました。 (証明終わり)
つまり、k(α)/kですが、その拡大次数はαの最小多項式p(X)の次数となっている事が
わかりました。以上の考察からわかった事をまとめてみれば、次の大切なコロラリーを得ます。
(コロラリー)
α∈Kのとき、次は同値である。

| NO.770 | 2000.3.2. | 水の流れ | 「三角の問題」の発展(5) |


この公式は指数関数と三角関数の統一が虚数によって見事に表されています。
以上が、この問題を考えているときに出てきた、副産物です。
ここまでは、<参考文献:数学の愉しみ創刊号(日本評論社)>から抜粋です。
また、①をこのように変形しても出てきます。
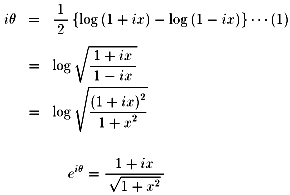
になって、後は同じです。
さて、本題ですが、

これを[Mathematica]で計算しました。
また、図形的にも、直角を挟む2辺を1と1/nとする三角形を、
次々とオウム貝のように螺旋上に重ねていったとき、
その合計の角の和は、どれだけでも大きくなっていきます。
したがって、求める和は無限大になります。

| NO.771 | 2000.3.5. | WAHEI | ガロア理論の心(2) |
前回からの続きです。
(定義)
K/kを体の拡大とし、これが代数的(algebraic)であるとは∀α∈Kがk上代数的になっている事
をいう。
さて、ここからが今回の本題です。
(面白そうな方程式)
f(x)=x3-2∈Q[x]とします。
この根はα、αω、αω2の3つであることはわかると思います。
但しαは2の3乗根、ωは1の立方根です。
従ってω2+ω+1=0を満たします。
さて、定義からこの3つの根はQ上代数的でかつ、Q(α、αω、αω2)⊆Cです。
αの最小多項式をp(x)とおきますと前回見たように、
[k(α):k]=deg(p(x))でした。
すなわち拡大次数は最小多項式の次数に等しいのです。
いま、αの最小多項式(もちろんQ上の)はx3-2ですから、
従って[Q(α):Q]=3です。
それから同じようにωのQ上最小多項式はx2+x+1なので[Q(ω):Q]=2です。
ああ、それから、αやωはQの元ではありませんから、
当然Q(α)⊃QとQ(ω)⊃Qが成り立っていますよ。
次に[Q(α、αω、αω2):Q(ω)]と、
[Q(α、αω、αω2):Q(α)]を求めたいのです。
そのためには次の補題が必要でしょう。
(補題1)
Q(α、αω、αω2)=Q(α、ω)が正しい。
(証明)
まず、Q(α、αω、αω2)⊂Q(α、ω)はいえると思います。
といいますのも、α、ω∈Q(α、ω)ですから、
Q(α、ω)が体である事を考えれば、αω、αω2∈Q(α、ω)だからです。
次に逆の包含関係です。
α、αω∈Q(α、αω、αω2)ですから、
やはりQ(α、αω、αω2)が体である事を考えると、
α‐(αω)=ω∈Q(α、αω、αω2)だからです。
よってQ(α、αω、αω2)=Q(α、ω)です。 (証明終わり)
この補題によると、求めたい物は[Q(α、ω):Q(ω)]と、
[Q(α、ω):Q(α)]に化けました。
ところで、2変数多項式の定義はAを環とするとA[x、y]=(A[x])[y]でしたから、
Q(α、ω)=(Q(α))(ω)です。
ですから[Q(α、ω):Q(ω)]を求めるにはQ(ω)上αの最小多項式の次数を
求めれば良いという事になりますね。それをg(x)とおきます。
するとα3-2=0ですから、g(x)|x3-2となります。
よって適当な多項式s(x)を用いてx3-2=g(x)s(x)です。
ところが左辺は既約な多項式ですから、s(x)定数ということになりdeg(g(x))=3
である事がわかります。だから[Q(α、ω):Q(ω)]=3です。
同じように[Q(α、ω):Q(α)]を求めます。
Q(α)上ωの最小多項式をh(x)とします。
するとh(x)|x2+x+1ですから、
x2+x+1=h(x)m(x)と書けます。
左辺は既約ですから、m(x)は定数で、従ってdeg(h(x))=2ですから、
[Q(α、ω):Q(α)]=2となります。
体の拡大次数nの体の拡大K/kを「k→(n)K」で書くことにします。
つまり矢印の行き先が拡大体となっているように書き、
拡大体と矢印の間に拡大次数を書きます。
すると、今考察したことを下のような図に書く事ができます。
Q→(3)Q(α) ↓ ↓ (2) (2) Q(ω)→(3)Q(α、ω)⊂C
(補題2)
M→(a)N→(b)Kを有限次拡大の体の拡大列とすると、[K:M]=abが正しい。
この補題が言っている事はつまり、[K:N]=b、[N:M]=aでaとbが共に有限ならば、
[K:M]=[K:N][N:M]が成り立つといっています。
それを認めるならば[Q(α、ω):Q]=2・3=6となります。
この補題2の証明ですが、ベクトル空間においての基底の概念をまだはっきりと書いていないので、
それを書いてから証明したいと思います。
(ものすごく簡単な証明ですから、基底や次元についての概念をお持ちの方はやってみてください)
Q(α、ω)=Eとおいて、このEを方程式f(x)=x3-2の分解体といいます。
分解体上では方程式はバラバラに因数分解していることがわかると思います。
またAutE={σ|σ:E→E環同型}とおきますと、
写像の合成を演算に群を成しました
(NO.706 代数方程式の代数的解法(4)を参照)。
このAutEをE上の自己同型群といいます。
ガロア理論の本質はこの自己同型群の部分群と中間体の間に一対一の対応があるという事でした
(NO.706 代数方程式の代数的解法(4)を参照)すなわち、
今の例では、次の集合AとBの間には一対一の対応があります。
A={K|Q⊆K⊆Eなる中間体}
B={H|H<AutE}
但し、H<AutEとは、HはAutEの部分群であることを意味します。
今後この書き方はよく使いますから覚えておいてください。
さて、具体的な対応のつけ方を語る前に言葉を定義します。
Gal(E/K):={σ|σ∈AutEで、∀a∈Kに対してσ(a)=a}
つまりKの元を皆固定するE上自己同型群をこのようにGal(E/K)とかきます。
また、E(H):={x∈E|∀σ∈Hに対しσ(x)=x}として、これをHに対する不変体といいます。
つまりHの元(これは写像)によって動かないEの元です。
また、Gal(E/K)はAutEの部分群となっていて、またE(H)は上のAの元です。
つまり中間体となっています。
(その証明)
まず、恒等写像1は全ての元を固定するE上自己同型ですから、
1∈Gal(E/K)より、Gal(E/K)≠φです。
次に∀τ、σ∈Gal(E/H)を取ってくると、∀a∈Kに対し、τ(a)=a、σ(a)=aで、
従って、a=σ‐(a)です。
よって、τσ‐(a)=τ(σ‐(a))=τ(a)=aより、
τσ‐∈Gal(E/K)ですから、
部分群の定義からGal(E/K)はAutEの部分群です。
従ってGal(E/K)∈B
まや、E(H)が中間体である事を言うので、つまりEの部分体になっている事を言います。
∀σ∈Hに対し、σ(1)=1ですから(なぜならばσは環写像)、
1∈E(H)より、E(H)≠φ。
∀a、b∈E(H)に対し
σ(ab)=σ(a)σ(b)=ab、σ(a+b)=σ(a)+σ(b)=a+b、
σ(-a)=-σ(a)=-aより、ab、a+b、-a∈E(H)で、
さらに、0≠∀a∈E(H)から取ると、Eが体であることからa‐が存在して、
aa‐=1なので、
σ(aa‐)=σ(1)=1⇔σ(a)σ(a‐)=1
よってσ(a)‐=σ(a‐)⇔a‐=σ(a‐)であって、
a‐∈E(H)となり
E(H)はEの部分体ですから、E(H)∈Aです。 (証明終わり)
このことから、集合AとBの間には次のような対応がついていることがわかりました。
B∋H→E(H)∈A
A∋K→Gal(E/K)∈B
今は方程式x3-2について考えています。
それから、Gal(E/K)を方程式x3-2の分解体EにおけるK上ガロア群といいます。
代数方程式が代数的に解けるためには、
このガロア群が可解である事が必要かつ十分であることが証明されます。
ここで実際にガロア群の計算に入りましょう。
(例1)
m∈Qとし、√mを無理数とします。
ここでf(x)=x2-mのQ上ガロア群を求めてみたいと思います。
まずこの方程式の分解体EはもちろんQ(√m)です。
求めるべきはGal(E/Q)=Gal(Q(√m)/Q)ですね。
ここから少し受験っぽいテクニックを使います。
∀φ∈Gal(E/Q)に対して、今考えなければならない事は無理数である√mがどう移るかです。
といいますのもQ上の環写像はすべて恒等写像ですから
(NO.751 リングセオリー(19)の問題を参照)。
ここで、0=φ(0)=φ((√m)2-m)=φ(√m)2-φ(m)ですから
(ここが受験時代に培ったセンスの発揮所です)、
φ(m)=mを考えて(なぜなら、くどいですが、Q上の環写像は恒等写像なので)
m=φ(√m)2です。
従ってφ(√m)=±√mである事がわかります。
f(x)=0なる方程式の根はもちろん±√mですから、φ(√m)はf(x)の根です。
ここがポイントです。
つまりここから方程式上のガロア群はその方程式の根の置換を引き起こす事が予想されるのです
(それが正しいことをすぐに証明します)。
さて、分解体E=Q(√m)の任意の元はa+b√mという形をしているので(なぜならQ(√m)
は多項式環Q[x]に√mを代入したのもだから)、
a、b∈Qを考えてφ(a+b√m)=φ(a)+φ(b)φ(√m)=a±b√mです。
よってφ(√m)=√mならばφは恒等写像1です。
またφ(√m)=-√mならば、φはEの元をa-b√mに移す事がわかりました。
従ってGal(E/Q)=Gal(Q(√m)/Q)={1、φ}である事がわかります。
但しφはφ(a+b√m)=a-b√mなる環同型です。
この場合は方程式f(x)=0上のガロア群は位数2の群であることがわかりました。
(方程式上のガロア群の元はその方程式の根を置換する写像となっている事の証明)
Kを体としEをf(x)∈K[x]の分解体とする。
Gal(E/K)∋∀φに対して、f(x)=a0+a1x+・・・anxnとする。
φはKの元を固定するE上の自己同型なのでこの場合、
f(x)の係数を全て固定するので、
φ(f(x))=a0+a1φ(x)+・・・+anφ(x)nだが、
f(x)の根をαとすると、
f(α)=0なのでφ(f(α))=a0+a1φ(α)+・・・+anφ(α)n=0。
従ってαがf(x)の根ならばφ(α)もf(x)の根である。 (証明終わり)
このことは簡単な事ですが、極めて重要な事です。
(例2)
f(x)=x2+1を考えて、この方程式のQ上のガロア群を今度は求めてみましょう。
この方程式の分解体はQ(i)で、従って求めるべきはGal(Q(i)/Q)です。
Q上の環写像は全て恒等写像です(できる限りこれを確かめて下さい。但し少し高級です)。
ですから例1と同じようにして、Gal(C/R)={1、φ}です。
但しφ(a+bi)=a-biです。
このガロア群ではf(x)=0の根±iで、
i→-iと-i→iと根を置換していることに注意してください。
今回はこれくらいにして、次回からいよいよ前半の山である、
「指標の独立性」を考えて見ましょう。
ところで、ぜひ皆さんも適当な方程式を作って定義体
(NO.699 代数方程式の代数的解法(1)参照)に根を添加して図などを書いて「遊んで」みてください。
世界が広がる事を保証いたします。

| NO.772 | 2000.3.5. | 水の流れ | 無限積(1) |
太郎さんは、数式ソフト「Mathematica Versin4」をWOLFRAM社から、
購入しました。
分からないままに、使っていましたところ、次のような無限積を求めてくれません。
しかし、n=10、100、1000、10000、・・・・とすると極限値を求めてくれます。
太郎さんは、この値がある極限値に収束していると思っています。
真の値に至るまでの過程を皆さん、教えてください。
問題:
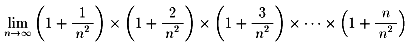
の極限値を求めたいのですが、
とりあえず、「Mathematica」にやらせてみましたところ、以下のようになりました。
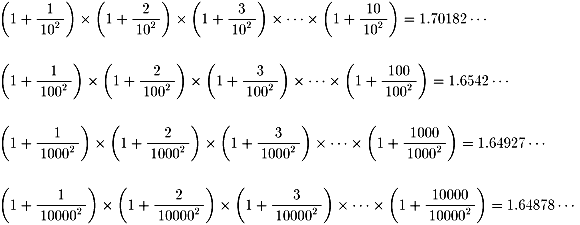

| NO.773 | 2000.3.7. | 月の光 | 無限積(2) |
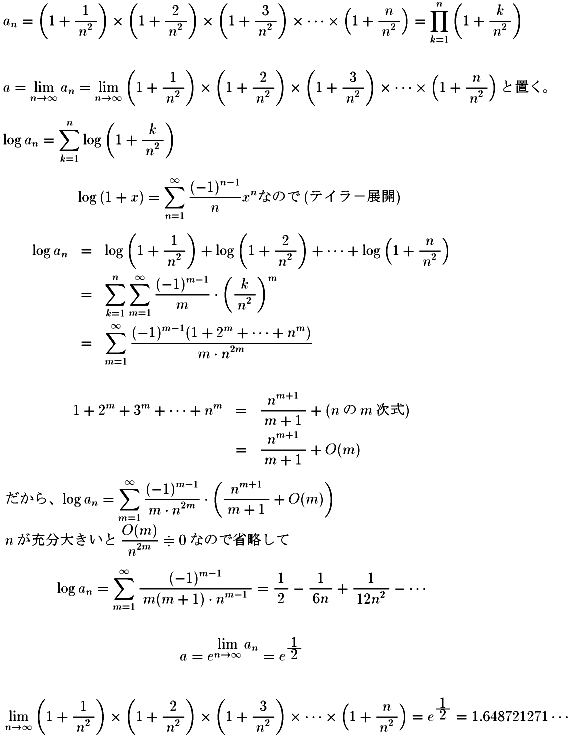
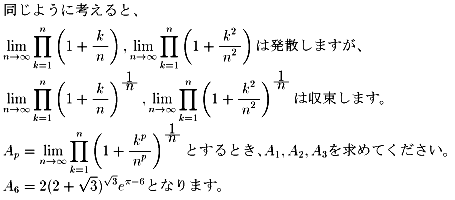

| NO.774 | 2000.3.7. | 水の流れ | 階乗関数(1) |
皆さんは、nの階乗はn!=n(n-1)(n-2)・・・3×2×1ということをご存じです。
では、xの階乗関数はx[k]=x(x-1)(x-2)・・・(x-k+1)
と表される関数をいいます。
例えば、
x[1]=x,x[2]=x(x-1),
x[3]=x(x-1)(x-2)、x[4]=x(x-1)(x-2)(x-3)、
x[5]=x(x-1)(x-2))(x-3)(x-4)、・・・・・・です。
ここで、問題です。
x2=S(2,1)x[1]+S(2,2)x[2] となる
係数S(2,1)、S(2,2)を求めてください。
さらに、x3=S(3,1)x[1]+S(3,2)x[2]+
S(3,3)x[3]となる係数S(3,1)、S(3,2)、S(3,3)を求めてください。
そして、
一般に、xn=S(n,1)x[1]+S(n,2)x[2]+
S(n,3)x[3]+・・・+S(n,n)x[n]となる
係数S(n,1)、S(n,2)、S(n,3)、・・・、S(n,n)を求めてください。
係数S(n,1)、S(n,2)、S(n,3)、・・・、S(n,n) を連続組立除法で解いてみてください。
ちょっとした発見ができますよ。

| NO.775 | 2000.3.8. | kiyo | 階乗関数(2) |
「Triangle of Stirling numbers of 2nd kind」 の求め方は、 大別して以下の4通りがあるようです。
Formula: S2(n,k) = k*S2(n-1,k)+S2(n-1,k-1), n>1. S2(1,k) = 0, k>1.
S2(1,1)=1.
E.g.f. m-th column: ((exp(x)-1)^m)/m!.
S2(n,k) = (1/k!) * Sum_{i=0..k} (-1)^(k-i)*C(k,i)*i^n.
Example: 1; 1,1; 1,3,1; 1,7,6,1; 1,15,25,10,1; ...
Program: (PARI) S2(n,k) =
if(k<1|k>n,0,if(n==1,1,k*S2(n-1,k)+S2(n-1,k-1)));
printp(matrix(9,9,n,k,S2(n,k)))

| NO.776 | 2000.3.8. | ヴァ- | 無限級数の和(12) |
最近 Weekend Mathematics から遠ざかっていたのですけど,
久しぶりに覗いてみると「無限級数の和」という興味深いテーマがあって
楽しんでしまいました.
よく考えると,以前(といってもすごーく前ですが)
私が投稿した
NO.106 プレゼントの問題(15)
の h(m) が Junko先生の
NO.757 無限級数の和(8)における
Am-1に相当していますね.
「プレゼントの問題」
と「無限級数の和」の一連のお話は
何か関係があるのかもしれませんね.

 E-mail
E-mail
 戻る
戻る