Weekend Mathematics/コロキウム室/テーマ別/33.代数方程式の代数的解法1
コロキウム室(代数方程式の代数的解法・その1)
| NO.699
| '99 12/29 | WAHEI | 代数方程式の代数的解法(1)
|
part 1
もうすぐ2000年でいろいろな問題がとり立たされているようですけれど、さしあ
たって興味のある問題は代数方程式の代数的解法についてです。
大昔から4次方程式までは根の公式を用いて解けることが知られていました。
根の公式を用いて解くことを代数的に解くといいます。
いわゆる4則演算が定義されている集合を体といいますが、
この体を用いて代数方程式の構造を解明したのがアーベルであり、
演算が1つしか与えられていない集合である群を用いてアーベルと同じ事をしたのがガロアです。
中学で習った2次方程式にはもちろん根の公式があるわけですから、
2次方程式は代数的に解けることになります。
従って、3次方程式が与えられたとき、もしその3次方程式を2次方程式に帰着させることが
できれば解くことができます。
4次方程式も3次方程式に帰着することで解けますが、
実はこのように次数を下げて根の公式を作れるのは4次までなのです。
5次方程式になるとどんなに工夫をしても次数を下げることはおろか、
逆に次数が5次より大きくなってしまいます。
6次方程式になるともっと悲惨なことが起きてくるわけです。
多くの人々が5次以上の方程式を代数的に解こうとしましたが成功しませんでした。
そのように1800年位までは4次までが代数的に解きうるとされていたのです。
そこで発想を転換しておそらく5次以上の代数方程式には根の公式が存在しないので
はと考え出した人が現れだしました。
しかしながらそれを証明することはそれほど容易なことではなく、成功したのはたったの2人でした。
アーベルは代数方程式の根になる数がどのような性質を持つのかを調べ体の概念を発
見します。体の定義を厳密に書いておきましょう。
(定義)
集合Fが体であるとは、F≠φであって、Fには足し算(+)と掛け算が与えられてい
て次の9つの公理を満たすものを言う。
- a+(b+c)=(a+b)+c
- Fの中には0が存在してa+0=0+a=aを満たす。
- a+b=b+a
- Fの中にはa+x=0を満たすxが存在してこのxを-aと書く。
- a(bc)=(ab)c
- ab=ba
- a(b+c)=ab+ac
- Fの中には1が存在してa1=1a=aを満たす。
- Fの0でない任意の元aはax=1を満たすxをFの中にもつ。このxをa‐と書く。
(ただし∀a,b,c∈F)
実は体にはいろいろな定義の仕方がありますが、上の定義の仕方が最も純粋でしょう。
すぐにわかることですが実数や複素数(高校でやりますよね)それから有理数などは全て体です。
もちろん体の例はこれだけではありません。
数学の中には実に多くの体が現れます。
ここでアーベルはこの体を用いて代数方程式を代数的に解くということを翻訳しようとします。
一般的な定義に入る前に我々も考えてみましょう。
よく知っている2次方程式で考えてみましょう。
まずは全ての係数が有理数であることを仮定しましょう。
最初に2次方程式が実数解を持つ場合ですが、有理数全体をQで表します。
(これは定義から体です)
そして判別式(これはどうでしょう?中学ではやるのかな?)
をDで書くことにしましょう。(係数が有理数なのでDも有理数)
2次方程式の根の公式には が現れますがこれは有理数とは限りません。
が現れますがこれは有理数とは限りません。
そこで数学の自由さを存分に発揮して、Qと を含む新しい体を作ってやりましょう。
それをQ(
を含む新しい体を作ってやりましょう。
それをQ( )と表して、
Qに
)と表して、
Qに を添加した体と呼ぶことにしませんか。
Q(
を添加した体と呼ぶことにしませんか。
Q( )は
)は
 =0のときはQと一致しているのでこのときは体です。
=0のときはQと一致しているのでこのときは体です。
 ≠0のときはその逆数を取れば
≠0のときはその逆数を取れば
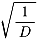 となり1/Dは方程式の係数を有理数に限定してあるのでやはり有理数です。
よって
となり1/Dは方程式の係数を有理数に限定してあるのでやはり有理数です。
よって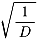 ∈Q(
∈Q( )となり
かつ
)となり
かつ と掛けて1になりますから、
Q(
と掛けて1になりますから、
Q( )の0でない元はすべて体の定義の9を満たします。
(1〜8を満たすことは自明でしょう)
このことからQ(
)の0でない元はすべて体の定義の9を満たします。
(1〜8を満たすことは自明でしょう)
このことからQ( )はQに
)はQに を添加した「体」と言ってもよいでしょう。
を添加した「体」と言ってもよいでしょう。
さてよくよく考えてみると2次方程式の全ての根はQ( )に含まれていて、Q⊂Q
(
)に含まれていて、Q⊂Q
( )なる包含関係が成り立つこともわかります。
(もちろん今は2次方程式が実数解を持つ場合ですが)
Q(
)なる包含関係が成り立つこともわかります。
(もちろん今は2次方程式が実数解を持つ場合ですが)
Q( )のことをQの拡大体と言います。
(QをQ(
)のことをQの拡大体と言います。
(QをQ( )の部分体と言います)
)の部分体と言います)
ここまでくると次の疑問が浮かんでくるかもしれません。
「2次方程式が実数解を持つのならば、初めからQではなく実数全体を持ってくればい
いじゃないか」
なるほど、確かに初めから実数全体(これをRで書きましょう)で考えていれば実数
解を持つ以上全ての2次方程式の根はRの中にあるのはあたりまえです。
結論から言ってしまえば2次方程式が虚数解を持つ場合にQではなくRを持ってくる必要があるのです。
さあ、それでは2次方程式が虚数解を持つ場合を考えてみましょう。
その場合判別式の値は負になりますので、2乗して-1になる数を作る必要があるわけですが、
その辺の詳しい事情は高校の教科書に譲るとしましょう。
さて、虚数というのは複素数の中にあるので複素数全体をCで書きましょう。
定義からこれもやはり体になるのです。
しかもRと比べて比較にならないほど多くの数を含んでいます。
つまりR⊂Cが成り立つことになります。
またCの任意の元はa+biと言う顔をしています。
(ただしa,b∈R、i(アイ)は虚数単位)ここでRにiを添加したR(i)を考えてみましょう。
これは体になることは自明でしょう。
そしてR⊂R(i)が成り立ちます。
ところでR(i)は体なので積について閉じていますからbi∈R(i)であって、
和についても閉じています。
よってa+bi∈R(i)となります。
すなわちa,bは任意の実数ですからR(i)の元は全てa+biという顔をしていることがわかります。
(ここの所は多少厳密でないかもしれません)つまりR(i)=Cがわかりました。
このことから2次方程式が虚数解を持つ場合、R⊂R(i)=Cなる体の拡大を用意すればあらゆ
る2次方程式(係数も何でもよい)の全ての根(実根でも虚根でも)はR(i)=C
に含まれることがわかります。
実はCは代数的閉体と呼ばれ、数の中では最も広い体系をもち、2次といわず、
任意の次数の全ての方程式の根がCに含まれてしまうのです。
しかしながら今は方程式を代数的に、つまり4則演算と冪を何回も取ることで解
くことを話題としているので、Q⊂Q( )の拡大へ戻って進めていきましょう。
)の拡大へ戻って進めていきましょう。
さて、少し窮屈に感じるところは2次方程式の係数を有理数に制限しているところです。
この条件を取り去るにはどうしたらよいでしょうか?
任意係数の2次方程式を用意して、その係数を降冪の順にa,b,cとします。
(つまりaはxの2乗の係数、bはxの係数、cは定数項)
ここで、次の体を作ってみたらどうでしょう。
つまりQ(a,b,c, )
)
a,b,cは有理数とは限らないのでQ(a,b,c, )は
Q(
)は
Q( )の拡大体となり
2次方程式の根の公式と言うのはその係数と
)の拡大体となり
2次方程式の根の公式と言うのはその係数と で構成されているので、任意係数の2次方程
式の根は全てQ(a,b,c,
で構成されているので、任意係数の2次方程
式の根は全てQ(a,b,c, )に属していることになります。
)に属していることになります。
従って2次方程式の場合はQ( )⊂Q(a,b,c,
)⊂Q(a,b,c, )なる体の拡大を
作ってやれば全ての根が拡大しきった体Q(a,b,c,
)なる体の拡大を
作ってやれば全ての根が拡大しきった体Q(a,b,c, )の中に入る事がわかりました。
)の中に入る事がわかりました。
3次方程式や、4次方程式の場合もQにその係数と判別式にルートを取ったものを添加した体を
作ってやれば全ての根がその体の中に入ることがわかります。
そうすると、方程式が代数的に解ける
ということはQにその係数を全部添加した体(これをその方程式の定義体という)に
累乗根を次々と添加して体を拡大していくことによって全ての根を含む体を作ること
ができると言うことができます。
逆にいうと方程式が代数的に解けないとは全ての根
を含むような定義体の拡大体が作れないということです。

| NO.702
| 2000.1.1. | WAHEI | 代数方程式の代数的解法(2)
|
part 2
前回のNO.699 part1では気の赴くままに書いてしまい、
投稿の計画やどこまで語るかの方向性を書くのを忘れてしまいました。
part2ではこれから先進んでいくための多少の道具を用意しつつ
僕がなぜこれを書こうと思ったかの動機を(忘れなければ)書いていこうと思います。
まずは写像と言う概念です。高校では参考書には載っているのをたまに見かけます
が、写像は数学を組み立てていく上で決定的な役割を果たします。ここでその定義を
書いておきましょう。
(定義)
AとBをどちらもφでない集合とする。
A×B={(a,b)|a∈A、b∈B}としてこれをAとBの直積という。
さて、g:A → B が「AからBへの写像である」とは次の3つを満たすことをいう。
- g⊂A×B
- ∀a∈Aについて(a,b)∈gとなるbBが必ず存在して、
このbをg(a)とかいてaのgによる像という。
- (a,b)∈gかつ(a,b’)∈g⇒b=b’
注意すべきは3番目の条件でしょうか。
これを写像のwell-defined性といいます。
つまり出発点(aのこと)が固定されていれば行き着いた先(bのこと)も同じになっ
ていないといけないということです。
この定義は数学的過ぎてかえって混乱するかも
しれませんが、噛み砕いて言うと
「写像gとはAの各元についてBの元を対応させる規則である」ということです。
つぎは写像の種類について定義しておきましょう。
(定義)
g:A → Bが単射であるとは∀a,b∈Aについてg(a)=g(b)⇒a=bということ
g:A → Bが全射であるとは∀b∈Bについてb=g(a)となるaがA内に存在すること
g:A → Bが全単射であるとはgが全射かつ単射であるということ
gが単射ならば定義からg(a)≠g(b) ならばa≠bということですからつまりAの元とB
の元が1つ1つ対応しているということがわかります。
またgが全射ならばBの全ての元はAからやってくる、
つまりBの元は根元(a∈Aのこと)を持つというように解釈できます。
最後にgが全単射の場合を考察しておきましょう。
定義からgは1つ1つ、かつ残りなく対応しているということですので、
実はgが全単射ならばAの元の個数とBの元の個数が等しいということが言えます。
NO.699 part1ではアーベルが体を用いて代数方程式の構造を調べたと言うことを書きました。
なぜこんな写像と言うものを定義したのかピンとこないかもしれません。
しかしある種の写像が全単射であればその写像によって結ばれた2つの集合が数学的に
(見掛けは違っていても)全く同等の構造をもつと見なせるのです。
NO.699 part1で5次以上の方程式には根の公式がないことを証明したのは2人いると述べました。
一人はアーベルですが、もう1人はガロアという人です。
ガロアはアーベルが見つけた体をそれよりももっと単純な構造をもつ
「群」という集合に置き換えて方程式の謎を解明しました。
そのときガロアが考え出したアイデアが体と群との間に全単射な写像を定めることだったのです。
しかしながら、そのアイデアはあまりにも時代を先行しすぎていて
当時(1830年ごろ)の人々には全く理解されませんでした。
part3ではこの群の定義をして5次以上の代数方程式には根の公式が存在しないとい
うアーベルの定理を紹介したいと思います。
そうそう、僕が投稿しようと思ったきっかけはコロキウム室が大変面白かったこと
と、そのコロキウム室に寄せられている話題がどちらかといえば解析系であるなと
思ったからです。またアーベルの定理について何気なく触れられているものの、やは
り方程式を解析的に近似を用いて解いているのを見かけました。
方程式を代数的に解くということがどれだけ深い数学を必要とするか、
他の読者の人々にも漠然とでもいいので理解されれば、
僕の意図は相当程度達成されたことになります。

| NO.704
| 2000.1.1. | WAHEI | 代数方程式の代数的解法(3)
|
part 3
NO.699 part1ではアーベルのアイデア
(方程式が代数的に解けるとは全ての根を含むような
定義体の拡大の列が作れる)をざっと紹介しました。
part3ではまず群を定義して、ガロアのアイデアを述べてみたいと思います。
その後に数学(もちろん高校数学も含
みますが)を根底から支えている、ある3つの公理を紹介したいと思います。
さてと、群ですが、これはもともとコーシーという数学屋さんが作った(らしいので
すが)ものですがコーシーが考えていたのは無限集合であって、有限集合で群を打ち
立てたのは本質的にガロアです。
驚くことですがガロアはこのアイデアを牢獄の中で思いついたらしいのです。
(定義)
集合Gが群であるとは、G≠φであって、Gには1つの演算(掛け算と同じ表し方をし
ましょう)が与えられていて次の3つを満たすものをいう。
- a(bc)=(ab)c
- Gの中には∀a∈Gに対してae=ea=aなる元eが存在する。このeをGの単位元という。
- ∀a∈Gに対してax=xa=eなるxがG内に存在する。このxをaの逆元といいa‐と書く。
この定義も体のときと同様、何やら普通の数と似ています。
しかし1つだけ腑に落ちないところは可換性を仮定していません。
つまりab=baが成り立たなくても上の定義さえ満たしていればその集合を群というのです。
なぜ、可換性を一般に仮定しないのでしょうか?
いろいろ叫ばれているところですが、歴史的に見ると群とは2つの合同
な正多角形を重ね合わせる際に現れる現象を数学的に記述したもので、そのためか数
の一般化という意識が低く、可換性を仮定し忘れたとも言われています。
考えてみれば図形の張り合わせ方をベースにして上のような一般的な定義にするというのは大変
な努力が費やされたに違いありません。
その意味では現代に生まれている我々は先人の努力に対して謙虚にならなければならないでしょう。
脱線してしまいましたが、それにしても実際問題として可換性がないと不便でどうし
ようもありません。そこで、群がab=baを満たすということも仮定しておきましょ
う。(特にそのような群をアーベル群といいます)
さてアーベル群の例を調べておきましょう。演算を普通の数の足し算としてみると整
数全体(Zで書きます)はアーベル群です。なぜならば、まずZから勝手に2つの元を
取ってきます。(元とかいうふうに物々しく書いていますが要するに2つの整数を
取ってくると言うことです)それをa,bで書きましょう。するとa+bはもちろん整数
で従ってZの元です。よってZには数の足し算が演算として与えられていることがわか
ります。またa+(b+c)=(a+b)+cは整数の世界では常に成り立っていますので定義の1
もOKです。さて0は整数です。(0は自然数ではありません)そしてよく知られてい
るように∀a∈Zに対してa+0=0+a=aが成り立ちます。よって定義の2もOKでZでは数の
足し算においては0が単位元ということですね。そして3番目ですが、a∈Z⇒-a∈Z
ですので両者をたすと0となり以上のことからZは数の足し算でアーベル群です。
ところがZは数の掛け算では群になりません。惜しいことに定義の3を満たさないの
です。掛け算の場合(それがZの演算になっていることは明らかでしょう)単位元は
数の1です。しかしax=1となるxは整数に入っているとは限りませんからね。
(例としてはa=2とするとx=1/2となり1/2は整数ではありません)
でもZは数の足し算でアーベル群ですので、Q(有理数)もR(実数)もC(複素数)も
足し算でアーベル群であるということが予想されます。これは実に自然な予想で正し
い予想です。まとめてみると・・・
- 群は可換性を必ずしも仮定しないが、もし仮定すると数によく似た性質を持つ
- Zは数の足し算でアーベル群
- QとR、それからCも数の足し算でアーベル群となる
- Q、R、Cは数の掛け算でも実はアーベル群となる
(3)と(4)に分配法則、つまりa(b+c)=ab+ac を付け加えるとQ、R、Cは数の足し
算と掛け算で体になっているということです。(これを体の定義にしてもよかったか
なと思いましたが、結局やめました)次に純粋な群の例を身近な例で挙げてみましょ
う。行列はどうでしょう?ただしこの場合は演算は行列の足し算と掛け算にしましょ
う。(たしか高校の教科書では数学Cに入っていましたね)m行n列の行列の全体を
M(m、n)で書くことにすれば、これはZのときと同じようにして群であることが
示されますが、行列では可換性は成り立ちませんでした。従ってM(m、n)はアー
ベル群ではありません。(行列の成分は最も広い複素数としておきましょう)ちなみ
にM(m,n)において行列の掛け算での単位元は対角成分が全て1で残りが0の行
列、つまり単位行列で、行列の足し算での単位元は全ての成分が0の行列です。僕が
思うに行列は最も純正でクラシカルな群であると思います。
当面の目標はこの群と体を準同型写像を用いて結びつける事をします。
(定義)
AとBを共に体とする。g:A → Bが準同型写像であるとは、gは写像で次の3つを
満たすことをいう。
- g(a+b)=g(a)+g(b)
- g(ab)=g(a)g(b)
- g(1)=1
(ただし3において左辺の1はAの1、右辺の1はBの1)
この定義が言っていることを吟味してみましょう。今のところ知っていることは体の
定義と写像の定義だけです。Aは体ですからAには2つの演算、足し算と掛け算(必
ずしも数のそれとは限らない)が与えられています。g(a+b)はaとbをAの中で足
してgでBへ送っていると言うことです。またg(a)+g(b)はAの元aとbをgでBへ送
る、写像の定義からそれらはg(a),g(b)という顔をしていてBの元であり、Bは体な
ので足し算があるからg(a)とg(b)をBの中で足しているということでしょう。その両
者が等しいというのが1番目の主張です。2番目の条件は掛け算で同じことができる
と言うことでしょう。3番目は1は1へ移るということでしょう。この定義は一体何
を言っているのでしょう?体の定義を思い出してください。大前提は演算が与えられ
ていることでした。演算がなければ何もできません。従って体の「構造」を成す物は
演算といってよいでしょう。上の定義で1番目と2番目の条件は演算が演算に移る、
つまり準同型写像と言うものによって2つの体の構造が保持されるということです。
実はこのことから3番目の条件は不要である、つまり、条件の1,2と体の定義から
3番目は自動的に出てくることがわかります。(確かめてみてください)
また、もし準同型写像が全単射のとき、その写像を同型写像といい、結ばれる2つの
体はお互いの構造を保持し、かつ元の個数が等しいということなので(NO.702 part2参照)
見かけは違っていても数学的には同じ集合と見なしてよいのです。同型写像で結ばれ
た2つの集合はお互いに同型であると言います。方程式の定義体とある群を同型写像
を用いて結びつけることがガロア理論の真髄と言えるかもしれません。
(数学を根底から支える重要な3つの公理について)
その名前は
- Zornの補題(Zorn's lemma)
- 整列定理(well-ordering-threorem)
- 選択公理(axiom of choice)
といいますが、これらについてはまた新しい用語の定義を必要としますので、part5
辺りに回したいと思います。
それからアーベルの定理はpart4で書くことにしましょう。
(上の3つが互いに同値であることは証明されています。
しかしながら個々の証明は出来ない、あるいは証明しないで認めてよいとされているようです)
またガロアのアイデアもpart4でまとめて書きます。ごめんなさい。

| NO.706
| 2000.1.2. | WAHEI | 代数方程式の代数的解法(4)
|
part 4
まずは写像の合成を説明しておきましょう。
f をAからBへの写像、g をBからCへの写像としましょう。
∀a∈Aをf でBへ移します。
するとf(a)∈Bですが、今度はこのf(a)をgでCへ移します。
つまりg(f(a))∈Cとなります。
このg(f(a))を(gf)(a)と書くこと
にして、(gf)を写像f とg の合成といいます。
(gf)は明らかにAからCへの写像となります。
2つの写像において集合Bが共通していることに注目してください。
電車でいえばこのBが連結器の役割をしているといえましょう。
帰納的に(ドミノのように)何個かの集合がありそれぞれの間に少なくとも
1つの写像が定められていればそれぞれを合成して最初の集合と最後の集合の間に
1つの新しい写像を定めることが出来ます。
ここで、ある重要な群の例を紹介しておきましょう。
(対称群)
Xをφでない集合としましょう。
そしてXとXの間に写像を定めてやればそれが全単射
になるようにできるはずです。
というのもXからX、つまり自分自身への写像ですか
ら、当然元の個数だって等しいはずなのでうまく対応をつけてやれば全単射にするこ
とが出来るでしょう。
このとき(写像が全単射のとき)逆写像を定めることが出来ます。
fをXからXへの全単射としましょう。
∀a∈Xを取ってb=f(a)とおきます。
fの逆写像とはこのbに対してaを対応させるものです。
つまりfの逆写像をf‐でかけば、
上のb=f(a)をf‐でXへ移すと
f‐(b)=f‐(f(a))=a
となるということです。
ここで次の集合を考えましょう。
S(X)={f|fはXからXへの全単射}
この集合は数の集合ではありません。
そのへんが多少抽象的でわかりにくいと思いますが、S(X)は写像の集合です。
簡単のため、X={1,2,3}として考えてみましょう。
いま写像fは{1,2,3}から{1,2,3}への全単射な写像です。
このときS(X)を具体的に書き出すことを考えてみましょう。
まず1を1へ、2を2へ、3を3へ移す写像がありますよね。
つまりXのすべての元を固定する写像です。
(この写像を恒等写像といいます)
これを(1 → 1、2 → 2、3 → 3)と表すことにしましょう。
次に考えられるのは1を固定して2を3へ、3を2へ移す写像があります。
これを同じように(1 → 1、2 → 3、3 → 2)と書きましょう。
さて次はどうすればいいのかな。前の2つの写像では1の行き着いた先が1でした。
(つまり1が固定)そこで今度は1の行き着いた先を2にして考えてみましょう。
すると(1 → 2、2 → 3、3 → 1)と
(1 → 2、2 → 1、3 → 3)の2つが考えられます。
ではつぎは1の行き着いた先を3にして考えてみればよさそうです。
このときは(1 → 3、2 → 1、3 → 2)と(1 → 3、2 → 2、3 → 1)となります。
これで全部でしょうかね・・・・・うん、全部です。
よってS(X)は今書き出した6つの元で構成されています。
さて、S(X)から2つの元f、gを取ってきましょう。
S(X)の定義からこの2の写像は
全単射ですが、その合成(gf)を考えてみましょう。
fもgも全単射なのでその合成も全単射なのではと予想できますが、実際に証明してみましょう。
示すべきは(gf)が単射かつ全射ということです。
∀a、b∈Xについて
(gf)(a)=(gf)(b)とすると合成の定義からg(f(a))=g(f(b))となりg は全単射なので単
射、従ってf(a)=f(b)よってfはやはり単射だからa=bとなり(gf) は単射。
また、∀c∈Xに対してgが全射なのでg(d)=cとなるdが存在し、さらにfが全射なのでdに対
しd=f(e)なるeが存在している。
よって(gf)は全射でもある。
以上のことからf,gが全単射なら(gf)も全単射であることがわかりました。つまり(gf)∈S(X)です。
また恒等写像はS(X)内に必ず存在していますので、S(X)≠φです。
ところで、AからBへの2つの写像f,gが与えられたとき写像が等しいということ、
つまりf=gを∀a∈Aに対してg(a)=f(a)で定義しましょう。すると
(f(gh))(a)=f(gh(a))=f(g(h(a)))
((fg)h)(a)=(fg)(h(a))=f(g(h(a))) (∀f,g,h∈S(X), ∀a∈X)
ですから、f(gh)=(fg)hがS(X)内で成立しています。
また恒等写像を1で書くことに
すると(これは数の1とは違います。写像です)
∀a∈Xについて
1(a)=aですから(恒等写像は全ての元を固定するので)
(f1)(a)=f(1(a))=f(a)
(1f)(a)=1(f(a))=f(a)
となり、1f=f1=fが成り立ちます。
また∀f∈S(X)は全単射なので逆写像があり、
その定義から(ff‐)(a)=1(a)、(f‐f)(a)=1(a)ですので、
ff‐=f‐f=1が成り立ちます。
ここまでで不思議なことがわかりました。
すなわちS(X)は写像の合成を演算にして群になるのです。
NO.704 part3では群は数や行列と似ていると書きましたが、ここでその数の
領域を1歩踏み出したことになります。
つまり演算とは必ずしも数や行列の演算ばかりではないということです。
また群の例も実に多種多様であることを予感させます。
(さらにS(X)は元の個数が有限な群、有限群であることにも注目してください)
こういうところに数学の自由さを感じるのは僕だけでしょうか?
とにかく、S(X)は写像の合成を演算にして群を成し、S(X)のことをX上の対称群といいます。
特にX={1,2,3、・・・・n}としたときのS(X)をn次対称群といいます。
しかるに、例で説明したX={1,2,3}の場合はS(X)は3次の対称群です。
ところで3次の場合その元の個数は6個、つまり3!個です。
この事は一般化できて、実はn次対称群の元の個数はn!個です。
高校では順列というのやると思います。n個の物を並べ替える方法は確かn!通りありました。
これはS(X)の元の個数にほかなりません。
つまり(3次対称群のところで気が付いたかもしれませんが)S(X)の元を1
つ取ってくることと、1からnまでの順列を1つ定めることは同値なのです。
(同値とは同じ事という意味です)
対称群の説明がだいぶ長くなってしまいました。
ガロアはNO.699 part1で説明した
方程式の根を含む体の拡大列とこの対称群とを
NO.704 part3で説明した同型写像で結びつけることに成功しました。
(もちろん当時はまだまだ数学が創世記にあったため、ガロア自身今とはだいぶ違う表現をしていますが)
ここで部分群について説明しておかなければいけません。
(定義)
Gを群とする。H⊆GがGの部分群であるとはH≠φであって、∀a,b∈H⇒ab-∈Hであ
ることをいう。
実に簡単な定義ですが、数学ではたいていの群が何か大きい群の部分群として現れる
ので、この定義は重要です。
注意してほしいのはa,bをHから取ってきたら、ab∈Hではなくて、
ab‐∈H(aとbの逆元の積)を定義としてあるところです。
この定義さえ満たせば、HはGの演算で群になります。
(つまり群の定義を満たします)これはぜひ確かめてみてください。
牢屋のなかで、ガロアは実に画期的なことを考えます。
S(X)において、Xをn次方程式の根を含む体とし、S(X)の元を同型写像として考えます。
そのときのS(X)を体上の自己同型群といい、AutXと書きます。
(AutXが群になることは証明したので認めてよいでしょう)
そのときこのAutXの部分群とXの中間体(体拡大の列に含まれ
る体で拡大しきった体Xと最小の体も中間体とする)との間に全単射な写像を定めら
れることを、ガロアは示しました。
これはすごいことを言っています。つまり、もし
AutXが有限群ならば、その部分群はもちろん有限個しかないわけでその部分群た
ちと、体拡大の中間体が1つずつ、しかも残りなく対応しているというのですから、
AutXが有限群である以上、それに対応している中間体も有限個しかないというこ
とになります。もっというと例えばAutXの部分群が8個あれば、それに対する中
間体も8個あるということです。ここで、Hを群Gの部分群とすると、{e}とG自
身もGの部分群になっていることは定義から明らかでしょう。ただし{e}は単位元
だけからなるGの部分集合です。
ガロア理論(ガロアが牢屋の中で考えた理論)の本質は上に述べたことです。すなわ
ち、体上自己同型群の部分群と体拡大の中間体の間に全単射が存在する。
(アーベルの考えた事との関係)
5次以上の方程式には根の公式がないというのがアーベルの定理です。
言葉で書いて
しまえばこれだけのことですが、体の概念がなく、群もいわゆる無限群しかなかった
時代にアーベルとガロアは時代を先行しすぎていたことは否めないでしょう。
アーベルの定理の証明は基本的に背理法です。(高校でやるかと思います)つまり、
5次以上の方程式が根の公式を持ったとします。するとその方程式は代数的に解ける
ことになりますのでうまく全ての根を含む定義体の拡大体を作れることになります
が、この議論を進めていくと明らかな矛盾が生じることになるのです。(いまは全て
の体をCの部分体としましょう)
しかし、この証明を完全な形で述べるにはまだまだ
準備不足で、ここでは到底述べることはできません。不本意ですが、この詳しい証明
はあとで時間が許せばやりたいと思います。
ガロアの理論によると、このアーベルの定理を群の言葉を使って翻訳できるというこ
とです。群のほうが体よりは単純な構造を持ちますので、群の言葉を使ってアーベル
の定理を表現した方がわかりやすいと思うかもしれません。しかし数学のみならず、
理論の世界では単純化するのが結構難しい場合もあります。この例も恐らくそうかも
しれません。
実は本当に申し訳ないことに群の言葉を使ったアーベルの定理はまだ準
備不足のためやはり述べられません。ざっと、準備すべきものを挙げるとすれば、同
値関係、正規部分群、可解群、ガロア群などを挙げることができます。しかし、これ
らの概念は正直に言えば、わかりやすく書くことが非常に困難であり、方程式を代数
的に解くことの数学的雰囲気を味わってもらうためには必ずしも必要でない記述をし
なければなりませんから、これ以上深入りしないことにします。
さて、いろいろと不備があるかもしれませんが、なんとかガロア理論の入り口までた
どり着けました。大急ぎでたどり着いた感がありますので、忘れ物が多いですが、後
で補うべきところをじっくり考えて、次回以降に付け足します。

| NO.707
| 2000.1.3. | Junko | 代数方程式の代数的解法(5)
|
NO.706 part4にある
(定義)
Gを群とする。H⊆GがGの部分群であるとはH≠φであって、∀a,b∈H⇒ab-∈Hであ
ることをいう。
について考えてみます。
2.単位元について
∀a∈Hについて、aa−∈H、つまり e∈H
3.逆元の存在について
e∈Hですから、∀a∈Hについて、ea−∈H、つまり a−∈H
1.結合律について
∀a,b∈Hについて、b−∈Hなので、
a(b−)−∈H、つまり ab∈H
従って、集合Hはこの演算について閉じていることになります。
集合Hはもちろん集合Gの部分集合ですから、結合律が成り立ちます。
従って、Hは群をなすことがわかります。
逆はもちろんです。

次へ
 戻る
戻る
 が現れますがこれは有理数とは限りません。
が現れますがこれは有理数とは限りません。 を含む新しい体を作ってやりましょう。
それをQ(
を含む新しい体を作ってやりましょう。
それをQ( )と表して、
Qに
)と表して、
Qに を添加した体と呼ぶことにしませんか。
Q(
を添加した体と呼ぶことにしませんか。
Q( )は
)は
 =0のときはQと一致しているのでこのときは体です。
=0のときはQと一致しているのでこのときは体です。 ≠0のときはその逆数を取れば
≠0のときはその逆数を取れば
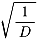 となり1/Dは方程式の係数を有理数に限定してあるのでやはり有理数です。
よって
となり1/Dは方程式の係数を有理数に限定してあるのでやはり有理数です。
よって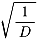 ∈Q(
∈Q( )となり
かつ
)となり
かつ と掛けて1になりますから、
Q(
と掛けて1になりますから、
Q( )の0でない元はすべて体の定義の9を満たします。
(1〜8を満たすことは自明でしょう)
このことからQ(
)の0でない元はすべて体の定義の9を満たします。
(1〜8を満たすことは自明でしょう)
このことからQ( )はQに
)はQに を添加した「体」と言ってもよいでしょう。
を添加した「体」と言ってもよいでしょう。 )に含まれていて、Q⊂Q
(
)に含まれていて、Q⊂Q
( )なる包含関係が成り立つこともわかります。
(もちろん今は2次方程式が実数解を持つ場合ですが)
Q(
)なる包含関係が成り立つこともわかります。
(もちろん今は2次方程式が実数解を持つ場合ですが)
Q( )のことをQの拡大体と言います。
(QをQ(
)のことをQの拡大体と言います。
(QをQ( )の部分体と言います)
)の部分体と言います) )の拡大へ戻って進めていきましょう。
)の拡大へ戻って進めていきましょう。 )
) )は
Q(
)は
Q( )の拡大体となり
2次方程式の根の公式と言うのはその係数と
)の拡大体となり
2次方程式の根の公式と言うのはその係数と で構成されているので、任意係数の2次方程
式の根は全てQ(a,b,c,
で構成されているので、任意係数の2次方程
式の根は全てQ(a,b,c, )に属していることになります。
)に属していることになります。 )⊂Q(a,b,c,
)⊂Q(a,b,c, )なる体の拡大を
作ってやれば全ての根が拡大しきった体Q(a,b,c,
)なる体の拡大を
作ってやれば全ての根が拡大しきった体Q(a,b,c, )の中に入る事がわかりました。
)の中に入る事がわかりました。

 戻る
戻る