Weekend Mathematics/コロキウム室/1999.10〜12/NO.79
コロキウム室
| NO.691
| '99 12/16 | sambaGREEN | 新聞紙の折り曲げ(4)
|
私も,件のテレビを見た記憶がかすかにあります。
体育館いっぱいに紙を広げて(実際にはそんな大きな紙はないので,つなぎ合わせて)
小学生が,一所懸命挑戦していました。
高さは,NO.687で「浜田さん」が計算されているように,文字通り,幾何級数的に増加します。
実際に折るときに問題になるのは,紙の大きさです。
新聞紙の体積は一定ですから,厚み(高さ)がk倍になると,面積はk分の1になります。
1: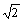 の紙で考えると,2回おる毎に長辺が半分になります。
の紙で考えると,2回おる毎に長辺が半分になります。
「浜田さん」が限度と考えておられる10cmで考えると,8回折ったとき厚みは5cmです。
今,折り曲げて高さが10cmにするには40cmの長さが必要と仮定すると(まあ妥当な線?),
もとの紙の長辺は40cm×24=640cm(6.4m)必要になります。
実際に,新聞紙を折ってみたところ,7回折れて,厚みは約1cmが限界でした。
「浜田さん」の計算結果からは,約2.5cmになるはずですから,
実際の新聞紙の厚みは,0.1mm弱しかないようです。
したがって,高さ10cmの状態は,
長辺が約9m(6.4×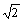 )の紙で10回折った状態と言うことになります。
)の紙で10回折った状態と言うことになります。
もし,20回折りたければ,どのくらいの紙を用意すればよいか考えてみます。
計算を簡単にするため,紙の厚さを0.1mmとします。
高さは,0.1mm×10002=100000mm=100m この状態にするには長辺は400m必要。
もとの用紙の長辺は 約1000倍必要
(正確には512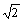 ですが,400mの設定もaboutなので)。
ですが,400mの設定もaboutなので)。
400m×1000=400km とんでもない数字がでてしまいました。
新聞紙を100回折った厚みも文字通り天文学的数になりますが,
更に驚くべきは,実際に100回折るために用意しなければならない紙の大きさでした。
概算で,その長辺は,k×1038km。
(kは折り曲げ限界の高さと長辺の設定による。まあ,大した問題ではないですね。ここまでくると)

| NO.692
| '99 12/16 | Junko | 新聞紙の折り曲げ(5)
|
y=ax (a>0,a≠1)という形をしているものを指数関数といいます。
それに対して、y=xnという形をしているものを整関数といいます。
整関数がどんなにがんばっても(どんなに次数をあげても)、指数関数にはかないません。
それを示すのがこの式です。a>1として、
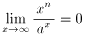
この極限値はロピタルの定理を適用すればわかります。
分母分子を別々に微分していったときに、分子にある整関数はどんなに次数を高くしても有限である限り、
いずれ有限回で定数になります。
一方、分母にある指数関数は微分するたびにlog aという定数がつきますが
基本的にaxのままです。
グラフをかいてみると、整関数の方が優勢のように見えますが、いずれ必ず指数関数に抜かれます。
整関数と指数関数とでは次元が違う? いやいや次元を超越している?
試しに、底が2の指数関数 y=2x と4次関数 y=x4 で見てみます。
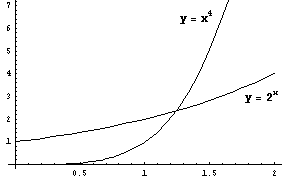
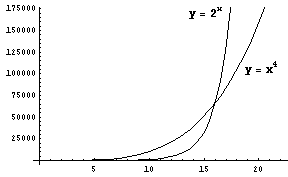
x=1.23・・・あたりで交差したあとは4次関数 y=x4が優勢ですが、
x=16で指数関数 y=2xが再逆転します。

| NO.693
| '99 12/16 | kiyo | サンタの贈り物(2)
|
幸運な10桁の数は3816547290の1個だけです。
解答になりませんが。

| NO.694
| '99 12/16 | 水の流れ | ISBNコード
|
博識ある読者の皆さん、教えてください。
<「分数ができない大学生」:岡部恒治等:東京経済新報社>という本に中に、
こんな一文がありました。
「すべての書籍についてISBNコードは、表示されている10個の数字にそれぞれ左から、
1,2,3,・・・、10を書けて、それらの10個の結果の合計を求めると必ず11の倍数になる。
ただし、Xは10と考える。
このISBNコードは、一字だけ誤って読んだときはその誤りが認識できる、
それに関しては11が素数であることが本質な役割をしている。」
質問1:太郎さんが始めて知る、このISBNコードとは何のこと。
また、どんな役割があるの。
質問2:文中にでてくる計算をすると、どうして11の倍数になるの。
質問3:文中にでてくる、1字だけ誤って読んだとき、その誤りをどうして認識できるの。
以上ですが、よろしくお願いします。

| NO.695
| '99 12/17 | ふじけん | サンタの贈り物(3)
|
10桁の数字を
[1][2][3][4][5][6][7][8][9][10]
とします。
まず、[1][2][3][4][5][6][7][8][9][10]は10の倍数なので [10]=0。
[1][2][3][4][5]は5の倍数で0は使っているので [5]=5。
[1][2],[1][2][3][4],[1][2][3][4][5][6],[1][2][3][4][5][6][7][8]は、
それぞれ偶数の倍数となるので[2],[4],[6],[8]には
2,4,6,8のいずれかが入る。
よって残りの[1],[3],[7],[9]には1,3,7,9のいずれかが入る。
ここで、[4],[8]に注目すると
[1][2][3][4]が[4]の倍数になるためには[3][4]が4の倍数になればよい。
ここで[3]は奇数なので[4]=2or6となる。
([3]×10≡2(mod4)より)
同様に[1][2][3][4][5][6][7][8]が8の倍数になるためには[6][7][8]が
8の倍数になればよい。
[6]が偶数なので[7][8]=16or32or72or96となる。
([6]×100≡0(mod8)、[7]≠5より)
よって[4],[8]=2or6、[2],[6]=4or8となる。
次に[6]に注目する。
[1][2][3]が3の倍数であることから[1]+[2]+[3]≡0(mod3)となる。
よって[1][2][3][4][5][6]が6の倍数であることから
[4]+[5]+[6]≡0(mod3)となり [5]=5なので
[4]+[6]≡1(mod3)となる。
[4],[8]=2or6、[2],[6]=4or8より([4],[6])=(2,8),(6,4)が決まり
その決まり方によって[2],[8]も決まる。
ここまでで10桁の数字は
[1]4[3]258[7]6[9]0 と [1]8[3]654[7]2[9]0
の2つにしぼられた。
7の倍数は、下から3桁ごとに区切り奇数番目のものの和と偶数番目のものの
和の差が7の倍数になることから
[1]4[3]258[7]6[9]0について考えると
[1]4[3]258[7]が7の倍数になるには
| [1]+(580+[7])−(402+10[3]) | ≡0(mod7)
|
| 178+[1]−10[3]+[7] | ≡0(mod7)
|
| [1]+4[3]+[7] | ≡4(mod7)
|
となればよく、
([1],[3],[7])=(1,7,3),(3,7,1),(3,9,7),(7,9,3)
が決まる。ここで、
- [8]=6より[7]=1or9
- [1]+[2]+[3]≡0(mod3)、[2]=4より [1]+[3]≡2(mod3)
という条件を考えると、この条件を満たす([1],[3],[7])は存在しないので
[1]4[3]258[7]6[9]0内には幸運な10桁の数字は存在しない。
同様に[1]8[3]654[7]2[9]0について考えると
| [1]+(540+[7])−(806+10[3]) | ≡0(mod7)
|
| −266+[1]−10[3]+[7] | ≡0(mod7)
|
| [1]+4[3]+[7] | ≡0(mod7)
|
([1],[3],[7])=(3,1,7),(7,1,3),(7,3,9),(9,3,7)
が決まる。ここで、
- [8]=2より[7]=3or7
- [1]+[2]+[3]≡0(mod3)、[2]=8より [1]+[3]≡1(mod3)
という条件を考えると、
([1],[3],[7])=(3,1,7) のみである。
また、1〜9の和が9の倍数であることから[9]に1〜9のどの数字を入れても
[1][2][3][4][5][6][7][8][9]は9の倍数となる。
∴幸運の10桁の数字は3816547290のみである。

第40回数学的な応募問題
太郎さんが勤務している学校には、何組かの双子がいます。
今、全部で2n人のn組の双子を一列に並べる方法は何通りあるか、知りたくなりました。
ただし、同じ組の双子は隣り合わないようにします。
そこで、次の問いに答えてください。
問題1:
n=1,2,3 のときの並び方は何通りあるか。
問題2:
一般に、a(n) 通りあったとして、漸化式を導いてください。
問題3:
可能なら、a(n) をnで表してください。
正直言って、まだ、太郎さんは一般の場合の答は知りません。

| NO.697
| '99 12/26 | 水の流れ | ミレニアム(1)
|
第41回数学的な応募問題
読者の皆さん!まもなく1000年代最後の年が終わります。そして迎える2000年。
百年どころか千年に一度の幕が下り、新たに2千年のいつもと違った特別な幕が上がります。
最近、ミレニアム(千年紀)というカタカナをよく耳にします。
そこで、問題です。
問題1:
A+happy+new−year=2000
ただし、A,h,a,p,y,n,e,w,rに異なる0から9までの整数を入れて、
式を成立させてください。
また、頭文字のA,h,y,n には0は入れないでください。
さらに、A,a には異なる数字が入ります。
※happy <==== 5桁の整数
new <==== 3桁の整数
year <==== 4桁の整数
問題2:
2000という数字について、次の問に答えてください。
(1)約数は何個ありますか。ただし、1と2000も含めてください。
(2)(1)の約数の和を求めてください。
(3)(1)の約数の逆数の和を求めてください。
(4)2000と互いに素な整数は何個ありますか。
(5)(4)の互いに素な整数の和を求めてください。
(6)幾つかの連続する自然数を加えて、ちょうど、2000にしてください。
(7)8個の異なる整数の立方和がちょうど、2000にしてください。
ただし、平成12年にちなんで、一番大きい整数は12とし、必ず使ってください。
また、一番小さい数は負の整数になっても構わないです。
問題3:
1から12までの自然数の平方数について、それぞれの和が等しいように、
2つのグループに分けてください。

| NO.698
| '99 12/28 | Junko | ミレニアム(2)
|
問題1
手作業で見つけました。
h=1でしょうね。a=0 か 2?
a=0、y=8 と見当をつけて、探していきました。
Aとwは交換可能ですので、一気に2つ。
| A | 答 4 | 5
|
| happy | 10338 | 10338
|
| new | 265 | 264
|
| -year | -8607 | -8607
|
| −−−− | −−−− | −−−−
|
| 2000 | 2000 | 2000
|
1(2?)組見つけたら満足・・・。
きっと他にもまだあると思うな・・・。

| NO.699
| '99 12/29 | WAHEI | 代数方程式の代数的解法(1)
|
part 1
もうすぐ2000年でいろいろな問題がとり立たされているようですけれど、さしあ
たって興味のある問題は代数方程式の代数的解法についてです。
大昔から4次方程式までは根の公式を用いて解けることが知られていました。
根の公式を用いて解くことを代数的に解くといいます。
いわゆる4則演算が定義されている集合を体といいますが、
この体を用いて代数方程式の構造を解明したのがアーベルであり、
演算が1つしか与えられていない集合である群を用いてアーベルと同じ事をしたのがガロアです。
中学で習った2次方程式にはもちろん根の公式があるわけですから、
2次方程式は代数的に解けることになります。
従って、3次方程式が与えられたとき、もしその3次方程式を2次方程式に帰着させることが
できれば解くことができます。
4次方程式も3次方程式に帰着することで解けますが、
実はこのように次数を下げて根の公式を作れるのは4次までなのです。
5次方程式になるとどんなに工夫をしても次数を下げることはおろか、
逆に次数が5次より大きくなってしまいます。
6次方程式になるともっと悲惨なことが起きてくるわけです。
多くの人々が5次以上の方程式を代数的に解こうとしましたが成功しませんでした。
そのように1800年位までは4次までが代数的に解きうるとされていたのです。
そこで発想を転換しておそらく5次以上の代数方程式には根の公式が存在しないので
はと考え出した人が現れだしました。
しかしながらそれを証明することはそれほど容易なことではなく、成功したのはたったの2人でした。
アーベルは代数方程式の根になる数がどのような性質を持つのかを調べ体の概念を発
見します。体の定義を厳密に書いておきましょう。
(定義)
集合Fが体であるとは、F≠φであって、Fには足し算(+)と掛け算が与えられてい
て次の9つの公理を満たすものを言う。
- a+(b+c)=(a+b)+c
- Fの中には0が存在してa+0=0+a=aを満たす。
- a+b=b+a
- Fの中にはa+x=0を満たすxが存在してこのxを-aと書く。
- a(bc)=(ab)c
- ab=ba
- a(b+c)=ab+ac
- Fの中には1が存在してa1=1a=aを満たす。
- Fの0でない任意の元aはax=1を満たすxをFの中にもつ。このxをa‐と書く。
(ただし∀a,b,c∈F)
実は体にはいろいろな定義の仕方がありますが、上の定義の仕方が最も純粋でしょう。
すぐにわかることですが実数や複素数(高校でやりますよね)それから有理数などは全て体です。
もちろん体の例はこれだけではありません。
数学の中には実に多くの体が現れます。
ここでアーベルはこの体を用いて代数方程式を代数的に解くということを翻訳しようとします。
一般的な定義に入る前に我々も考えてみましょう。
よく知っている2次方程式で考えてみましょう。
まずは全ての係数が有理数であることを仮定しましょう。
最初に2次方程式が実数解を持つ場合ですが、有理数全体をQで表します。
(これは定義から体です)
そして判別式(これはどうでしょう?中学ではやるのかな?)
をDで書くことにしましょう。(係数が有理数なのでDも有理数)
2次方程式の根の公式には が現れますがこれは有理数とは限りません。
が現れますがこれは有理数とは限りません。
そこで数学の自由さを存分に発揮して、Qと を含む新しい体を作ってやりましょう。
それをQ(
を含む新しい体を作ってやりましょう。
それをQ( )と表して、
Qに
)と表して、
Qに を添加した体と呼ぶことにしませんか。
Q(
を添加した体と呼ぶことにしませんか。
Q( )は
)は
 =0のときはQと一致しているのでこのときは体です。
=0のときはQと一致しているのでこのときは体です。
 ≠0のときはその逆数を取れば
≠0のときはその逆数を取れば
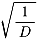 となり1/Dは方程式の係数を有理数に限定してあるのでやはり有理数です。
よって
となり1/Dは方程式の係数を有理数に限定してあるのでやはり有理数です。
よって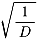 ∈Q(
∈Q( )となり
かつ
)となり
かつ と掛けて1になりますから、
Q(
と掛けて1になりますから、
Q( )の0でない元はすべて体の定義の9を満たします。
(1〜8を満たすことは自明でしょう)
このことからQ(
)の0でない元はすべて体の定義の9を満たします。
(1〜8を満たすことは自明でしょう)
このことからQ( )はQに
)はQに を添加した「体」と言ってもよいでしょう。
を添加した「体」と言ってもよいでしょう。
さてよくよく考えてみると2次方程式の全ての根はQ( )に含まれていて、Q⊂Q
(
)に含まれていて、Q⊂Q
( )なる包含関係が成り立つこともわかります。
(もちろん今は2次方程式が実数解を持つ場合ですが)
Q(
)なる包含関係が成り立つこともわかります。
(もちろん今は2次方程式が実数解を持つ場合ですが)
Q( )のことをQの拡大体と言います。
(QをQ(
)のことをQの拡大体と言います。
(QをQ( )の部分体と言います)
)の部分体と言います)
ここまでくると次の疑問が浮かんでくるかもしれません。
「2次方程式が実数解を持つのならば、初めからQではなく実数全体を持ってくればい
いじゃないか」
なるほど、確かに初めから実数全体(これをRで書きましょう)で考えていれば実数
解を持つ以上全ての2次方程式の根はRの中にあるのはあたりまえです。
結論から言ってしまえば2次方程式が虚数解を持つ場合にQではなくRを持ってくる必要があるのです。
さあ、それでは2次方程式が虚数解を持つ場合を考えてみましょう。
その場合判別式の値は負になりますので、2乗して-1になる数を作る必要があるわけですが、
その辺の詳しい事情は高校の教科書に譲るとしましょう。
さて、虚数というのは複素数の中にあるので複素数全体をCで書きましょう。
定義からこれもやはり体になるのです。
しかもRと比べて比較にならないほど多くの数を含んでいます。
つまりR⊂Cが成り立つことになります。
またCの任意の元はa+biと言う顔をしています。
(ただしa,b∈R、i(アイ)は虚数単位)ここでRにiを添加したR(i)を考えてみましょう。
これは体になることは自明でしょう。
そしてR⊂R(i)が成り立ちます。
ところでR(i)は体なので積について閉じていますからbi∈R(i)であって、
和についても閉じています。
よってa+bi∈R(i)となります。
すなわちa,bは任意の実数ですからR(i)の元は全てa+biという顔をしていることがわかります。
(ここの所は多少厳密でないかもしれません)つまりR(i)=Cがわかりました。
このことから2次方程式が虚数解を持つ場合、R⊂R(i)=Cなる体の拡大を用意すればあらゆ
る2次方程式(係数も何でもよい)の全ての根(実根でも虚根でも)はR(i)=C
に含まれることがわかります。
実はCは代数的閉体と呼ばれ、数の中では最も広い体系をもち、2次といわず、
任意の次数の全ての方程式の根がCに含まれてしまうのです。
しかしながら今は方程式を代数的に、つまり4則演算と冪を何回も取ることで解
くことを話題としているので、Q⊂Q( )の拡大へ戻って進めていきましょう。
)の拡大へ戻って進めていきましょう。
さて、少し窮屈に感じるところは2次方程式の係数を有理数に制限しているところです。
この条件を取り去るにはどうしたらよいでしょうか?
任意係数の2次方程式を用意して、その係数を降冪の順にa,b,cとします。
(つまりaはxの2乗の係数、bはxの係数、cは定数項)
ここで、次の体を作ってみたらどうでしょう。
つまりQ(a,b,c, )
)
a,b,cは有理数とは限らないのでQ(a,b,c, )は
Q(
)は
Q( )の拡大体となり
2次方程式の根の公式と言うのはその係数と
)の拡大体となり
2次方程式の根の公式と言うのはその係数と で構成されているので、任意係数の2次方程
式の根は全てQ(a,b,c,
で構成されているので、任意係数の2次方程
式の根は全てQ(a,b,c, )に属していることになります。
)に属していることになります。
従って2次方程式の場合はQ( )⊂Q(a,b,c,
)⊂Q(a,b,c, )なる体の拡大を
作ってやれば全ての根が拡大しきった体Q(a,b,c,
)なる体の拡大を
作ってやれば全ての根が拡大しきった体Q(a,b,c, )の中に入る事がわかりました。
)の中に入る事がわかりました。
3次方程式や、4次方程式の場合もQにその係数と判別式にルートを取ったものを添加した体を
作ってやれば全ての根がその体の中に入ることがわかります。
そうすると、方程式が代数的に解ける
ということはQにその係数を全部添加した体(これをその方程式の定義体という)に
累乗根を次々と添加して体を拡大していくことによって全ての根を含む体を作ること
ができると言うことができます。
逆にいうと方程式が代数的に解けないとは全ての根
を含むような定義体の拡大体が作れないということです。

 E-mail
E-mail
 戻る
戻る
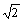 の紙で考えると,2回おる毎に長辺が半分になります。
の紙で考えると,2回おる毎に長辺が半分になります。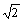 )の紙で10回折った状態と言うことになります。
)の紙で10回折った状態と言うことになります。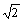 ですが,400mの設定もaboutなので)。
ですが,400mの設定もaboutなので)。
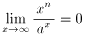


 が現れますがこれは有理数とは限りません。
が現れますがこれは有理数とは限りません。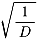 となり1/Dは方程式の係数を有理数に限定してあるのでやはり有理数です。
よって
となり1/Dは方程式の係数を有理数に限定してあるのでやはり有理数です。
よって E-mail
E-mail
 戻る
戻る