
Weekend Mathematics/コロキウム室/テーマ別/34.リングセオリー1
| NO.717 | 2000.1.7. | WAHEI | リングセオリー(1) |
(はじめに)
代数方程式の代数的解法シリーズ(テ−マ別の部屋)では体と群について、特に群は基本とはいえ、やや
深く理論を展開しました。これから気楽に群や体とは一味違った「環」について、紹
介したいと思います。
2000年になって、いろいろな問題が取り立たされているようですけど、さしあ
たって興味ある問題はやはり代数方程式の代数的解法についてなのですが、体と群に
よく似ている概念である環は実はその理論が現代語で展開されてからまだ100年も
たっておらず、そのためか極めて抽象的です。抽象的とは自由という言葉と表裏一体
なのですが、あまりに自由すぎて我々の常識をはみ出している感があり、自分が納得
するまでは多少の忍耐が必要かもしれません。(書道などの作品がなかなか理解され
ないのと似ているかもしれません)
しかし、とはいっても、やはり面白いものであると思います。まずは環の定義を書い
ておきましょう。
(定義)
集合Rが環であるとは、R≠φであって、写像mとnが次のように与えられているとす
る。
m:R×R → R
n:R×R → で対応は次の通り
m((a、b))=a+b
n((a、b))=ab
(このmをR上の足し算(あるいは和)、nをR上の掛け算(あるいは積)という)
そして、次の4つの性質を満たす。
(a+b)c=ac+bc
(ただし∀a、b、c∈Rで1≠0を仮定する)
R×RはRの元のペアーの集合でRとRの直積といいます。
そのRとRの直積からRへの写像
を実はR上の演算(正確には2項演算)というのです。
もちろん複素数上の(我々がよく知る)数の足し算や掛け算、引き算、割り算は全て
演算になっています。
上の定義は集合Rはそのように2つの演算、和と積が与えられていて足し算ではアー
ベル群
(代数方程式の代数的解法シリーズ参照)というのですから0が存在して∀a∈Rに対して−
aがあって、3つ以上の元は結合的に足す事ができてかつ可換と言う事です。
また2番目の条件は3つ以上の元はやはり結合的に掛けていいということでしょう。
3番目の条件は和と積が結びついたものです。これを分配法則とか分配律とか言います。
そして4は整数と類似の1があるという事です。
それから最後の括弧の中に奇妙なことが書いてあります。
環では0は単位元とは言わず、1を単位元といいますが、0は足
し算では単位元の役割を果たしています。
もし1=0ならば、どんな事が起こってくるのでしょうか?
∀a∈Rに対してもし1=0ならば両辺にaを掛けると、
a1=a0⇔a=0
となります。
aはRの任意の元でそれが0だというのですからR={0}となります。
ですから1≠0ならばR≠{0}ということです。もちろん逆もいえます。
またa0=0a=0は環の定義から証明できます。確かめてください。
注意してほしい事はいま集合Rというのは数に非常によく似ているけれども数よりも
広い概念であるという事です。
Rはφでなければ何でもいいのですから。
よってa0=0a=0も一応確かめておかねばなりませんね。(∀a∈R)
環の最も基本的な例は整数といえるでしょう。
代数方程式の代数的解法シリーズでも見たように、
整数は数の足し算でアーベル群でしたし、他の3つの公理も満たしますね。
よって整数は数の足し算と掛け算で環です。
また、環Rの定義を眺めてみるとab=baを仮定していない事に注意してください。
ところが群のところでも書いたように可換性がないとやはり不便です。
そこで環Rがab=baを満たすときその環を可換環(かかんかん)といいましょう。
(舌を噛みそうですけれどもね)
よって整数は可換環です。でも行列は可換環ではなく、純正な環です。(ただし行列
の足し算と掛け算で)
普通、可換性が成り立たない世界は極めて制御するのが難しくどんな場所へ行くのか
わからないミステリーゾーンのようなものですが、行列は割合扱いやすい最も優れた
非可換な環といっていいでしょう。以下ほとんど全ての環を可換環とします。
さて体の定義を思い出してください。
実は可換環の定義に掛け算に関する逆元の存在
を付け加えたものですよね。ですから体ならば自動的に可換環です。
また、体には準同型写像という大切な写像がありました。
あれは演算を保持し、単位元を単位元に移すものでした。
従って2つの環の間にも矛盾なく準同型写像を定める事ができます。
(環ならば和と積があり、かつ単位元1を持つので)
特に環の間の準同型写像を「環写像」という事にします。
(感謝状ではありませんよ)
体のときと全く同じようにも
し環写像が全単射ならその写像を環同型といい、それで結ばれる2つの環RとSは互い
に同型であるといい、R〜Sとかく事にしましょう。つまり、
R〜S⇔環同型f:R → Sが少なくとも1つ取れる。
です。
ここで群の時と同じように部分環を定義しておきましょう。
(定義)
Kが環Rの部分環であるとはK⊆Rであって、次の3つを満たすものとする。
さて、ここで環写像の例を2つほど挙げてみます。それぞれ確かめてみてください。
(例1)
f:C → C
を複素数から複素数への写像とする。
ただし対応はf(a+bi)=a−biとする。
また、これは環同型か?
(例2)
f:M(n) → M(n)
を成分を実数とするn次正方行列の集合から、その集合への写像とする。
ただし対応はf(A)=P‐AP
(P∈M(n)でその行列式が0でないとする。P‐はPの逆行列)
環写像(準同型写像)について忘れた方は
代数方程式の代数的解法シリーズの(3)を見てくださ
い。
さて、環写像を用いて環の内部にある部分集合を定めることができます。
(定義)
f:R → Sを環写像とする。Ker(f)とIm(f)を次で定義する。
Ker(f)={a∈R|f(a)=0}
Im(f)={f(a)∈S|a∈R}
さあ、この定義を吟味してみましょう。
Ker(f)というのは言葉でいうとfで移し
て0∈Sへ行くようなRの元の集合という事ですね。
Im(f)はRの元の像の集合という事でしょう。
このIm(f)をf(R)とも書きます。
どちらでも自分にあった方を
使ってください。人によってはf(R)の方がイメージが湧くかもしれません。
代数方程式の代数的解法シリーズの(2)
で写像の種類について定義しました。
単射、全射、全単射でし
たが、上のKer(f)とIm(f)を用いて、単射と全射の定義を改良しましょう。
すぐにわかる事ですが、fが全射⇔Im(f)=Sということです。
これは代数方程式の代数的解法シリーズの(2)で定義した全射の定義と同値です。
また、fが単射⇔Ker(f)={0}が成り立ちます。
これは少しわかりずらいかもしれませんが、定義(ルール)
に従って考えていけば簡単です。
(Ker(f)={0}⇔fが単射の証明)
まずKer(f)={0}を仮定する。この仮定のもとにfが単射である事を示す。
定義に従いf(a)=f(b)とする。
するとf(a)−f(b)=0であるから、f
は環写像なのでf(a−b)=0であり、Ker(f)の仮定からa−b∈Ker(f)である。
よっていまKer(f)={0}と仮定しているのだからa−b=0であり従ってa
=bを得る。ゆえにfは単射。
今度はfが単射である事を仮定してKer(f)={0}を示す。
∀aをKer(f)からとってこれが0である事をいえば題意は満たされる。
∀a∈Ker(f)を取ってくればKer(f)の定義からf(a)=0でである。いまfは
環写像なのだから、
f(0)=0 ・・・・・(1)
である。よってf(a)=f(0)で仮定よりfは単射であるからa=0.従って任意
のKer(f)の元は0ということなのでKer(f)={0}
さて、この証明の中にある(1)について考えてみましょう。fが環写像ならばほん
とに0が0へ移るのでしょうか?
環Rは和でアーベル群でした。
ですから、a+0=0+a=aが任意のRの元aについて成り立ちます。
この式をfでそれぞれ移して見ましょう。すると
f(a+0)=f(0+a)=f(a)
です。さらにfは和を和に移すので(なぜならばfは準同型写像なので)
f(a)+f(0)=f(0)+f(a)=f(a)・・・・(2)
となります。aはRの任意の元だったのでf(a)もSの任意の元としてもいいでしょ
う。(多少乱暴な言い方ですが)
してみると上の(2)の式をよく見てみるとf(0)はS内で0の役割をしていますよね。
任意のf(a)∈Sを和で変化させていないのですから。
つまりf(0)=0です。これで証明のなかの(1)がいえました。
それから、Ker(f)はカーネルエフと読んで、Im(f)はイメージエフと読みます。
これが一般的な呼び名とされているようです。しかし英語で書かれた本を読むと
いろいろと書いている人によって呼び名が(ほとんど統一されているとはいえ)微妙
に異なっている事があります。注意してください。
またIm(f)はSの部分環となっています。確かめてみてください。
ただしKer(f)はRの部分環にはなっていません。これもその理由を考えてみてください。
最後に問題を出しておきましょう。なかなかの良問です。
(問題)
R〜Sは環RとSが環同型で結ばれているという事でしたが、この〜はある集合上の同値
関係になっています。それがどんな集合かを決定し、〜が同値関係になっている事を
確かめてください。
解けても、解けなくても構いません。自分の頭を頼りにあれこれ創造してみてくださ
い。
次回は環構造を解析するうえで欠かす事のできない「イデアル」について考えてみま
しょう。

| NO.720 | 2000.1.12. | Junko | リングセオリー(2) |
NO.717で宿題になっていました、
「∀a∈Rに対して、a0=0a=0」の証明をしてみようと思います。
| a0 | =a(0+0) | ・・・0は加法の単位元であることから |
| =a0+a0 | ・・・分配法則より |

| NO.722 | 2000.1.14. | WAHEI | リングセオリー(3) |
まずは前回(NO.717)の補足をします。以下環と書いたら可換環とします。
集合Rを環としましょう。このとき次が成り立ちます。
f:R → Sを環写像とする。このとき
また、環の例を少し紹介したいと思います。
R=Z×Qを整数と有理数の直積とします。
このRに次で演算を入れて見ましょう。
まず和を次で定めます。
(a、x)+(b、y)=(a+b、x+y)
但しa、bは整数でx、yは有理数です。また右辺の括弧の中の+は数の+です。
そして積を次で定めましょう。
(a、x)(b、y)=(ab、ay+bx)
やはり右辺の積は数の積、和は数の和です。
まずこれが演算になっている事はいいでしょう。
a+bは整数同士の足し算ですから
やはり整数でx+yも有理数同士の掛け算なのでやはり有理数です。
ですから(a、x)+(b、y)∈Rです。
積のほうも明らかにR上の演算になっています。
またこれが環の定義を満たす事は腕力(計算力)です。
全てきちんとやっておきましょう。
(a、x)+((b、y)+(c、z))=((a、x)+(b、y))+(c、z)
はZもQも和でアーベル群だから自明。
(0、0)∈Rで∀(a、x)∈Rに対して
(a、x)+(0、0)=(0、0)+(a、x)=(a、x)はやはり自明。
よって(0、0)がRの0となっている。
(a、x)+(b、y)=(b、y)+(a、x)もZとQが和でアーベル群であること
からOK。
また∀(a、x)∈Rに対して(−a、−x)∈Rで両者足すと(0、0)となる。
以上よりRは上で定めた和によってアーベル群。
| ((a、x)(b、y))(c、z) | |
| = | (ab、ay+bx)(c、z) |
| = | ((ab)c、(ab)z+c(ay+bx)) |
| = | (abc、abz+cay+cbx)(a、x)((b、y)(c、z)) |
| = | (a、x)(bc、bz+cy) |
| = | (a(bc)、a(bz+cy)+(bc)x) |
| = | (abc、abz+acy+cbx) |
| (a、x)((b、y)+(c、z)) | |
| (a、x)(b+c、y+z) | |
| (a(b+c)、a(y+z)+(b+c)x) | |
| (ab+ac、ay+az+bx+cx)(a、x)(b、y)+(a、x)(c、z) | |
| (ab、ay+bx)+(ac、az+cx) | |
| (ab+ac、ay+az+bx+cx) |
この例のように環とは創ろうと思えば結構創る事ができる対象で、自分の手に触れる
事ができる貴重な数学的対象といえるでしょう。
上の例は基本的には数の和と積を用いています。
ですから、本質的には数の世界にある環といえます。
(もしかしたら上の例で計算ミスをしているかもしれません。
自分で確かめる際は注意してください)
ここで皆さんも自分で環を創ってみてください。
いろいろできるかと思います。
我々がよく知る環(整数や有理数、実数、行列など)の部分環を創ってみてもいいと思います。
部分環ならば環となりますし、(ただし母体としている環の和と積で)部分環
の定義は環の純粋な定義よりも簡単ですからね。
(従って、部分環を考える事は環論では非常に重要になってきます)
さて、ここでイデアルについて考えてみましょう。まずはイデアルの定義です。
(定義)
Ω(オメガと読みます)が環RのイデアルであるとはΩは空でないRの部分集合で次
の2つを満たす事を言う。
イデアルの定義はたったこれだけですが、今後、このイデアルは環を構成する上で決
定的な役割を果たします。
先ほど紹介した環などはまだまだ具体的で(それゆえ優れた環ですが)
抽象化はされていないといえます。
環を例えば対称群(NO.706 代数方程式シリーズ(4)を参照)のように自由に定義するには
一体どうすればいいでしょうか?
実はこのイデアルを用いて環をもっと自由に扱う事が可能となります。
余談ですが、イデアルというのは横文字で書けばidealですが、これは英語の発
音によるとアイデアルとか言います。しかし数学ではドイツ語風にイデアルと読みま
す。これを創った人がドイツ人だったのでしょうか?僕はどうもそんな気がします。
1994年に解決されたフェルマー予想の歴史でこのイデアルという概念が生まれた
のだそうです。フェルマー予想についてはいろいろな本が出版されていますので興味
のある方は読んでみるといいかと思います。
(このフェルマー予想の正しい証明は現在たった1つしか知られていません)
NO.717 リングセオリー(1)では環写像fを用いて環Rの中にKer(f)を定義しました
が、実はこれはRのイデアルになっています。確かめてみてください。
それから次の補題を証明しておきましょう。
(補題)
1∈Ω⇔Ω=R
但し、Rは環でΩはRのイデアルとする。
(証明)
1∈Ωを仮定する。Ωはイデアルなので∀α∈Rを取ってくると1α=α∈Ωである
から、R⊆Ωである。またイデアルの定義からΩ⊆RだったのでR=Ω
逆は1∈R=Ωから自明。
イデアルの定義だけからは1∈Ωはわからないわけですが、もしイデアルが1を含め
ば母体のRと一致してしまうというのです。これを用いると環Rの部分集合であるK
er(f)の大きさが大体わかります。
もし1∈Ker(f)ならば、定義よりf(1)=0ですが、fは環写像なのでf
(1)=1です。
よって1=0となり、環の定義(1≠0)に矛盾します。
だから、1はKer(f)に入っておらず、補題からKer(f)≠Rとなり、Ke
r(f)はRの真の部分集合という事がわかります。つまりKer(f)⊂Rです。
次回はこのイデアルをじっくりと味わって、さらに環論を展開していきましょう。

| NO.723 | 2000.1.15. | Junko | リングセオリー(4) |
NO.717 リングセオリー(1) の中の例1について考えてみます。
まずこの写像が準同型写像であることを示します。(例1)
f:C → C
を複素数から複素数への写像とする。
ただし対応はf(a+bi)=a−biとする。
また、これは環同型か?
| f(α)+f(β) | =f(a+bi)+f(c+di) |
| =(a-bi)+(c-di) | |
| =(a+c)-(b+d)i |
| f(α+β) | =f{(a+bi)+(c+di)} |
| =f{(a+c)+(b+d)i} | |
| =(a+c)-(b+d)i |
| f(α)f(β) | =f(a+bi)f(c+di) |
| =(a-bi)(c-di) | |
| =(ac-bd)-(ad+bc)i |
| f(αβ) | =f{(a+bi)(c+di)} |
| =f{(ac-bd)+(ad+bc)i} | |
| =(ac-bd)-(ad+bc)i |
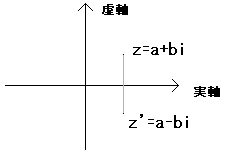
全単射であることは、
f(a+bi)=a−bi より、複素平面で上下をひっくり返すということで
、厳密にやらずに許してもらいましょう。
従って、これは環同型であるといえます。

| NO.724 | 2000.1.16. | Junko | リングセオリー(5) |
についてです。f(R)(Im(f)ともかきます。)はSの部分環となっていますが、Ker(f)はRの部分環にはなっていません。
f(R)についてです。
NO.717 リングセオリー(1)の中にある部分環の定義に従って示していきます。
Ker(f)はRの部分環にはなっていません。
なぜなら、fは準同型写像であるから、f(1)=1≠0です。
従って、1はKer(f)の元ではありません。
単位元を持ちませんから、部分環とはいえません。
(注)については、次のNO.725にて。

| NO.725 | 2000.1.16. | Junko | リングセオリー(6) |
についてです。f:R → Sを環写像とする。このとき
が正しい。
- f(−a)=−f(a)
- f(a−b)=f(a)−f(b)

| NO.726 | 2000.1.17. | Junko | リングセオリー(7) |
について確認してみます。環写像fを用いて環Rの中にKer(f)を定義しました が、実はこれはRのイデアルになっています。

| NO.731 | 2000.2.1. | WAHEI | リングセオリー(8) |
NO.726 リングセオリー(7)でJunko先生は環写像のカーネルが環Rのイデアルであること
を調べてくれました。それについての僕の考えです。
解く方法は全く申し分ありませんが、イデアルの定義に従って、一応カーネルエフが
空集合でない事を確認しておきましょう。
まず、f:R → Sを環写像としましょう。
Ker(f)={a∈R|f(a)=0}でした。
環写像の性質からf(0)=0です。
ですから、0∈Ker(f)となって、Ker(f)は空ではないことがわかります。
また、イデアルの定義の2番目をよく見てください。
スカラーは広いRから取らねばなりません。
Junko先生は惜しい事にKer(f)の中だけで考えてしまいました。
∀α∈R、∀a∈Ker(f)を取ってきます。そしてαaをfで移してみます。
f(αa)=f(α)f(a)
となり、a∈Ker(f)ですからf(a)=0従って上の式は
f(αa)=f(α)f(a)=f(α)0=0 (0には何を掛けても0なので)
よってf(αa)=0となり、αa∈Ker(f)です。
和のほうはJunko先生のやり方で申し分ありません。ですからKer(f)はRのイデアルで
ある事がわかります。

| NO.732 | 2000.2.2. | WAHEI | リングセオリー(9) |
今回の目標はイデアルを味わった後に群論からの追加項目を踏まえてファクターリン
グの概念を得る事にあります。
まずイデアルの復習ですが、イデアルとは可換環Rの空でない部分集合で和について
閉じていてかつ、環Rから取った勝手な元についての積について閉じているという事
でした。
イデアルの定義は非常に簡単ですが、この定義の成す単純さと、それから出
てくるイデアルの多様性は不思議な対象性を成しています。
イデアルの定義から次の事がすぐにわかります。
(イデアルの基本性質)
Ωを可換環Rのイデアルであるとすれば、次が正しい。
ここでイデアルの例を考えてみましょう。
整数全体をZで表します。
Zは数の足し算と掛け算で環でした。
ここで環であることを強調するためにZのことを「整数環」と呼ぶ事にしましょう。
我々が知っている環はそう多くありません。
ですからこの整数環は今のところ我々にとって命綱のようなものですから
大切にしなくてはなりません。
今後抽象的な環がいくつか登場してきますが、我々は抽象化されすぎてよくわか
らなくなったときには常にこの整数環に立ち戻って考える事にしましょう。
さて、(n)={nχ|n∈Z、χ∈Z n≧2}と定義します。
もちろんnχは数の掛け算ですが、この(n)は良くわかるようにn
の倍数の集合ですね。
また、nは2以上の整数ですから1は(n)には入っていません。
従って、NO.722 リングセオリー(3)の補題によると、これは全体(すなわちZ)と一
致しないという事もわかります。
かつ、この(n)はZのイデアルになっています。
なぜならば、もちろん(n)≠φであって、∀a、b∈(n)を取ると(n)の定義
からa=nχ、b=nyという顔をしていて
a+b=nχ+ny=n(χ+y)
となり、χもyも整数ですから括弧の中も整数です。
ですからa+bもnの倍数となり、(n)の元です。
一方、∀α∈Zに対して、αa=α(nχ)=(nχ)α=n(χα)∈(n)
(χα∈Zなので)
よって(n)はZのイデアルです。
ですから上に書いたイデアルの基本性質は全て満たします。
ここでイデアルの基本性質の(3)を見てください。
何か思い出す事はないでしょうか?
環Rと言うのは和でアーベル群でした。代数方程式シリーズでも説明しましたが
群には部分群という大事な概念がありました。
ΩをRのイデアルとするとΩは空でなくて、かつ∀a、b∈Ωに対して、
基本性質の(3)から、a−b∈Ωです。
これはイデアルΩが環Rの部分群である事を言っています。
ただし演算は和です。
(NO.706 代数方程式の代数的解法(4)では演算は積で表していましたが、
それを和に変えただけです)
部分群を用いる事で母体の群に2つの同値関係を定める事ができました。再掲してお
きますと、
R1={(a、b)|−a+b∈Ω}
R2={(a、b)|a−b∈Ω}
です。但し今は可換環Rを群と見なしています。注意してください。(定義から環は
和でアーベル「群」なのですから、そう見なしても何ら矛盾は生じません)
このR1とR2をよくよく眺めてみるとR1=R2となっている事に気が付くと思い
ます。
さあ、代数方程式シリーズでは不本意ながら書くことができなかった正規部分群につ
いて書くときが来ました。
(定義)
群Gに対してその部分群Hが正規部分群(normal sub group)であるとは
∀a∈Gに対してaH=Haが成り立つ事を言う。
復習ですがaH={ah|h∈H}でした。
Haについても同様です。
上の定義はaHとHaが集合として等しいとき、HをGの正規部分群であると呼ぼうというこです。
もう少し丁寧に観てみますと、任意のGの元と可換な部分群を正規部分群と言うのです。
この事からすべてアーベル群の部分群は正規部分群となっている事がわかります。
するとどうでしょう?可換環Rは和でアーベル群でした。ですからその部分群である
イデアルは和で正規部分群を成している事がわかります。
またイデアルに関してはR1=R2でした。
(イデアルと環の定義からすぐ出てきますので確かめてください。
でも頭の中でできてしまうかもしれません)実はこの事実は一般化できます。
(命題)
Hを群Gの正規部分群とするならばR1=R2が成り立つ事が必要にして十分であ
る。
(証明)
群論のレベルに戻って証明します。従って演算は積とします。
まずHを群Gの正規部分群とします。
aR1bとするとa‐b∈H。
よってHの元hを用いてa‐b=hと書け、従ってb=ah∈aH=Ha(仮定から)ですので
b=ka(k∈H)と書けます。
ですからba‐=k∈HとなってbR2a。
R2は同値関係ですのでaR2bとなって、R1⊆R2
全く同様にしてR2⊆R1も示せますから、暇なときにでも確かめておいてくださ
い。よってR1=R2です。
今度は逆を示します。
つまり、R1=R2を仮定してHが正規部分群である事を示します。
示すべきはaH⊆Haかつ、Ha⊆aHです。
(確認しておきますが、2つの集合が等しいと言う事はこういうことでした。)
∀χ∈aHを取るとχ=ah(h∈H)と書けます。
これはaR1χを意味しますから仮定によってaR2χとなり、従ってaχ‐∈Hです。
HはGの演算で群ですから(aχ‐)‐=(χ‐)‐a‐=χa‐∈Hです。
(群だから、当然逆元も入っている)
これはχ∈Haを意味します。ですからaH⊆Ha。
さて、次は∀y∈Haを取ってくるとy=ka(k∈H)と書けて、よってyR2aより仮
定からyR1aで従ってy‐a∈H。
Hは群なので(y‐a)‐∈H⇔a‐y∈Hで
これはy∈aHを表しています。ですからHa⊆aH
∴aH=Ha (証明終わり)
この事から可換環R上にそのイデアルΩが定める同値関係R1とR2は等しいということ
がわかりました。つまり、RのR1による商集合とR2による商集合は一致します。商集
合と言うのは同値関係によって1つの集合がバラバラに分割されるわけですが、その
破片(ピース)の集合でした。
(詳しくはNO.709 代数方程式の代数的解法(7)を見てくだ
さい)
ここでR/R1=R/R2ですがこれをR/Ωと書くことにします。これを可換環Rのイデア
ルΩによるファクターリング(factor ring)といい、日本語では商環と言います。
ではR/Ωの演算はどのように定めたらいいでしょうか?
また、それ以前にR/Ωの元はどのような形をしているのでしょうか?
今まで準備した事を使えば簡単にわかりま
すが、それにしてもR/Ωの内部構造については次回に詳しく考えて見ましょう。

 戻る
戻る
 次へ
次へ