
Weekend Mathematics/コロキウム室/2000.1〜3/NO.87
| NO.751 | 2000.2.21. | WAHEI | リングセオリー(19) |
Galois Theoryの扉を開く前に、
これまでの事を整理してもらうために問題をいくつか用意しました。
そのいくつかは代数方程式シリーズ、
これまでのリングセオリーシリーズから
そのまま抜粋したものです。
(問題1)
体の定義を自分の言葉で書いてください。
(問題2)
代数方程式が代数的に解けるとはどういうことですか?
(問題3)
群の定義を自分の言葉で書いてください。
(問題4)
部分群とは何ですか?
(問題5)
2つの合同な正三角形Sの各頂点に1,2,3と番号を付けます。
この2つの正三角形Sを重ね合わせる操作をSからSへの写像と見なして、
その操作の集合は写像の合成を演算として群をなすことを確かめて下さい。
(問題6)
問題5で得られた群と3次対称群を比較してください。
(問題7)
次の命題について、自分なりに考えた事をレポートにまとめてください。
「群とは図形の対称性を記述するものである」
(問題8)
環の定義を自分の言葉で書いてください。
(問題9)
f:R→Sが環同型であれば、その逆写像f‐:S→Rも環同型であることを確かめて下さい。
(これは少し高級です)
(問題10)
Qを有理数の全体とします。このとき写像f:Q→Qが環写像ならばfはQ上の恒等写像である事を示してください。
(これも少し高級。)
(問題11)
Rを可換環としAとBをRの2つのイデアルとしますと、
その共通部分A∩BもRのイデアルであることを確かめて下さい。
(問題12)
Rを可換環としXをその空でない部分集合とします。
このときA:={a∈R|∀x∈Xに対しxa=0}はRのイデアルであることを確かめて下さい。
(問題13)
kを体とします。このときk[X]はPIDである事を証明してください。
(問題14)
代入原理について思った事をレポートに書いてみてください。
(問題15)
Rを可換環とします。
a∈Rがベキ零元(nilpotent element)であるとはある正の数nについて
an=0となるものを言いますが、これはZDである事をうまくnを取る事で証明してください。
(問題16)
Rを可換環とします。SがRの積閉集合であるとはSは空でないRの部分集合で
∀s、s’∈S⇒ss’∈Sでかつ1∈Sを満たす事を言います。
このときRとSの直積集合R×Sに関係〜を次で定めます。
(a、s)〜(a’、s’)⇔t(sa’−s’a)=0 (tはあるSの元)
この〜はR×S上の同値関係である事を確かめて下さい。
(計算力が必要です)
(問題17)
Zを整数環とします。
pを素数とするとき、ファクターリングZ/(p)は体である事を示してください。
(問題18)
RとSを可換環とし、f:R→Sを環写像とします。
このときΩがSの素イデアルならばそのfによる原像f‐(Ω)はRの素イデアルであること
を示してください。
ざっと18問ありますが、僕は与えられた問題を正確に早くこなす能力だけが
数学の能力であるとは思っていませんから、
自分のペースでやってくださって全く結構です。
また別に問題1から順を追って進まなくてもいいようにしてあります。
自分が興味を持った問題からやってもいいし、最初からやってももちろん構いません

| NO.752 | 2000.2.21. | Junko | 無限級数の和(3) |
前の結果を使いながら、NO.750 無限級数の和(2)でやったのと同じ要領でやっていけば、
順に次数を上げていくことができそうです。
まずは3次式

次は4次式

この調子でいくと、n次式について一般形も導けそうですね。

| NO.753 | 2000.2.22. | 水の流れ | 無限級数の和(4) |
「Mathematica」で分子の次数を上げていきました。
14次まで上げましたが、10次までの分を載せます。
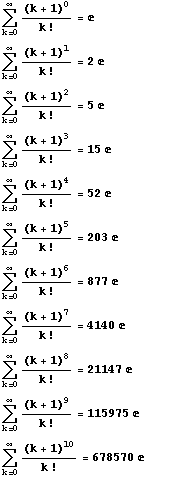

| NO.754 | 2000.2.22. | 水の流れ | 無限級数の和(5) |


| NO.755 | 2000.2.24. | 水の流れ | 無限級数の和(6) |
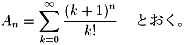
(ただし、n=0,1,2,3,・・・で、A0=eなる)
f0(x)=exとおくと、f’0(x)=ex で
f’0(1)=e
f1(x)=x f’0(x)=xexとおくと、
f’1(x)=(1+x)ex で f’1(1)=2e
f2(x)=x f’1(x)=(x+x2)exとおくと、
f’2(x)=(1+3x+x2)ex で f’2(1)=5e
f3(x)=x f’2(x)=(x+3x2+x3)exとおくと、
f’3(x)=(1+7x+6x2+x3)ex で f’3(1)=15e
f4(x)=x f’3(x)=(x+7x2+6x3+x4)exとおくと、
f’4(x)=(1+15x+25x2+10x3+x4)ex で f’4(1)=52e
・・・・・ これを同じように繰り返していきますと、
fn+1(x)=x f’n(x)となり、
求める極限値は An+1=f’n+1(1) として表される。
さらに、f’n(x)の係数を表にします。
| J/M | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 計 |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | ||||||
| 1 | 1 | 1 | 2 | |||||
| 2 | 1 | 3 | 1 | 5 | ||||
| 3 | 1 | 7 | 6 | 1 | 15 | |||
| 4 | 1 | 15 | 25 | 10 | 1 | 52 | ||
| 5 | 1 | 31 | 90 | 65 | 15 | 1 | 203 | |
| 6 | 1 | 63 | 301 | 350 | 140 | 21 | 1 | 877 |

| NO.756 | 2000.2.24. | 水の流れ | 無限級数の和(7) |
n個の異なる要素を持つ集合を空でないk個の部分集合に分ける方法は何通りありますか

| NO.757 | 2000.2.25. | Junko | 無限級数の和(8) |
NO.752 無限級数の和(3)の続きです。
A0=e、A1=2e、A2=5e、
A3=15e、A4=52eをふまえて、
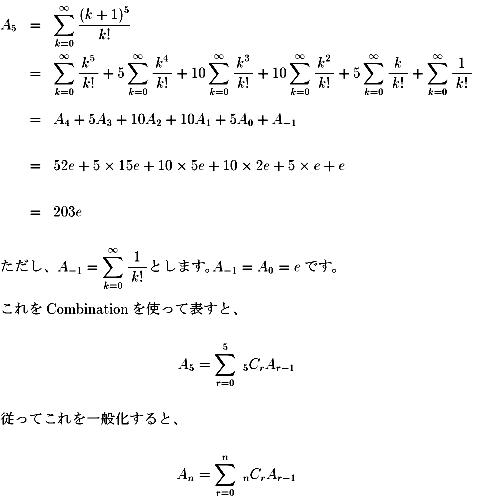
これに沿って、A6を求めてみます。
| A6 | =A5+6A4+15A3 +20A2+15A1+6A0+A−1 |
| =203+6×52+15×15+20×5+15×2+6+1 | |
| =877 |
調子にのって、もう1つ
| A7 | =A6+7A5+21A4+35A3 +35A2+21A1+7A0+A−1 |
| =877+7×203+21×52+35×15+35×5+21×2+7+1 | |
| =4140 |
二項展開のような感じで計算できます。
これは、NO.753 無限級数の和(4)で
「水の流れ」さんが計算してくださった結果と一致しています。

| NO.758 | 2000.2.25. | 月の光 | 「三角の問題」の発展 |
今月の問題35「三角の問題」の発展問題です。

「三角の問題」の図で∠r=θ1 、∠q=θ2 、
∠p=θ3とします。
次にその三つの正方形の左側にn−3個の正方形を同じように繋げます。
すると全部でn個の正方形が繋がった形になるので、右からm番目の
正方形にある角度をθmとします。
説明が不適当かと思いますが、
つまり tanθm=1/mということです。

この問題には今までコロキウム室で使ってきた関数や定数を使った
とても不思議で面白い結果が待っています。
そのためにゼータ関数、ガンマ関数、オイラー数γ(=0,577…)の復習と、
複素平面におけるarg(偏角)の理解をしておいて下さい。

| NO.759 | 2000.2.25. | Junko | 階段の問題 |
第10回・数学オリンピック予選において次のような問題が出題されています。
一歩で1段、2段、または3段を登れる人が、7段の石段を登る。 何通りの登り方があるか。 ただし途中で下りたり、足踏みしたりはしないものとする。

| NO.760 | 2000.2.25. | WAHEI | リングセオリー(20) |
今後の理論のために必要な事を多少準備します。
(準同型定理)
f:R→Sを環写像とします。ΩをRのイデアルとし、Ker(f)⊇Ωを仮定します。
また、ε:R→R/Ωをε(a)=a+Ωで定めますと、これは環写像で、かつ全射でした。
(NO.749 リングセオリー(18)参照)
このとき、環写像g:R/Ω→Sがgε=fを満たすように一意的に決まります。
(証明)
まず、上のように定めた写像gがwell-definedなことは、
a+Ω=b+Ω
を仮定すれば、a−b∈Ωですから、Ω⊆Ker(f)を考えれば、a−b∈Ker(f)で、
よってf(a−b)=0。
fが環写像である事を考えれば、f(a)−f(b)=0ですので、
f(a)=f(b)。
これはgがwell-definedである事を示します。
また、このgが一意的に決まる事は、gと同じ性質を満たすg’が存在したとして
g=g’を示せばいいのです。しかし、これはfが与えられている以上、自明です。
最後に、gが環写像である事を観ておきましょう。
g((a+Ω)+(b+Ω))=g((a+b)+Ω)
=f(a+b)=f(a)+f(b)=g(a+Ω)+g(b+Ω)より、和はOK。
g((a+Ω)(b+Ω))=g((ab)+Ω)=f(ab)
=f(a)f(b)=g(a+Ω)g(b+Ω)より、積もOK.
ですから、1も1へ移ります。よって、gは環写像です。 (証明終わり)
この結果を準同型定理といいます。この定理から、直ちに次の、極めて有意義な結果を得ます。
(第一同型定理)
上と同じ仮定の元に、f:R→Sが全射ならば、R/Ω〜Sが正しい。
(証明)
準同型定理から、環写像g:R/Ω→Sがgε=fを満たすように一意的に取れます。
このgが全単射である事を示せばいいことになります。
まず、これが全射であることは、fが全射である事に従います。
(これについては下の補題を見てください)
また、単射である事は、Ker(g)={0}を示せばよいので、∀a+Ω∈Ker(g)を取りますと、
カーネルの定義からg(a+Ω)=0.
ところで、g(a+Ω)=f(a)なので、0=f(a)で、
環写像の性質からa=0。よって、Ker(g)={0}がわかります。 (証明終わり)
この他にも第2、第3同型定理がありますが、
それらはこの第一同型定理から芋ずる式にでてきますので、
ここでは特にやりませんけども、機会があれば、そのつど紹介しましょう。
(補題)
f:A→Bとg:B→Cをそれぞれ写像とします。
すると、Bが共通ですのでその合成gfが作れます。このとき、次が成り立ちます。
gfが全射ならば、gが全射。
(証明)
gfが全射なので、Cの任意の元に対して、Aの元が対応します。
Aの元はfによってBへ移されていますから、結局gが全射という事になります。
(証明終わり)
また、次も成り立ちます。
(補題2)
上と同じfとgについて、その合成gfが単射ならば、fが単射。
これについては簡単ですので確かめてみてください

 E-mail
E-mail
 戻る
戻る