
Weekend Mathematics/コロキウム室/2000.1〜3/NO.80
| NO.700 | 2000.1.1. | Junko | 謹賀新年 |
2000年、あけましておめでとうございます。
今年はどんな年になるのでしょうか?
皆さんに支えられて、これからも一生懸命がんばろうと思います。
どうぞよろしくお願いいたします。

| NO.701 | 2000.1.1. | Junko | ミレニアム(3) |
問題2
(1)2000=24・53と素因数分解できるので、
5・4=20(個)
一般に、N=ap・bq・cr・・・と素因数分解されるとき、
約数の個数は、(p+1)・(q+1)・(r+1)・・・となります。
(2)次の式を展開すると、5・4=20の項が現れて、それが2000のすべての約数となります。
| (1+2+22+23+24)・(1+5+51+52+53) | |
| = | 31・156 |
| = | 4836 |
(3)約数の逆数の和に2000をかけると、逆数の和になります。
| 2000・(1/1+1/2+1/4+・・・+1/2000) | |
| = | 2000+1000+500+・・・+1 |
| = | 4836 |
| 1/1+1/2+1/4+・・・+1/2000 | |
| = | 4836/2000 |
| = | 1209/500 |
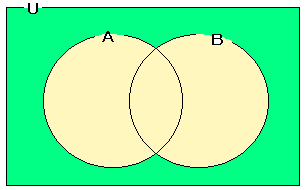 (4)
次の集合を定義します。
(4)
次の集合を定義します。
U={n|nは1〜2000の自然数}
A={n|nは2の倍数、n∈U}
B={n|nは5の倍数、n∈U}
A∩B={n|nは10の倍数、n∈U}
それぞれの集合の要素の個数をnで表すと、
n(U)=2000
n(A)=1000
n(B)=400
n(A∩B)=200
A∪Bの補集合(右図の黄緑の部分)の要素の個数を求めればいいので、
2000−{1000+400−200}=800
(5)それぞれの集合の要素の総和をSで表すと、
| S(U) | =1+2+3+・・・+2000 |
| =2,001,000 |
| S(A) | =2+4+6++・・・+2000 |
| =1,001,000 |
| S(B) | =5+10+15++・・・+2000 |
| =401,000 |
| S(A∩B) | =10+20+30+・・・+2000 |
| =201,000 |
(6)
1組見つけたところで、先が見えてきた・・・。
連続する自然数が奇数のとき、それをpとすると、
pN=2000 という式になります。
これを満たす奇数p=1,5,25,125の4つのみとなります。
連続する自然数が偶数のとき、それを2mとします。
2mN+m=m(2N+1)=2000という式になります。
(2N+1)は奇数ですから、これを満たすのは、2N+1=1,5,25,125の4つのみとなります。
以上により、答えは3つ。
398+399+400+401+402=2000
68+69+70+・・・+92=2000
47+48+49+・・・+78=2000
(7)123=1728 なので、2000−1728=272
これから立法数を引いたり足したりして0になればいいわけです。
123+63+43+(−2)3
=1728+216+64−8=2000
123+73+(−4)3+(−2)3+1
=1728+343−64−8+1=2000
まだまだたくさんありそうな雰囲気ですよ・・・。
そうそう8個という条件がありましたね・・・、でも個数は少なければその方がいいと言う気がしますがいかがでしょう?

| NO.702 | 2000.1.1. | WAHEI | 代数方程式の代数的解法(2) |
part 2
前回のNO.699 part1では気の赴くままに書いてしまい、
投稿の計画やどこまで語るかの方向性を書くのを忘れてしまいました。
part2ではこれから先進んでいくための多少の道具を用意しつつ
僕がなぜこれを書こうと思ったかの動機を(忘れなければ)書いていこうと思います。
まずは写像と言う概念です。高校では参考書には載っているのをたまに見かけます
が、写像は数学を組み立てていく上で決定的な役割を果たします。ここでその定義を
書いておきましょう。
(定義)
AとBをどちらもφでない集合とする。
A×B={(a,b)|a∈A、b∈B}としてこれをAとBの直積という。
さて、g:A → B が「AからBへの写像である」とは次の3つを満たすことをいう。
注意すべきは3番目の条件でしょうか。
これを写像のwell-defined性といいます。
つまり出発点(aのこと)が固定されていれば行き着いた先(bのこと)も同じになっ
ていないといけないということです。
この定義は数学的過ぎてかえって混乱するかも
しれませんが、噛み砕いて言うと
「写像gとはAの各元についてBの元を対応させる規則である」ということです。
つぎは写像の種類について定義しておきましょう。
(定義)
g:A → Bが単射であるとは∀a,b∈Aについてg(a)=g(b)⇒a=bということ
g:A → Bが全射であるとは∀b∈Bについてb=g(a)となるaがA内に存在すること
g:A → Bが全単射であるとはgが全射かつ単射であるということ
gが単射ならば定義からg(a)≠g(b) ならばa≠bということですからつまりAの元とB
の元が1つ1つ対応しているということがわかります。
またgが全射ならばBの全ての元はAからやってくる、
つまりBの元は根元(a∈Aのこと)を持つというように解釈できます。
最後にgが全単射の場合を考察しておきましょう。
定義からgは1つ1つ、かつ残りなく対応しているということですので、
実はgが全単射ならばAの元の個数とBの元の個数が等しいということが言えます。
NO.699 part1ではアーベルが体を用いて代数方程式の構造を調べたと言うことを書きました。
なぜこんな写像と言うものを定義したのかピンとこないかもしれません。
しかしある種の写像が全単射であればその写像によって結ばれた2つの集合が数学的に
(見掛けは違っていても)全く同等の構造をもつと見なせるのです。
NO.699 part1で5次以上の方程式には根の公式がないことを証明したのは2人いると述べました。
一人はアーベルですが、もう1人はガロアという人です。
ガロアはアーベルが見つけた体をそれよりももっと単純な構造をもつ
「群」という集合に置き換えて方程式の謎を解明しました。
そのときガロアが考え出したアイデアが体と群との間に全単射な写像を定めることだったのです。
しかしながら、そのアイデアはあまりにも時代を先行しすぎていて
当時(1830年ごろ)の人々には全く理解されませんでした。
part3ではこの群の定義をして5次以上の代数方程式には根の公式が存在しないとい
うアーベルの定理を紹介したいと思います。
そうそう、僕が投稿しようと思ったきっかけはコロキウム室が大変面白かったこと
と、そのコロキウム室に寄せられている話題がどちらかといえば解析系であるなと
思ったからです。またアーベルの定理について何気なく触れられているものの、やは
り方程式を解析的に近似を用いて解いているのを見かけました。
方程式を代数的に解くということがどれだけ深い数学を必要とするか、
他の読者の人々にも漠然とでもいいので理解されれば、
僕の意図は相当程度達成されたことになります。

| NO.703 | 2000.1.1. | 水の流れ | 2000 |
「12の数をいくつか使って、2000になる数式を作ってください。」
勿論、四則演算、( )、平方根、階乗、ガウス記号の使用は可能です。
一番シンプルな綺麗なものから、とにかく できたという感動を味わってください。
元旦にあたって、【「Weekend Mathematics 】のさらなるご発展を祈念します。

| NO.704 | 2000.1.1. | WAHEI | 代数方程式の代数的解法(3) |
part 3
NO.699 part1ではアーベルのアイデア (方程式が代数的に解けるとは全ての根を含むような 定義体の拡大の列が作れる)をざっと紹介しました。 part3ではまず群を定義して、ガロアのアイデアを述べてみたいと思います。 その後に数学(もちろん高校数学も含 みますが)を根底から支えている、ある3つの公理を紹介したいと思います。
さてと、群ですが、これはもともとコーシーという数学屋さんが作った(らしいので
すが)ものですがコーシーが考えていたのは無限集合であって、有限集合で群を打ち
立てたのは本質的にガロアです。
驚くことですがガロアはこのアイデアを牢獄の中で思いついたらしいのです。
(定義)
集合Gが群であるとは、G≠φであって、Gには1つの演算(掛け算と同じ表し方をし
ましょう)が与えられていて次の3つを満たすものをいう。
この定義も体のときと同様、何やら普通の数と似ています。
しかし1つだけ腑に落ちないところは可換性を仮定していません。
つまりab=baが成り立たなくても上の定義さえ満たしていればその集合を群というのです。
なぜ、可換性を一般に仮定しないのでしょうか?
いろいろ叫ばれているところですが、歴史的に見ると群とは2つの合同
な正多角形を重ね合わせる際に現れる現象を数学的に記述したもので、そのためか数
の一般化という意識が低く、可換性を仮定し忘れたとも言われています。
考えてみれば図形の張り合わせ方をベースにして上のような一般的な定義にするというのは大変
な努力が費やされたに違いありません。
その意味では現代に生まれている我々は先人の努力に対して謙虚にならなければならないでしょう。
脱線してしまいましたが、それにしても実際問題として可換性がないと不便でどうし
ようもありません。そこで、群がab=baを満たすということも仮定しておきましょ
う。(特にそのような群をアーベル群といいます)
さてアーベル群の例を調べておきましょう。演算を普通の数の足し算としてみると整
数全体(Zで書きます)はアーベル群です。なぜならば、まずZから勝手に2つの元を
取ってきます。(元とかいうふうに物々しく書いていますが要するに2つの整数を
取ってくると言うことです)それをa,bで書きましょう。するとa+bはもちろん整数
で従ってZの元です。よってZには数の足し算が演算として与えられていることがわか
ります。またa+(b+c)=(a+b)+cは整数の世界では常に成り立っていますので定義の1
もOKです。さて0は整数です。(0は自然数ではありません)そしてよく知られてい
るように∀a∈Zに対してa+0=0+a=aが成り立ちます。よって定義の2もOKでZでは数の
足し算においては0が単位元ということですね。そして3番目ですが、a∈Z⇒-a∈Z
ですので両者をたすと0となり以上のことからZは数の足し算でアーベル群です。
ところがZは数の掛け算では群になりません。惜しいことに定義の3を満たさないの
です。掛け算の場合(それがZの演算になっていることは明らかでしょう)単位元は
数の1です。しかしax=1となるxは整数に入っているとは限りませんからね。
(例としてはa=2とするとx=1/2となり1/2は整数ではありません)
でもZは数の足し算でアーベル群ですので、Q(有理数)もR(実数)もC(複素数)も
足し算でアーベル群であるということが予想されます。これは実に自然な予想で正し
い予想です。まとめてみると・・・
(定義)
AとBを共に体とする。g:A → Bが準同型写像であるとは、gは写像で次の3つを
満たすことをいう。
(数学を根底から支える重要な3つの公理について) その名前は

| NO.705 | 2000.1.2. | 水の流れ | 4444で2000 |
皆さん! 4を4回使って、いろいろな自然数をつくるゲームをご存知でしょう。
以前、このコロキウム室にもありましたね。
(テ−マ別の部屋、4444の問題)
では、2000年にあたって、この2000作るに挑戦します。
その前に、記号を理解ください。
.4=0.4 , ..4=0.04 , ...4=0.004 ・・・ を意味します。
また、
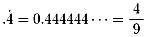
(循環小数)を意味します。では、作ってみます。
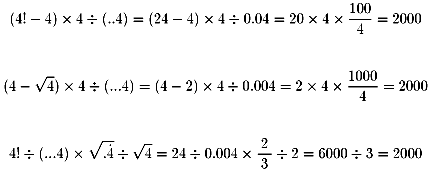

| NO.706 | 2000.1.2. | WAHEI | 代数方程式の代数的解法(4) |
part 4
まずは写像の合成を説明しておきましょう。
f をAからBへの写像、g をBからCへの写像としましょう。
∀a∈Aをf でBへ移します。
するとf(a)∈Bですが、今度はこのf(a)をgでCへ移します。
つまりg(f(a))∈Cとなります。
このg(f(a))を(gf)(a)と書くこと
にして、(gf)を写像f とg の合成といいます。
(gf)は明らかにAからCへの写像となります。
2つの写像において集合Bが共通していることに注目してください。
電車でいえばこのBが連結器の役割をしているといえましょう。
帰納的に(ドミノのように)何個かの集合がありそれぞれの間に少なくとも
1つの写像が定められていればそれぞれを合成して最初の集合と最後の集合の間に
1つの新しい写像を定めることが出来ます。
ここで、ある重要な群の例を紹介しておきましょう。
(対称群)
Xをφでない集合としましょう。
そしてXとXの間に写像を定めてやればそれが全単射
になるようにできるはずです。
というのもXからX、つまり自分自身への写像ですか
ら、当然元の個数だって等しいはずなのでうまく対応をつけてやれば全単射にするこ
とが出来るでしょう。
このとき(写像が全単射のとき)逆写像を定めることが出来ます。
fをXからXへの全単射としましょう。
∀a∈Xを取ってb=f(a)とおきます。
fの逆写像とはこのbに対してaを対応させるものです。
つまりfの逆写像をf‐でかけば、
上のb=f(a)をf‐でXへ移すと
f‐(b)=f‐(f(a))=a
となるということです。
ここで次の集合を考えましょう。
S(X)={f|fはXからXへの全単射}
この集合は数の集合ではありません。
そのへんが多少抽象的でわかりにくいと思いますが、S(X)は写像の集合です。
簡単のため、X={1,2,3}として考えてみましょう。
いま写像fは{1,2,3}から{1,2,3}への全単射な写像です。
このときS(X)を具体的に書き出すことを考えてみましょう。
まず1を1へ、2を2へ、3を3へ移す写像がありますよね。
つまりXのすべての元を固定する写像です。
(この写像を恒等写像といいます)
これを(1 → 1、2 → 2、3 → 3)と表すことにしましょう。
次に考えられるのは1を固定して2を3へ、3を2へ移す写像があります。
これを同じように(1 → 1、2 → 3、3 → 2)と書きましょう。
さて次はどうすればいいのかな。前の2つの写像では1の行き着いた先が1でした。
(つまり1が固定)そこで今度は1の行き着いた先を2にして考えてみましょう。
すると(1 → 2、2 → 3、3 → 1)と
(1 → 2、2 → 1、3 → 3)の2つが考えられます。
ではつぎは1の行き着いた先を3にして考えてみればよさそうです。
このときは(1 → 3、2 → 1、3 → 2)と(1 → 3、2 → 2、3 → 1)となります。
これで全部でしょうかね・・・・・うん、全部です。
よってS(X)は今書き出した6つの元で構成されています。
さて、S(X)から2つの元f、gを取ってきましょう。
S(X)の定義からこの2の写像は
全単射ですが、その合成(gf)を考えてみましょう。
fもgも全単射なのでその合成も全単射なのではと予想できますが、実際に証明してみましょう。
示すべきは(gf)が単射かつ全射ということです。
∀a、b∈Xについて
(gf)(a)=(gf)(b)とすると合成の定義からg(f(a))=g(f(b))となりg は全単射なので単
射、従ってf(a)=f(b)よってfはやはり単射だからa=bとなり(gf) は単射。
また、∀c∈Xに対してgが全射なのでg(d)=cとなるdが存在し、さらにfが全射なのでdに対
しd=f(e)なるeが存在している。
よって(gf)は全射でもある。
以上のことからf,gが全単射なら(gf)も全単射であることがわかりました。つまり(gf)∈S(X)です。
また恒等写像はS(X)内に必ず存在していますので、S(X)≠φです。
ところで、AからBへの2つの写像f,gが与えられたとき写像が等しいということ、
つまりf=gを∀a∈Aに対してg(a)=f(a)で定義しましょう。すると
(f(gh))(a)=f(gh(a))=f(g(h(a)))
((fg)h)(a)=(fg)(h(a))=f(g(h(a))) (∀f,g,h∈S(X), ∀a∈X)
ですから、f(gh)=(fg)hがS(X)内で成立しています。
また恒等写像を1で書くことに
すると(これは数の1とは違います。写像です)
∀a∈Xについて
1(a)=aですから(恒等写像は全ての元を固定するので)
(f1)(a)=f(1(a))=f(a)
(1f)(a)=1(f(a))=f(a)
となり、1f=f1=fが成り立ちます。
また∀f∈S(X)は全単射なので逆写像があり、
その定義から(ff‐)(a)=1(a)、(f‐f)(a)=1(a)ですので、
ff‐=f‐f=1が成り立ちます。
ここまでで不思議なことがわかりました。
すなわちS(X)は写像の合成を演算にして群になるのです。
NO.704 part3では群は数や行列と似ていると書きましたが、ここでその数の
領域を1歩踏み出したことになります。
つまり演算とは必ずしも数や行列の演算ばかりではないということです。
また群の例も実に多種多様であることを予感させます。
(さらにS(X)は元の個数が有限な群、有限群であることにも注目してください)
こういうところに数学の自由さを感じるのは僕だけでしょうか?
とにかく、S(X)は写像の合成を演算にして群を成し、S(X)のことをX上の対称群といいます。
特にX={1,2,3、・・・・n}としたときのS(X)をn次対称群といいます。
しかるに、例で説明したX={1,2,3}の場合はS(X)は3次の対称群です。
ところで3次の場合その元の個数は6個、つまり3!個です。
この事は一般化できて、実はn次対称群の元の個数はn!個です。
高校では順列というのやると思います。n個の物を並べ替える方法は確かn!通りありました。
これはS(X)の元の個数にほかなりません。
つまり(3次対称群のところで気が付いたかもしれませんが)S(X)の元を1
つ取ってくることと、1からnまでの順列を1つ定めることは同値なのです。
(同値とは同じ事という意味です)
対称群の説明がだいぶ長くなってしまいました。
ガロアはNO.699 part1で説明した
方程式の根を含む体の拡大列とこの対称群とを
NO.704 part3で説明した同型写像で結びつけることに成功しました。
(もちろん当時はまだまだ数学が創世記にあったため、ガロア自身今とはだいぶ違う表現をしていますが)
ここで部分群について説明しておかなければいけません。
(定義)
Gを群とする。H⊆GがGの部分群であるとはH≠φであって、∀a,b∈H⇒ab-∈Hであ
ることをいう。
実に簡単な定義ですが、数学ではたいていの群が何か大きい群の部分群として現れる
ので、この定義は重要です。
注意してほしいのはa,bをHから取ってきたら、ab∈Hではなくて、
ab‐∈H(aとbの逆元の積)を定義としてあるところです。
この定義さえ満たせば、HはGの演算で群になります。
(つまり群の定義を満たします)これはぜひ確かめてみてください。
牢屋のなかで、ガロアは実に画期的なことを考えます。
S(X)において、Xをn次方程式の根を含む体とし、S(X)の元を同型写像として考えます。
そのときのS(X)を体上の自己同型群といい、AutXと書きます。
(AutXが群になることは証明したので認めてよいでしょう)
そのときこのAutXの部分群とXの中間体(体拡大の列に含まれ
る体で拡大しきった体Xと最小の体も中間体とする)との間に全単射な写像を定めら
れることを、ガロアは示しました。
これはすごいことを言っています。つまり、もし
AutXが有限群ならば、その部分群はもちろん有限個しかないわけでその部分群た
ちと、体拡大の中間体が1つずつ、しかも残りなく対応しているというのですから、
AutXが有限群である以上、それに対応している中間体も有限個しかないというこ
とになります。もっというと例えばAutXの部分群が8個あれば、それに対する中
間体も8個あるということです。ここで、Hを群Gの部分群とすると、{e}とG自
身もGの部分群になっていることは定義から明らかでしょう。ただし{e}は単位元
だけからなるGの部分集合です。
ガロア理論(ガロアが牢屋の中で考えた理論)の本質は上に述べたことです。すなわ
ち、体上自己同型群の部分群と体拡大の中間体の間に全単射が存在する。
(アーベルの考えた事との関係)
5次以上の方程式には根の公式がないというのがアーベルの定理です。
言葉で書いて
しまえばこれだけのことですが、体の概念がなく、群もいわゆる無限群しかなかった
時代にアーベルとガロアは時代を先行しすぎていたことは否めないでしょう。
アーベルの定理の証明は基本的に背理法です。(高校でやるかと思います)つまり、
5次以上の方程式が根の公式を持ったとします。するとその方程式は代数的に解ける
ことになりますのでうまく全ての根を含む定義体の拡大体を作れることになります
が、この議論を進めていくと明らかな矛盾が生じることになるのです。(いまは全て
の体をCの部分体としましょう)
しかし、この証明を完全な形で述べるにはまだまだ
準備不足で、ここでは到底述べることはできません。不本意ですが、この詳しい証明
はあとで時間が許せばやりたいと思います。
ガロアの理論によると、このアーベルの定理を群の言葉を使って翻訳できるというこ
とです。群のほうが体よりは単純な構造を持ちますので、群の言葉を使ってアーベル
の定理を表現した方がわかりやすいと思うかもしれません。しかし数学のみならず、
理論の世界では単純化するのが結構難しい場合もあります。この例も恐らくそうかも
しれません。
実は本当に申し訳ないことに群の言葉を使ったアーベルの定理はまだ準
備不足のためやはり述べられません。ざっと、準備すべきものを挙げるとすれば、同
値関係、正規部分群、可解群、ガロア群などを挙げることができます。しかし、これ
らの概念は正直に言えば、わかりやすく書くことが非常に困難であり、方程式を代数
的に解くことの数学的雰囲気を味わってもらうためには必ずしも必要でない記述をし
なければなりませんから、これ以上深入りしないことにします。
さて、いろいろと不備があるかもしれませんが、なんとかガロア理論の入り口までた
どり着けました。大急ぎでたどり着いた感がありますので、忘れ物が多いですが、後
で補うべきところをじっくり考えて、次回以降に付け足します。

| NO.707 | 2000.1.3. | Junko | 代数方程式の代数的解法(5) |
NO.706 part4にある
(定義)
Gを群とする。H⊆GがGの部分群であるとはH≠φであって、∀a,b∈H⇒ab-∈Hであ
ることをいう。
について考えてみます。
2.単位元について
∀a∈Hについて、aa−∈H、つまり e∈H
3.逆元の存在について
e∈Hですから、∀a∈Hについて、ea−∈H、つまり a−∈H
1.結合律について
∀a,b∈Hについて、b−∈Hなので、
a(b−)−∈H、つまり ab∈H
従って、集合Hはこの演算について閉じていることになります。
集合Hはもちろん集合Gの部分集合ですから、結合律が成り立ちます。
従って、Hは群をなすことがわかります。
逆はもちろんです。

| NO.708 | 2000.1.3. | WAHEI | 代数方程式の代数的解法(6) |
part 5
ここでは少し気分を変えて、「無限について」少し真剣に考えてみましょう。
実際問題として、この世で無限を「見た」人はいるでしょうか?答えはノーです。
(しかし、3歳の時に全盲になったある人は4次元を見ることができるそうです)
でも、無限を「観た」人達は意外と多いです。
我々も数学をやっている以上、この無限からは逃げることはできません。
無限を考えなければ自然数ですら考えることはできません。
自然数は無限にあるのですから。
無限という概念は実際にいろいろなパラドックスを起こす厄介なものですから、きち
んと制御しておかなければなりませんが、よく挙げられるウサギとカメの話で簡単に
説明すると
「ウサギはカメの2倍の速さで走ります。ハンデをつけて、カメがトラックの中間地 点に差しかかったときにウサギが走ることとします。さてウサギがカメのスタート地 点にさしかかった時にはカメはその少し先にいるわけです。そのときのカメの位置を P(1)としましょう。ウサギがP(1)にきた時カメには相当接近していますがまだカメ には追いついていません。カメはP(2)の地点まで進んでいます。(P(1)≠P(2)です) ウサギがP(2)まできたときにはカメはP(2)より先にあるP(3)まで進んでいる。こ のように続いていくと、ウサギはカメに「無限に接近」するがカメに追いつくことは できないことになります」
このように無限という概念(無限大は数ではありません。
従って1/ ∞というのはできません)は意外と扱いが難しいということがわかります。
「理論上無限回の操作を必要とするときどうすればよいか?」
このことについても考えなければならないでしょう。つまり無限集合から、元をすべ
て取り出すには一体どうすればよいでしょうか?
NO.704 part3で紹介した選択公理がその答
えを与えますが、まずは選択公理を噛み砕いた形で述べてみましょう。
(選択公理)
φでない集合が「無限個」並んでいるとする。
それぞれはφでないのでそれぞれから
元をいっせいに取り出して、なにか大きい集合をφでないように作れる。
選択公理とは上のことですが、言っていることは至極もっともなことです。
しかし注意深く扱わなければならないところは[集合が無限個ある]と言うところでしょう。
人間ができる事というのはたとえ機械の力を借りても有限までです。
しかし頭の中で考える以上、たとえ集合が無限に多くあっても空集合でなければ、
それらから元を取ってきて1つの集合にまとめてもいいですよという事をこの公理は保証しています。
ただし1つ1つの集合には1,2,3・・・というように番号が付けられるとしましょう。
(写像の言葉で訳すなら自然数との間に全単射があるということです)
この公理は公理と名前がついている以上証明はないようです。
NO.704 part3で紹介した、
Zorn’s lemmaと整列定理はこの選択公理と同値であることは証明されています。
適当な集合論の本を参考にしてみてください。
この3つ(選択公理、Zorn's lemma,整列定理)がもし認められないというこ
とになれば、これまで積み重ねられてきた数学が一気に崩壊します。
この前証明されたフェルマー予想ももちろん無効になるし、
受験科目としての数学もなくなります。
世の中から、数学というものが考えられなくなるとまでいうのは言い過ぎかもしれま
せんが、もし選択公理がないと、厳密には有限集合しか考えられなくなるので数その
ものの体系がなくなってしまうことになりますからね。
もちろん、今話題にしている代数方程式についても処置無しということになります。
だから、やはりこの3つは代数方程式の代数的解法ともかかわってくる話題です。
選択公理が3つの中では比較的わかりやすいと思って、取り上げてみました。
整列定理もわかりやすいのですが、初めての人に説明すると、簡単なことを難しく定式化し
ているという印象を与えかねませんから、ここでは取り上げないことにしました。僕
よりうまく説明できる人に譲ります。

 E-mail
E-mail
 戻る
戻る