Weekend Mathematics／コロキウム室／テーマ別／35.無限級数の和
| NO.748 | 2000.2.18. | 水の流れ | 無限級数の和（１） |
太郎さんは、数式ソフト「Ｍａｔｈｅｍａｔｉｃａ Ｖｅｒｓｉｎ４」をＷＯＬＦＲＡＭ社から、
先月購入しました。
分からないままに、時間をみながら、使っていましたところ、
次のような無限級数の和を瞬時に求めてくれましたが、
いつも通り、答えに至るまでの過程が全然わかりません。皆さん、教えてください。
問題：
１２＋２２＋３２／２！＋４２／３！＋５２／４！＋・・・
| NO.750 | 2000.2.20. | Junko | 無限級数の和（２） |
私も「mathematica」で計算してみましたら、５eになりました。
こんなにすっきりした値になるには理由がありそうですよね？・・・と考えて・・・わかりました。
まず、ｅｘの級数展開を考えます。
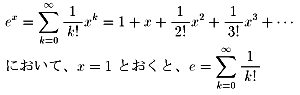
これを使って、問題の級数の値を求めます。
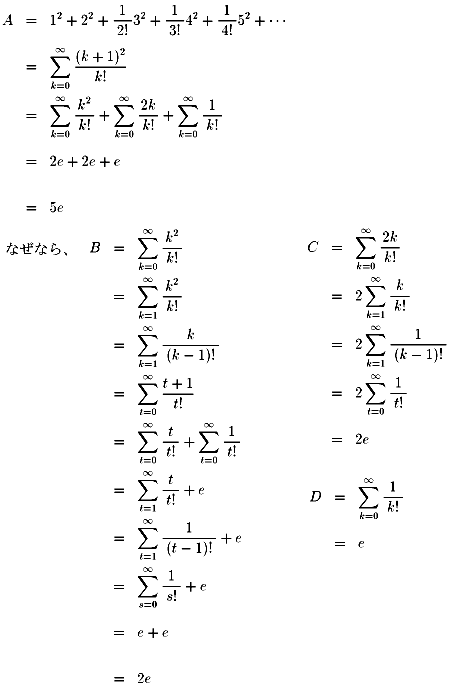
| NO.752 | 2000.2.21. | Junko | 無限級数の和（３） |
前の結果を使いながら、NO.750 無限級数の和（２）でやったのと同じ要領でやっていけば、
順に次数を上げていくことができそうです。
まずは３次式
次は４次式
この調子でいくと、ｎ次式について一般形も導けそうですね。
| NO.753 | 2000.2.22. | 水の流れ | 無限級数の和（４） |
「Mathematica」で分子の次数を上げていきました。
１４次まで上げましたが、１０次までの分を載せます。
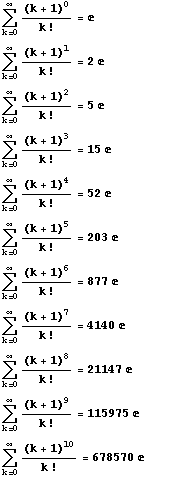
| NO.754 | 2000.2.22. | 水の流れ | 無限級数の和（５） |
| NO.755 | 2000.2.24. | 水の流れ | 無限級数の和（６） |
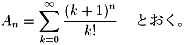
(ただし、ｎ＝０，１，２，３，・・・で、Ａ０＝ｅなる)
ｆ０(x)＝ｅｘとおくと、ｆ’０(x)＝ｅｘ で
ｆ’０(１)＝ｅ
ｆ１(x)＝ｘ ｆ’０(x)＝ｘｅｘとおくと、
ｆ’１(x)＝(１＋ｘ)ｅｘ で ｆ’１(１)＝２ｅ
ｆ２(x)＝ｘ ｆ’１(x)＝(ｘ＋ｘ２)ｅｘとおくと、
ｆ’２(x)＝(１＋３ｘ＋ｘ２)ｅｘ で ｆ’２(１)＝５ｅ
ｆ３(x)＝ｘ ｆ’２(x)＝(ｘ＋３ｘ２＋ｘ３)ｅｘとおくと、
ｆ’３(x)＝(１＋７ｘ＋６ｘ２＋ｘ３)ｅｘ で ｆ’３(１)＝１５ｅ
ｆ４(x)＝ｘ ｆ’３(x)＝(ｘ＋7ｘ２＋6ｘ３＋ｘ４)ｅｘとおくと、
ｆ’４(x)＝(１＋15ｘ＋25ｘ２＋10ｘ３＋ｘ４)ｅｘ で ｆ’４(1)＝５２ｅ
・・・・・ これを同じように繰り返していきますと、
ｆｎ＋１(x)＝ｘ ｆ’ｎ(x)となり、
求める極限値は Ａｎ＋１＝ｆ’ｎ＋１(１) として表される。
さらに、ｆ’ｎ(ｘ)の係数を表にします。
| Ｊ／Ｍ | １ | ２ | ３ | ４ | ５ | ６ | ７ | 計 |
|---|---|---|---|---|---|---|---|---|
| ０ | １ | １ | ||||||
| １ | １ | １ | ２ | |||||
| ２ | １ | ３ | １ | ５ | ||||
| ３ | １ | ７ | ６ | １ | １５ | |||
| ４ | １ | １５ | ２５ | １０ | １ | ５２ | ||
| ５ | １ | ３１ | ９０ | ６５ | １５ | １ | ２０３ | |
| ６ | １ | ６３ | ３０１ | ３５０ | １４０ | ２１ | １ | ８７７ |
| NO.756 | 2000.2.24. | 水の流れ | 無限級数の和（７） |
ｎ個の異なる要素を持つ集合を空でないｋ個の部分集合に分ける方法は何通りありますか
| NO.757 | 2000.2.25. | Junko | 無限級数の和（８） |
NO.752 無限級数の和（３）の続きです。
Ａ０＝ｅ、Ａ１＝２ｅ、Ａ２＝５ｅ、
Ａ３＝１５ｅ、Ａ４＝５２ｅをふまえて、
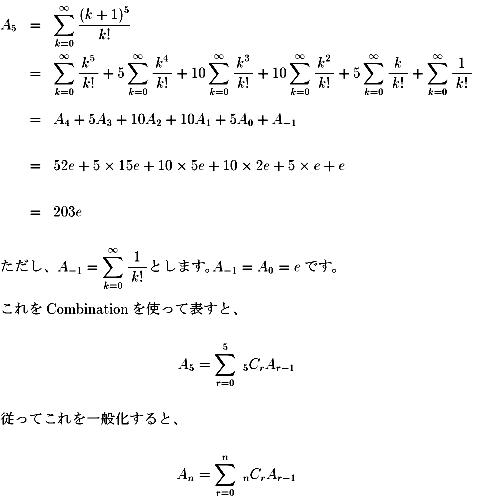
これに沿って、Ａ６を求めてみます。
| Ａ６ | ＝Ａ５＋６Ａ４＋１５Ａ３ ＋２０Ａ２＋１５Ａ１＋６Ａ０＋Ａ−１ |
| ＝２０３＋６×５２＋１５×１５＋２０×５＋１５×２＋６＋１ | |
| ＝８７７ |
調子にのって、もう１つ
| Ａ７ | ＝Ａ６＋７Ａ５＋２１Ａ４＋３５Ａ３ ＋３５Ａ２＋２１Ａ１＋７Ａ０＋Ａ−１ |
| ＝８７７＋７×２０３＋２１×５２＋３５×１５＋３５×５＋２１×２＋７＋１ | |
| ＝４１４０ |
二項展開のような感じで計算できます。
これは、NO.753 無限級数の和（４）で
「水の流れ」さんが計算してくださった結果と一致しています。
| NO.761 | 2000.2.26. | kiyo | 無限級数の和（９） |
表を作りました。
| Ｎ／Ｋ | １ | ２ | ３ | ４ | ５ | ６ | ７ | 計 |
|---|---|---|---|---|---|---|---|---|
| １ | １ | １ | ||||||
| ２ | １ | ２ | ３ | |||||
| ３ | ３ | ３ | １ | ７ | ||||
| ４ | ４ | ６ | ４ | １ | １５ | |||
| ５ | ５ | １０ | １０ | ５ | １ | ３１ | ||
| ６ | ６ | １５ | ２０ | １５ | ６ | １ | ６３ | |
| ７ | ７ | ２１ | ３５ | ３５ | ２１ | ７ | １ | １２７ |
A(n)=SUM{C(n,k)}=2n-1
「水の流れ」さんの問題の趣旨は、
指数関数に関係していると同時に、
階差数列が循環しながら（再帰的に）現れるという点でしょうか？
1 2 3 4 5 6 7 1 1 1 1 1 1 ........................... 1 3 6 10 15 21 2 3 4 5 6 1 4 10 20 35 3 6 10 15 1 5 15 35 4 10 20 1 6 21 5 15 1 7 6
| NO.764 | 2000.2.26. | kiyo | 無限級数の和（１０） |
NO.756 無限級数の和（７）の
「ｎ個の異なる要素を持つ集合を空でないｋ個の部分集合に分ける方法は何通りあり
ますか」
Ｋ個の部分集合の意味を取り違えていました。Ｋ個の要素を持つと勘違いしていました。
これで問題の趣旨が理解出来ました。
同値の問題ですね。
表
| Ｎ／Ｋ | １ | ２ | ３ | ４ | ５ | ６ | ７ | 計 |
|---|---|---|---|---|---|---|---|---|
| １ | １ | １ | ||||||
| ２ | １ | １ | ２ | |||||
| ３ | １ | ３ | １ | ５ | ||||
| ４ | １ | ７ | ６ | １ | １５ | |||
| ５ | １ | １５ | ２５ | １０ | １ | ５２ | ||
| ６ | １ | ３１ | ９０ | ６５ | １５ | １ | ２０３ | |
| ７ | １ | ６３ | ３０１ | ３５０ | １４０ | ２１ | １ | ８７７ |
| NO.766 | 2000.2.27. | kiyo | 無限級数の和（１１） |
表のなかに秘められた美しい規則性について。
表
| Ｎ／Ｋ | １ | ２ | ３ | ４ | ５ | ６ | ７ | 計 |
|---|---|---|---|---|---|---|---|---|
| １ | １ | １ | ||||||
| ２ | １ | １ | ２ | |||||
| ３ | １ | ３ | １ | ５ | ||||
| ４ | １ | ７ | ６ | １ | １５ | |||
| ５ | １ | １５ | ２５ | １０ | １ | ５２ | ||
| ６ | １ | ３１ | ９０ | ６５ | １５ | １ | ２０３ | |
| ７ | １ | ６３ | ３０１ | ３５０ | １４０ | ２１ | １ | ８７７ |
| k | ||||||
| 2 | 1, | 3=1*2+1, | 7=3*2+1, | 15=7*2+1, | 31=15*2+1, | 63=31*2+1 |
| 3 | 1, | 6=1*3+3, | 25=6*3+7, | 90=25*3+15, | 301=90*3+31 | |
| 4 | 1, | 10=1*4+6, | 65=10*4+25, | 350=65*4+90 | ||
| 5 | 1, | 15=1*5+10, | 140=15*5+65 | |||
| 6 | 1, | 21=1*6+15 |
上記の規則性をアピールされたかったのだと思います。
| NO.776 | 2000.3.8. | ヴァ− | 無限級数の和（１２） |
最近 Weekend Mathematics から遠ざかっていたのですけど，
久しぶりに覗いてみると「無限級数の和」という興味深いテーマがあって
楽しんでしまいました．
よく考えると，以前(といってもすごーく前ですが)
私が投稿した
NO.106 プレゼントの問題（１５）
の h(m) が Junko先生の
NO.757 無限級数の和（８）における
Am-1に相当していますね．
「プレゼントの問題」
と「無限級数の和」の一連のお話は
何か関係があるのかもしれませんね．
| NO.777 | 2000.3.9. | 水の流れ | 無限級数の和（１３） |
午後、勤務先で「コロキウム室」の
NO.776 無限級数の和（１２）
の投稿を読んで、大変興味が湧いてきました。
実は”あの第２種スターリング数”の一般項を見つけるもう１つの方法が、
指数型母関数（積率母関数）の登場なのです。
そして、ｋ次の中心積率（モーメント）を定義します。この値をＨ（ｋ）とします。
さらに、特別な原点のまわりのｋ次の積率を出し、この値をh(ｋ)とします。
すると、h(１)＝期待値Ｅ（Ｘ）＝１、Ｈ(２)＝分散Ｖ（Ｘ）＝１となります。
そして、h(ｋ)が何とビル指数となっています。指数型母関数（積率母関数）の定義から導けます。
ここで、確率変数Ｘの指数型母関数（積率母関数）とは、Ｍ（ｔ）＝関数ｅｔｘの
期待値が−ｈ＜ｔ＜ｈ（ｈは正の定数）を満たす原点近傍のすべての実数ｔに対して存在するとき、
Ｍ（ｔ）＝Ｅ［ｅｔｘ］（平均）を言います。
以上は、「新数学辞典」（大阪書籍）から答えています。
さらに、このことは、
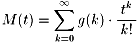
となる予定です。
これが無限級数の和の発展になっていたのです。でも、自信がないです。
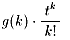の係数がh(ｋ)になっているか確かめていません。これも勉強します。
午後、この示唆をくださったとき、当然太郎さんの胸に熱いもの湧いてきたのは当然でした。
頭の片隅にはこのｋ次のモーメントの言葉がかすかに残っていました。
心のゆとりが欲しい！ ありがとう！ヴァーさん
| NO.787 | 2000.3.18. | 水の流れ | 無限級数の和（１４） |
皆さん！確率密度関数という用語をご存知ですか。
今日は、この話をします。
確率と密度というのは、それほど似かよったものなのでしょうか。
また、確率が密度だとするならば、平均とか分散というのは、
一体にどんな物理量に対応しているのでしょうか。
位置がｘでの密度がｐ（ｘ）であるような質量１の棒を考えてください。
すると、
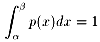
これは（全確率）＝１に相当します。
数学の確率分布とは物理では密度分布といいます。
ｐ（ｘ）は数学ではｘに対応するｙ座標、物理では位置ｘに対応する密度です。
このとき、定積分
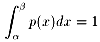
とすると、ｍは数学では平均、物理では、棒の重心の位置を表しています。
すなわち、数学では平均、物理では重心のことです。
また、
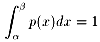
とすると、
σ２は重心を軸に棒を回転したときの「回転質量＝慣性モーメント」を表します。
数学では分散、物理では慣性モーメント＝２次のモーメントです。
詳しく言うと、軸を中心に回転させると、同じ質量の点でも遠くのものの方が、
「重く」感じられる。
正確には軸からの距離の２乗だけ「重く」なるので、各点ごとのこの「重さ」を寄せ集めたものが、
全体の「慣性モーメント」なのです。
例えば、位置ｘの密度がｐ（ｘ）であるコマを考えてください。
分散が小さく、平均からのバラツキが小さいコマは慣性モーメントが小さいので、
フラフラ動きやすく、コマは不安定です。
それに対して、分散が大きく、平均からのバラツキが大きいコマは慣性モーメントが大きいので、
ドッシリト動きにくく、コマは安定しています。
したがって、
NO.776 無限級数の和（１２）
の解決に参考になればと思いまして。
戻る