Weekend Mathematics／コロキウム室／1999.1〜3／NO.49

NO.411　　　　'99 3/20 　　 Junko 　　　ゼーター関数物語（４１）
　　

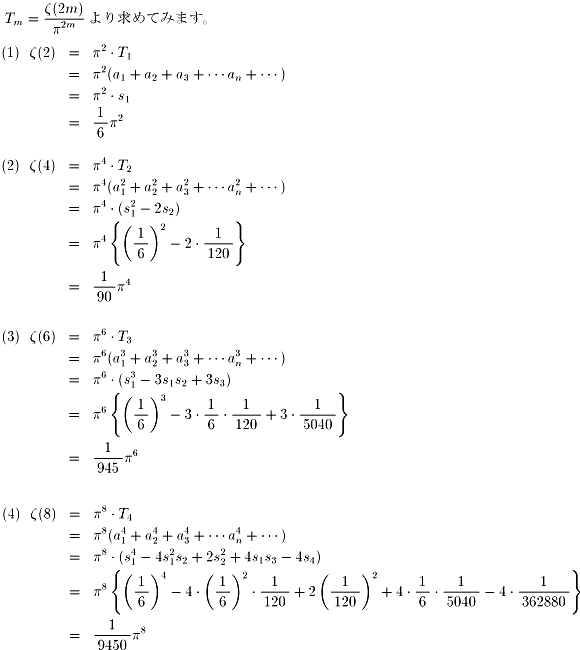
ただ１つ気になることがあります。 それは対称式を基本対称式で表す際の変数の個数です。 無限個に対してもそのままつかっていいものかどうか？

２次のものについて取りあえず帰納法で証明してみました。つまり、
ｓ_(１，ｎ)＝ａ_１＋ａ_２＋ａ_３＋・・・＋ａ_ｎ
ｓ_(２，ｎ)＝ａ_１・ａ_２＋ａ_１・ａ_３＋・・・＋ａ_ｎ−１・ａ_ｎ
Ｔ_(２，ｎ)＝ａ_１^２＋ａ_２^２＋・・・＋ａ_ｎ^２としたとき、
Ｔ_(２，ｎ)＝ｓ_(１，ｎ)^２＋２ｓ_(２，ｎ)を仮定し、
Ｔ_{(２，ｎ＋１)}＝ｓ_{(１，ｎ＋１)}^２＋２ｓ_{(２，ｎ＋１)}を示すわけです。

実際の証明はここでは省略しますが、さほどむずかしくはないのでやってみてください。 同様に３次、４次・・・などでも証明できそうです。

しかしそれにしても有限での話です。 無限の場合も成り立ちそうだとは思うのですが・・・ 無条件に使っていいものかどうか、疑問です。

ゼ−タ−関数の値に限っていえば、上述の等式をすべて有限でかいておいて、 最後に極限をとればいいのかなと思います。

NO.412　　　　'99 3/20 　　 Junko 　　　ゼーター関数物語（４２）
　　

NO.409を真似して、５次の対称式に挑戦してみました。

ｓ_１＝ａ＋ｂ＋ｃ＋ｄ＋ｅ
ｓ_２＝ａｂ＋ａｃ＋ａｄ＋ａｅ＋ｂｃ＋ｂｄ＋ｂｅ＋ｃｄ＋ｃｅ＋ｄｅ
ｓ_３＝ａｂｃ＋ａｂｄ＋ａｂｅ＋ａｃｄ＋ａｃｅ＋ａｄｅ＋ｂｃｄ＋ｂｃｅ＋ｂｄｅ＋ｃｄｅ
ｓ_４＝ａｂｃｄ＋ａｂｃｅ＋ａｂｄｅ＋ａｃｄｅ＋ｂｃｄｅ
ｓ_５＝ａｂｃｄｅとして、

Ｔ_５＝ａ^５＋ｂ^５＋ｃ^５＋ｄ^５＋ｅ^５を ｓ_１・・・ｓ_５で表します。

次数の関係から、

Ｔ５＝ｓ１５＋Ａｓ１・ｓ２２＋Ｂｓ１２・ｓ３＋Ｃｓ１・ｓ４＋Ｄｓ１３・ｓ２＋Ｅｓ２・ｓ３＋Ｆｓ５とおきます。

• (１，１，０，０，０)を代入して、１５＋Ａ＋４Ｄ＝０
• (１，１，−１，０，０)を代入して、Ａ−Ｂ−Ｄ＋Ｅ＝０
• (１，１，１，０，０)を代入して、８０＋９Ａ＋３Ｂ＋２７Ｄ＋Ｅ＝０
• (２，−１，−１，０，０)を代入して、Ｅ＝−５
• (１，１，１，−１，０)を代入して、１５−４Ｂ−Ｃ＝０
• (１，１，１，−１，−１)を代入して、４Ａ−２Ｂ＋Ｃ−２Ｄ＋４Ｅ＋Ｆ＝０

Ｔ５＝ｓ１５＋５ｓ１・ｓ２２＋５ｓ１２・ｓ３−５ｓ１・ｓ４−５ｓ１３・ｓ２−５ｓ２・ｓ３＋５ｓ５となります。

これをもとに、ζ(１０)の値を計算してみます。

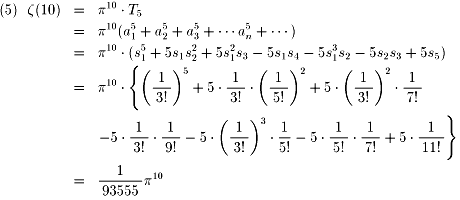
と結果をかいてしまえば簡単ですが、これを手計算するには気力と根気が必要でした。 しかも私は「mathematica」で結果を確認できますが、もちろんそんなものはない時代に ζ(２６)まで計算したオイラ−という人は、想像すらできません。

NO.413　　　　'99 3/21 　　 水の流れ 　　　ゼーター関数物語（４３）
　　

ゼーター関数ζ（２）物語第１2夜の始まり、始まり。
皆さんはゼーター関数ζ（２）、ζ（４）、ζ（６）、ζ（８）の値を 実際に求めたことでしょう。
ここで、確かめておきましょう。
ζ（２）／π^２＝１／６
ζ（４）／π^４＝１／９０
ζ（６）／π^６＝１／９４５
ζ（８）／π^８＝１／９４５０
・・・となります。計算に自信のある人はζ（１０）以降に取り組んでください。

さて、数学的センスのある皆さんは有限個の文字について、

ａ１２＋ａ２２＋ａ３２＋ａ４２＋・・・＋ａｎ２

　　＝（ａ１＋ａ２＋ａ３＋ａ４＋・・・＋ａｎ）２−２（ａ１・ａ２＋ａ１・ａ３＋・・・＋ａｎ−１・ａｎ）

Ｔ２＝ａ１２＋ａ２２＋ａ３２＋ａ４２＋・・・＋ａｎ２＋・・・
　
　　＝(ａ１＋ａ２＋ａ３＋ａ４＋・・・＋ａｎ＋・・・）２−２（ａ１・ａ２＋ａ１・ａ３＋・・・＋ａｎ−１・ａｎ＋・・・）

このようにして、４乗の逆数の和に関する素敵な答えを発見したことになります。 ですからオイラーは新しいオモチャを見つけた子供ように嬉々として、 次々に求め、ついにはζ（２６）の値という驚異的なところまで 偶数の指数を試していったのです。
いうもでもなくここまでに至る数学の小道を探索してみた者は 歴史上一人もいませんでした。

ところで、一つ疑問がすぐに頭に浮かんできます。 奇数のベキ乗を持つ整数の逆数の和はどうでしょう？
たとえば、１＋１／８＋１／２７＋１／６４＋・・・ のような級数も同じように計算値が出せるでしょうか？ 問題の和が任意の分数ｐ／ｑに対して（ｐ／ｑ）π^３ といった形になるのではないかと推測するのは簡単ですが、 今に至るまでこの推測が正しいかどうかは誰にも分かっていません。
いずれにしても、この素晴らしい和のすべてはその後、 今日のより高い理論的に厳密な証明によって確認されています。

ゼーター関数ζ（２）物語を投稿するようになって、 「数学の美しさ、不可思議さ、広大さ、自由さ、偉大な数学者の心の動き」 に触れることができ、理解できたという幸福感に慕っています。
この物語に答えを寄せてくださいました多くの読者のみなさんありがとうございます。

この物語のきっかけはやはり、次の問題です。
今度は「２つの自然数を任意にとるとき、 これらが互いに素である確率を求めよ」にチャレンジしていきます。 それでは、ゼーター関数ζ（２）物語第１2夜の終わりとします。

NO.414　　　　'99 3/21 　　 月の光 　　　ゼーター関数物語（４４）
　　

NO.403を受けて

一方は有理数、もう一方は無理数の無限積なのに 同じ値になるというのは面白いと思います。

NO.415　　　　'99 3/22 　　 水の流れ 　　　ゼーター関数物語（４５）
　　

ゼーター関数ζ（２）物語第１３夜＜特別寄稿＞の始まり、始まり。

さて、レオナルド・オイラーは広範囲に業績を残した １８世紀を代表する数学者であります。 この物語の一部は、１７４８年に発表された 『無限小解析入門』の中に書いてあります。
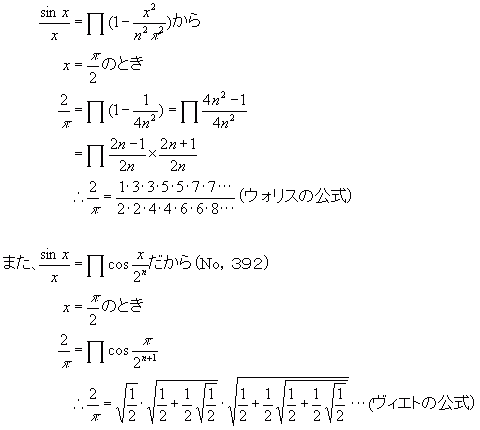
また、オイラーの数学について語ろうとすると、 いずれにしても彼の論文の全集「オペラ・オムニア」全７３巻にふれないわけにはいきません。 これは彼が生涯に著した８８６篇にもおよぶ論文 （ラテン語、フランス語、ドイツ語などさまざまな言語で書かれています）をおさめたものです。 作品の幅は広く、相当なものでしたから、未発表のまま残されていたものを出版するのに 死後４７年間もかかったと言われています。
それらには偏微分からグラフ理論、複素解析、常微分方程式に至るまで 数学の全領域にそれぞれ新しい方向を示した独創性あふれる論文が入っているのです。 実際、あらゆる数学の分野にオイラーに帰される重要な理論が存在します。
したがって私たちはオイラー定数、オイラーの多項式、オイラー積分等々の存在は もちろん、幾何学ではオイラーの三角形、位相幾何学では、オイラーの標数、グラフ 理論ではオイラーの閉路といった具合にあちこちでその名を見出すことになります。

ここで、「数学の知性」を読んでいて、興味深い問題がありましたので、 紹介します。
それは、ヨハン・ベルヌーイが１６９６年７月にライプニッツの雑誌 “ActaEruditorum”に手強い問題を発表しました。ヨハン自身こう述べています。
『気高く、独創的な精神は知識を増やすための努力を引き出すものであるが、 これを強く刺激するものとしては、難解でしかも役に立つ問題を求め、 これを解くことで名声を獲得し後世に永遠の記念塔を残すこと・・・、 これ以上のものはほとんど考えれない。それは周知のことである。』
ヨハンの考え出した特別問題は大変良い問題でした。

彼は異なる高さにある２点を考えます。 この２点をＡ，Ｂとし、１点がもう１点の真上にないものとします。 これらの２点を結ぶ直線から円弧、波形に曲がりくねったものまで、 もちろん無数にあるわけです。 そこで、この曲線にそってＡからＢへボールを転がし落とすと想像してみて下さい。 ボールが上の点から下の点にたどり着くまでにかかる時間は当然、 曲線の形に関わってくることになります。 ベルヌーイはボールが最も短い時間で転がり落ちる特定の曲線ＡＢを求めよという問題を出して、 数学界に挑戦したのです。 彼はこの曲線をギリシャ語の“最短”と“時間”という語からとって最速降下問題と呼びました。

明らかに最初に考えつくことはＡとＢを結ぶ直線とすることですが、 ヨハンは軽率な判断を未然に防ぐために言っておこう。 実際Ａ点からＢ点を結ぶ最も短い距離は直線ＡＢであるが、 しかしこれは最も短い時間で動く道ではないのである。 私がその曲線ＡＢに与える名称は幾何学者にはよく知られているものである。

ヨハンは数学界に対し解を受け付ける期限を１６９７年１月１日としました。 しかし期限がきたとき彼は１つの解とともに“敬愛なるライプニッツ” から手紙を受け取りました。 ライプニッツは期間が短すぎるとの不公平がでないように当分の間この問題は公開し ておいて、次のイースターまで期限を延ばしたらどうだろう？と丁寧に申し出ました。

さーて、今夜は長ーくなりましたね。 目をこすりながらでもいいですから、最後まで読んで下さい。 皆さんもこの最速降下問題の曲線の名称を考えてください。 答えだけで良いです。 次の夜は本題に入ります。お休みなさい・・・。　

NO.416　　　　'99 3/23 　　 水の流れ 　　　ゼーター関数物語（４６）
　　

ゼーター関数ζ（２）物語第１4夜の始まり、始まり。

震え上がるような、数の神秘を知るために、 オイラーは生涯数学の研究に余念がありませんでした。 ゼーター関数ζ（ｓ）の値をｓ＝２６まで、求めています。 ここで、その値を紹介します。

ζ（１０）＝（１／９３５５５）π^１０
ζ（１２）＝（１／６３８５１２８７５）π^１２
ζ（１４）＝（２／３^６・５^２・７・１１・１３）π^１４
・・・・・・
ζ（２６）＝（１３１５８６２／１１０９４４８１９７６０３０５７８１２５）π^２６

さて、第１２夜に、「２つの自然数を任意にとるとき、 これらが互いに素である確率を求めよ」と書きました。 題意をはっきりさせます。 任意の２つの自然数は同じであっても 良いですし、（１，１）の組は互いに素とします。 もちろん、（２，２）は互いに素とはいいません。

ここで、任意の２つの自然数の組を（ｘ、ｙ）とします。
コロキウム室NO.263、NO.270、 NO.289を見て下さい。

1. １≦ｘ≦１０，１≦ｙ≦１０のとき、互いに素の組は１００組中６３個あります。
2. １≦ｘ≦１００，１≦ｙ≦１００のとき、 互いに素の組は１００００組中６０８７個あります。
3. ・・・

このゼーター関数物語を投稿していた３月上旬に、 「数学セミナー３月号」に偶然にも、同じ問題がありました。 これは天の声といった驚きでした。
＜教えて頂いた天使さん！ありがとうございます。＞

そこで、今夜の問題です。

1. １つの自然数を任意にとるとき、素数ｐの倍数である確率を求めよ。
2. ２つの自然数を任意にとるとき、ともに素数ｐの倍数である確率を求めよ。
3. ２つの自然数を任意にとるとき、この公約数が素数ｐとならない確率を求めよ。
4. ２つの自然数を任意にとるとき、これらが互いに素である確率を求めよ。

NO.417　　　　'99 3/23 　　 Junko 　　　不思議な級数（３）
　　

有限なものについては、交換法則、結合法則が成り立ちますが、 無限級数を扱う際には足していく順序を変えたり、 変則的な足し方をするのは危険だということですね。
NO.386とNO.389の 両方にでてくる、調和級数1+1/2+1/3+1/4+･･･は無限大に発散することが わかっています。 (NO.343、NO.346、NO.357など)
収束しないものを足したり、ひいたりすることはできません。 特に、NO.389の式（２）は 「＋∽−∽」となっていていわゆる不定形ですから「＝０」はまずいわけです。

NO.418　　　　'99 3/23 　　 水の流れ 　　　大相撲春場所優勝決定戦（１）
　　

大相撲春場所１０日目を終わって、 ５人の力士が２敗で混沌としたダンゴレースの様相です。 優勝力士が誰になるか、興味が出てきました。
そこで、千秋楽を終わって、平成８年九州場所のように、 ５人の力士Ａ，Ｂ，Ｃ，Ｄ，Ｅで優勝決定戦を行うことになりました。 対戦方法は最初、ＢとＣ、ＤとＥがくじで引いて、対戦します。 Ａは不戦勝です。このあと、いわゆるともえ戦に入ります。
ここで、ともえ戦とは順次に戦い、他の２人を最初にごぼう抜きした 力士が優勝することです。 勿論、５人の力士の実力は同じとして、分かり易くするために、 最初に戦ったＢとＣの勝者をＦ、次に戦ったＤとＥの勝者をＧとします。

ここから、次の２つの順序でともえ戦を対戦します。 ５人それぞれの優勝する確率を求めてください。

1. 最初にＡとＦが対戦し、その勝った力士とＧが戦い、 他の２人を最初にごぼう抜きするまで、戦い続ける。
2. 最初にＦとＧが対戦し、その勝った力士とＡが戦い、 他の２人を最初にごぼう抜きするまで、戦い続ける。

NO.419　　　　'99 3/24 　　 豊作 　　　定義域（１０）
　　

NO.420　　　　'99 3/28 　　 Junko 　　大相撲春場所優勝決定戦（２）
　　

(1)勝った力士の表を書きます。
連続２勝しないと優勝できませんので、永久に続く可能性もあるわけです。

これを利用して、それぞれ優勝する確率を求めてみます。

Ａが有利なのはもちろんですが、 先に試合を始められる分だけＧよりＦの方が有利ですね。

(2)同じように勝った力士の表を書きます。

(1)よりも(2)の方が、不公平が緩和されているようですが、 やはりＡ(最初の不戦勝)が有利です。

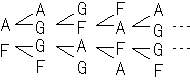
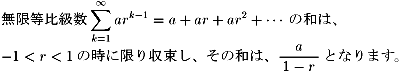
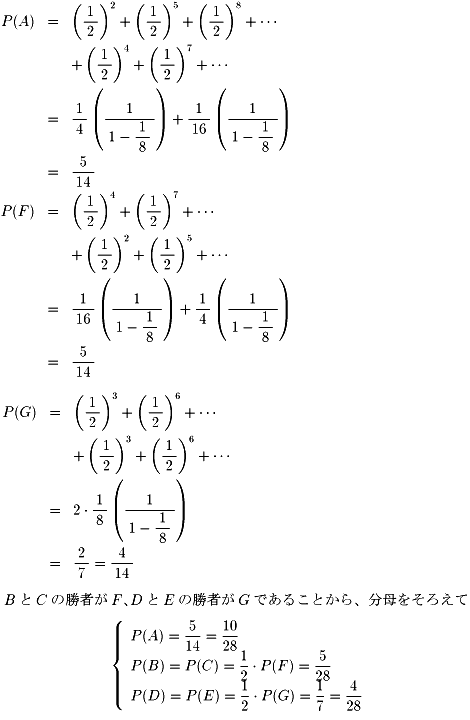
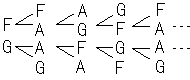
E-mail 戻る