Weekend Mathematics／コロキウム室／1999.1〜3／NO.33

NO.254 　　　 '99 1/3 　　Idaho Potato 　　　 分数の問題・その後（４）

定理：任意の分数(正確に言うと正の有理数)は 必ず異なる単位分数の和として表すことができる

を証明するのに、

補題1：与えられた分数を超えない単位分数の中で一番大きいものを 引いていきます。これを何回か繰り返すと、必ず残りも単位分数になります。

を証明して、その系として定理が得られる、としていますが、 実はそれでは不十分であることに気づきました。

補題1の証明に含まれている仮定のうち、 「b＜a」は証明の中で使われていないので、 補題1自体は、与えられた分数が1以上であっても成り立ちます。
また、与えられた分数が2未満の場合には、 同じ単位分数が高々1度しか使われないことは、容易にわかります。
しかし、与えられた分数が2以上の場合は、 補題1によって与えられるアルゴリズムで単位分数に分解しようとすると、 1を複数回使うことになってしまいます。

定理の正しい証明を与えるには、次のように議論を修正すればOKです。

次の有名な事実を使います。

命題：調和級数 1 + 1/2 + 1/3 + ... は、正の無限大に発散する。

これは、次のように言い換えることができます。

補題2：任意の正の実数 x について、
1 + 1/2 + 1/3 + ... + 1/n > x
となる自然数 n が存在する。

さて、与えられた正の有理数を x とします。
この x について、補題2を満たす自然数 n のうち最小のものをとります。
このとき、y = x - ( 1 + 1/2 + 1/3 + ... + 1/(n-1) ) とおくと、
n の選び方により、 0 <= y < 1/n が成り立ちます。
この y を、補題1で与えられるアルゴリズムで単位分数の和に分解すると、 そこには、1/n 未満の単位分数しか現れないので、 1, 1/2, 1/3, ..., 1/(n-1) とは重複しません。
つまり、最初に与えられた x から、1, 1/2, 1/3, ... というふうに、 単位分数を大きいほうから順に引いていくと、 補題2によって、どこかでそれが続けられなくなりますが、 そのときの「余り」について、補題1を使えばよいわけです。

NO.255 　　　 '99 1/3 　　ちょま 　　　 １９９９年の問題（２）

１９９９年の問題を考えてみました。
３４、３８が出来ていませんが、１から４０までです。

１＝−１−９÷９＋√９	２＝−１＋√９＋９−９
３＝１＋√９−９÷９	４＝１＋√９＋９−９
５＝１＋√９＋９÷９	６＝１×９−９÷√９
７＝−１＋９−９÷９	８＝−１＋９＋９−９
９＝１×９＋９−９	１０＝１＋９＋９−９
１１＝１×９９÷９	１２＝１＋９９÷９
１３＝１９−９＋√９	１４＝−１＋９＋９−√９
１５＝１×９＋９−√９	１６＝１＋９＋９−√９
１７＝−１−９＋９×√９	１８＝１９−９÷９
１９＝１９＋９−９	２０＝１９＋９÷９
２１＝１×９＋９＋√９	２２＝１９＋９÷√９
２３＝−１＋９×√９−√９	２４＝１×９×√９−√９
２５＝１９＋９−√９	２６＝−１＋９＋９＋９
２７＝１×９＋９＋９	２８＝１＋９＋９＋９
２９＝−１＋９×√９＋√９	３０＝１×９×√９＋√９
３１＝１９＋９＋√９	３２＝（１＋√９）×（９−’９）
３３＝（１＋√９）×９−√９	３４＝？
３５＝−１＋９×√９＋９	３６＝１×９×√９＋９
３７＝１９＋９＋９	３８＝？
３９＝（１＋√９）×９＋√９	４０＝（１＋√９）×（９＋’９）

なるべく使う記号を少なくしようと１から３１までは＋−×÷√のみで作りました。
３２と４０の　’９　は、本当は９の上に点をうつ循環小数のつもりで、’９＝１　 です。
４１以降も考えているんですが出来ていないところが多いです。 他の記号を使えばかなり出来そうですが・・・

NO.256 　　　 '99 1/4 　　月の光 　　　 オリジナル問題（１）

オリジナル問題。

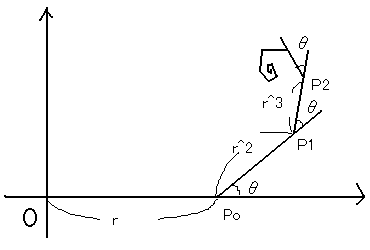
問題)ＸＹ平面で、Ｘ軸上にＰ₀(ｒ，０)をとる。ただし0＜r＜1。
次に、Ｐ₀をθだけ回転し、 長さをr倍した点をＰ₁とする。
つまりＰ₁は
(ｒ＋ｒ²ｃｏｓθ，ｒ²ｓｉｎθ)
このとき、ｌｉｍＰ_n(n→∽)を求めよ。

0＜θ＜πの条件は必要ないですね。消します。(1/5)

NO.257 　　　 '99 1/4 　　ちょま 　　　１９９９（２）

NO.247 　１９９９　を考えてみました。
３つ作ってみました。
１２×３４×５−６×７−８＋９＝１９９９
１２×３４×５＋６−７×８＋９＝１９９９
−１＋２３４５−６×７×８−９＝１９９９

ところで、最初の２つをみくらべると６、７、８のところの演算子が違うだけで、 とてもよく似ています。 ３つの連続している数Ａ、Ｂ、Ｃには
Ａ×Ｂ＋Ｃ＝−Ａ＋Ｂ×Ｃ
の関係が成り立っているようです。
Ｂ＝ｎとおいて左辺と右辺を計算してみると、

左辺＝（ｎ−１）×ｎ＋（ｎ＋１）
　　＝ｎ×ｎ−ｎ＋ｎ＋１
　　＝ｎ２＋１
右辺＝−（ｎ−１）＋ｎ×（ｎ＋１）
　　＝−ｎ＋１＋ｎ×ｎ＋ｎ
　　＝ｎ２＋１
ゆえに　左辺＝右辺

となり、Ａ×Ｂ＋Ｃ＝−Ａ＋Ｂ×Ｃが成り立っていることがわかります。

ちなみに４つ連続している数Ａ、Ｂ、Ｃ、Ｄには
　　　　Ａ＋Ｂ＋Ｃ＋Ｄ＝−Ａ×Ｂ＋Ｃ×Ｄ
が成り立っています。
Ｂ＝ｎとおいて左辺と右辺を計算してみると、

左辺＝（ｎ−１）＋ｎ＋（ｎ＋１）＋（ｎ＋２）
　　＝４ｎ＋２
右辺＝−（ｎ−１）×ｎ＋（ｎ＋１）×（ｎ＋２）
　　＝−ｎ２＋ｎ＋ｎ２＋ｎ＋２ｎ＋２
　　＝４ｎ＋２
ゆえに　左辺＝右辺となります。

たとえば連続している数１、２、３、４ならば
　　　　１＋２＋３＋４＝−１×２＋３×４＝１０
というわけです。

演算子がちがうのに同じ数字から同じ計算結果になるのがおもしろいと思います。

NO.258 　　　 '99 1/5 　 　水の流れ 　　　オリジナル問題（２）

NO.259 　　　 '99 1/5 　　ちょま 　　　 １９９９年の問題（３）

NO.246　１９９９年の問題の ３４、３８が出来ました。
９９÷√９＝３３を使えば３２、３３もさらにシンプルに 表せます。

３２＝−１＋９９÷√９

３３＝１×９９÷√９

３４＝１＋９９÷√９

３８＝１９×（’９＋’９）

NO.260 　　　 '99 1/5 　　月の光 　　　 互いに素（１）

任意に自然数を２つ選ぶ時、それらが互いに素である確率を求めよ。

NO.261 　　　 '99 1/7 　　マサボー 　　　 分数の問題・その後（５）

この問題を考える時、答えを求める他に次の２点にも 注目する必要があると思います。
それは、１）任意の分数（正の有理数）は単位分数の和として 表わすことが出来る、
２）その表わし方は無限に存在する、の２点です。
これらの提議は解答の中で証明されていると思いますが、 では実際の答えを示すにあたり （今回の問題は２／３や４／５を単位分数の和で表わすこと）、 数学的に正しい解答を書くのはかなり難しいかったのではないでしょうか （当然、答えが無限にある訳ですから）。
私が思うに数学は普遍性を重んじる学問ですから、 ある一定のプロセス（あるいは公式）を踏むことで 全ての答えが得られることが重要であり、 答えに「もれ」があってはならないと思います。 その意味から「水の流れ」さんの答えはかなり正解に近いものでしょう。
別のアプローチとして最初に方程式にて最少の単位分数の数を決め、 次に（最少＋１）の単位分数の場合、 （最少＋２）の単位分数の場合を各々方程式で求めるのも 答えを漏らさない方法の一つだと思います。
しかし、最初から最少の単位分数の個数を決める方法がない場合は （私には分からなかった）、２個の場合、３個の場合と 「しらみ潰し」でやるしかないのかもしれません。
やはり数学も科学であり99%のperspirationが必須なのでしょう。

NO.262 　　　 '99 1/7 　　Junko 　　　 年号と西暦の関係（２）

明治をＭ、大正をＴ、昭和をＳ、平成をＨ、西暦をＸとすると、 次の関係が成り立ちます。
Ｘ＝Ｍ＋１８６７（１≦Ｍ≦４５）
Ｘ＝Ｔ＋１９１１（１≦Ｔ≦１５）
Ｘ＝Ｓ＋１９２５（１≦Ｓ≦６４）
Ｘ＝Ｈ＋１９８８（１≦Ｈ≦１１）

次に素数の探し方です。
「エラトステネスのふるい」というのを紹介しましょう。

• まず、１からＮまでの表を作ります。 １は素数とは言いませんから、消します。
• ２は素数ですから○で囲み、２の倍数をすべて消します。(素数ではないからです。)
• 次に３は素数ですから○で囲み、３の倍数をすべて消します。(同様に素数ではないからです。)
• ４は既に消えています。
• ５は素数ですから○で囲み、５の倍数をすべて消します。
• 以下同様にしていくと、素数だけが○で囲まれた状態で残ります。

試しに、１から１００までをふるいにかけてみました。

(素数は○で囲む替わりに、赤くしてあります。)

１	２	３	４	５	６	７	８	９	１０
１１	１２	１３	１４	１５	１６	１７	１８	１９	２０
２１	２２	２３	２４	２５	２６	２７	２８	２９	３０
３１	３２	３３	３４	３５	３６	３７	３８	３９	４０
４１	４２	４３	４４	４５	４６	４７	４８	４９	５０
５１	５２	５３	５４	５５	５６	５７	５８	５９	６０
６１	６２	６３	６４	６５	６６	６７	６８	６９	７０
７１	７２	７３	７４	７５	７６	７７	７８	７９	８０
８１	８２	８３	８４	８５	８６	８７	８８	８９	９０
９１	９２	９３	９４	９５	９６	９７	９８	９９	１００

また、特定の数Ｎが素数かどうかを判断するにはどうしたらいいか？
２，３，５，７，・・・と素数だとわかっている数で割っていきます。 もし何かで割り切れれば、もちろん素数ではありません。 (素数でないものを合成数といいます。)
√Ｎまで調べて、割り切れるものがなければ、それは素数ということになります。
なぜ√Ｎで充分か？
もし、√Ｎより大きい数Ａで割れるならば、Ｎ＝ＡＢとなり、 このときＢ＜√Ｎとなります。 ですから、先に√Ｎより小さい数Ｂで割り切れているはずだからです。

NO.263 　　　 '99 1/6 　　水の流れ 　　　 互いに素（２）

自然数Ｎ＝ａ^αｂ^βｃ^γ・・・ （素因数分解した形）とおくと、
Ｎと互いに素（１以外に公約数をもたない）なものの個数をψ（Ｎ）と表す （オイラー関数）。

E-mail 戻る