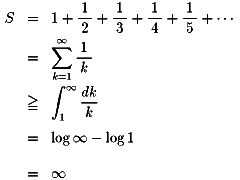
この証明はあっているかどうか自信はありません。 シグマから積分に変形しているあたりが怪しいです。
Weekend Mathematics/コロキウム室/1999.1~3/NO.42
NO.346 '99 2/19 みや ゼーター関数物語(6)
調和級数が発散することの証明です。
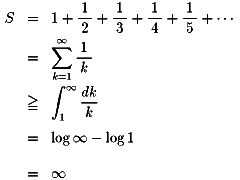
この証明はあっているかどうか自信はありません。
シグマから積分に変形しているあたりが怪しいです。

NO.347 '99 2/20 水の流れ 極と極線(4)
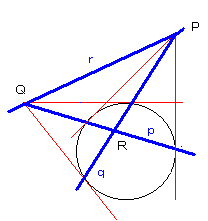 junko さんが発見されたように、
dD=r2は成り立ちます。
junko さんが発見されたように、
dD=r2は成り立ちます。
これより、点Pが与えられたときは、点Mの位置が決まります。
ただし、原点からの距離がdで、直線OPに垂直である点をMとする。
ゆえにそのMを通り 直線OPに垂直な直線pが点Pの極線である。
逆に、極線が与えられると、
dD=r2の関係を保つような点すなわち、
極を決定できます。
注意として、円の中心の極線は無限遠の直線で、
中心を通る直線の極は無限遠の点である。
さて、極と極線の相反性 の話をします。
円:x2+y2=r2・・・① に関する
点P(x1、y1)の極線pの方程式は
x1x+y1y=r2 である。
p上にある任意の1点Q(x2,y2)をとれば、
x1x2+y1y2=r2 ・・・ ② となる。
また、Qのこの円に関する極線qの方程式は
x2x+y2y=r2 であるから、
② は点Pがq上にあることを示しています。
よって、「1つの円に関して1点Pの極線が他の1点Qを
通るとき、この円に関してQの極線はまたPを通る」
このことを 極と極線の相反性 と言います。
また、このような性質をもつ2点、P、Qをその円に関する共役な点という。
さらに、1つの直線pの円①に関する極をPとすればPを通る任意の
直線qのの円①に関する極をQは、必ずp上にあることがわかる。
このような性質をもつ2直線p、qを、その円に関して互いに共役な直線という。
また、pとqとの交点をRとすれば、ここで、<図参照>
直線PQはRの極線である。
だから△PQRの各頂点のこの円に関する極線は、
ちょうどその対辺になっています。
このような三角形を自己共役三角形といいます。
<参考文献:新数学事典 大阪書籍>
さて、この問題では、点P(3,2)を通る任意の2本の
直線AB,CDを引いて、直線ABが極線となるような極をMとする。
直線CDが極線となるような極をNとすると、
直線MNが点Pの極線となります。
これが3x+2y=16 なのです。

NO.348 '99 2/20 Junko ゼーター関数物語(7)


NO.349 '99 2/20 Weadore 2000年問題?(1)
X = 1999/2-1998/3+1997/4-・・・・・・-2/1999+1/2000
Y = 1/1001+3/1002+5/1003+・・・・・・+1999/2000
とする。
このときXとYとの大小関係を示せ。

NO.350 '99 2/21 Junko ゼーター関数物語(8)
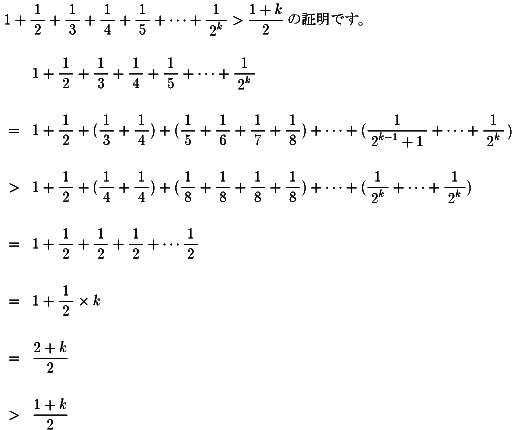

NO.351 '99 2/21 水の流れ ゼーター関数物語(9)
「ゼーター関数ζ(2)物語第4夜の始まり、始まり。
昨夜、こんな問題を出したままでしたね。
『任意の整数をkとして、
1+1/2+1/3+1/4+・・・+1/2k>(k+1)/2』
皆さん、ニコル・オレスムと同じ証明になるでしょうか?
もし、そうなら数学的真理の普遍性を実感します。
実は、ニコル・オレスムの証明と同じことが、6世紀後でも、
「Junko」さんが
NO.343で証明しています。
数学的真理の神秘に驚いています。
さて、ヨハン・ベルヌーイはもう1人の数学者イタリアの
ピエトロ・メンゴーリにも先を越されています。
メンゴーリの証明は1647年、ベルヌーイの証明の40年
ほど先立つものでした。
これは実にシンプルな証明ですが、まず最初に前提になる定理が出てきます。
第4夜の問題です。皆さん、解いてみてください。
『任意の整数をkとして、
1/(k-1)+1/k+1/(k+1)+>3/k である』
この定理は3個の連続する整数の逆数を足したとき、
その和は真ん中の数の逆数の3倍より大きいという問題です。
これが、メンゴーリが1647年に行った短い証明の
中で調和級数への挑戦に必要な定理でした。」

NO.352 '99 2/21 Weadore 1999!の桁数(6)
NO.340の解答です。
1999!/10nの末尾の0の桁数は1999!に含まれる
5の因数を数えれば良い。
∴[1999/5]+[1999/52]+[1999/53]+[1999/54]=399+79+15+3=496
ここで、[ ]はガウス記号である。
よってnの最大数は496である。
1999!/10496の一の位はまず、1999!のほうが10496より
2の因数を多く含んでいるので、一桁目は偶数。
つまり、2,4,6,8のどれかである。
ここから周期性(数列)から求める事もできるが、
(ちなみに僕は数学オリンピック当日はそれで求めた)
ここでは、合同式を使って示す。
まず、
1999! = 50(1×2×3×4×6×・・・・・・×1999)
×5399(1×2×3×4×6×・・・・×399)
×579(1×2×3×4×6×・・・・・×79)
×515(1×2×3×4×6×・・・・・×14)
×53(1×2×3)
∴ 2496×(1999!/10496)
≡(1×2×3×4×6×7×8×9)249×(2×3×4×2×3)(mod 10)
≡6249×4(mod 10)
≡6×4(mod 10)
≡4(mod 10)
また、2496= (24)124
≡6124(mod 10)
≡6(mod 10)
∴1999!/10 ≡ 4 or 9(mod 10)
NO.353 '99 2/22 Junko 宇宙空間での最短経路問題(2)
NO.313で、
立方体の8つの頂点を最短で結ぶにはどうしたらよいかという問題が
提示されています。

実験してみました。
ストロ-の中に糸を通して立方体(正六面体)を作り、
それをシャボン液にひたします。
そして静かに引き上げると、写真のような状態になります。
中央に、シャボン液による立方体ができています。
不思議ですよね?

ついでなので、正四面体も作ってみました。
写真だとわかりづらいのですが、
中心に向かって二等辺三角形の膜が6枚張られます。
結構きれいにできるので、感動します。
正八面体もやってみました。中に菱形のような膜ができて、
これもまたきれいです。
なかなかうまく写真に撮れないので、これは是非実験してみてください。
用意するものは、ストロ-と糸とシャボン液。
すぐにできますから、是非やってみてください。
楽しいです。

NO.354 '99 2/22 Junko 2000年問題?(2)


NO.355 '99 2/22 みや ゼーター関数物語(10)
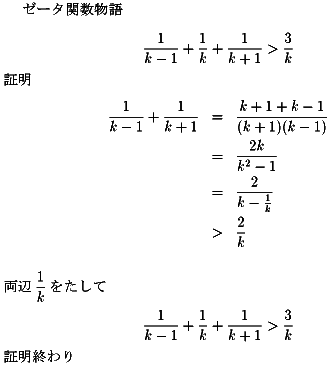

NO.356 '99 2/22 Junko ゼーター関数物語(11)


 E-mail
E-mail
 戻る
戻る