Weekend Mathematics/コロキウム室/1999.1〜3/NO.34
コロキウム室
NO.264 '99 1/8 月の光 富士山(2)
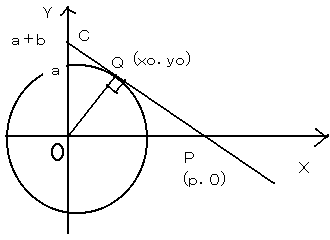
まず、地球の半径をa、富士山の高さをbとし、
地球を半分に切ってxy平面で考えます。
すると、
地球の方程式 x2+y2=a2と、
点C(0,a+b)を通る直線との
交点Q(x0,y0)までが
富士山から見下ろせる範囲となります。

a=6371(km),b=3.776(km)とすれば、Q(219.25,6367.23)
つまり富士山の傾斜を考えなければ、麓から大体219km
(正確には219.294km)の地点まで見渡せることになります。
雲がなければですが。
しかし、TVを使えばどこまででも見ることができます。
この問題をやっていてふと思ったんですけれど、地球の反対側まで穴を空けて、
その穴に落ちた時、加速度はどうなるんでしょうか?
又、中心からずらして穴を空けるとどうでしょう?

NO.265 '99 1/8 Junko 富士山(3)
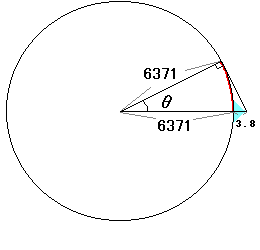
左の図の赤い部分の距離を求めます。
方程式cosθ=6371/(6371+3.776)を解くことにより、角θを求めます。
「mathematica」で解くと、θ=0.0344・・・(ラジアン)となりました。
次に、赤い部分の長さlを求めるために、l=rθの式に代入します。
l=6371×0.0344・・・=219.294・・・となりました。
答えは富士山山頂の真下から半径約219kmの
円内ということになるのでしょうか?

NO.266 '99 1/8 水の流れ 富士山(4)
静岡県の漁師などは富士山の頂上が見えなくなると、だいたい200km
だと、肌で感じていました。
ここで、先ほどの富士山と同じ問題です。
7月末に、私は浜松の中島砂丘に立って、遠く彼方の海をみて、
心を静めていました。
一体何km先の水平線を眺めていたことになるでしょうか。
ただし、私の目の高さを1.5m、地球の半径を6371kmとして、
計算してください。
勿論、地球は球体をして、考えてください。

NO.267 '99 1/8 月の光 連続根号数・その1(1)
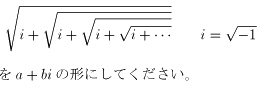

NO.268 '99 1/8 月の光 連続根号数・その2(1)
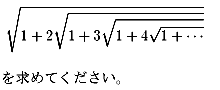

NO.269 '99 1/10 豊作 互いに素(3)


*このTeXファイルもご本人の提供です。

NO.270 '99 1/10 水の流れ 互いに素(4)
自然数N=aαbβcγ・・・(素因数分解した形)とおくと、
Nと互いに素(1以外に公約数をもたない)なものの個数をψ(N)と表す
(オイラー関数)。
ψ(N)=N(1−1/a)(1−1/b)(1−1/c)・・・・・・ となる。
ここで、このオイラー関数の簡単な性質を書きます。
定理1.NとMが互いに素なら、ψ(NM)=ψ(N)・ψ(M)
定理2.N=aαのとき、(aは素数)
ψ(aα)=aα−aα−1=aα(1−1/a)
だから、これと定理1から
ψ(N)=N(1−1/a)(1−1/b)(1−1/c)・・・・・・
定理3.各素因数aに対して、
ψ(1)+ψ(a)+ψ(a2)+・・・+ψ(aα)
=1+(a−1)+(a2−a)+・・・+aα(1−1/a)=aα
例 N=16=24のとき、
ψ(1)+ψ(2)+ψ(4)+ψ(8))+ψ(16)
=1+1+2+4+8
=16
定理4.Nのすべての約数を1,p,q,r,・・・,Nとすると、
ψ(1)+ψ(p)+ψ(q)+ψ(r)+・・・+ψ(N)=N
例 N=15のとき、15とすべての約数は1,3,5,15だから
ψ(1)+ψ(3)+ψ(5)+ψ(15)
=1+2+4+8
=15
そこで、問題です。
ψ(N)=6 となる自然数Nを求めよ。<参考:オイラー関数表参照>
オイラー関数表
| N | ψ(N) | N | ψ(N) | N | ψ(N) | N | ψ(N) | N | ψ(N) |
|---|
| 1 | 1 | 21 | 12 | 41 | 40 | 61 | 60 | 81 | 54 |
| 2 | 1 | 22 | 10 | 42 | 12 | 62 | 30 | 82 | 40 |
| 3 | 2 | 23 | 22 | 43 | 42 | 63 | 36 | 83 | 82 |
| 4 | 2 | 24 | 8 | 44 | 20 | 64 | 32 | 84 | 24 |
| 5 | 4 | 25 | 20 | 45 | 24 | 65 | 48 | 85 | 64 |
| 6 | 2 | 26 | 12 | 46 | 22 | 66 | 20 | 86 | 42 |
| 7 | 6 | 27 | 18 | 47 | 46 | 67 | 66 | 87 | 56 |
| 8 | 4 | 28 | 12 | 48 | 16 | 68 | 32 | 88 | 40 |
| 9 | 6 | 29 | 28 | 49 | 42 | 69 | 44 | 89 | 88 |
| 10 | 4 | 30 | 8 | 50 | 20 | 70 | 24 | 90 | 24 |
| 11 | 10 | 31 | 30 | 51 | 32 | 71 | 70 | 91 | 72 |
| 12 | 4 | 32 | 16 | 52 | 24 | 72 | 24 | 92 | 44 |
| 13 | 12 | 33 | 20 | 53 | 52 | 73 | 72 | 93 | 60 |
| 14 | 6 | 34 | 16 | 54 | 18 | 74 | 36 | 94 | 46 |
| 15 | 8 | 35 | 24 | 55 | 40 | 75 | 40 | 95 | 72 |
| 16 | 8 | 36 | 12 | 56 | 24 | 76 | 36 | 96 | 32 |
| 17 | 16 | 37 | 36 | 57 | 36 | 77 | 60 | 97 | 96 |
| 18 | 6 | 38 | 18 | 58 | 28 | 78 | 24 | 98 | 42 |
| 19 | 18 | 39 | 24 | 59 | 58 | 79 | 78 | 99 | 60 |
| 20 | 8 | 40 | 16 | 60 | 16 | 80 | 32 | 100 | 40 |

NO.271 '99 1/11 Junko 1999年の問題(4)
授業の中で、生徒にも挑戦してもらいました。
(1×9+9)÷9=2
−1+9÷9×√9=2
1+9÷(√9×√9)=2
−1−√9+9−√9=2
1×(9+9)÷9=2
−1+{9÷(9÷√9)}=2
1+9÷√9÷√9=2
1×√9×9÷9=3
1×9÷9×√9=3
1−9÷9+√9=3
1×√9×9÷9=3
1×9−√9−√9=3
1+(9+9)÷9=3
1×9−9+√9=3
1×√9+9−9=3
(1+√9)×9÷9=4
1+√9×√9÷√9=4
1+√9+√9−√9=4
1+√9+9−9=4
1×(9÷9+√9)=4
1+9−9+√9=4
1×9÷9+√9=4
1+9−√9−√9=4
1+√9+9÷9=5
1+9÷9+√9=5
−1+(9+9)÷√9=5
1+√9÷√9+√9=5
1+√9+√9÷√9=5
−1+9−9÷√9=5
(1+9÷9)×√9=6
1×√9×√9−√9=6
1×9÷√9+√9=6
{1+(9÷9)}×√9=6
1×√9+9÷√9=6
−1+9−9÷9=7
−1+9−√9÷√9=7
1+9÷√9+√9=7
1+9−9÷√9=7
1+√9+9÷√9=7
−1+9÷9×9=8
−1+9−9+9=8
−1+9+9−9=8
−1−9+9+9=8
1×9−9÷9=8
−1+√9+√9+√9=8
−1×9÷9+9=8
1×9+9−9=9
1×9−9+9=9
1−9÷9+9=9
1×9×9÷9=9
1×9÷9×9=9
1+9−9÷9=9
1+9−√9÷√9=9
−1+9+9÷9=9
(1+9−9)×9=9
1×9÷9+9=10
(1+9)×9÷9=10
1+9+9−9=10
1−9+9+9=10
1+9−9+9=10
1+9×9÷9=10
1+√9+√9+√9=10
1+9+9÷9=11
1+9÷9+9=11
−1+√9+√9×√9=11
1×√9+√9×√9=12
1×√9×√9+√9=12
1×√(9×9)+√9=12
1×9÷√9+9=12
1×9+9÷√9=12

NO.272 '99 1/11 月の光 定義域(1)

オイラーが解を得ています。

NO.273 '99 1/12 Junko 互いに素(5)
NO.270のオイラー関数表を検証していて、
オイラ−関数の値を求める際には、次の2通りでせめていけばよいということに気づきました。
- N=aα (但し、aは素数)の時、
ψ(N)=aα−aα−1
(NO.270の定理2)
特にN自身が素数の時は、ψ(N)=N−1
例えば、ψ(16)=ψ(24)
=24−23
=16−8
=8
ψ(17)=17−1
=16
- それ以外の時は、N=aαbβcγ・・・(素因数分解した形)として、
aα、bβ、cγ、・・・は互いに素だから、NO.270の定理1より
ψ(N)=ψ(aα)・ψ(bβ)・ψ(cγ)・・・
例えば、ψ(15)=ψ(5×3)
=ψ(5)×ψ(3)
=4×2
=8
「ψ(N)=6 となる自然数Nを求めよ。」を考えてみます。
上記の2つの型別に考えてみます。
- aを素数として、N=aαの時、
ψ(N)=aα−aα−1=aα−1(a−1)=6
- a−1=1とすると、a=2。このとき、2α−1=6よりダメ
- a−1=2とすると、a=3。このとき、3α−1=3よりα=2
従ってN=32=9
- a−1=3とすると、a=4。このとき、4α−1=2よりダメ
- a−1=6とすると、a=7。このとき、7α−1=1よりα=1
従ってN=71=7
- N=aαbβcγ・・・(素因数分解した形)の時、
ψ(N)=ψ(aα)・ψ(bβ)・ψ(cγ)・・・=6
ψ(a)・ψ(b)=2×3=6またはψ(a)・ψ(b)=1×6=6なる組み合わせを探す。
- ψ(N)=3を満たすNは存在しません。
ψ(N)=aα−aα−1=aα−1(a−1)=3
- a−1=1とすると、a=2。
このとき、2α−1=3よりダメ
- a−1=3とすると、a=4。4は素数でないからダメ
- ψ(N)=1を満たすNを探す。
ψ(N)=aα−aα−1=aα−1(a−1)=2
a−1=1とすると、a=2。
このとき、2α−1=1よりα=1
従ってN=21=2
例外的に、ψ(1)=1。しかし1では話が進展しない。
ψ(N)=6を満たすのは、前段の話しよりN=7とN=9だから、
ψ(14)=ψ(2)×ψ(7)=1×6=6
ψ(18)=ψ(2)×ψ(9)=1×6=6
蛇足ながら、ψ(28)=ψ(2)×ψ(14)=1×6=6とはなりません。
以上により、ψ(N)=6を満たす自然数Nは、
N=7,9,14,18の4つに限る。
さて、オイラ−関数表を見ていて思ったのですが、
「N≧3に対して、ψ(N)は必ず偶数となる」ようですね。

 E-mail
E-mail
 戻る
戻る
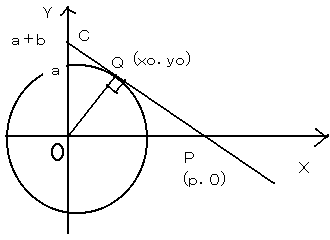



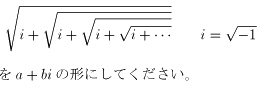
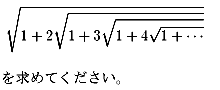



 E-mail
E-mail
 戻る
戻る