Weekend Mathematics／コロキウム室／1999.1〜3／NO.41

コロキウム室



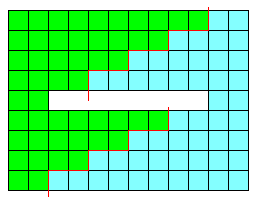
NO.335　　　　'99 2/15 　　 Junko 　　　 ナプキンの問題（２）
　　

左の図のように切り離して、右の図のように組み合わせればいいのではないでしょうか。



NO.336　　　　'99 2/15 　　 水の流れ 　　　 ゼーター関数物語（１）
　　

「数学の知性」Ｗ．ダンハム著：中村由子訳（現代数学社） 読んで、これからゼター関数ζ（２）物語を投稿します。

「時は、１７世紀後半ヨーロッパ大陸のフランスのパリにドイツの外交官 として、派遣されていたライプニッツ（１６４６〜１７１６）がいました。
幸運なことに、当時ドイツの科学者ホイエンス（１６２９〜１６９５）は パリに在住していました。このホイエンスに数学の勉強を教わっていました。
さて、このときの問題です。
みなさんは三角数をご存じですか？１，３，６，１０，・・・ と三角形になるように配置したときの数字です。
では、その三角数の逆数の和を求めてください。
すなわち、Ｓ＝１＋１／３＋１／６＋１／１０＋・・・・ のＳの値を求めてください。」

＜注：　実は、この解法がライプニッツのパリ在住４年間（１６７２〜１６７６） の数学的洞察力を開花させるきっかけとなったものです。＞



NO.337　　　　'99 2/15 　　 Junko 　　　 三角形の面積（２）
　　

オ−ソドックスな解法を３つ






NO.338　　　　'99 2/16 　　 みや　　 　　　 ゼーター関数物語（２）
　　






NO.339　　　　'99 2/16 　　 水の流れ 　　　 ゼーター関数物語（３）
　　

ゼター関数ζ（２）物語を第２夜を送ります。
「１７世紀後半、１６８４年、ライプニッツは学術誌 「Ａｃｔａ　Ｅｒｕｄｉｔｏｒｕｍ］に 素晴らしき微分学を発表しました。
ライプニッツは１７１６年亡くなりましたが、 この後継者である二人のスイス人の兄弟はヨーロッパ中に微分を広め、 定着させる大きな力になりました。
兄ヤコブ・ベルヌーイ（１６５４〜１７０５）は確率論で知られています。
弟ヨハン・ベルヌーイ（１６６７〜１７４８）は兄ヤコブが１６８９年 発表した「無限級数に関する論文」の中に ”調和級数は無限大に発散する”ことを証明しています。
ここで、問題です。

調和級数　１＋１／２＋１／３＋１／４＋１／５＋・・・・・は無限大に発散する。

皆さんは、これを現代風にでも結構ですので、証明してください。
後で、ヤコブ著「ｔｒａｃｔａｔｕｓ」（１７１３年） の中での発散の証明を書きます。今日はここまです。




NO.340　　　　'99 2/17 　　 Junko 　　　 1999!の桁数（５）
　　

１９９９年数学オリンピック予選問題の７番の問題です。



Ｃopyrightｩ 1999 by Mathematical Olympiad Foundation of Japan.
著作権は数学オリンピック財団に帰属します.



NO.341　　　　'99 2/17 　　 Junko 　　　 複素数（２）
　　

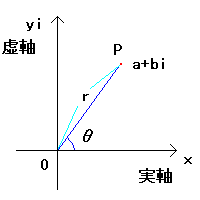
複素数 z=a+bi (a,bは実数、iは虚数単位)は２次元の数と考えることができます。







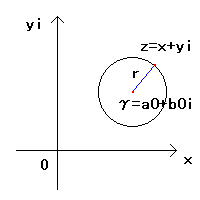
NO.342　　　　'99 2/18 　　 Junko 　　　 複素数（３）
　　

一般にｎ次元の複素数を考えることはできるでしょうか？

「複素数への招待」(宮西正宜・増田佳代著、日本評論社)に次のような 記述があります。

Ｅ1、Ｅ2、・・・、Ｅn-1、 を数を表す単位として
Ｚ＝ａ0＋ａ1Ｅ1＋ａ2Ｅ2＋・・・＋ａn-1Ｅn-1 とすればいいわけです。
和差はいいとして、積を定義するには、 ＥiＥjをどう定義するかが問題です。
さらに割り算を定義するためには、共役数Ｚ'をどう定義するかが問題になります。
四則演算をすべて定義できるのは、n=1,3,7に限られるとあります。

n=1の場合はいわゆる複素数です。

n=3の場合の例として、ハミルトンの四元数があげられています。
数を表す単位として、i、j、kを用いて、 Ｚ＝a+bi+cj+dk(a,b,c,dは実数)なる数を考えます。
積は、i2=j2=k2=-1、ij=-ji=k、jk=-kj=i、 ki=-ik=jで定義します。
定義からわかるように、可環ではありません。
Ｚ＝a+bi+cj+dkに対する共役数Ｚ’＝a-bi-cj-dkで与えます。
絶対値｜Ｚ｜＝ＺＺ’＝a2+b2+c2+d2となります。

n=7の場合の例とは、ケ−レ−の８元数です。
Ｚ＝a0+a1i1+a2i2+a3i3+ a4i4+a5i5+a6i6+a7i7
(a0,a1･･･a7は実数)という形になります。




NO.343　　　　'99 2/18 　　 Junko 　　　 ゼーター関数物語（４）
　　






NO.344　　　　'99 2/19 　　 水の流れ 　　　 ゼーター関数物語（５）
　　

「ゼター関数ζ（２）物語第３夜の始まり、始まり。
見事に、調和数列　１＋１／２＋１／３＋１／４＋１／５＋・・・ が無限大に発散する証明が終わりました。
ところが、弟ヨハン・ベルヌーイは兄ヤコブ著「tractatus」の中で、 ライプニッツの収束する級数
１／２＋１／６＋１／１２＋１／２０＋・・・＝１
を利用して、こんな風に書いています。

＜証明＞　最初の項を省いて、調和数列を
Ａ＝１／２＋１／３＋１／４＋１／５＋・・・　　とおく。
さらに、後に参照するために、分子が１，２，３，４，・・・ となるよう変換しておきます。
すると、 Ａ＝１／２＋２／６＋３／１２＋４／２０＋５／３０＋・・・
ライプニッツの収束する級数をＣとおき、それから順次
１／２、１／６、１／１２、１／２０、・・・ を省きながら一連の級数を作ります。

Ｃ＝１／２＋１／６＋１／１２＋１／２０＋１／３０＋・・・＝１
Ｄ＝１／６＋１／１２＋１／２０＋１／３０＋・・・＝Ｃ−１／２＝１／２
Ｅ＝１／１２＋１／２０＋１／３０＋・・・＝Ｄ−１／６＝１／２−１／６＝１／３
Ｆ＝１／２０＋１／３０＋・・・＝Ｅ−１／１２＝１／３−１／１２＝１／４
Ｇ＝１／３０＋・・・＝Ｆ−１／２０＝１／４−１／２０＝１／５
・・・

ここで、ヨハンは上の整然と並んだ式の式を左から順に縦に足してみます。
すると 

Ｃ＋Ｄ＋Ｅ＋Ｆ＋Ｇ＋・・・

＝１／２＋（１／６＋１／６）＋（１／１２＋１／１２＋１／１２）＋　（１／２０＋１／２０＋１／２０＋１／２０）＋・・・
＝１／２＋２／６＋３／１２＋４／２０＋・・・
＝Ａ
皆さん、何か気がつきましたか。 先にあげた式とまったく同じものになっています。 
Ｃ＋Ｄ＋Ｅ＋Ｆ＋Ｇ＋・・・＝１＋１／２＋１／３＋１／４＋１／５＋・・・
　　　　　　　　　　　　　＝１＋Ａ
であることがわかります。
したがって、もう読者の皆さんはお分かりでしょう。
ヨハンは　１＋Ａ＝Ａ　であると結論しています。
彼自身それを”全体が部分に等しい”と書いています。
これは、それ自身より１大きい数に等しい有限な数などありませんから、 １＋Ａは無限の数量であるということです。 彼の論証はこれで完了します。
先のjunkoさんの証明方法に照らしても実にユニークな方法です。
さて、この調和級数の発散になる証明はヨハンが最初ではありません。 それよりの早く、少なくとも二人の数学者がこの発散の証明をしています。 もっとも早かったのは１４世紀のフランスの数学者ニコル・オレスム （１３２３〜１３８２）でした。 彼の証明は調和数列の本質に迫るもので、 とても信じられない素晴らしい証明です。
そこで、彼が証明した問題です。 ただ、今風にアレンジしました。
『任意の整数をｋとして、
　１＋１／２＋１／３＋１／４＋・・・＋１／２ｋ＞（ｋ＋１）／２』
皆さん、ニコル・オレスムと同じ証明になるでしょうか？ もし、そうなら数学的真理の普遍性を実感します。
果たして、どうでしょうか。これで、第３夜は終わります。 ああー、睡魔が現れて、眠むくなりました。お休みなさい。」



NO.344　　　　'99 2/19 　　 水の流れ 　　　 三角形の面積（２）
　　



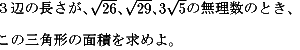
＜解答＞
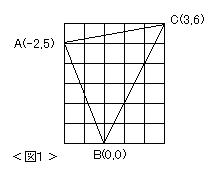２９＝５２＋２２
２６＝５２＋１２
４５＝６２＋３２

に着目して、座標平面上に、 点Ａ（−２，５），点Ｂ（０，０），点Ｃ（３，６） のように３頂点を格子点上に取ります。

図のように２辺が５と６の長方形の面積から、 ３つの三角形の面積を引いてみると、
△ＡＢＣ＝６×５−（２×５＋５×１＋３×６）÷２＝３０−３３／２＝２７／２（答）

＜解説＞
この問題を作問した意図は、３辺の長さが無理数でも、 答えの面積は有理数（分母は２） になる不思議さを知ってもらい、なぜだろうと疑問を抱せたかったのです。
さらには、この三角形を座標平面上で書くと、 ３頂点がすべて、格子点になるように取れて、 後は小学生にでも解けるようになります。
　勿論、他の解法は一杯あって、 別解を見つけるには楽しくなるはずです。
そして、とっておきは、今から述べるピックの定理です。 １８９９年、オーストリヤの数学者Ｇ．Ｐｉｃｋ によって、 発見された定理を使うと、鮮やかに解けます。

尚、この定理の証明は、岐阜県の研究会で同席した各務原市内にある 高校の先生から頂いたノートを参考にして、書いてあります。 （この先生も今では、原本がどこからか忘れられたとのことです）

「Ｐｉｃｋの定理」：平面上の格子多角形Ｍにおいて、 辺上にある格子点の個数をｂ
Ｍの内部にある格子点の数をｃとすると、その面積Ｓ(Ｍ) は次の式で表される。
Ｓ(Ｍ)＝（ｃ−１）＋ｂ／２
次の３つの命題から、順に分けて証明していきます。
命題１：（頂点のみが格子点である三角形の場合）
内部にも辺上にも格子点がなく、頂点のみが格子点である三角形▲（以下基本
三角形と呼ぶ）の面積は１／２である。 すなわち、Ｓ(▲)＝１／２・・・@


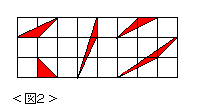図２のような、基本三角形の面積はすべて１／２である。
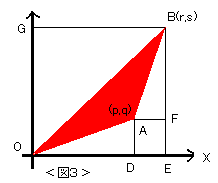次に、図３のように座標平面上で、点Ａ（ｐ，ｑ）と取り、線分ＯＡを正の向きに 回転して，線分ＯＢになるように、点Ｂ（ｒ，ｓ）を取る。
このとき、３点Ｏ，Ａ，Ｂでできる三角形の面積Ｓ（△ＯＡＢ）は よく知られているように 、Ｓ（△ＯＡＢ）＝（ｐｓ−ｑｒ）／２ ・・・Aである。
そこで、△ＯＡＢが基本三角形であるとき、ｐｓ−ｑｒ＝１であることを以下に示す。
多角形Ｍの内部（辺上は含まない）にある格子点の数をＬ（Ｍ）と書く。
△ＯＡＢを含む最小の長方形ＯＥＢＧを書く。長方形ＯＥＢＧに含まれる格子点は全部
で（ｒ＋１）（ｓ＋１）個であるが、そのうち辺ＯＥ，ＥＢ，ＢＧ，ＧＯ上にあるのは
全部で、２（ｒ＋１）＋２（ｓ＋１）−４＝２（ｒ＋ｓ）個である。
よって、Ｌ（□ＯＥＢＧ）＝ （ｒ＋１）（ｓ＋１）−２（ｒ＋ｓ）
　　　　　　　　　　　　　　　　＝（ｒ−１）（ｓ−１）
したがって、Ｌ（△ＯＢＥ）＝Ｌ（□ＯＥＢＧ）／２＝（ｒ−１）（ｓ−１）／２
同様に，Ｌ（△ＯＡＤ）＝（ｐ−１）（ｑ−１）／２
Ｌ（△ＡＢＦ）＝（ｒ−ｐ−１）（ｓ−ｑ−１）／２
Ｌ（□ＡＤＥＦ）＝（ｒ−ｐ−１）（ｑ−１）
図３から分かるように、
Ｌ（△ＯＢＥ）＝Ｌ（△ＯＡＢ）＋Ｌ（△ＯＡＤ）＋ Ｌ（△ＡＢＦ）＋Ｌ（□ＡＤＥＦ） ＋Ｌ（ＯＡ）＋Ｌ（ＡＢ）＋Ｌ（ＡＤ）＋Ｌ（ＡＦ）＋１
最後の＋１は点Ａのことである。
△ＯＡＢが基本三角形より、Ｌ（△ＯＡＢ）＝Ｌ（ＯＡ）＝ Ｌ（ＡＢ）＝０であるから
（ｒ−１）（ｓ−１）／２
　　　　　　＝（ｐ−１）（ｑ−１）／２ ＋（ｒ−ｐ−１）（ｓ−ｑ−１）／２
　　　　　　　＋（ｒ−ｐ−１）（ｑ−１）＋（ｑ−１）＋（ｒ−ｐ−１）＋１

これを計算して、ｐｓ−ｑｒ＝１ ・・・B
これで、命題１のＳ(▲)＝１／２が証明された。

命題２：格子多角形は基本三角形に分割できる。

＜解説＞ その方法は、まず格子多角形を格子三角形に分割し、格子三角形を基本三角形に分割
すればよい。基本三角形への分割の手続きは次のようになる。
例えば、＜図４＞をみます。


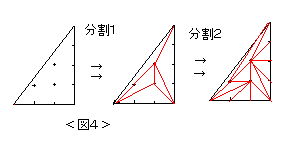（分割１） 格子三角形の内部にある１つの格子点と３つの頂点を結んで三角形を３つに分割する。
（分割２） 三角形の内部に格子点がないときは、辺上の格子点と反対側の頂点とを結ぶ。
（分割操作１）を繰り返すことによって、内部に格子点を含まない三角形にまで分割でき、
　　　さらに，
（分割操作２）を繰り返せば基本三角形にまで分割できる。


命題３：格子多角形Ｍを基本三角形に分割したとき、
三角形の数は２ｃ＋ｂ−２ である。
ただし、ｃはＭの内部にある格子点の数、ｂは辺上にある格子点の数である。


＜証明＞ 多面体におけるオイラーの定理を使って、証明します。
基本三角形に分割したときの頂点の数をｄとすると、
ｄ＝ｃ＋ｂ・・・・・・C
辺の数をｅ，面の数（三角形の数）をｆとすると
　　　　ｅ＝ｅ’＋ｅ” ここで、ｅ’はＭの内部の辺の数、ｅ”はＭの辺上の辺の数である。

＜図４＞の例では、ｅ’＝１４，ｅ”＝８ である。
ところで、ｅ”＝ｂ、また１つの三角形の辺の数は３つであるから、
３ｆ＝２ｅ’＋ｅ”
したがって、３ｆ＝２（ｅ−ｅ”）＋ｅ”＝２（ｅ−ｂ）＋ｂ
ゆえに、 ｅ＝（３ｆ＋ｂ）／２・・・D
そして、C、Dをオイラーの公式 ｄ−ｅ＋ｆ＝１ へ代入して
ｃ＋ｂ−（３ｆ＋ｂ）／２ ＋ｆ＝１
ゆえに、ｆ＝２ｃ＋ｂ−２ で命題３の証明終わり。

以上の命題１，命題２，命題３から、
Ｓ（Ｍ）＝（２ｃ＋ｂ−２）／２ ＝（ｃ−１）＋ｂ／２
となり、Ｐｉｃｋの公式が証明できた。

最後に、問題に適用します。＜図１＞をみて、
内部にある格子点の数ｃと辺上にある格子点の数ｂを数えると、
ｃ＝１２、ｂ＝５ だから、
求める面積はピックの公式より、
（１２−１）＋５／２＝２７／２・・・（答）








E-mail 戻る