Weekend Mathematics／コロキウム室／1999.1〜3／NO.48

コロキウム室



NO.402　　　　'99 3/14 　　 月の光 　　　 定義域（８）
　　

NO.272を書き直します。


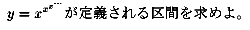
つまり、あるｘに対してｙの値が存在し、一つに定まる区間と考えて下さい。
例えば、ｘ＝０だったらｙは０と１二つの値になるので０は入らない。
ｘ＝−２は途中で虚数になるのでこれも入らない。
ｘ＝√２だとｙ＝２になるので問題の区間内にある。ということです。



NO.403　　　　'99 3/14 　　 水の流れ 　　　 ゼーター関数物語（３７）
　　

ゼーター関数ζ（２）物語第１０夜の始まりです。
さて、昨夜次のような問題を出したところ、 「月の光」さんや「Junko」によって、 それぞれ、エレガントでかつユニークな解法で値を求められました。



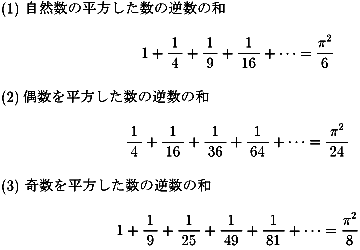
皆さんも、これらの値を覚えておかれるといいでしょう。

レオンハルト・オイラーはこれでもう十分に満足してこの素晴らしい栄光の上に どっかりとあぐらをかいていませんでした。 価値あることなら何事も徹底的に掘り下げていくという才能が彼の数学の特徴です。 かの素晴らしい“和”の場合も、彼にしてみればまだ表面を引っ掻いただけに過ぎませんでした。 オイラーは自らがキ−となる式をもう一度思い出してください。



オイラーは偶然にも、イギリス人のジョン・ウｫリス（１６１６〜１７０３）に よって発見されたπの近似式と同じ結果を 彼独自のユニークな方法で得ています。

それでは、今夜の問題です。
ジョン・ウｫリスの公式をオイラー風に求めてください。
次の夜に、ζ（４）、ζ（６）、ζ（８）を求めますが、予習をお願いします。

一般に、対称式は基本対称式の整式として表されます。

問題

  1. ｓ１＝ａ＋ｂ，ｓ２＝ａｂ　とおくとき、
    ａ２＋ｂ２　をｓ１，ｓ２で表してください。
  2. ｓ１＝ａ＋ｂ＋ｃ，ｓ２＝ａｂ＋ａｃ＋ｂｃ，ｓ３＝ａｂｃ　とおくとき、
    ａ３＋ｂ３＋ｃ３　をｓ１，ｓ２，ｓ３で表してください。　
  3. ｓ１＝ａ＋ｂ＋ｃ＋ｄ，ｓ２＝ａｂ＋ａｃ＋ａｄ＋ｂｃ＋ｂｄ＋ｃｄ，
    ｓ３＝ａｂｃ＋ａｂｄ＋ａｃｄ＋ｂｃｄ，ｓ４＝ａｂｃｄ　とおくとき、
    ａ４＋ｂ４＋ｃ４＋ｄ４を ｓ１，ｓ２，ｓ３，ｓ４で表してください。
今夜はこれで終わりです。お休み！　　　



NO.404　　　　'99 3/14 　　 Junko 　　　 素数の逆数の総和（３）
　　

素数が無限に存在することの、オ−ソドックスな証明です。
背理法によります。

もし素数の数が有限個だとして、それを小さい順に ｐ１、ｐ２、ｐ３、・・・、ｐｍとします。
新たに、(ｐ１・ｐ２・ｐ３・・・ｐｍ＋１)なる数を考えます。
この数は、任意の素数ｐｎで割れませんので、素数です。 しかも、最大の素数であるｐｍよりも大きい数であり、 これは明らかに矛盾です。




NO.405　　　　'99 3/14 　　 Junko 　　　 素数の逆数の総和（４）
　　

大学時代のゼミで読んだ「An Introduction to the Theory of Numbers」の中に、 素数の逆数の和が発散する事の証明がありますので、紹介します。

素数を小さい方から順に、 ｐ１、ｐ２、ｐ３、とします。


このことから逆に素数が無限に存在することが言えると思います。 もし素数が有限個しかなかったら、上の級数が発散するはずはないからです。



NO.406　　　　'99 3/14 　　 豊作 　　　 定義域（９）
　　

NO.272の問題はつまり



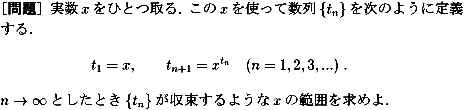
という問題であるという解釈でよろしいでしょうか？



NO.407　　　　'99 3/16 　　 Junko 　　　 ゼーター関数物語（３８）
　　

NO.403の宿題の答えです。 

  1. ａ２＋ｂ２＝(ａ＋ｂ)２−２ａｂ＝ｓ１２−２ｓ２

  2. 展開公式
(ａ＋ｂ＋ｃ)２＝ａ２＋ｂ２＋ｃ２＋２ａｂ＋２ｂｃ＋２ｃａ

(ａ＋ｂ＋ｃ)(ａ２＋ｂ２＋ｃ２−ａｂ−ｂｃ−ｃａ)＝ａ３＋ｂ３＋ｃ３−３ａｂｃを使って、

ａ３＋ｂ３＋ｃ３＝ｓ１３−３ｓ１ｓ２＋３ｓ３

  3. ａ４＋ｂ４＋ｃ４＋ｄ４＝ｓ１４−４ｓ１２ｓ２＋２ｓ２２＋４ｓ１ｓ３−４ｓ４
これは、「ｓ１４−(ａ４＋ｂ４＋ｃ４＋ｄ４)」 を展開し、残った項を見ながら見当をつけて探していきました。
実際の計算は「mathematica」に手伝ってもらいました。



NO.408　　　　'99 3/16 　　 Junko 　　　 ゴルフのスコア （２）
　　

  1. 重複順列　３３＝２７
  2. 重複組み合わせ　３Ｈ３＝５Ｃ３＝１０
  3. (2)の１０通りについて今度は順番も考慮して(つまり２７通りについて)考えます。
    パ−(P)、ボギ−(B)、ダブルボギ−(D)とします。


かろうじて１００をきっています。 このくらいのスコアで回ってみたいものです。 一生かかっても無理だろうなあ・・・。



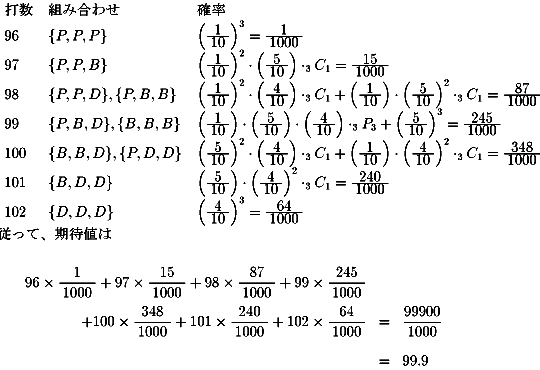
NO.409　　　　'99 3/17 　　 水の流れ 　　　 ゼーター関数物語（３９）
　　

ａ４＋ｂ４＋ｃ４＋ｄ４は ４次の同次式ですから、基本対称式の整式に表されることより、与式は次のようになります。
ｓ１は１次式、ｓ２は２次式、 ｓ３は３次式、ｓ４は４次式に注目していくと、
与式＝ｓ１４＋Ａｓ１２ｓ２＋Ｂｓ２２＋Ｃｓ１ｓ３＋Ｄｓ４ と表されます。
ここで、両辺のａ，ｂ，ｃ，ｄに４組の意味のある数値を代入して、 Ａ，Ｂ，Ｃ，Ｄの４元方程式を作って、解きます。
ちなみに、（ａ，ｂ，ｃ，ｄ）＝（１，１，０，０）、（１，１，１，０）、（１， １，１，１）、 （１，−１，１，−１）を代入して、
２＝１６＋４Ａ＋Ｂ
３＝８１＋２７Ａ＋９Ｂ＋３Ｃ
４＝２５６＋９６Ａ＋３６Ｂ＋１６Ｃ＋Ｄ
４＝４Ｂ＋Ｄ
これを解いて、正解に至ります。



NO.410　　　　'99 3/17 　　 水の流れ 　　　 ゼーター関数物語（４０）
　　

(一部記述にあやまりがありました。ごめんなさい。訂正junko3/18)

ゼーター関数ζ（２）物語第１１夜の始まり、始まり。
昨夜の予習問題は、次のように基本対称式で表されます。 NO.407をご覧ください。

  1. ａ２＋ｂ２＝(ａ＋ｂ)２−２ａｂ＝ｓ１２−２ｓ２
  2. ａ３＋ｂ３＋ｃ３＝ｓ１３−３ｓ１ｓ２＋３ｓ３
  3. ａ４＋ｂ４＋ｃ４＋ｄ４＝ｓ１４−４ｓ１２ｓ２＋２ｓ２２＋４ｓ１ｓ３−４ｓ４

そこで、オイラーの自らが発見したキ−となる式をもう一度思い出してください。


したがって、今夜の宿題です。
これを利用して、ζ（２）、ζ（４）、ζ（６）、ζ（８）まで、求めてください。
この続きは明日の夜お話しましょう。 オイラーはパソコンのない時代にζ（２６）までよく手ですごい計算をしたものだと驚きます。







E-mail 戻る