Weekend Mathematics/コロキウム室/1999.1~3/NO.36
コロキウム室
NO.285 '99 1/16 Junko 星形n角形(2)
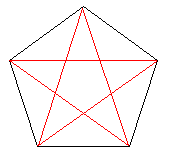 試しに正5角形から順にかいてみました。
試しに正5角形から順にかいてみました。
正n角形の中にできる星形n角形の個数をf(n)で表す
とします。
f(5)=1となります。
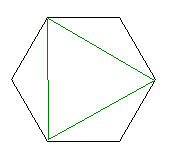 正6角形については、できません。
正6角形については、できません。
f(6)=0となります。
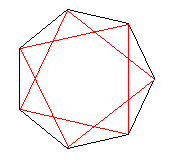
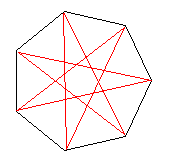 正7角形については、2種類できます。
正7角形については、2種類できます。
時計まわりに、2つおきに頂点をとっていくものと、
3つおきにとっていくものです。
従って、f(7)=2となります。
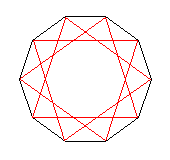 正10角形については、3つおきに頂点をとっていくことでできるものだけです。
正10角形については、3つおきに頂点をとっていくことでできるものだけです。
f(10)=1
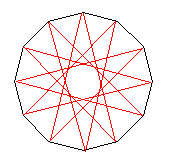 正12角形については、5つおきに頂点をとっていくことでできるものだけです。
正12角形については、5つおきに頂点をとっていくことでできるものだけです。
f(12)=1
一般にf(n)はどうなるか? というと、
オイラ-関数ψ(n)を使って、
f(n)=(1/2)・ψ(n)-1となります。
オイラ-関数ψ(n)というのは、n以下の自然数のうち、
nと互いに素なものの個数です。
正n角形の任意の頂点から、m個おきに対角線をひくとします。
m=1とm=n-1は除外します。
なぜなら、対角線とはならないからです。
nとmが互いに素でないとき、すなわち1以外の公約数を持つときは、
全ての頂点を回る前に、スタ-ト地点に戻ってきてしまうことになるのでだめです。
(正6角形の時のように・・・)
m=kの場合と、m=n-kの場合は結果として同じ図形ができます。
星形を逆にたどることになるからです。
従って以上のことをまとめると、
f(n)=(1/2)・{ψ(n)-2}
=(1/2)・ψ(n)-1 となります。

NO.286 '99 1/16 Junko 富士山(5)
NO.265で、富士山の高さを3.776としたところを、
身長の0.0015として同じように計算します。
方程式cosθ=6371/(6371+0.0015)を解くことにより、角θを求めると、
θ=0.000686・・・(ラジアン)となりました。
l=rθの式に代入すると、
l=6371×0.000686・・・=4.371・・・となりました。
答えは約4.3kmということになるのでしょうか?

NO.287 '99 1/17 水の流れ 分数の問題・その後(8)
NO.281について、
<解答1>はこれは数学的にいわゆる演繹法という
解答方法です。
<解答2>はこれは数学的にいわゆる帰納法という
解答方法です。1つでも反例があればそれは命題
として「偽」ですから、この証明も可です。
だから、優劣はつけられません。
したがって、いずれも「正しい」のです。

NO.288 '99 1/17 Junko 四角形の最大値 (2)
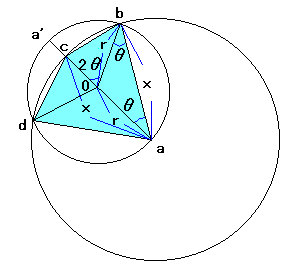
左の図のように、三角形oabは二等辺三角形となります。
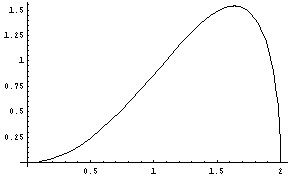
ac=x、∠aob=2θより、求める四角形の面積は、
S(x)=2・(1/2)・x・r・sin2θ
=xrsin2θ
=2xrsinθcosθ

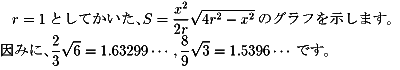
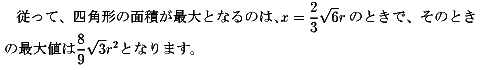

NO.289 '99 1/18 ヴァー 互いに素(6)
No.260の月の光さんの互いに素の問題を図にしてみました。
横方向のxとして1から100までの自然数を、
縦方向のyとして1から100までの自然数をならべて、
その交点(x,y)について、xとyが互いに素のときには黒、
そうでないときには白という風に色を付けました。
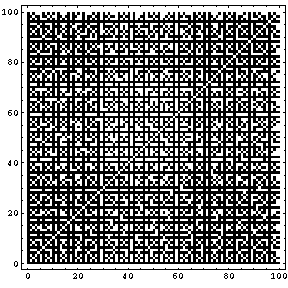
この場合は、黒の割合が6087/10000になりました。(1/20 訂正、白黒逆でした。)

NO.290 '99 1/18 Junko 連続自然数の和(1)
1/16に行われたセンタ-試験<数学Ⅱ・B>に
次のような問題が出題されています。
整数15はつぎのように連続した正の整数の和として表すことができる。
15=1+2+3+4+5=4+5+6=7+8
1より大きい整数nについて、これを連続した2つ以上の正の整数の和で
表すことができるかどうかを調べるプログラムを作った。
途中省略
(3)2から9までの数をnとして、このプログラムを実行する。
このとき、Yesが1回も表示されないnを小さい順に書くと、□、□、□である。
Yesが1回も表示されないというのは、
連続した2つ以上の正の整数の和で表すことができないということを意味します。
答えは2,4,8です。
「連続自然数の和として表すことができない数は、
2mという形をしたものに限る」
ように思います。
試しに16,32,64と調べてみると、確かにそうなっています。
そしてそれ以外のものは、
連続した正の整数の和として表すことができるようです。
なぜなのでしょう?

NO.291 '99 1/18 水の流れ 等分点
ある長さの線分ABについて、2等分点に2,3等分点に3の
文字を書き入れていきます。
4等分点、5等分点、・・・、についても同様にしていきます。
もちろん、既に記入してある場合もあります。
そこで、2000等分点を書き入れたとき、新たに増えた
点はいくつありますか。

NO.292 '99 1/18 水の流れ 格子点
xy平面上の1≦x≦20、1≦y≦20の部分にある400個
の格子点(x座標も、y座標も整数である点)を考えます。
これらの点と原点Oを結ぶ線分のうち、端点以外に格子点が
存在しないものものは何本ありますか。

NO.293 '99 1/19 Junko 分数の問題・その後(9)
12月に出題した分数の問題についてです。
「Idaho Poteto」さんのおっしゃるように
単位分数の和による表現を「少なくとも1通り」示していただければ、
正解と考えて出題しました。
(それ以上のことも内心期待はしていましたが・・・。)
「マサボー」さんは、私が出題した問題としてではなく、
もっと広い意味で「任意の分数(有理数)を単位分数の和として表すこと」
と考えているのではないでしょうか。
かつて、フェルマは
「22n+1という数はn=0,1,2,・・・に対して
素数を与える」と考えました。
これらの数はフェルマ数と呼ばれ、Fnと表されます。
F0=21+1=3
F1=22+1=5
F2=24+1=17
F3=28+1=257
F4=216+1=65537
でいずれも素数です。
しかしながら後にオイラ-が、F5が合成数であることを見つけました。
F5=232+1=4294967297=641×6700417です。
おそらくフェルマは上記の命題を証明しようと試みたのでしょうが、
反例を1つでも見つけてしまえばそれでおしまいです。
NO.281については、
どちらももちろん正しいわけです。
天才(?)は別として、
いきなり「解答1」のような答え方をするのはむずかしいと思います。
やはり最初は「解答2」のように具体的に考えてみるのがいいと思うし、
生徒に説明するような場面では納得もしてもらえると思います。
「解答1」の方がかっこいいという雰囲気があるような気もしますが、
これが数学嫌いを生んでいるような気もします。
問題に取り組む時も、具体的なモデルをたくさん知っていた方が、
その問題の理解に役立つと思います。
ただし命題を覆すなら反例1つで充分ですが、
命題を証明する時は具体例をたくさん示してもだめなのはもちろんです。

NO.294 '99 1/19 水の流れ 互いに素(7)
NO.289で、「ヴァ-」
さんが100までについて図示してくださいました。
これを、オイラ-関数表で計算すると、確かに
2{ψ(2)+ψ(3)+・・・ψ(100)}+1=2×3043+1=6087となっています。
「豊作」さんのレポ-トによれば、
10000×(6/π2)=6079.27・・・ですのでまあまあいい感じですね。

 E-mail
E-mail
 戻る
戻る
 試しに正5角形から順にかいてみました。
試しに正5角形から順にかいてみました。 正6角形については、できません。
正6角形については、できません。
 正7角形については、2種類できます。
正7角形については、2種類できます。 正10角形については、3つおきに頂点をとっていくことでできるものだけです。
正10角形については、3つおきに頂点をとっていくことでできるものだけです。 正12角形については、5つおきに頂点をとっていくことでできるものだけです。
正12角形については、5つおきに頂点をとっていくことでできるものだけです。



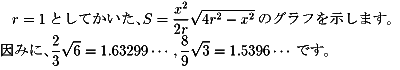
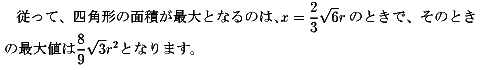

 E-mail
E-mail
 戻る
戻る