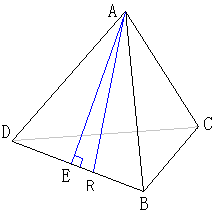
 (1)DBの中点をEとする。
この正四面体の1辺の長さが6であることから、DB=3
(1)DBの中点をEとする。
この正四面体の1辺の長さが6であることから、DB=3AE2=AD2−DE2=36−9=27
AR2=AE2+ER2=27+1=28
AR=√28=2√7
Weekend Mathematics/コロキウム室/1999.1〜3/NO.46
NO.381 '99 3/4 Junko 正四面体の問題(4)
NO.362の解答です。
 (1)DBの中点をEとする。
この正四面体の1辺の長さが6であることから、DB=3
(1)DBの中点をEとする。
この正四面体の1辺の長さが6であることから、DB=3
AE2=AD2−DE2=36−9=27
AR2=AE2+ER2=27+1=28
AR=√28=2√7
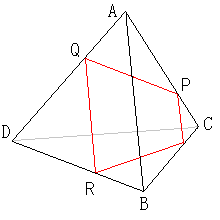
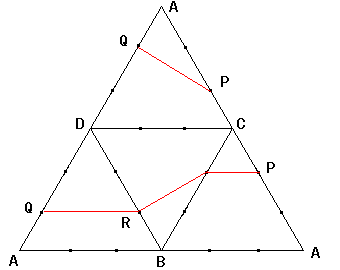
(2)については次の図のようになります。

NO.382 '99 3/4 Weadore 宇宙空間での最短経路問題(4)
NO.353
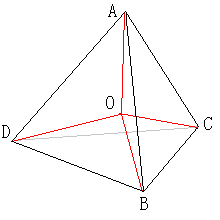
の正四面体のネットワークが最短であることを示す。
まず、正四面体ABCDの内部にある点Oをつないでできる。
AO+BO+CO+DOの最短のネットワークについて議論をする。
AB,CDと平行でO点を通る平面と、ABの中点とCDの中点
を結んでできる線分との交点をO'とする。
ここで、点Aの上記で定義した平面と対象な点をA'とすると、
A'とBを結んだ線分とその平面との交点がO'になる。
よって、AO + BO = A'O + BO≧A'O' + BO' =AO' + BO'
∴AO + BO ≧ AO' + BO'
同様に、CO + DO ≧ CO' + DO'
よって、OはABとCDとの中点同士を結んだ線分上
に存在する。また同様に、ADとBCの中点同士を結んだ
線分上にも存在することになる。
よって、この条件を満たす点Oは正四面体ABCDを内接する
球の中心となります。
また、正四面体の内部に2点、点が存在したときは、
ネットワークの重みが明らかに釣り合わない。
また、三点以上存在しても、今度は閉じた回路を持ってしまう。
よって、[No.353]でできたネットワークが最短であることが示された。
次回は、本題である正六面体について議論をします。お楽しみに。

NO.383 '99 3/5 水の流れ 素数の逆数の総和 (2)
問題1「素数は無限に存在するか」
<証明>コロキウム室のNO.373
で証明されたように調和級数が+無限大に発散します。
もし、素数が有限個しかなければ、右辺のΠ1/(1−1/p)は有限の値になり、
+無限大に発散することに反します。よって、素数は無限に存在します。
問題2「素数の逆数の総和は+無限大に発散する」
<証明>コロキウム室のNO.377
で証明された(1)を使います。
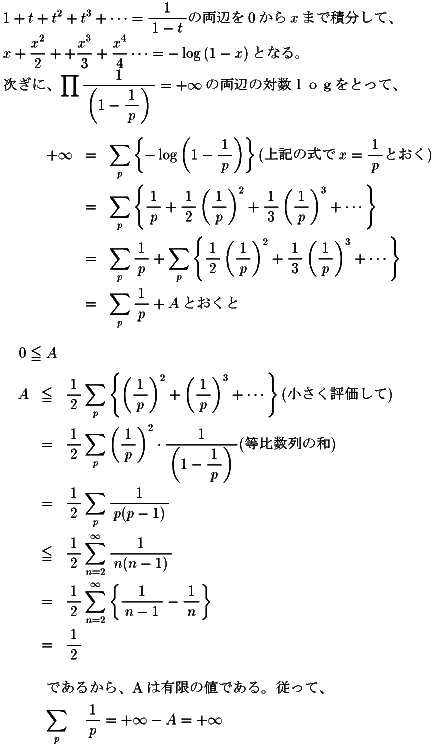
すなわち、素数の逆数の和は+無限大に発散する。
<この証明は過去の「大学への数学」に載っていました>

NO.384 '99 3/5 月の光 ゼーター関数物語(27)
NO.379の
『次の条件を満たすn次の多項式P(x)を見つけなさい。
P(0)=1、P(a1)=0,P(a2)=0,
P(a3)=0,・・・,P(an)=0』に対する答えです。
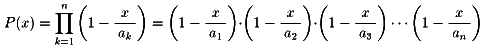

NO.385 '99 3/6 月の光 ゼーター関数物語(28)
NO.357の(2)についてです。


NO.386 '99 3/6 月の光 不思議な級数(1)
(一部記述にあやまりがありました。ごめんなさい。訂正junko3/23)
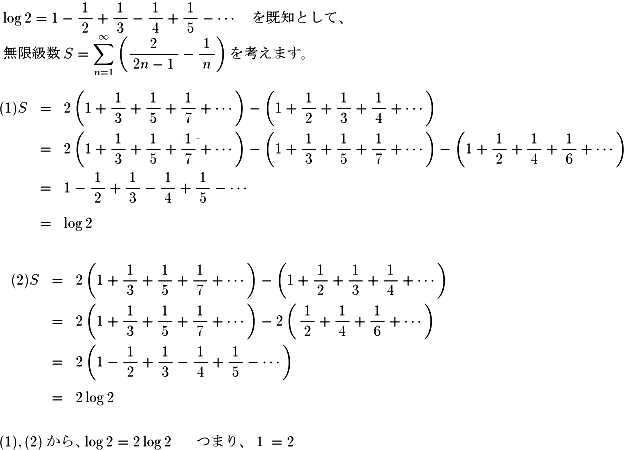
どうでしょうか? 実はこれには種も仕掛もあります。
それでもこの結果が出たときは驚きました。

NO.387 '99 3/7 ゼーター関数物語(29)
ゼーター関数ζ(2)物語第9夜の始まり、始まり。
ゼーター関数ζ(2)物語第6夜の始まりに、こんなことをかきましたね。
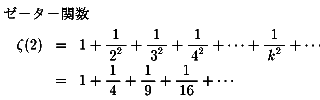
の値を追い求めていたベルヌーイ兄弟にはその和の正確
な値を出すことはできませんでした。
ヤコブは”今もって私たちの必死の探求の目をかいくぐっている、
その答えを教えてくれる人があるならば、私たちは多いに感謝する・・・”
と言い訳をしています。
ベルヌーイ兄弟は何もアイデアももっていませんでした。
ところが、『解決!フェルマーの最終定理<現代数論の軌跡>』
を読んでみると、1728年に
ベルヌーイは、この和が8/5に近いと述べたり、
1729年にゴールドバッハはこの和が1.6437と
1.6453の間にあることを言ったり、
オイラーは1731年に1.644934・・・であることをつきとめ、
結局、小数点以下20位までの和を出してみて
(コンピューターなどがなかった時代ですから、並々ならぬ計算作業です)、
それが、1.64493406684822643647・・・という数値になっていきそうだと分かりました。
そして、オイラーは「私は何度試みても、それらの和に対する近似値しか得られませんでした・・
・しかるの、まったく思いもかけず、
ζ(2)の優雅な公式を発見できました。
円周率πに関係しているのです」とその喜びを書いています。
(注:ここまで、『解決!フェルマーの最終定理<現代数論の軌跡>』を引用しました)
さて、ゼーター関数ζ(2)物語第8夜の下の問題を思い出してください。
『次の条件を満たすn次の多項式P(x)を見つけなさい。
P(0)=1、P(a1)=0,P(a2)=0,
P(a3)=0,・・・,P(an)=0』
この答えを「月の光」さんによって、解決しました。
NO.384参照ください。

無限の積と無限の和が等しくなったのですからこれ以上はない意外な結果です。 オイラーのような洞察力を持った数学者にとって、 これはおおいに示唆に富むものでした。 もう、無限の積を展開して、x2の係数を比べればよいのです。
最後の結果は読者に任せるとして、
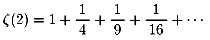
の値こそ何十年もの間数学者たちの追求を逃れ続けた値です。
それをレオナルド・オイラーは独特な方法で
ついにゼーターζ(2)の値を発見しました。
後に、ドイツの数学者リーマン(1826〜1866)によって、
次のように拡張されました。
皆さんは、リーマン積分等でご存じでしょう。
リーマン・ゼーター関数ζ(s)とは
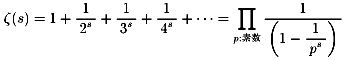
さて、今夜の問題です。
皆さんもオイラーと同じようにこの驚くべき和ζ(2)を
求めてください。この後に、次の値も工夫して求めてください。
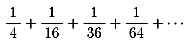
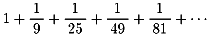

NO.388 '99 3/8 Weadore 宇宙空間での最短経路問題(5)
NO.313の答の予想です。
前回の正四面体のネットワークより、次のような
正多面体の予想を立てました。
☆予想
正多面体の最短のネットワークは、
正多面体の一面を真正面から見たときに見える輪郭の
平面図形、又はその一面自身の図形の平面図形の
最短のネットワークが成り立っているものがあり、
また、その成り立っている面の数は正n面体の場合、
n以下のnに一番近い又は同じである2のべき乗個ある。
ちなみになぜ2のべき乗を考えたかというと、
正多面体の公式、pを面数、qを角数、rを辺数とすると、
p+q−r=2が成り立つことから来ています。
これは正四面体では成り立っています。
ここで、その予想を正六面体に当てはめる。
つまり、一面を真正面に見たときにできた図形、
正方形の最短のネットワークが4個できるはずである。
ここで、正方形の最短のネットワークはシュタイナーのネットワークであり、
また、立方体の四面から見てこのシュタイナーのネットワーク
ができるのは4つが最大である事もわかる。
よって、僕の考えた予想が正しければ、正六面体の
最短のネットワークは上の条件を満たしているはずである。
このネットワークを作り、その値も計算しておくと、
一辺の長さが1の正六面体であれば、
(17-√3)/3となります。(複雑なので途中計算略)
予想の反例は歓迎です。
あと、計算もあまり自信はありません。
数学なのに字ばっかりですいませんでした。m(__)m

NO.389 '99 3/8 Idaho Potato 不思議な級数(2)
No.386の月の光さんの問題とよく似た話で、 私が知っているのは、
に対するエレガントな証明(?)です。
もちろん、月の光さんもおっしゃるように、 これには種も仕掛けもあります。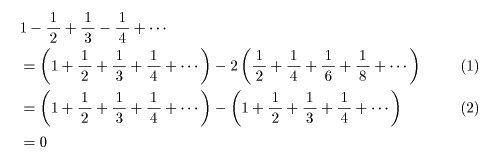
(1) すべてのマイナスの項をいったんプラスに変えて、 あとからマイナスの項を2倍して引く。
(2) ( ) の前の係数 2 を展開する。

NO.390 '99 3/9 月の光 ゼーター関数物語(30)


 E-mail
E-mail
 戻る
戻る