
Weekend Mathematics�^����^���24
�Q�S�D�����̖��

�i�y���l�|���F�����̐e������j
(1)2/3=(1/2)+(1/6)
2/3=(1/x)+(1/y)�ƍl����E�E�E�B
��������ƥ��
(2/3)-(1/x)=1/y
1/y=(2/3)-(1/x) =(2x-3)/3x�@ 1=(2x-3)
�i�y���l�|���F�R�E�X�P�j
(1)2/3=1/x+1/6
1/x=1/2
���@2/3=1/6+1/2
�i�Ȃ������Ȃ�P�^�U���o�������Ƃ����ƁA
�P�ɍ��ӂ̕��q�ƕ���̐ς��U������Ƃ���Ă݂���
���܂��������j
(2)4/5=1/20+1/y
���@1/y=3/4
3/4=1/12+1/z
���@1/z=2/3=1/2+1/6
���@4/5=1/20+1/12+1/6+1/2�@
�@
(�@)�̒��̂��Ƃ́A�@���ɋ߂����̂����邩�ȁH
�Ǝv���Ă���Ă݂܂������W�Ȃ������悤�ł��E�E�E
�i�y���l�|���F�F�� �j
�i�P�j�Q�^�R���P�^�Q�{�P�^�U
�S�^�T���P�^�Q�O�{�P�T�^�Q�O
�@�@�@���P�^�Q�O�{�P�^�S�{�Q�^�S
�@�@�@���P�^�Q�O�{�P�^�S�{�P�^�Q�@�ƂȂ芮���B
�i�y���l�|���F Hungry Bear�j
�i�P�j�@�i�P�^�Q�j�{�i�P�^�U�j
�Q�^�R���S�^�U���i�R�{�P�j�^�U
�ƍl�����̂ł������������H�H�H���܂������ł��܂���@
�i�Q�j�@�i�P�^�Q�j�{�i�P�^�T�j�{�i�P�^�P�O�j
�@�@�@�S�^�T���W�^�P�O���i�T�{�Q�{�P�j�^�P�O
�i�y���l�|���F�݂� �j
2/3=1/2+1/6
4/5=1/10+1/5+1/2
���Ƃ���4/5�̏ꍇ4/5=8/10
10�̖�1.2.5��1.2.5�̑����Z�̑g�ݍ��킹��8�ɂȂ���̂�T����
1+2+5�ł��B
�����8/10=1/10+2/10+5/10
���q�͂P�O�̖��������ƕK�����q�͂P�ɂȂ�܂��B
�i�y���l�|���F�n�� �j
�i�P�j�Q�^�R�ōl����ƂP�^�R�{�P�^�R���������ł����A�������A����͂ӂ��킵��
�Ȃ��B
������A�܂��́A�����L���čl���₷������B
�Q�^�R���S�^�U�ɂ��čl���Ă������B
�S�^�U�̏ꍇ�A�S�^�U���P�^�U�{�R�^�U�@�Ƃ��������ł��A
�S�^�U���P�^�U�{�P�^�Q�@�ƂȂ�A�܂��P����
�S�^�U�ł͂����ł��Ȃ�����A�Q�^�R������ɂU�^�X�Ƃ��čl���Ă����B
�U�^�X�̏ꍇ�A�U�^�X���P�^�X�{�T�^�X�@�Ƃ��������ł���B
���A�T�^�X�͂ӂ��킵���Ȃ��B����āA
�U�^�X���P�^�X�{�P�O�^�P�W
�@�@�@���P�^�X�{�i�P�^�P�W�{�X�^�P�W�j
�@�@�@���P�^�X�{�P�^�P�W�{�P�^�Q�@�ƂȂ�܂�����
����ɍL���āA
�U�^�X���P�^�X�{�P�O�^�P�W
�@�@�@�@�@�@�@�@�@�@���P�^�X�{�i�R�^�P�W�{�V�^�P�W�j
�@�@�@�@�@�@�@�@�@�@���P�^�X�{�P�^�U�{�P�S�^�R�U�@
�@�@�@�@�@�@�@�@�@�@���P�^�X�{�P�^�U�{�i�Q�^�R�U�{�P�Q�^�R�U�j
�@�@�@�@�@�@�@�@�@�@���P�^�X�{�P�^�U�{�P�^�P�W�{�P�^�R�@�ƂȂ�܂�����
���̗v�̂ł���Ă����܂����B
�i�y���l�|���F ����܁j
���̎菇�ŋ��߂܂����B
��j���`�^���a�����P�^���a�{���R�^���a�{���S�^���a
�@�@�@���P�^�b�{�P�^�c�{�P�^�d
�i�b�A�c�A�d�͂��a�̌��ɂȂ�j
���ۂɖ��������Ă݂܂����B(1)�Q�^�R�Ƃ���ŁA�P�ʕ����ł���킹�Ȃ������͂���̂ł��傤���H
�Q�^�R���S�^�U �@�@�@���R�^�U�{�P�^�U �@�@�@���P�^�Q�{�P�^�U �i�����j �܂��� �Q�^�R���W�^�P�Q �@�@�@���S�^�P�Q�{�R�^�P�Q�{�P�^�P�Q �@�@�@���P�^�R�{�P�^�S�{�P�^�P�Q �i�����j (2)�S�^�T �S�^�T���W�^�P�O �@�@�@���T�^�P�O�{�Q�^�P�O�{�P�^�P�O �@�@�@���P�^�Q�{�P�^�T�{�P�^�P�O �i�����j �܂��� �S�^�T���P�U�^�Q�O �@�@�@���P�O�^�Q�O�{�T�^�Q�O�{�P�^�Q�O �@�@�@���P�^�Q�{�P�^�S�{�P�^�Q�O �i�����j �܂��� �S�^�T���Q�S�^�R�O �@�@�@���P�T�^�R�O�{�U�^�R�O�{�Q�^�R�O�{�P�^�R�O �@�@�@���P�^�Q�{�P�^�T�{�P�^�P�T�{�P�^�R�O �i�����j �܂��� �S�^�T���Q�S�^�R�O �@�@�@���P�T�^�R�O�{�T�^�R�O�{�R�^�R�O�{�P�^�R�O �@�@�@���P�^�Q�{�P�^�U�{�P�^�P�O�{�P�^�R�O �i�����j
1/2+1/3+1/4+1/5+1/6+1/7+1/8+1/9+��1/2+1/4+1/4+1/8+1/8+1/8+1/8+1/16+�c ��1/2+1/2+1/2+1/2+�c�������ƁA�P�ʕ����̘a�͔��U����̂ŁA �ǂ�ȕ����ł��\�������ȋC�����܂����A�ǂ��Ȃ�̂ł��傤�B
�i�y���l�|���F���肳�̂������� �j
�����̖��C�����������ς�����̂ŁC
�����ɂł��邱�Ƃ̐������l���Ă��܂����B
�ꉞ�ł����̂ŁC�����肵�܂��B
�ŏ��́C�u�Ƃɂ�������Ă݂�v�ł��B
�i�P�j 2/3��P�ʕ����̘a�ŁC
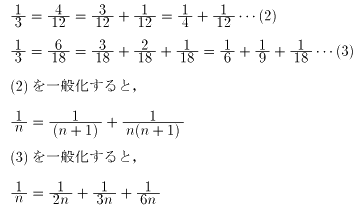
�i�y���l�|���F���̗��� �j
�i�y���l�|���F�}�T�{�[ �j


�i�y���l�|���F���̌� �j


�֘A�������e��
�R���L�E������NO.250�ɂ���܂��B
�i�y���l�|���Fakihiro�j
�܂��i�P�j�ł����A�Q�^�R���P�^�Q�{�P�^�U��
�Q�^�R���P�^�R�{�P�^�S�{�P�^�P�Q�Ƃ��B
�i�Q�j�S�^�T���P�^�Q�{�P�^�T�{�P�^�P�O�A
�S�^�T���P�^�Q�{�P�^�S�{�P�^�Q�O�ȂǁB
���ߕ��́A�Ƒ�����܂�Ȃ��ł��i�j�قځA�������ł��B
�Ⴆ�A�i�P�j�̏ꍇ�B
�Q�^�R���P�^�Q�{�P�^�U�Ƃ������������܂������A
����͈ȉ��̂悤�ɋ��߂܂����B
�܂��A�Q�^�R����P�^�Q�������܂��B�c��̂͂P�^�U�B
����ĂQ�^�R���P�^�Q�{�P�^�U�ł��B
�ǂ��ł����A�������ł��傤�i�j
�ł��A������ƍl���܂����B���ꂾ���ł͂Ȃ����낤�A�ƁB
�����ŁA�P�^�S�������ƁA�T�^�P�Q�A
�܂�T�^�P�Q�𑼂̒P�ʕ����ŕ\�����Ƃ��ł���A
�����Ƃ���킷���Ƃ̏o���鐔�͂���̂ł͂Ȃ����Ǝv�����̂ł��B
�Ă̒�A�T�^�P�Q�͂P�^�R�{�P�^�P�Q�Ƃ���킷���Ƃ��o���܂����B
���Ȃ݂ɁA���̋��ߕ��́A�T�^�P�Q��
�P�^�P�Q�{�P�^�P�Q�{�P�^�P�Q�{�P�^�P�Q�{�P�^�P�Q�ƍl���A
�O�̂S���܂Ƃ߂�ƂS�^�P�Q�{�P�^�P�Q�A
�܂�P�^�R�{�P�^�P�Q�Ƃ����A��̂����������ōl���܂����B
�i�Q�j�̕����قړ����l�����ł��B
���̂悤�ɍl����ƁA����͖����ɂ���̂ł͂Ȃ��ł��傤���ˁB
�i�y���l�|���F�Q���ڂ̎R�c �j
�P�A�P�^�Q�{�P�^�U
�Q�A�P�^�Q�{�P�^�T�{�P�^�P�O�ł��B
�����͌��������ŕ��������������ł����E�E�E�E
�������́A�����Q�C�R�C�S�C�E�E�E�E��
�P�^���Ђ��ĕ��ɂȂ�Ȃ��Ƃ�����Ƃ��Ă�������Ȃ��ł��傤���B
���ꂪ����܂�ł����������Ƃ��C�ɂȂ�܂��B
�i�y���l�|���FIdaho Potato�j
����͂ƂĂ������̔Z��mail���������������܂����B
�u�C�ӂ̕���(���m�Ɍ����Ɛ��̗L����)�͕K��
�قȂ�P�ʕ����̘a�Ƃ��ĕ\�����Ƃ��ł���v���ؖ����܂��B
�^����ꂽ�������Ȃ��P�ʕ����̒��ň�ԑ傫�����̂������Ă����܂��B
��������J��Ԃ��ƁA�K���c����P�ʕ����ɂȂ�܂��B

�֘A�������e��
�R���L�E������NO.254�ɂ���܂��B
��̓I�Ȗ��Ɏ��g�ގ��́A�ȉ��̕\�����ɂ��Ǝv���܂��B
| N | 1/N�@ | N | 1/N�@ | N | 1/N�@ | N | 1/N�@ |
|---|---|---|---|---|---|---|---|
| 1 | 1.00000�@ | 11 | 0.09091�@ | 21 | 0.04762�@ | 31 | 0.03226�@ |
| 2 | 0.50000�@ | 12 | 0.08333�@ | 22 | 0.04545�@ | 32 | 0.03125�@ |
| 3 | 0.33333�@ | 13 | 0.07692�@ | 23 | 0.04348�@ | 33 | 0.03030�@ |
| 4 | 0.25000�@ | 14 | 0.07143�@ | 24 | 0.04167�@ | 34 | 0.02941�@ |
| 5 | 0.20000�@ | 15 | 0.06667�@ | 25 | 0.04000�@ | 35 | 0.02857�@ |
| 6 | 0.16667�@ | 16 | 0.06250�@ | 26 | 0.03846�@ | 36 | 0.02778�@ |
| 7 | 0.14286�@ | 17 | 0.05882�@ | 27 | 0.03704�@ | 37 | 0.02703�@ |
| 8 | 0.12500�@ | 18 | 0.05556�@ | 28 | 0.03571�@ | 38 | 0.02632�@ |
| 9 | 0.11111�@ | 19 | 0.05263�@ | 29 | 0.03448�@ | 39 | 0.02564�@ |
| 10 | 0.10000�@ | 20 | 0.05000�@ | 30 | 0.03333�@ | 40 | 0.02500�@ |

�Ƃ����킯�Łu���̗���v����(���̃G�l���M�|�ɓ���������܂��B)�قǂł͂Ȃ��ɂ��Ă��A
������ł��ł��Ă��܂��Ƃ������������܂��B
�u�\�����������ɂ���v�Ƃ����_�ɂ��ẮA
�u���肳�̂�������v����A�u�}�T�{�[�v����A�u���̌��v����
��̓I�ȍP��������Ă��������܂����B
���̖����ɂ���\�����̒��ŁA�P�ʕ����̌��������ɏ��Ȃ����邩�A
�����Ă��̍ŏ����͂������H�@�Ƃ����₢�������u�}�T�{�|�v����
�Ȃ���Ă��܂��B
����ɂ��ẮA��L�̂����ł܂��P�ʂ�ۏ��Ă����āA
���̌��ȉ��̏ꍇ�ɂ��Ă͕������łȂ����Ƃ�(���邩���H)
�m���߂邵���Ȃ��悤�ȋC�����܂��B
�ǂȂ����A�킩�����狳���Ă��������B
�Q���ڂ̎R�c
���̗���
�}�T�{�[
Hungry Bear
akihiro
�F��@�q
�n��
���肳�̂�������
�R�E�X�P
Idaho Potato
�����̐e������
�����
�݂�
���̌�
 �߂�
�߂�