
Weekend Mathematics/コロキウム室/1999.1〜3/NO.35
NO.274 '99 1/12 月の光 1999年の問題(5)


NO.275 '99 1/12 Junko 定義域(2) 定義域というのは文字通り「定義」するものですから、自由に設定できるはずです。
従ってこの問題は最大限定義できる範囲と解釈することにします。
逆関数を考えて、その値域(Yのとりうる範囲)を求めればいいのでしょうか?

こちらの定義域は、x>0と考えられますから、
この時の値域を考えることにします。

NO.276 '99 1/12 月の光 四角形の最大値(1) 中心Oの円Oがあり、半径をrとする。
円Oの周上の一点aを中心とする円Aと円Oが交わる2点を順にb、dとする。
次に、a,oを結ぶ直線と交わる点をcとする。
この時、四角形abcdの最大値を求めよ。
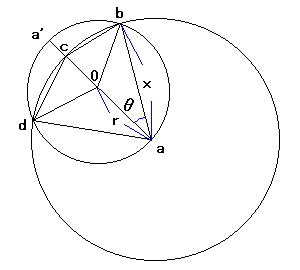
円Aの半径をxとし、0<x<2rとする。
左図のように∠oab=θ、0<θ<(π/2)としてみてください。
これは、大学院の入試問題ですが、意外と簡単です。

NO.277 '99 1/13 水の流れ 1998倍数の問題(2) 2.1998=2×9×111 で偶数なので、
等しい各位の数字は、2,4,6,8が考えられる。
ところが、2,4,8の3つの場合、
これらを並べた数が9の倍数でもあるので 最低9桁は必要です。
実際並べてみます。 3.1998より大きい自然数Nを考えると、
組み合わせの記号NC1998は
222222222,444444444,888888888
は1998で割り切れない。
一方、666666666は1998で割り切れる。
さらに、6666,66666,6666666,
66666666は明らかに9の倍数でない。
666666は999の倍数でない。
したがって、 答え 666666666
NC1998=
N(N−1)(N−2)・・・(N−1997)/1998!
ここで、左辺はN個のものから1998個とる組み合わせの数だから
自然数であり、これは右辺の分子が(連続する1998個自然数の積)
1998!で割り切れることを示しています。
よって、証明終わり。
「一般に連続するn個の自然数の積はn!で割り切れます。」

NO.278 '99 1/13 水の流れ 星形n角形 正n角形があります。
今、1つの頂点から出発し、等しい長さの対角線
を右まわりに連続して次々に引いていきとき、
何周かして元の点に戻るまでに、
すべての頂点を通過している場合があります。
こうして、これらの線によって1つの模様が出来ます。
この模様を星形n角形と呼びます。
例えば、n=5のとき、皆さんがご存じの星形1個ができます。
n=6のとき、星形6角形は出来ません。
さて、n=7のとき、異なる星形7角形は何個できますか。
n=10のとき、異なる星形10角形は何個できますか。
n=12のとき、異なる星形12角形は何個できますか。
一般に、異なる星形n角形は何個できるか、nで表してください。

NO.279 '99 1/13 Junko 定義域(3)

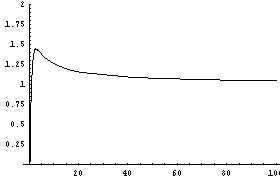
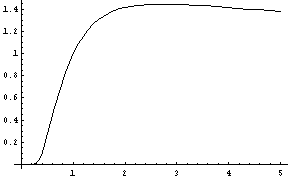


NO.280 '99 1/14 Idaho Poteto 分数の問題・その後(6) No.261で、マサボーさんは、
「分数の問題」に対する「数学的に正しい解答」とは何かを論じておられますが、
この点について、私はかなり異なる見解を持っています。
今回の問題は、「2/3, 4/5 を、相異なる単位分数の和で表せ」というものでしたが、
私は、問題文を読んで、単純に、
それを超える部分は、
あくまで、
それぞれの解答者による独自の拡張であって、
それはそれで大いに有意義なことではありますが、
問題に対する答としての「正しさ」とは別次元の話だと思います。
したがって、この問題の答としては、
少なくとも(たとえば)「2/3 = 1/2 + 1/6」「4/5 = 1/2 + 1/5 + 1/10」の2つの事実が述べられていれば、
それだけで完璧に「数学的に正しい」と考えます。
ついでに言うと、私は、
「1/2 + 1/6」「1/2 + 1/5 + 1/10」という具体的な解を「どうやって見つけたか」ということは、
その解答の「数学的な正しさ」とは無関係だと思っています。
つまり、たとえ「あてずっぽう」でそれらの解を見つけたとしても、
結果さえ正しければ、それは「数学的に正しい」、ということです。
このようなことを言うと、
見識高い「数学教育者」の皆さんのお叱りを受けるかもしれませんが、
数学一般において「正しい」とはそういうことである、
ということも、また事実なのです。
この問題が要求していることは、
2/3, 4/5 のそれぞれについて、
単位分数の和による表現を「少なくとも1通り」示すことである
と理解しました。
「すべての解を示せ」と明示的に要求していない以上、
このような解釈は、数学的に自然だと思います。
そして、その「拡張」の例として、たとえば
などがあるわけですが、
具体的に与えられた分数について、
単位分数の和による表現をもれなく検索するための手順を与える
ということもまた、その「拡張」のひとつとして評価されるべきだと思います。
もちろん、より一般性のある解法を示すほうが、
「より多くの拡張の可能性が生じる」という意味において有益であることは、
私も十分承知しています。
しかし、そのことと、
答としての「正しさ」とは、別の問題であると理解しています。

NO.281 '99 1/14 Idaho Poteto 分数の問題・その後(7) 前項に関連する問題提起です。
次のような問題を考えます。
この問題に対する解答例を2つ示します。
どちらのほうが、より「数学的に正しい」解答といえるでしょうか?
したがって、命題「x2 > 4 ならば x > 2」は正しくない。
したがって、命題「x2 > 4 ならば x > 2」は正しくない。

NO.282 '99 1/14 3−6 定義域(4)
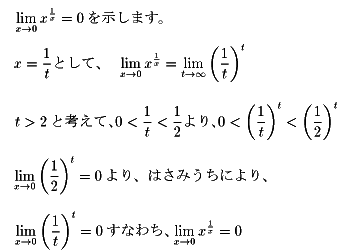

NO.283 '99 1/14 I.T. 定義域(5)


NO.284 '99 1/14 水の流れ 定義域(6)

 E-mail
E-mail
 戻る
戻る