NO.1871 電磁気学Minimum-8（エネルギー保存則-1） 2010.8.31. ＤＤＴ
以後、NO.1744 ベクトル解析Minimum(1)，
NO.1749 ベクトル解析Minimum(2)，
NO.1752 ベクトル解析Minimum(3)，
NO.1757 ベクトル解析Minimum(4)の式は、無条件に使います。
今回は、荷電粒子と電磁場を含む系を扱い、エネルギー保存則を導く事が目標です。ここでエネルギーには、荷電粒子の（質点の）運動エネルギーと電磁場のエネルギーの両方が含まれますが、最後まで行けませんでした。まず「エネルギー保存則って何？」という前振りをやり、その次に「当たり」を付けるために、流体力学に寄り道します。
１．荷電粒子と電磁場を含む系
NO.1854 Minimum-7で注意したように、荷電粒子と電磁場を含む系において、荷電粒子の運動を定めるためには、電磁場に関するMaxwell方程式だけでなく、粒子に対するNewtonの運動方程式も必要です。ここで荷電粒子に働く力は、Minimum-3でやったように、電場Ｅと磁束Ｂによって決まるLorents力です。重力は無視します。
NO.1767 Minimum-3によればLorents力は、速度ｖと電荷eを持つ荷電粒子に対して、
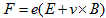
です。よって系内に複数個の荷電粒子があるとすれば、ｉ番目の荷電粒子の運動方程式は、
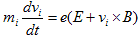(N-1)
となります。ただしｉ番目の荷電粒子の質量をｍｉ，速度をｖｉとしました。電荷については、荷電粒子とは具体的には電子の事なので、その素電荷は全てeに等しいとします。
一方Maxwell方程式ですが、その中に現れる電流密度ｊと電荷密度ρは、
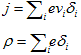
δｉは、荷電粒子の位置に特異点を持つデルタ関数で、上記は単位を調べれば了解できると思います。
従ってMinimum-7.1.(M-1)〜(M-6)より、荷電粒子と電磁場を含む系のMaxwell方程式は、
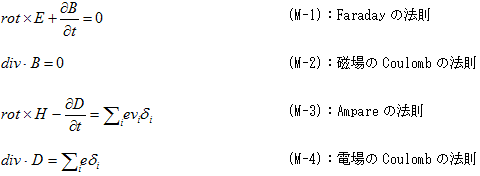
となります。磁場Ｈと磁束Ｂ，電場Ｅと電束Ｄの関係は以下です。
ここに、
ε0：真空の誘電率
μ0：真空の透磁率
２．ところでエネルギー保存則とは何？
ところでエネルギー保存則とは何でしょう？。もっと言えば、エネルギーとは、仕事とは何でしょうか？。エネルギー＝仕事でしょうか？。実際、単位は同じです。
結論を言うと単位は同じですが、エネルギーと仕事は同じではありません。No.1668で述べたように、
・仕事はエネルギーではありません．
・仕事とは、エネルギーの移動量を表わしたものです．
ではエネルギー保存則とは？。
・仕事の受給関係が（エネルギーの移動関係が）、時間的に不変である事を述べたもの．
です。実際に、保存力のもとで運動する質点のエネルギー保存則を導いてみます（初速度0）。
xを質点ｍの変位ベクトル，Ｖ(x)を保存力のポテンシャルとして、運動方程式は、
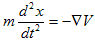
となります。両辺にｖ＝dx/dtをかけ、時間で積分すれば、右辺は保存力が質点に対して成した仕事です
（・は内積を表します）。
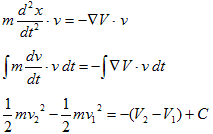
最後の式には、Ｖがポテンシャルである事を使いました。Ｃは積分定数です。
Ｖ1は初期位置でのポテンシャルエネルギー，
Ｖ2は運動後のポテンシャルエネルギーです。
一般に運動は、ポテンシャルエネルギーの高い方から低い方へ起こるので、
Ｖ2＜Ｖ1です。
つまり、−(Ｖ2−Ｖ1)＞0で、これだけのエネルギーが、仕事として運動エネルギーへ供給されたと読めます。右辺第1項を左辺へ移項し、時間で微分すれば、
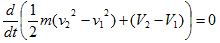
となりますが、ポテンシャルの不定性から、Ｖ1＝0とできます。またｖ1=0です。
そうするともはやＶ2，ｖ2書く必要もなくなるので、
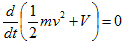
が最後の形です。つまり、
・仕事の受給関係が（エネルギー移動関係が）、時間的に不変である事．
が言えました。ここがポイントです。
以上の事は、荷電粒子と電磁場を含む系のエネルギー保存則を導く上で、手掛かりになります。エネルギー保存則とは「仕事の受給関係が時間的に不変である事」を言うものです。
・では、荷電粒子と電磁場を含む系において、「仕事をされる側」と「仕事をする側」は何でしょうか？。
・保存力とのアナロジーで言えば、質点と電磁場となります。
それが1.(N-1)です。何故ならLorents力は、その時の電場Ｅと磁束Ｂ、すなわちその時の電磁場の状態で決定されるものだからです。
従って、(N-1)の両辺に荷電粒子の速度を掛け時間で積分すれば、右辺は電磁場が荷電粒子に対して成した仕事に等しく、その受給関係が時間的に不変ならば、エネルギー保存則です。
少しだけやってみます。1.(N-1)の両辺に、ｖｉを掛ければ（・は内積）、
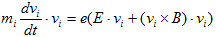
です。(ｖｉ×Ｂ)とｖｉは明らかに直交するので、
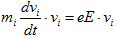(1)
です。 そしていま欲しいのは、全荷電粒子を含むエネルギー保存則です。なので(1)のｉに関する和を取ります。
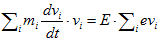(2)
しかし(2)の右辺は、ＥとＢだけで決定されていません。ｖｉが残っています。
ｖｉを消去しなければ、電磁場が荷電粒子に対して成した仕事かどうかはっきりしません。そこで1.(M-3)を利用します。
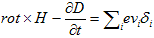(M-3)：Ampareの法則
(2)と(M-3)を結びつけるために、(2)をデルタ関数表示に戻します。デルタ関数の性質より、
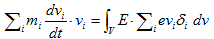(3)
が得られます。ここで(3)の積分領域Ｖは、荷電粒子ｍｉを全て含む任意の体積です。(3)と(M-3)を結びつけるために、(M-3)の両辺に電場Ｅを掛け、その体積Ｖで積分します。そうすると、
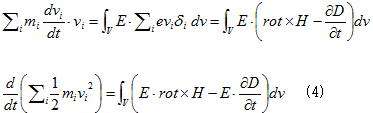(4)
となりますが、(4)以降の変形はかなり大変です。大変なのですが、(4)の右辺は電場Ｅ（Ｄ）と磁場Ｈ（Ｂ）のみで表わされており、右辺は、電磁場が荷電粒子ｍｉに対して成した仕事だと読めます。つまり、(4)は仕事の受給関係を表わすものです。(4)の関係が時間的に不変であれば、エネルギー保存則です。
３．連続体力学への寄り道
2.(4)以降の変形はかなり大変です。大変なので、連続体力学へ寄り道して「当たり」をつけます。
Maxwell方程式が発表された19世紀当初において、電磁場の時間発展（運動）とは、一種の連続体力学とみなされていました。その最先端は、イギリスのケルビン（JJ･トムソン卿）です。
連続体力学とは、固体力学の事です。固体力学とはつまり、物質の塊りがある力を受けた時、どのように振る舞うかを記述するものです。固体は連続的に分布する「質量密度」の塊りなので、その微小部分にNewtonの運動方程式を適用すれば、正解が得られるはずだ！、というのが連続体力学の基本的発想でした。Newtonの運動方程式が正しい以上、この発想は正しいですし、今でも現役の理論です。今では「材料力学」とも言われ、全ての土木・建築・機械工学の設計計算の基礎です。
・連続体力学は、19世紀には実証されていました．家屋，建物，堤防，橋，道路、いわゆる土木・建築の設計と施工において．また機械工学と工作において．
Maxwell方程式（電磁場の運動方程式）が、連続体力学の一部とみなされたのには訳があります。Minimum-7でもやったように、Maxwell方程式は電磁場の波動方程式を導きます。
そして連続体力学が信じられて、電磁波という波が「真空」を伝わるならば、波の運動を伝える「何か」が真空になければいけない、というわけです（これが物理です）。それが全宇宙に充満する、エーテルという物質でした。そして、エーテル波動としての電磁波は、連続体力学の理屈に従って伝わるはずだと・・・。
エーテルとは、Maxwell方程式の通りに電磁場の波動を伝える「何か」でした。色々と調べると、エーテルは、ふつうの物質では決してあり得ないという事になったのですが、それでも、実験的にそれが否定されない限り、それを支持するのも物理学です（これも物理です）。それを否定したのは、マイケルソン・モーリーの実験とアインシュタインでした（ここは省略します）。
何を言いたいかというと、Poynting（ポインティング）さんが、電磁場のエネルギー保存則を導いた当時の雰囲気は、電磁場の連続体力学的解釈が、全盛だったという事です。当然、電磁場のエネルギー保存則を導くにしても、連続体力学的発想を使ったはずです。
それに習ってみようじゃないか！、という話です。そうなると、当時の連続体力学の代表は何か？、となります。弾性学と流体力学です。ここでは流体力学、その中でもとりわけ簡単な、非圧縮性完全流体を採用します。ちなみに、せん断抵抗しない固体が流体（液体）です。
非圧縮性完全流体を扱う分野は、いちおう水理学とも言われ、水道管とか下水管とか河川設計（堤防）にとか、要するに全ての水まわりを扱うものです。扱えないと世界のインフラは、今すぐにでも崩壊します。
４．流体の運動方程式
非圧縮性完全流体とは、ふつうの水の事です。ふつうの水は極めて圧縮（伸長）されにくいので、それの理想化が非圧縮性です。完全とは、水の運動に摩擦なしという意味です。これにも理由があって、水の摩擦（粘性）効果が顕著になるのは、河であれば岸辺に貼りついたような、非常に薄い水の層に限られます（薄いとは、河の全幅に比較してです）。河全体の状態を調べるなら、非圧縮性完全流体で十分だというわけです。以下ではやや天下りですが、必要な式は都度導入します。
最初に、流体力学の物理量を定めます。それは水の速度ｕ（流速）です。河を想像すればわかるように、流速は場所ごとに異なります。また同じ場所であっても、時刻によって流速は変化します。従って流速ベクトルuは、場所と時間の関数です。
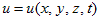(1)
流速を場所と時間の関数として計算できれば、現在のある場所の流れの様子は完全にわかりますし、水塊の全ての点の流速を時間に沿って追っていけば、例えば津波の進行がわかり、津波の変形つまりは波高もわかります。流体力学の全ては、uを計算する事に尽きます。
連続体力学の基本仮定は、連続体の微小部分にNewtonの運動方程式が成立する、です。Newtonの運動方程式は加速度に関するものです。そこで流体の微小部分の（1点の）加速度を計算します。それは速度ベクトル（u）の時間微分です。
注目している微小部分が、ある時刻tに、(1)の(x，y，z)の位置にいたとします。微小時間dt後には、
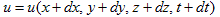(2)
に移動します。(2)と(1)の差が、速度ベクトルｕの時間間隔dtの間の増分であるのは、明らかと思います。
ｕ＝(ux，uy，uz)と成分表示すれば、全微分を使って、
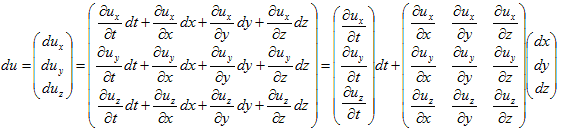(3)
と書けます。
最右辺の1項目のベクトルを、∂u/∂tで略記します。2項目の行列の各行は、ux，uy，uzの勾配になっています。そこで、
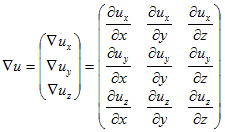
の事だと決めておいて、(3)を、
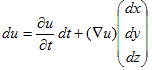(4)
と略記します。∇uは、なんの事はない、uのヤコビ行列です。
(4)を微小時間dtでわれば、加速度です。実際、
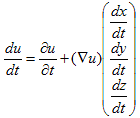
ですが、(dx，dy，dz)は、考えている微小部分が、時間間隔dtの間に動いて行った、走行距離です。従って、
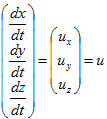
は明らかなので、
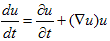(5)
が加速度、という事になります。これに質量をかければｍａ＝Ｆのｍａが得られた事になりますが、いまは微小体積を考えているので、微小体積中の平均質量を使います。それが密度ρです。ところが水のρは1で（全物質に対する密度の基準）、どこでも一定です（これには非圧縮性が関係します）。よって(5)は、ｍａそのものです（単位は変更しますけど）。
次はＦの番です。流体中では圧力Ｐ（スカラー）が働きます。微小体積を考えてみれば、微小体積の上下と左右では逆向きの圧力になっています。つまり圧力の作用とは、その圧力差だけです。それでｍａ＝Ｆは、
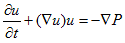(6)
となります。完全流体の場合、摩擦は考えないので、運動方程式(6)に、これ以上加えるものはありません。
あと書いておかなければならないのは、非圧縮性です。ベクトル解析Minimumの中でやったように、湧き出しも吸い込みもなければ、それは、
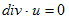(7)：流量保存則
と書けます。あと(6)，(7)とは別に、ｕからＰを決定する圧力方程式が必要ですが、ここでは省略します。
５．流体の運動方程式を観察してみる
4.(6)を観察するために、それをある体積Ｖで積分してみます。
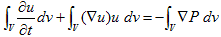(1)
4.で述べたように圧力Ｐは、圧力差∇Ｐを導くポテンシャルです（ポテンシャルエネルギーではありません。だいたい単位が違います）。よって(1)の右辺は、
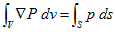(2)
になります。ここでＳはＶの表面，dsはＳの面素ベクトルです。(2)には、ポテンシャルの積分は経路に依存しないという、ポテンシャルの定義を使っていますが、余り詮索するのはよしましょう。この話は、あくまで「当たり」を付けるためのものですから・・・。さらに∂/∂tは、積分の外に出せます。
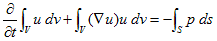(3)
単位と矛盾する事をあえて無視して意味を言うと、(3)の右辺は、体積Ｖの表面に働く表面力の合力になっています（合力という結果は正しいです）。(3)で、左辺第2項がないとします。
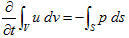(4)
(4)は、体積Ｖを1個の質点のように考えた時、その全運動量（ｕの体積積分）の時間変化は、表面に作用する（外から作用する）外力に等しい、と読めます（この場合も、体積積分が運動量になる事は正しいです）。これは、体積Ｖを1個の質点のように考えた時の、運動方程式の意味そのものです。
以上を念頭に置きつつ、(3)の2項目を右辺へ移項します。
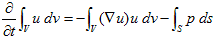(5)
(5)の右辺1項目は、体積Ｖを1個の質点のように考えた時、その全運動量の時間変化に寄与するものです。つまり1項目は、表面力のように振る舞う「何か」です。何を言いたいかというと、そうであれば右辺1項目は、表面積分に直せるに違いない、という事です。次の関係式があります。
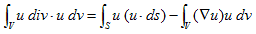(6)
(6)は、ガウスの発散定理の部分積分版ですが、微分形式を熟知していると、すぐわかります。自分は熟知していないので、テンソル記法で追いかけて確認しました。カッコつけてテンソル記法などと言いましたが、要するに成分に書き下して導いた、という事と同じです。(6)を、(1)に代入すれば、
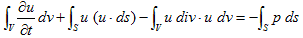(7)
(7)の左辺第3項の体積積分は、4.(7)より0です。従って、
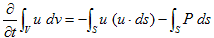(8)
が得られます。(8)の右辺第1項は、表面力と等価なものです。これには、質量が変化する質点の運動方程式に対応物があります。
質点の運動方程式は、質量が変化しない場合を扱うのが普通ですが、質点に加えられた力積が質点の運動量変化に等しいという、本来の意味を思い出せば、d(ｍｖ)/dt＝Ｆなので、
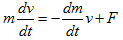(9)
になります。(9)の右辺第1項が、(8)の右辺1項目に，(9)の右辺第2項が、(8)の右辺2項目に対応しますが、後半は明らかと思います。前半が何故対応するかと言うと、(8)の各項には、質量密度ρ＝1がかかっている事を思い出して下さい。そしてｕが一様流れ、つまり場所によらずｕ＝一定の場合を考えます。
Ｓの面素（微小面積）daを横切ってＶから出て行く質量の流出速度の合計は明らかに、
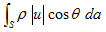(10)
です。(10)はベクトル解析Minimum-1で示しました。同じところで、面素と面素ベクトルの関係は、ｎをＳの外法線単位ベクトル，θをｕとｎの成す角として、
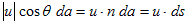
でした（という風に、Minimum-1の内容を読んで下さいね^^）。よって(10)は、
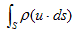(11)
となり、(11)はＶから出ていく質量の流出速度の合計です。(9)ではこれが、dｍ/dtで表わされています。
いまｕ＝一定なので、Ｖから出ていく運動量の流出速度の合計は、流出質量ρ(ｕ・ds)dtが速度ｕを持つので、
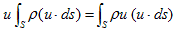(12)
です。意味を考えれば、(12)の右辺は、ｕが一定でない場合にも使えます。(12)の結果は、一つのベクトルｖを決定します。(9)ではこれが、
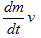
と表わされてるだけです。
これで、Ｖを1個の質点のように考えた時、(8)の右辺第1項は、(9)の右辺1項目と同じものだ、という事はわかって頂けると思うのですが、何故質点からの質量流出（運動量流出）が、力と等価なのか、という疑問は残ります。
現実には質点から質量が流れ出すためには、何らかの流出機構が必要です。しかし質点に、「機構」は考えにくいです。大丈夫です。(9)は別に質点に限った式ではありません。こんな例はどうでしょう？。
貨車の上で「自分が」、砲丸を投げた時を想像します。「自分は砲丸を投げるために」、貨車を「蹴る」はずです。「蹴った事」によって（その反作用によって）、貨車は逆向きに「動く」はずです。そりゃそうです。自分は足の裏で貨車に、「力」を及ぼしたのですから。こんなのは、すぐ実験できます。
公園の池の手こぎボートの上で前に飛んだら、ボートは後ろへ動きます（オールで掻いてもいないのにです。でも危険だからやめて下さい）。次に、10tのピンポン球と、ピンポン球投射機を積んだ貨車を考えます。
ピンポン球投射機は猛烈な勢いでピンポン球をy方向へ投射する、とします。投射機は、砲丸を投げた「自分といっしょ」です。投射機を貨車に固定する、ボルトかリベットを通じて、投射の際の反動（反作用）が、貨車に、「−y方向」に「力」として伝わります。
力は、単位時間当りに投射するピンポン球の量が多いほど、ピンポン球に与える速度が大きいほど大きくなります。要は、dｍ/dtかけるｖです。
つまり(9)のｍは、物体の質量に読み替えられます。物体は体積Ｖを持つので、物体を体積Ｖに読み替えても良いのは、明らかです。そして、(8)と(9)の両方から同じ結果が出ます。
積荷（ピンポン球）の質量も考慮した、「現在の」貨車の質量をｍとして、
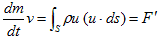(13)
です。ここでρは、ピンポン球の山の（積荷の）体積から計算できる、ピンポン球の質量密度，uは個々のピンポン球の速度，Ｓは貨車の外壁に沿って取った体積の表面です。
(13)は全て、「力として」として貨車に作用するものでした。(13)の結果得られる「力」Ｆ’を貨車に外力（表面力）として加えても、貨車は全く同じように動きます。これが、(8)の右辺第1項を、表面力と等価なもの、と考えて良い理由ですが、実際にはそれ以上です。
(8)の右辺第1項は、表面力そのものです。何故なら流体の場合、流速によって生じた流体各部分の「押し合いへし合い」の結果として質量流出が起きるので、体積Ｖの表面は、針鼠のように噴射ノズルを（投射機を）持つような状態だからです。
ところで以上は、投射機構の内部とは無関係な結果です。投射機構が、どんなに複雑な部品や内部機構から組み立てられていようと、その部品や内部機構は、その隣の部品や内部機構に、全部集めれば投射運動量に等しい力積を伝達します。それが作用反作用の法則です（部品どうしの押し合いへし合い）。従って最終的には、投射機を貨車に固定するボルトやリベットを通じて、10tのピンポン球全てに与えた運動量が、貨車へ伝達される事になります。この運動量の増加によって、貨車は「−y方向へ」動きます。
さらにピンポン球を気体分子としても良いはずです。また、気体分子を投射する投射機構の内部は(13)の結果と無関係なので、それが、圧搾空気に混合された燃料噴霧ガスの爆圧の結果でも良い事になります。これが、ジェット機やロケットの動く（推進力の）原理です。
ジェット機やロケットは、噴射媒体（高速気流の気体分子）の大気との衝突の反作用で動いているのでは、ないです。運動量の投射によって動いています。だからロケットは、大気のない宇宙空間でも「進みます」。
・・・ところでそれは良いんだけど、エネルギー保存則は？。
６．非圧縮性完全流体のエネルギー保存則
エネルギー保存則を導くために、もう少し手を加えます。今度は体積Ｖの中に、1個の物体が含まれるとします。物体は変形せず、質量はｍです。
物体体積の表面Ｔを考慮すれば、5.(8)は、
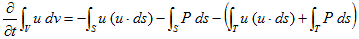(1)
と書けます。(1)左辺の体積Ｖは、物体分を除いた領域です。右辺の括弧の部分は、流体が物体から受けた表面力です。何故なら括弧を発生させる物理的原因は、物体しかないからです。作用反作用の法則より、物体には逆向きの力が働きます。
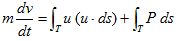(2)
次に物体は、その表面を流れる流速が一定とみなせるくらい、十分小さいとします。つまり物体表面に限っては、ｕ＝一定です。そうすると、(2)の右辺第1項は、
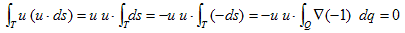(3)
と変形できます。ただし物体の体積をＱとし、最右辺に5.(2)を使いました。−が付くのは、流体と物体とで、Ｔの外法線方向が逆だからです。
物体は、変形しない微小物体になったので、質点とみなしてもいいでしょう。
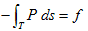
と定義します。ｆは、質点の位置のみに働く力です。従って、質点と流体を含む系の運動方程式は、4.(6)，(7)と今の結果より、
です。(F-1)のδはデルタ関数であり、質点の位置に特異点を持ちます。fにδがかかるのは、(F-1)を体積積分した時、質点の位置のみに働く力ｆになるものだからです。こうして並べてみると、なんとなくですが、1.(M-3)，(M-2)，(N-1)に似ていませんか？。
エネルギー保存則を導くために、(F-1)にｕをかけ、体積積分します。ｕをかけるのは、(F-1)の左辺が4.(5)より、
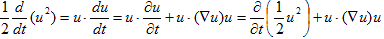
となるからです。 (F-1)より、
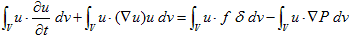(4)
が得られます。左辺1項目は、今やったように、
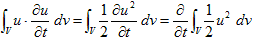(5)
です。右辺1項目は、デルタ関数の性質より、
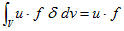(6)
です。右辺2項目は、
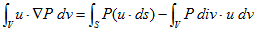(7)
となります。これは、5.(2)の部分積分版ですが、(F-2)より、div・u＝0なので、
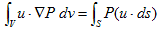(8)
です。(5)，(6)，(8)を(4)に代入し、5.でやったように、(4)の左辺2項目を移項すれば、
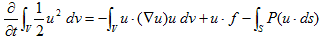(9)
が得られます。
(9)の左辺は、流体体積を1個の質点のように考えた時の、体積の持つ全運動エネルギーの時間変化を表しています。右辺2項目は、質点が流体に対して成した仕事（率）です。右辺3項目は、表面力が体積に対して成した仕事（率）です。何故なら圧力と速度の内積の形をしているからです。Ｐ(u・ds)＝u・Ｐｎ daです。圧力は、常にＳの内法線向きに大きさＰで働きます（−Ｐｎ daが、面積da上の圧力の合力）。右辺3項目しかない形を想像します。
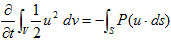
体積Ｖを1個の質点のように考えた時、その全エネルギーの時間変化は、その表面に作用した外力の成した、仕事に等しいと読めます。これはエネルギーの意味そのものです。さらに体積中に質点がなくても(9)は成り立ちます。u・f＝0となるだけです。そうすると(9)の右辺第1項は、表面力の仕事のようなものではないのか？、表面積分に直せるのではないか？、という気がしてきます。
次の関係式があります。tを転置として、
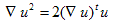(10)
(10)は成分で計算すれば一瞬です（微分形式を知ってれば、さらに良し！）。こんなにあからさまに書いてる本は少ないですが、(10)は、ベクトル解析の公式の一つと思って良いものです（実際、積の微分公式）。
(10)の両辺にｕ・をかけてみます。
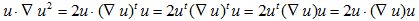(11)
ここでふっと、(7)を振り返ると(11)の最左辺は、(7)の左辺で、Ｐにu2を代入した形をしています。よって(11)と(7)より、
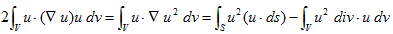
が得られます。再びdiv・u＝0より、
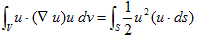(12)
です。これを用いれば(9)は、
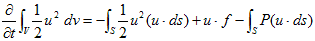(13)
となります。右辺1項目の意味は、もう言うまでもないと思います。
ところで今欲しいのは、質点と流体を含む系のエネルギー保存則です。つまり質点の運動エネルギーも考慮したいわけです。そう考えて(13)を見直すと、u・fは流体と質点の相互作用項なので、ｆは質点の運動方程式より、質点の速度で表せるはずです。実際(K-1)から、
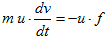(14)
が得られます。(14)でのuとｖの関係ですが、この質点はもともと、周囲でu＝一定とみなせるくらい小さな、変形しない微小物体として導入しました。物体は変形せず、その周囲の流速は場所によらず一定で、しかも流体は物体の動きに追随します。従って微小物体の質点極限では、u＝ｖとおけます。
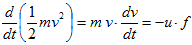(15)
(15)を(13)に代入し、移項すれば、
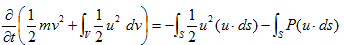(16)
となります。
(16)は、まだエネルギー保存則ではありません。後で言いますが、右辺が0になった時そうなります。右辺の積分は、積分体積の表面に関するものです。ただしこの体積は、任意に大きく出来ます。
流体が有限の広がりしか持たない場合、十分大きなＶをとれば、その表面Ｓに水はないので右辺のuは0とおけて、右辺は0です（ちょっと、ずるしてます）。
流体がどこまでも広がっている場合ですが（海のように）、これにはエネルギー保存則の成立条件を考える必要があります。エネルギー保存則は、孤立系に関して導けるものです。考えている系内の一部が、系外の何かと相互作用したら、系外から仕事が供給されるので、系のエネルギーは保存しないに決まっています。例えば太陽系は、隣りの恒星や遠方の銀河から微弱な重力しか受けていないと仮定し、それを無視する事によって初めて、太陽系全体のエネルギー保存則を導けます。
「系内の全ては、多くとも系内の全てとしか相互作用しない」が、孤立系の定義です。なので今は、流体と1個の質点だけを考えます。そうすると流体を動かす原因に成り得るものは、その1個の質点しかありません。
積分領域Ｖを無限に広く取れば、その表面（？）は、質点から十分遠いので、質点の影響は微小になり、そこでは静水状態が成り立っている、と考えるのが自然です。よってこの場合も、右辺のuは0で、右辺全体 も0です。
というわけで、
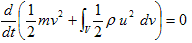(17)
です。(17)の左辺で、∂tをdtに直したのは、2項目の体積積分の結果は、時間のみの関数だからです。左辺1項目は、流体の運動方程式(F-1)における、質点との相互作用項ｆから生じたもので、生じるのは、流体が質点に対して成した仕事です。よって(17)左辺は仕事の受給関係を表し、その関係が時間的に不変である事が言えました。(17)が、質点と流体を含む系のエネルギー保存則です。
・・・久しぶりにやりましたが、けっこう大変ですね・・・。
７．まとめ
もう十分に長いので、今回はここでやめます。ただ、現時点で出せるだけの手がかりは、出したつもりです。荷電粒子と電磁場を含む系のエネルギー保存則の導出過程は、以下のように想像できます。荷電粒子−電磁場系の決定方程式と、質点−流体系の運動方程式が何となく似ている事に注目して、手順のアウトラインを考えます。
(1) Maxwell方程式を、荷電粒子へ仕事をするように変形する。つまり相互作用項を特定する。
(2) 荷電粒子を全て含む体積Ｖで、上記の変形を体積積分する。
(3) divを含む式を考え出す（ガウスの発散定理の部分積分版と思われる）。
(4) (3)を用いて、表面積分に直せるところは、全て直す。
(5) 相互作用項を、荷電粒子の運動方程式を利用して、荷電粒子の物理量で書き直す。
(6) エネルギー保存則の成立条件を考える。
(7) 得られた関係式が、仕事の受給関係になっている事を確認する。
(8) それが時間的に不変であれば、エネルギー保存則。
［参考文献］
[1]理論電磁気学，砂川重信，紀伊国屋書店，1999年．
砂川先生らしく、すごくオーソドックスに丁寧に、エネルギー保存則は荷電粒子の運動方程式から出発して、2.(4)以降を完遂します。
だけど一つだけ疑問があった。「荷電粒子の運動方程式」から出発して、なぜ、「電磁場を含む」エネルギー保存則を導けるのか？。こういう事ではないのか？、というのが前振りの2.になりました。
[2]ランダウ理論物理学教程2，場の古典論，ランダウ・リフシッツ，東京図書，1978年．
相対論の形成（みすず書房）で有名（？）な広重徹が訳者として名をつらねる。荷電粒子の運動方程式から出発して電磁場を含むエネルギー保存則を導けるなら、Maxwell方程式から出発して、荷電粒子を含むエネルギー保存則は導けないのか？。ランダウを開いてみたら、そうなっていた。しかもこちらの方が、見通しがいい。しかし行間を読まねばならぬのもランダウ。Maxwell方程式の変形過程の必然性を読まなければ、わかったとは言えない。
広重徹の相対論の形成では、Maxwell方程式の連続体力学的解釈がいかに破綻していったかを、ローレンツやケルビンの原論文に基づき、克明に跡付けていた。山本義隆の重力と力学的世界でもそうだった。力学的解釈は失敗したけれど、相対論によってとどめを刺されるまでは、それは最も有効な電磁場の扱い方でもあった。実際それで、光速問題を除き、電磁場のほとんどの問題は片付いていた。Poyntingがエネルギー保存則を導いた時も、同じ状況だったと思われる（確認はしてません）。
ここは連続体力学を参照すべきではないだろうか？。幸い前職の職業柄、弾性学と流体力学を少しは知っている。でも弾性学のTensor方程式は手がかかるのでやる気が起きないし、原稿にするには厄介すぎる。簡潔に、非圧縮性完全流体としよう。流体の運動方程式とMaxwell方程式が、思いのほか似ているので少し驚いた。質点−流体系のエネルギー保存則の導出過程を振り返ってみると、7.(1)〜(8)のようになりました。
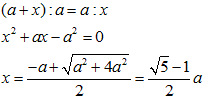
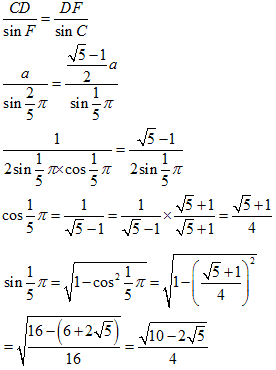
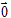です。
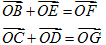
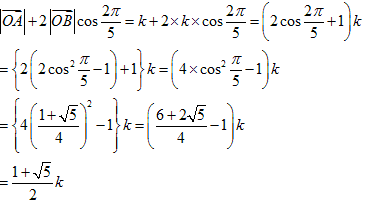
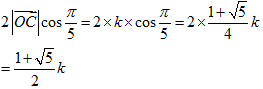
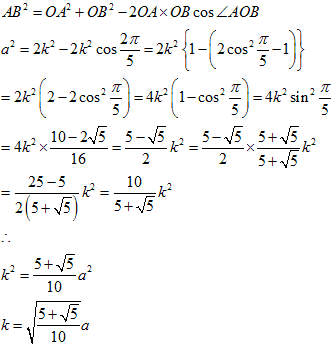
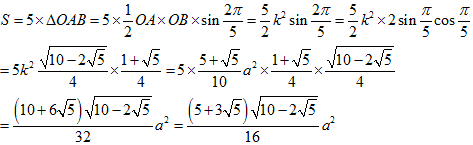
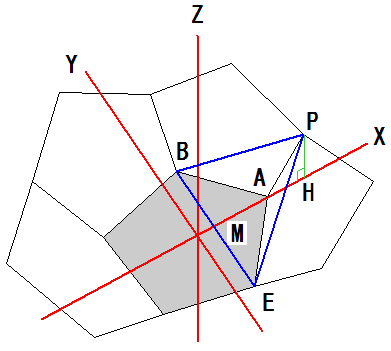
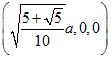
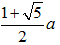なので、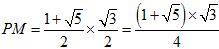
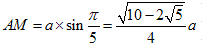
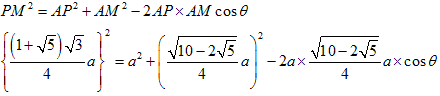
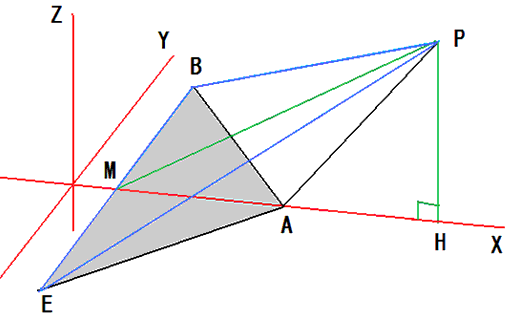両辺を16倍し、ａを約すと、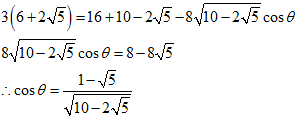
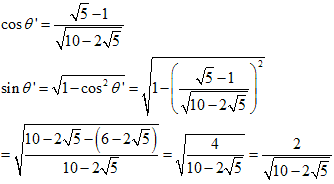
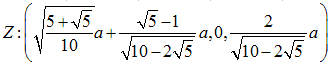
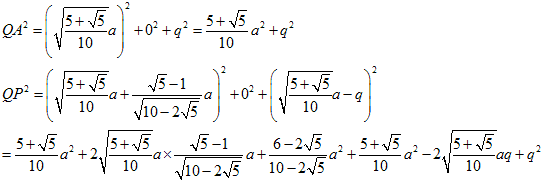
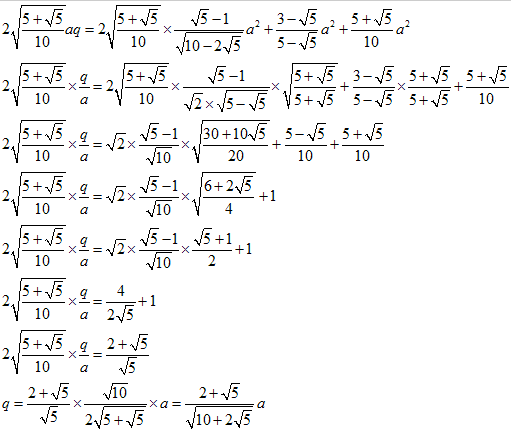
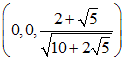
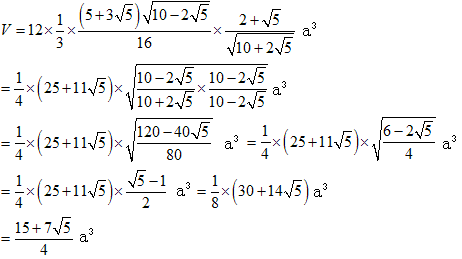
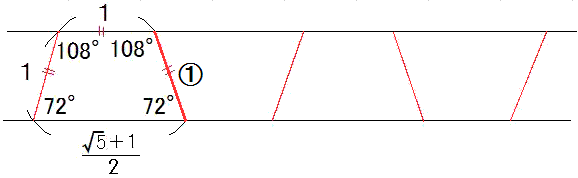
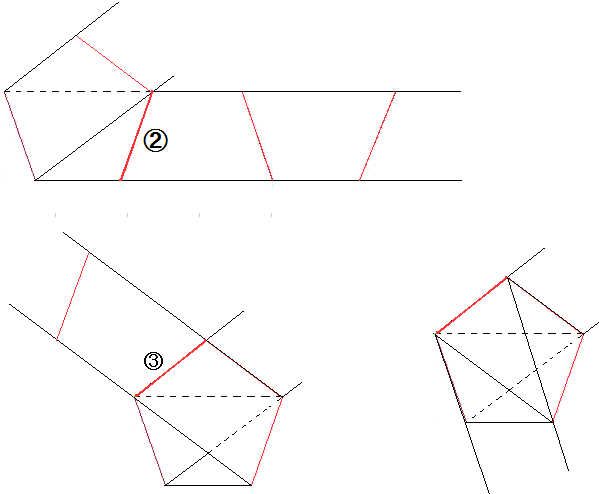
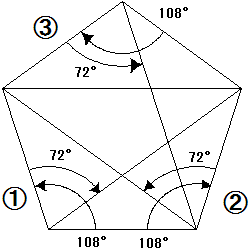
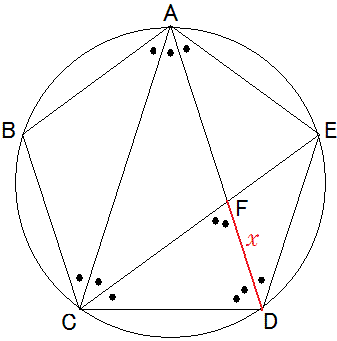
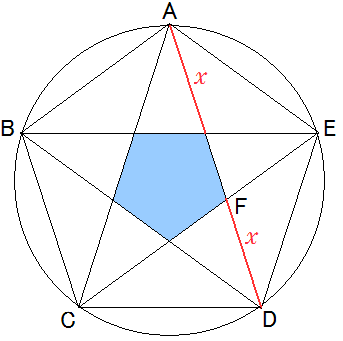
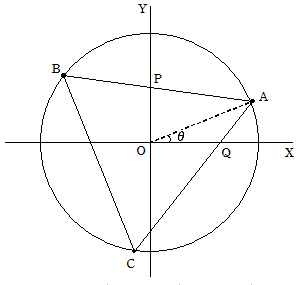図のように正三角形をＡＢＣとします。
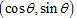とします。
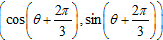です。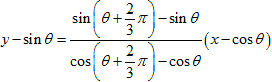
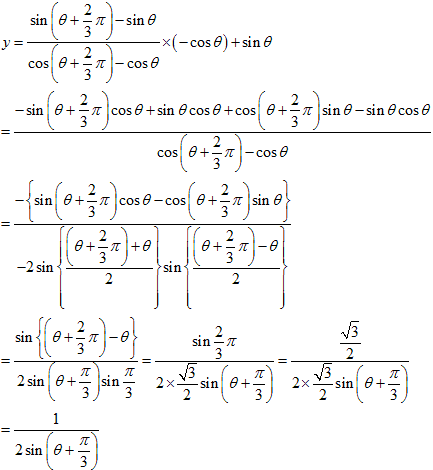
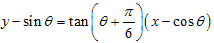
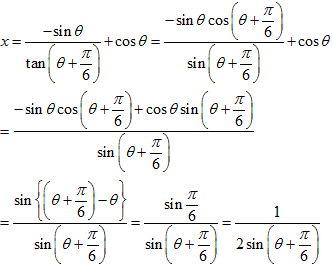
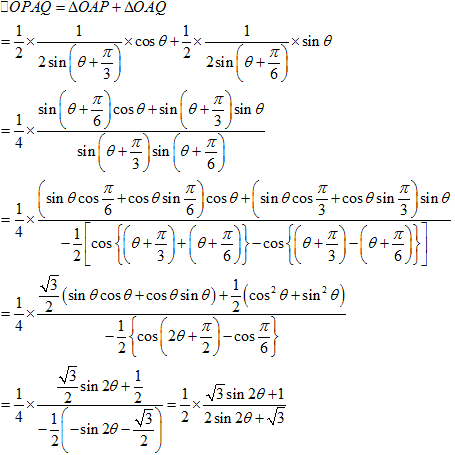
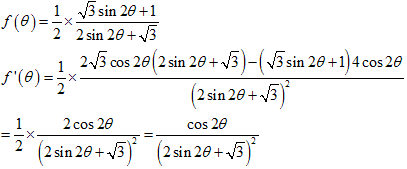
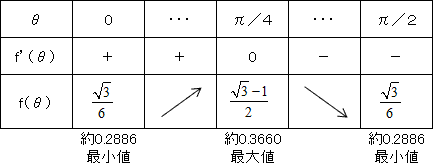
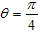のとき導関数が 0 になります。
