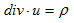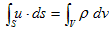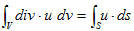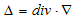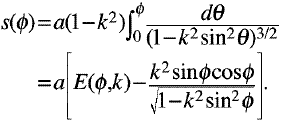NO.1748�@�@�@�A�C�[���X�^�C���O�p�`�@�@2008.10.26.�@�@���̗���
��Q�P�T�w�I�ȉ�����
�F����A���Z���w�ŏK���]���藝�������m�ł����B�O�p�`�̂R�ӂ̒�����a�A���A���Ƃ����Ƃ��ɐ��藧�藝�ł��B
���Q�����Q�{���Q�|�Q�����������Ƃ̂��Ƃł��B
�ӂ��ɑ���pC���P�Q�O���̂Ƃ��A ���Q�����Q�{���Q�{�����ƂȂ�B
�Ⴆ�Aa���R�A�����T�A�����V�������ł��B�ʖ����O�̎O�p�`�Ǝ��͌Ă�ł��܂��B
�ŋ߁A�u�����Ƃ����ڂ��v�i���{�]�_�ЁA�ꏼ�M���j��ǂ�ł�����A���̂悤�ȂR�ӂ̒����������ŁA�p���P�Q�O���ł���O�p�`���u�A�C�[���X�^�C���̎O�p�`�v�ƒm��܂����B
�����ŁA�������{���C�������i�܂��͂��j�C�������ł���O�p�`�͂��Q�����Q�{���Q�\���������A�p���U�O���ɂȂ�܂��B���ꂪ�����W�A�����T�A�����V�ƂȂ�A�ʖ��i�S���i���É��j�̎O�p�`�Ǝ��͌Ă�ł��܂��B
���āA���Q�����Q�{���Q�{�����������ł����A
a�����Q�|���Q�C�����Q�����{���Q�C�������Q�{�����{���Q�ƂȂ�܂��B
�������A���Ƃ��݂͌��ɑf�ŁA���|���͂R�̔{���Ȃ��B
��������A���ł��B
���P�F���A���Ɏ��R�������������ɑ�����āA�ia�A���A���A���{���j�g��������߂Ă��������B
���Q�Fa�����Q�|���Q�C�����Q�����{���Q�C�������Q�{�����{���Q�̂Ƃ��A���Q�����Q�{���Q�{���������Ă��邱�Ƃ��m���߂Ă��������B
���R�F�ς������i���{���j�͕K���W�S�O�̔{���ɂȂ邱�Ƃ��m���߂Ă��������B
���S�F�\�Ȃ�A���Q�����Q�{���Q�{�������������A
a�����Q�|���Q�C�����Q�����{���Q�C
�������Q�{�����{���Q�ƂȂ邱�Ƃ����߂Ă��������B
���F�A�C�[���X�^�C���i1823�`1852�j�̓h�C�c�̓V�ː��w�҂ł��B
���F���̋L���Ɋւ��铊�e�̌f�ڂ́A�Q�O�O�W�N11��17���ȍ~�Ƃ��܂��B
NO.1747�@�@�@�ȉ~�ϕ��ɂ��ā@�@�@2008.10.26.�@�@�O�p��K
�@
NO.1741�ɂ����āC�{���ӗ�����͂����炭���ׂĂ��������̏�ŏ����Ă�����̂ł͂Ȃ����C�Ɛ��@�v���܂����c
�@�e�_�y�э��W�C�p�Ƃ��E <�}1> �̂悤 �ɒ�߂�ƁC
�@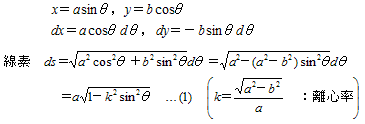
�ł�����C�ȉ~��̌� PR (������) �̒��� s ��
�@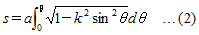
�ŗ^�����܂��B����̐ϕ��������C��2���(�s���S)�ȉ~�ϕ� E (k�C��) �ł��B
�@�悭�m���Ă���悤�ɁC���̐ϕ��͉�͓I�Ɏ��s���邱�Ƃ��ł��܂���B�����w���̍��́C���d�삪����i���l�j�̉ԁC���Ƀp�\�R���Ȃǂ���܂���ł����̂ŁCE (k�C��) ��ꐔ k �ɂ��ċ����W�J���C
�@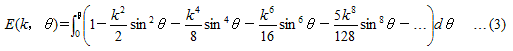
�Ƃ�����C�������x��(3)�Ɂu�����f���ϊ��v�Ƃ���ꐔ�̕ϊ����{���Ď����𑬂߂���Ƃ��낢��ȍH�v���������̂ł����B�ł����C�ߍ��ł́@�����x�v�Z�T�C�g�@�̂悤�Ȑ��l�v�Z�̂��߂̃T�C�g����y�ɗ��p�ł���悤�ɂȂ�C�u�̂̋�J�͉��������̂��I�v�Ɗ��S�ЂƂ����ł͂���܂��B
�@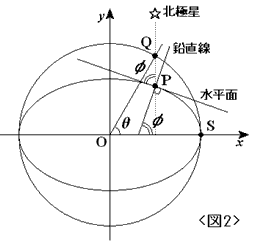
�@�Ƃ���ŁC�{�����������́C�ȉ~��̓_�ɂ�����@���� x ���ƂȂ��p�ӂ́C�� <�}2> �̑ȉ~��n���̒f�ʂƂ���Ƃ��C�V���ܓx �܂��� ���n�ܓx �Ƃ�����̂ł��B�}�� �� �͋��ʂ� �n�S�ܓx �Ƃ�
��C�ӂƂ̊Ԃɂ́C
�@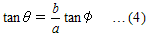
�̊W������܂��B�ł�����C�ԓ�S����ܓx�ӂ̒n�_P�܂ł̋��������߂�ɂ́C
<1> (4)����@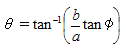 �@�ŃƂ����߂�B�@
�@�ŃƂ����߂�B�@
<2> �v�Z�T�C�g�𗘗p���@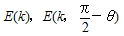 �@�����߂�B
�@�����߂�B
<3> 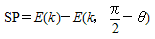
�Ƃ���̂������I���Ǝv���܂��B(2)���ӂɂ��Ă̐ϕ��ɕϊ����Ă��C �ŏI�I�ɂ͋����W�J�ɗ��炴��Ȃ��̂ł�����B
�@�b�͕ς��܂����C���̃j���[�g���́C�͊w�I�ȍl�@����u�n���͐ԓ������ɂӂ����]�ȉ~�́v�ƍl���C�����w�v�����L�s�A�x�̒��ŏq�ׂĂ��܂��B�����������ɂ́C(�V��)�ܓx��1���Ή�����q�ߐ��̒������C���ܓx�n���قǒ����Ȃ邱�Ƃ𑪗ʂŎ����悢�̂ł����C����͗e�ՂȂ��Ƃł͂Ȃ������悤�ł��B
�@�t�����X�́C1735�N����傪����Ȋϑ�����k�ɂɋ߂����v�����h�Ɛԓ��ɋ߂���A�����J�̃y���[�ɔh�����C�����ϑ������s���܂����B�����āC���8�N�̌�C�悤�₭�ܓx��1���ɑΉ�����q�ߐ��̒������O�҂̕����������Ƃ��m�F���C�j���[�g���̍l����������܂����B���̑��ʂ́C18���I�Ȋw�j��̈��s���ƌ����Ă��܂��B
NO.1746�@�@�Ɍ��l�́H(3) �@�@2008.10.26.�@�@�c�c�s
�Q�����A
�@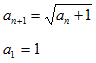
�̋Ɍ��l�́H�A�Ƃ������ŁA�u��ɗL�E�ȒP��������͎�������v�Ƃ����q���g���t���Ă��܂��B
�@�܂�{an}���P�������ɂȂ�an �͈̔͂����߂܂��Ban��0 �ɒ��ӂ��āA
�@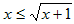
�Ƃ���A
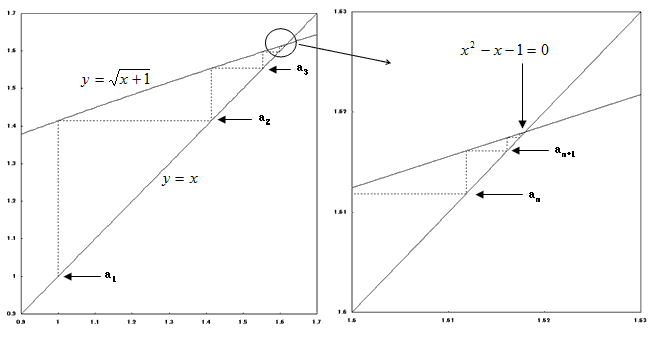
�@�@�@x2 - x - 1 �� 0�@�@�@(1)
�Ȃ̂ŁA
�@�@�@��2 - �� - 1 �� 0�@�@�@(2)
���A
�@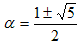
�ŁAan ���P�������ɂȂ�͈͂́A
�@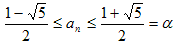
�Ƃ���D������2��51/2 �C(1�|51/2)/2��0�Ȃ̂ŁA
�@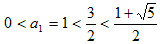
����Aa1��1 �͂��͈̔͂Ɋ܂܂�܂��B��������ƁA
�@�@�@1 ��an����
�ł���Aan �͒P�������ł��B�����ŁA�������ł�an ���P�������ŁA���A
�@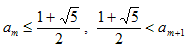
�ƂȂ�悤�Ȃ������݂���A�Ƃ��܂��B���̂悤��am �͈̔͂́A
�@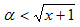
�łȂ���Ȃ�Ȃ��̂ŁA
�@��2 - 1 �� x
���A
�@��2 - 1 �� x ����
���K�v�ł��B�Ƃ��낪����(2)�����̂ŁA��2�|1���� �ł���A
�@�� �� x ����
�ƂȂ�̂ŁA���̂悤��am �͈̔͂͂���܂���B�]����an �̓����z���鎖�͂Ȃ��A
������̏�E�Ƃ��Ď��̂ŁAan �͏�ɗL�E�ȒP��������Ŏ������܂��B
�@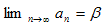
�Ƃ���A
�@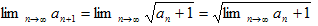 �@�@�i��̑o�A�������g���Ă��܂��j
�@�@�i��̑o�A�������g���Ă��܂��j
�Ȃ̂�
�@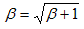
���Ȃ킿�A
�@�@�@��2 - �� - 1 = 0
�ł����A�܂��܂�(2)������āA
�@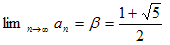
�������܂��B
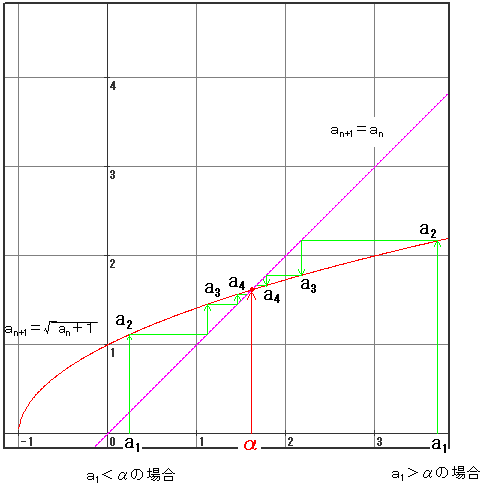
�@�Ƃ���ʼn��́A{an} ���P�������ɂȂ�͈͂��߂�(2)���A�Ɍ��l���߂�����ɂ��o�Ă���̂��H�A
�Ƃ����̂͋C�ɂȂ�Ƃ���ł��B�Ƃ���ł����A�}��`���Έ�ڗđR�ł��B
�@
�@���̐}�����Ă���ƁA{an} ���P�������ɂȂ�͈͂��߂�(2)���A�Ɍ��l���߂�����ɂ��Ȃ鎖�Ŗ{���I�Ȃ̂́A������`������A
�@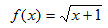
�ƁA����̍ċA�������`������A
�@�@�@g (x) = x
�̃O���t�̌`���Ƃ킩��܂��B����č���̖��́A���̂悤�Ɉ�ʉ��ł���Ǝv���܂��B
�m�藝�H�n
�@f�F�q���q���A
�@�@�@��2 = f (��2)�@�@�@(3)
�����āA��1��x����2 �͈̔́i��1����2�C��1���|���������j��f'(x)��0 �Ƃ���B
�@����ɁA
�@�@�@x �� f (x)�@�@�@(4)
�����藧�Ƃ���i���̏�����f(x)�́A��1��x����2 �͈̔͂�f(x)��x �̏�ɓʂȒP���������ɂȂ�j�B
�@����{an}n��1�C2�C�E�E�E �̏����la1���A��1��a1����2 �͈̔͂ɂƂ�A
�@�@�@an+1 = f (an)�@�@�@(5)
��{an} ���`����Ȃ�A
�@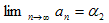 �@�@�@(6)
�@�@�@(6)
�����藧�B
�m�ؖ��n
�@��1��a1����2 �Ȃ̂�(4)�C(5)���A
��1��an����2 �͈̔͂ŁAan �͒P�������B
�����ŁA�������ł�an ���P�������ł��A
�@�@�@am����2 , ��2��am+1
�ƂȂ�悤�Ȃ������݂���Ɖ��肷��B���̂悤��x��am �͈̔͂́A
�@�@�@��2��f (x)
�łȂ���Ȃ�Ȃ��Bx����2 �Ƃ���Af'(x)��0�Ȃ̂�f ��x �Ő^�ɒP�������ŋt���������A
�@�@�@f-1(��2) �� x
��������B�]���āA
�@�@�@f-1(��2) �� x ����2
���K�v�B�Ƃ��낪��2 ��(3)�����Ax����2 �ł�f'(��2)��0 �Ȃ̂ł�͂�t��������A(3)���A
�@�@�@f-1(��2) = ��2�@�@�@(3)
�����藧�B�]���āA
�@�@��2 �� x ����2
�ƂȂ邪�A���̂悤��am �͈̔͂͂Ȃ��B�����an �̓�2 ���z���鎖�͂Ȃ��A
��2 ����̏�E�Ƃ��Ď��̂ŁA
an �͏�ɗL�E�ȒP��������Ŏ�������B
x��am����2 �̏ꍇ��(3)���A
�@�@am+1��f (am)
�ƂȂ��āA���炩�ɁA
�@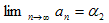
�����藧�B�����am����2 �̏ꍇ�ɁA��L�������B
�@am����2 �̏ꍇ�A�C�ӂ�an �Ń�1��an����2�B
����ĔC�ӂ�x��an ��f(x)��f'(x)��0 �ł���Ax��an �ŘA���ȒP���������Ȃ̂ŋt���������A�t�����A���B�]����f ��x��an �őo�A���i�����j�Ȃ̂ŁA
�@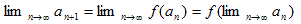
limn���� an ����������Ȃ�A��L�����藧�Blimn���� an �̎����́A
��Ŏ������B
�@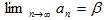
�Ƃ���A
�@�@����f (��)
�ƂȂ�Ban �̓�1��an����2 �ł��邩��Aan �́A��1��������2 �ȊO�̃��ɂ͎����ł��Ȃ��B�]����(3)���A
�@�@������2
���K�v�ŁA
�@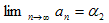
��������B
�m�ؖ��I�n
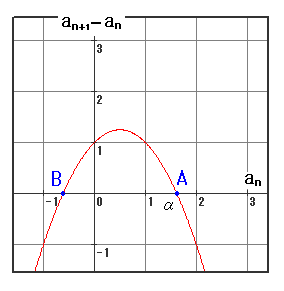
�@��L�ؖ����������Ƃ��Ăł����A���̐}�����āA�e�Y����͂ŕW���I�ɗp������A�C���j���[�g���E���v�\���@�̍�������ȁA���Ďv���܂����B���ɂȂ�܂����E�E�E�B
�@�}-1�͒e�Y����͂ɂ�����j���[�g���@�̊T���}�ŁA�}-2�́A�C���j���[�g���E���v�\���@�̊T���}�ł��B�O�̐}�Ɨǂ����Ă��܂��B
�@��L�ؖ��ɂ����āAf(x)���P�������ł��鎖�͖{���I�ł��B���̏������O���Ɓu�ǂ��炢�ځv�ɉ�܂��B�}-3�́A�c�ݓ���N������f(x)�Ɂi���́|�c�Ȑ��Ɂj�P�������Ȃ��Ȃ����ꍇ�ł��B���̏ꍇ�́A����2�ɂȂ�́A�����o�H�����邮�����Ĉ��肵�Ȃ��͂ŁA�����ł�낤�Ƃ���Ɓu�����҂ǂ��ځv�ɉ�܂��B
�@�����ʼn�̓\�t�g���g���킯�ł����A�����X�e�b�v��v�Z���@�A�����p�����[�^�̗^�����ɂ���āA�Ȃ��Ȃ����������Ă���܂���B���́u�d�q�v�Z�@�S���̎���v�ɁA�u���ƌo������������v�Ƃ����A�Ȃ��Ȃ��g�z�z�Ȏ��ԂɊ������܂�܂��B�ł������͏o���Ȃ��ƁA�����o�Ȃ����E�E�E�B
NO.1745�@�@�Ɍ��l�́H(2) �@�@2008.10.26.�@�@��ӂ����̂炢��������
�� ����o��n�p�̊e���̒l�͐��ł��邱��
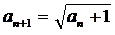
�Q�����̐��藧������A���̐���̑�Q���ȍ~�̒l�͐��ł��B
�i���̕��������Ƃ��Ă���j
 �� �K���ɂ���
�� �K���ɂ���
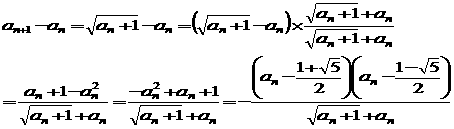
�E�̃O���t���A 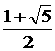 �@�@���召�̋��ڂɂȂ�܂��B
�i�_�`��X���W�A���̒l�����Ƃ���j�܂�A
�@�@���召�̋��ڂɂȂ�܂��B
�i�_�`��X���W�A���̒l�����Ƃ���j�܂�A
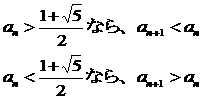
�� ����o��n�p���P���ŗL�E�ł��邱��
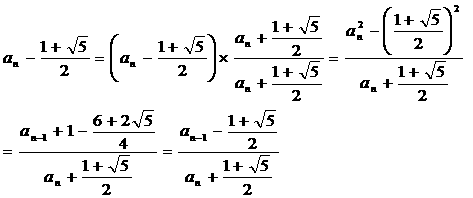
��������̂悤�ɗ��L���܂��B
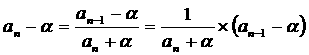
���̎��ɂ��āA���q�̂Ȃ��̕������u�{�v�ł�����̂q�E����Ɏ��X�Ƃ����Q������p���ĕό`���Ă����A
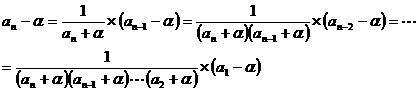
���̎��̕���́A���ł��B
k��1,2,3,4,���,n-1 �Ƃ��܂��B
����ƁA���̌��ʂ́A��n�|���Ƃ�k�|���Ƃ��������ł��邱�Ƃ������Ă��܂��B
�܂�A����o��n�p�̊e���̒l�́A����肷�ׂđ傫�����A���������ƂȂ�܂��B
������A���̌��ʂƊK���̌��ʂ����킹��ƁA����o��n�p���P���ł��邱�Ƃ�������܂��B
�܂�A��1�����Ȃ�P�������A��1�����Ȃ�P�������ƂȂ�܂��B
��1�����̂Ƃ��A���̐���͒P�������ł��B
���̂Ƃ��A��1�|�����O�ł��B
�P�������Ȃ̂ɁA��n�|���̕��������̂܂܂ł��邱�Ƃ́A
�o��n�p�����ɗL�E�ł��邱�Ƃ������Ă��܂��B
��1�����̂Ƃ��A���̐���͒P�������ł��B
���̂Ƃ��A��1�|�����O�ł��B
�P�������Ȃ̂ɁA��n�|���̕��������̂܂܂ł��邱�Ƃ́A
�o��n�p����ɗL�E�ł��邱�Ƃ������Ă��܂��B
�� ��������l�̂���
���̊W���l�����܂��B
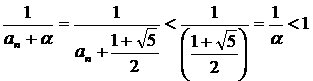
����ƁA
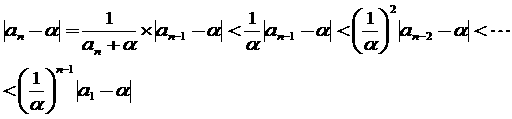
���̎��ŁA�������Ƃ���ƁA �@�@�Ȃ̂ŁA
�@�@�Ȃ̂ŁA
��n�́A���Ɏ������܂��B
���́A��1���P�ł����A�����̒l�ɂ�����炸�A ���̐���o��n�p�́A���Ɏ������܂��B
�� ���ʂ����o���ꍇ
�������邱�Ƃ�O��ɂ���A�����傫�ȂƂ��́A��n����n-1�������Ȃ��Ȃ�A
���̕������̉��������l�ƂȂ�܂��B
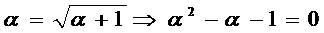 �@�@�@�i�������A���̉��j
�@�@�@�i�������A���̉��j
�� �����̗l�q�����o�I�Ɍ���ꍇ
NO.1744�@�@�x�N�g�����Minimum(1) �@�@2008.10.26.�@�c�c�s
�@�ŋ߂悤����ƁA�d���C�w�������{�C�ŕ�����C�ɂȂ�܂����B�E�E�E���āA���܂Œm�������Ԃ肵�ĐF�X�����Ă��������ɁA�{�C����Ȃ������̂���I�E�E�E�Ƃ������ȓ˂����݂́A������������Ă����܂��B����͂ƌ����A�܂��A��w�̋��{����Ɏ���������ƁA�d���C�ɂ��W����v�Z�����Ă��������ɁA�Ȃ�Ƃȁ`���A�ȒP�Ȗ�肭�炢�Ȃ�v�Z�ł���悤�ɂȂ����A�Ƃ������x�ł��B
�@�{�i�I�ȓd���C�w�̖{���āA�Ȃ��Ȃ��ǂދC�ɂȂ�Ȃ���ł���ˁB��\�I�ȂƂ���ł́A�g�����X����o�Ă���W���N�\���̓d���C�w�i�㉺�j������܂����A9800�~�~2�i700�y�[�W�~2�j�Ȃ�Ă̂���������ƁA���Ȃ���C���킪��܂��B�Ƃ͌������̂́A�����Ƃ������肵���{��I��ŁA����Ȃ�ɖ{�C�œǂ�ł݂�ƁA�d���C�w���Ċ�{�����Ɍ����ĂȂ�A���̂������R���p�N�g�ɂ܂Ƃ܂�̂��킩��܂��B�Ⴆ�ΐÓd���ۂȂ�āA�{���Ɋ�{���������Ȃ琔�y�[�W�ōς݂܂��B�����Ŏ��K�m�[�g�̈�Ƃ��āA�x�N�g�����Minimum�C�d���C�wMinimum�Ƃ����̂��A����Ɋ�悵�܂����B
�@�d���C�w�́A�͊w�ȏ�ɏ��S�҂ɑ���~���������ƌ����܂����A����̓x�N�g����͂̒m�����Ȃ��ƁA�����v�Z���T�������Ă��傤���Ȃ����炾�Ǝv���܂��B�܂����_�`�����������肳���邽�߂ɂ́A�f���^���̈������K�v�ł��B�����͊���Ă��܂��ΒP�Ȃ�v�Z����Ƃ��Ĕ[�����ł��܂����A�ŏ��͂���ς�A�S�R�C���[�W�������Ȃ��āA���ʂ��������Ȃ��ē�c���܂��B�Ƃ����킯�ŁA�ŏ��Ƀx�N�g����͂ƃf���^���̃C���[�W�������܂��B
�P�D�ށi���z�j�D
�Q�D�|�e���V�����D
�R�D���ʕۑ����D
�S�Ddiv�i���U�j��Gauss�̔��U�藝�C���i���v���V�A���j�D
�T�D���i�f���^���j�ƃ��v���X�������̊�{���D
�U�D�Δ����̏���������rot�C�ۑ���C�ϕ��L�����̔����D
���̌�ŁA�d���C�wMinimum(1)
�Ƃ��������ł��B
�P�D�ށi���z�j
�@3������Ԃ̓_(x�Cy�Cz) ��Ɨ��ϐ��Ƃ������(x�Cy�Cz) ���l���܂��B��(x�Cy�Cz) ���̂͂��鐔�l�i�X�J���[���j�Ƃ��܂��B�ނ̓i�u���Ɠǂ݂܂����Agrad�Ə�����鎞������܂��B���{���ł͌��z�ł��i�p���gradiant�j�B
�@�ނƂ́A��(x�Cy�Cz) �̔������J�b�R�ǂ��x�N�g���`���ɂ܂Ƃ߂������̘b�ł��B�Ƃ肦��1�ϐ���(x)�ōl���܂��By����(x)�̔����͂悭�A
�@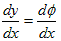
�Ə�����܂����A�����Ɍ����ƁA����͔����ł͂Ȃ������W���ł��B���̓_�ł̐ڐ��̌X����\���܂��B�����W���̒�`�ɖ߂�A
�@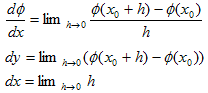
�Ƃ����C���[�W�ł��B
�@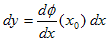 �@�@�@(1)
�@�@�@(1)
������(x)�̔����ł��B(dx�Cdy)�Ƃ́A(h�C��(x0�{h)�|��(x0))�̋Ɍ��ŁAh��(x0�{h)�|x0 �ł��鎖����A���ꂪ�A���̈�_(x0�C��(x0))����̔����Ȋ��̑�����\���͖̂��炩�Ǝv���܂��B(1)�́A�����ȑ���dx�Ɋւ��ẮA��(x)�͈ꎟ���ɂȂ��Ă���ƌ����Ă��܂��B���̈ꎟ���̌X�����A
�@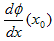
�ł��B���̃C���[�W�͖c��܂������o���܂��B(1)��(dx�Cdy)������Ƃ����A�������ɉ������Ă�����ꍇ�Ay0����(x0)�Ƃ��āA����(dx�Cdy)�́A(x�|x0�Cy�|y0)�Ə����܂��B���̎�(1)�́A
�@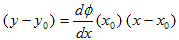 �@�@�@(2)
�@�@�@(2)
�ƂȂ�A���̈�_(x0�Cy0)�ɂ�����ڐ��ɂȂ�܂��B�ڐ��Ƃ͊��̈�_��ڂɌ�����悤�Ɋg�債�����̂ł���A�t�ɐڐ�������Ȃ�i�����\�Ȃ�j�A���̈�_�ɂ͔����Ȑڐ�(2)�����ߍ��܂�Ă���ƍl���Ă��ǂ��ƁA(1)�͌����Ă��܂��B���̃C���[�W������ɏ����A
�@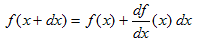 �@�@�@(3)
�@�@�@(3)
�Ƃ������ɂȂ�܂��B�ꎟ���Ȃ�(3)�́A������̔C�ӂ̓_�Ŗ������ɐ��藧���܂��B
(3)�̃C���[�W�Ń�(x�Cy�Cz) �̔����������܂��B��(x�Cy�Cz) �̔����̖ړI����ϐ��̏ꍇ�Ɠ����ł��B�Ǐ��I�Ɋ����ꎟ�����i���`���j���鎖�ł��B(dx�Cdy�Cdz) ���������Ƃ��āA�����A
�@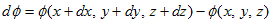 �@�@�@(4)
�@�@�@(4)
���l���܂��B��ϐ��̏ꍇ�Ɠ����悤�ɁA(4)���܂�x�ɂ��Đ��`�����܂��B
�@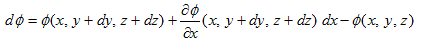
�ƂȂ�͖̂��炩�Ǝv���܂��i��ϐ��̏ꍇ�Ɠ����ł��j�B�����ʼn��́A�Δ����݃�/��x���ƌ����ƁA
�@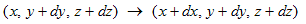
�ƁAx�������ω������ƍl���Ă��邩��ł��B���Ƀ�(x�Cy�{dy�Cz�{dz)��y�ɂ��Ă����������ł��܂��B
�@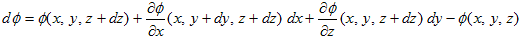
���x�́A
�@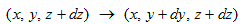
�ƍl���Ă��鎖�ɂȂ�܂��Bz�ɂ��Ă������ł��B
�@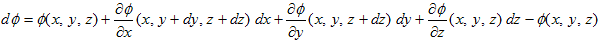
�ƂȂ�A
�@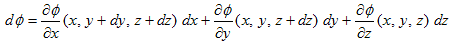 �@�@�@(5)
�@�@�@(5)
�������܂��B(dx�Cdy�Cdz) �������Ȏ����l�����āA(dx�Cdy�Cdz)��(0�C0�C0) �̋Ɍ��ōl����Ɓi������Ƃ��邢�ł����ǁj�A
�@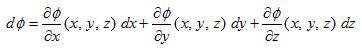
�Ȃ̂ŁA������ȗ����āA
�@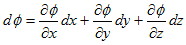 �@�@�@(6)
�@�@�@(6)
�Ə����A�S�����ƌĂт܂��B�Ӗ��͔����Ɠ����ł��B������(5)�ɂ����āA(dx�Cdy�Cdz)��(0�C0�C0) �̋Ɍ�����鎞�A(x�Cy�{dy�Cz�{dz) ��dy��dz��0�ɂ��邭���ɁA�Ȃ�Ł݃�/��x�ɂ�����dx�Ȃ�0�ɂ��Ȃ��H�A�Ƃ����^��͎��ɓ��R���Ǝv���܂��i���������邢���ł��j�B
�@���͂����ɂ́A�udx�Cdy�Cdz�Ȃǂ̔����v�f�͎c�������I�v�Ƃ����ړI�ӎ��������Ă��܂��B�Ƃ����̂́Adx�Cdy�Cdz���c���Ă����ƁA�����I�Ȍv�Z���s���邩��ł��B
���炩�ȗ�Ƃ��āA����̐ϒ��u�̎��ʂ��ƁA���̖��x�ςƂ̊W�������܂��B
�@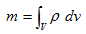 �@�@�@(7)
�@�@�@(7)
(7)�́A�Ӗ����l����Ζ��炩�Ȏ��ł����A�u�Ӗ����l���Ȃ���Ȃ�Ȃ��v�Ƃ����Ƃ��낪�|�C���g�ł��B����A�����̐�dv �̔�������dm �́A
�@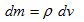 �@�@�@(8-1)
�@�@�@(8-1)
�Ȃ���i���x�~�̐ρj�A�S���ʂ��́A�����̍��v�ŁA
�@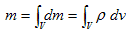 �@�@�@(8-2)
�@�@�@(8-2)
�ƂȂ�Ɍ��܂��Ă�A�Ƃ����l�����ł��܂��B���̗�ł͋͂��ȍ������m��܂��A(7)�̈Ӗ��������Ȃ�l������A(8-1)��(8-2) �Ƌ@�B�I�Ɍv�Z��������A�T�O�Ƃ��ėy���ɈՂ����Ƃ͎v���܂��H�B�����ƕ��G�ȃP�[�X�ł́A�����v�f�������炳�܂Ɏc���Ă����Ȃ��ƁA�Ӗ������ނ̂ɔ��ɓ�V����ꍇ�����肦�܂��B���̂��߂�(6)�ł��Adx�Cdy�Cdz���c���܂��B������(7)���疾�炩�Ȃ悤�ɁA�Ō�̌��_���ɂ܂ŁA�����v�fdv ���c��͕̂s�ł��B
�@�����Ŕ����v�f�����ƁA�Ō�̌��_�ɂ܂Ŏ����z���ėǂ������Ƃ��A�ŏ����番���Ă����܂��B(6)�́A
�@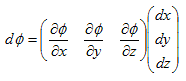 �@�@�@(9)
�@�@�@(9)
�Ə����܂��B�����ł́A���x�N�g���Əc�x�N�g�������̏��ɕ��ׂ����̂��A�x�N�g���̓��ς�\�����̂��ƁA���܂��i���������ォ��A���ϋL���E���g���܂��j�B
�@(9)�̉��x�N�g���Əc�x�N�g�����A
�@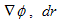
�Ə������ɂ���A
�@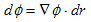 �@�@�@(10)
�@�@�@(10)
�ƂȂ��āA�����v�f�����Ƃ����łȂ������m�ɕ����ł��܂��B���̂��߂ɂ́A�x�N�g���L�@�̓������K�v�ł����B���ꂪ�x�N�g����͂��g�����R�̈�ł��B
�@�@1���x�N�g���L�@�ɂ���āA�����v�f�����Ƃ����łȂ������Ƃ�����D
�@�Ƃ��낪(10)�ɂ́A�����ƈӖ���t�^����]�n������܂��B�ގ��̂��`���I�ɁA
�@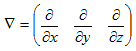
�Ƃ����x�N�g���i�x�N�g����p�f�ƌĂт܂��j���ƒ�`����ƁA�ރӂƂ́A�x�N�g��������X�J���[�ŁA
�@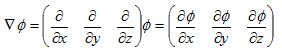
�Ə�����̂ŁA(10)�̓x�N�g��������X�J���[�̃x�N�g���ރӂƁA�x�N�g��dr�Ƃ̓��ςȂ̂ŁA���ʂ͂���X�J���[ d�� �ɂȂ�ƁA��u�œǂ߂�悤�ɂȂ�܂��i����Ă���ł����j�B�x�N�g����͂��g����ڂ̗��R���A���̃J�b�R�ǂ��ł��B
�@�@�Q���x�N�g���L�@�ɂ���āA���G�Ȏ��̔��ǂ��e�ՂɂȂ�D
�@�Ƃ����
�@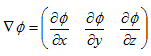
�ɂ́A��(x�Cy�Cz) �����̊e�_�ŁA�ǂꂾ���}�s�ɕω����邩�i�ǂꂾ���X���Ă��邩�j�̏�S�Ċ܂܂�Ă��܂��B��������́A�����W���ł�����B���������킯�ŁA�ނ͌��z�ƌĂ�܂��i1�����Ȃ�X���j�B
�Q�D�|�e���V����
�@��Ƃ��ẮA��͂藬�̗͊w�i���̗���j���킩��₷���Ǝv���܂��B���̗͊w�ɂ����Ă��悻�m�肽�����Ƃ́A�e����t�ɂ������Ԃ̊e�_(x�Cy�Cz) �ł̗����i����̑����j�Au��(vx�Cvy�Cvz) �ł��B���ꂳ���킩��A���̈��͂���g�̌`�ɂ�����܂ŁA�����I�ɂ͑S�Čv�Z�\�ł��B�ŁA���̉^���������́E�E�E�A
�@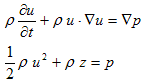 �@�@�@(1)
�@�@�@(1)
�Ȃ�Ď��ɂȂ�܂��B�ς͗��̖̂��x�ŁAp�͈��͂ł��B����ɂ��x�N�g����͂��g���Ă��܂����A������ɂ��Ă����������Ȃ����ł��鎖�ɂ́A�ς�肠��܂���B����(1)�𐬕��ŏ��������A(vx�Cvy�Cvz�Cp) ��4�ϐ��̘A���Δ����������ɂȂ�܂��i�������Ȃ��A�������Ȃ��E�E�E�j�B
�@���̗͊w�ōŏ��ɔ��W��������́A�k���Q�Ȃ����S���̂ƌĂ��̈�ł����B����ɂ͗��R������܂��B���x�|�e���V�����ӂ̑��݂����炩�ɂȂ�������ł��B���x�|�e���V�����ӂƂ́A
�@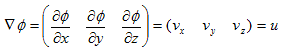 �@�@�@(2)
�@�@�@(2)
�Ƃ������̂ł��B(1)�ł́A4�ϐ��A���Δ����������ł��������̂��A���x�|�e���V�����ӂ̓����ɂ��A��������̃X�J���[�������߂���ɋA���ł��܂��B���������̎x�z�����������A(1)�ɔ�ׂ�A
�@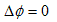
�Ƃ����A�������Ȃ����炢���₷�����̂ł����i���ɂ��Ă͌�q���܂��j�B
�@��ʂ�(2)�̌`�ŁA���߂����x�N�g���l��^���Ă����X�J���[�����A�|�e���V�����ƌ����܂��i���Ȃ萔�w���̒�`�ł��j�B���߂����x�N�g���l�ɑ��ă|�e���V���������݂���ƁA�v�Z���i�i�Ɋy�ɂȂ�܂��B
�@�܂��|�e���V�����͂ӂ��A���炩�̕ۑ����ƊW������܂��B�����ł́A�ۑ����ɂ���ė��_�̑唼�ȏオ���܂����肵�܂��B�Ȃ̂ŁA�ۑ����ɊW�����|�e���V�����͂ǂ��ǂ��������A�v�Z�̑唼���y�ɍς܂����A�ƂȂ�͕̂K��ł��B�|�e���V�����͑�Ϗd���܂��B
�R�D���ʕۑ���
�@�Ăї��̗͊w���������܂��B
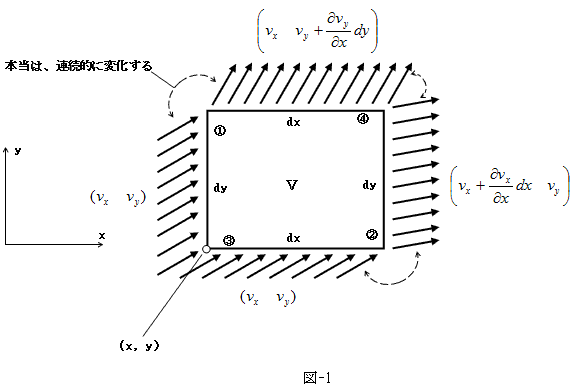
�@2�����ň���������Ɉ�l�ɐ�������A���̕�����x����������Ƃ��܂��Bx���ɕ��s�ɒ����`�u�i�̐ςu�j���Ƃ�܂��B�܂�����������̈�l�ȗ�����u�i�X�J���[�j�Ƃ��܂��B
�@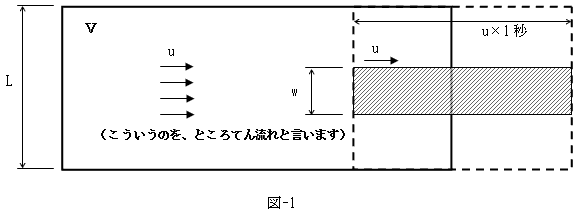
�@�}-1�Ɏ������悤�ȗ�����A��l�������ƌ����܂����A������u�Ƃ���Ă�v�Ə̂��l�����܂��B�Ƃ���Ă�ɂ���āA�̐ςu����1�b�Ԃɗ���o�����ʂ��l���܂��B�c�ӂ̒�����L(m)���Ƃ���ƁA����͓_���ň͂����ʐςɂȂ�܂����A���̈ꕔ�̕��������o���Ă݂�ƁA
�@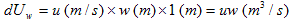
�ł��B�Ō�� �~1(m) �́A���s��1(m) �ōl���Ă�Ƃ������ł��B��l�������Ȃ̂ŏc��L��ŁA��������̗���o���̋��x�i���x�j�́AL��̏ꏊ�ɂ�炸���̂͂��ł��B
�@�]���āA�̐ςu����1�b�Ԃɗ���o�����ʑ��x�́A
�@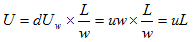
�ƌv�Z�ł��܂��B���ɑ̐ςu�ɑ��āA���ꂪ�ƌX���Ă���ꍇ�͂ǂ��ł��傤�H�B
�@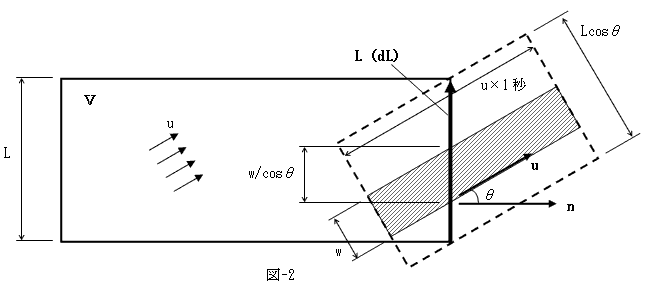
�@�}-1�Ɛ}-2�̃n�b�`��������ӂ̒������ׂ�킩��悤�ɁA�������o�ʐρi�̐ρj��u�ɑ��āA���o�����i�f�ʐρj�́A1/cos�Ɣ{�ɑ����Ă��鎖���킩��܂��B����͒P�ʒ����i�P�ʒf�ʐρj������̗��o���x�i���x�j��cos�Ɣ{�Ɍ����������Ӗ����܂��B1�b�Ԃ̗��o������cos�Ɣ{�Ɍ���͂��ł��B���ہA�}-2�̓_�����̏c�ӂ̒����́ALcos�Ƃł��B����Ă��̏ꍇ�ɁA�c��L��ʂ���1�b�Ԃɂu���痬��o�����ʂ́A
�@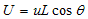
�ƂȂ�܂��B�Ƃ����L�͔C�ӂɏ������Ƃ�܂��BL�������ȏꍇ���l���A�����dL�ŏ������Ƃɂ��܂��B
�@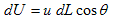
�@����ɁA
�@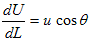 �@�@�@(1)
�@�@�@(1)
�ƕό`���Ă݂�ƁAu cos�Ƃ͍��ӂ̈Ӗ�����AdL���痬��o�����ʂ́A���o���x�i���x�j�ł��鎖���킩��܂��B�Ƃ���ŃƂƂ́A��l����u�Əc��dL�̐����p�ł��Bu��dL���x�N�g���ƍl���AdL�ɁiL�Ɂj�E���ɒ��s����P�ʃx�N�g��n ������A(1)�́A
�@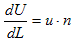
�Ə����܂��B�Ă�dL���E�ӂɈڍ�����ƁA
�@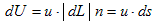
�ƂȂ�܂��B
�@|dL|n����f�x�N�g���ƌĂсAds�ŕ\�킷�̂����킵�ł��Bd�t�́A�����Ȓ���dL���痬��o���A�P�ʎ��ԓ�����̗��ʂ��ƍl�����܂��B3�����̏ꍇ�́A2�����̂Ƃ�|dL|���A�����Ȓ����i�Ȑ��j�̒�����\�킷�̂ɑΉ����āA�����ȕ��ʁi�Ȗʁj�̖ʐς�\�킷�̂ŁAds�͖ʑf�x�N�g���ƌĂ�܂��Bds�́A2�����ł�3�����ł��A�l���Ă���ʐς�̐ς̊O�@�������Ɏ���Ȃ��ƁA�ȏ�̋c�_�͐��藧���Ȃ����͒��ӂ��܂��B���@���������ƁA���o�������ɂȂ��Ă��܂�����ł��B
�@�����ŔC�ӂ̋Ȑ���Ȗʂ́A�����̍l����p���Đ��`������A�Ǐ��I�ɂ͔���������������ʂƍl�����鎖�ɒ��ӂ��܂��B�]���āA
�@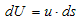 �@�@�@(2)
�@�@�@(2)
�́A�C�ӂ̋Ȑ���Ȗʂ̊e�_�Ő��藧���Ă����\�킵�������ƌ����܂��B
�@�ȏ���(2)������A�C�ӂ̕Ȑ��ň͂܂ꂽ�ʐς�A�C�ӂ̕Ȗʂň͂܂ꂽ�̐ς��痬��o���A�C�ӂ̗���ɑ��闬�ʑ��x��\�킷���́A�e�Ղɓ����܂��B����ɂ́A�P�D��(8-1)��(8-2)�̉ߒ��Ŏg�������ʂƖ��x�̊W�Ɋւ���A�@�B�I�Ȍv�Z�菇���v���o�������ŏ\���ł��B���炩�ɁA
�@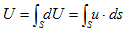 �@�@�@(3)
�@�@�@(3)
�ƂȂ�܂��B�����łr�́A���ʑ��x�t���l���Ă���C�ӂ̕Ȑ���Ȗʂł��B
�@(3)�́A����̐ςu���͂ޕȖʂr���痬��o�����ʑ��x��\���Ă��܂��B���܂ŗ���o���ƌ����Ă��܂������Au�ds�͕����������Ă���̂ŁA�ꏊ�ɂ���ė��o�������藬���������肵�܂��B
�@(3)�́A����������Ȗʏ�ō��v�������̂ł�����A�t�͑̐ςu����̗��o�C�̐ςu�ւ̗����̎��x��\���Ă��܂��B
�@�̐ςu�͈��ł��B�]���āA���͂u�ɓ������������A�o�čs���Ȃ���Ȃ�܂���i���͈��k����Ȃ��j�B����Ēʏ�́A
�@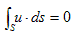 �@�@�@(4)
�@�@�@(4)
�ł��B�����A
�@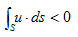
�Ȃ�A�u�̂ǂ����Ő��͋z�����܂�Ă��鎖�ɂȂ�܂��B�܂��A
�@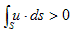
�Ȃ�A�u�̂ǂ����Ɏ����t���Ă��āA�������琅�͗N���Ă鎖�ɂȂ�܂��B�N���o���i���j�̕�����ς���z�����݂ɂ��Ȃ�̂ŁA�Ȍ�͗N���o���̂ݍl���܂��B
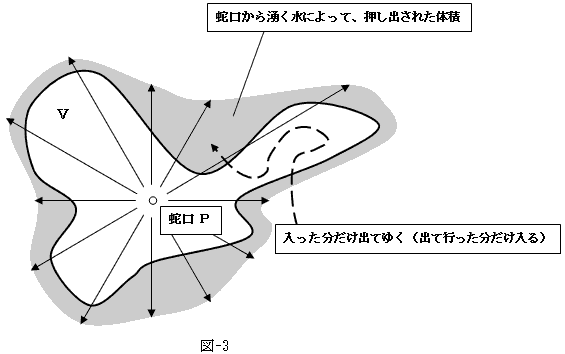
�@�}-3�̏�Ԃ��l���܂��B������N�������́A���Ƃ���u�ɂ��������������o���̂ŁA�K���N�������������o�������܂��B
�@����A�O������̗������������R�ŁA�������������u���łǂ�Ȍo�H�𗬂�悤�ƁA�������������o�čs���܂��i�v�����(4)�ł��B�t�Ɍ����A�o�čs���������������ė���j�B
�@����Ď�����̗N���o�����x�����Ƃ����ꍇ�A
�@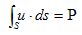
�ɂȂ�ƌ��_�ł��܂��B
�@�܂��A�N���o�����������Ă��A���ǂ͑̐ς̎��x�ŁA����͈��i�u�j�łȂ���Ȃ�Ȃ��̂ŁA
�@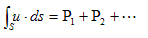
�ł��B
�@
�@����Ƀ����A���I�ɕ��z���Ă���ꍇ���l�����܂��B���̏ꍇ�́A���łȂ��A�N���o�����x�ς��g���ׂ��ł��A�����̐ς���̗N���o���ʂ͕b������A
�@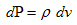 �@�@�@(5)
�@�@�@(5)
�ɈႢ�Ȃ�����i1.(8-1)�Ɠ����j�A�S�̂Ƃ��ẮA
�@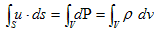 �@�@�@(6)
�@�@�@(6)
�ɈႢ�Ȃ��ƂȂ�܂��i1.(8-2)�Ɠ����j�B����(6)�́A�N���o��������ꍇ�̗��ʂ̎��x��\���Ă���̂ŁA���ʕۑ����ƌĂ�܂��B
�S�Ddiv�i���U�j��Gauss�̔��U�藝�C���i���v���V�A���j
3.(6)�ŁA�u�i�r�j�͔C�ӂł����B�u���i�r���j�C�ӂɏ�����������Ɍ����l����A3.(5)���Č��ł���͂��ł��B3.(6)�̍ʼnE�ӂ́A���炩��3.(5)�̉E�ӂɂȂ�܂��B�ł͍ō��ӂ́H�B���̂��߂ɐ}-1���l���܂��B
�@�}-1�ł́A�_(x�Cy) �ɂ����闬����(vx�Cvy) �Ƃ��A�e�ӂ̒���dvx�Cdy �́A�ŏ���������Ƃ��Ă����܂��B�}-1�ŁA3.(6)�̍ō��ӂ̌v�Z���s���܂��B�}-1�̒����`�u�́A3.(6)�̍ʼnE�ӂɏo�Ă���ϕ��̈�u�ɑ������܂��B�]���āA3.(6)�̍ō��ӂɏo�Ă���ϕ��̈�r�Ƃ́A�}�̕Ӈ@�`�C�ł��B
�@3.(6)�� u�ds ��u�Ƃ́A�r��̗����ł��B(x�Cy) �ɂ����闬����(vx�Cvy) �ł����Adx��dy�������Ȏ�����A�u�S�̂ŗ����͈�肾�Ƃ݂Ȃ��Ă��\��Ȃ����炢�ł��i�ǂ����Ɍ����Ƃ�j�B��������Ƈ@��ł̗���u���Au��(vx�Cvy) �Ƃ����܂��B
�@3.(6)�� u�ds ��ds �Ƃ́A�r�̐��f�x�N�g���ł��B���f�x�N�g���̒�`�́Ads��|dL|n�ŁA|dL|�͍l���Ă���Ȑ��̔����v�f�i���f�j�ł����B���ܕӇ@�͔����Ȃ̂ŁA|dL|��dy �Ƃ����܂��B���n�́A�l���Ă���Ȑ��̊O�@�������̒P�ʃx�N�g���ł����B�Ӈ@�̂���́A(�|1�C0) �ł��B����ć@��ł́A
�@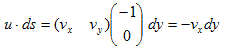
�ƂȂ�܂����A���ۂɂ́A�����Ă��Ȃ�z������dz ������̂ŁA
�@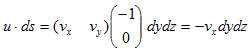
���A3�����ł̌��ʂɂȂ�܂��B
�@
�ӇA�ɂ��āA������������A
�@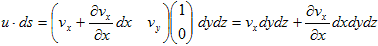
�ƂȂ�܂��B������vx ���A
�@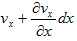
�ɕς�����̂́A1.�ŏq�ׂ������̍l�����g���Ă��܂��B�@�{�A����A
�@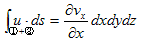
�������܂��B�B�{�C������A
�@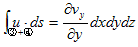
�������A���ۂɂ�z�����ɁA�D�C�E������̂Łi�����ĂȂ����ǁj�A
�@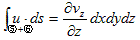
�������܂��B3.(6)�̍ō��ӂ̐ϕ��Ƃ́A�����̍��v�ł��B���̂Ȃ�A2�����̒����`�́A3�����ł͒����̂ɂȂ�A�����̂�6�ʑ̂Ȃ̂ŁA�@�{�A�{�B�{�C�{�D�{�E�ł��B
�@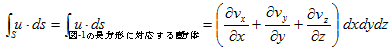
�@����A3.(6)�̍ʼnE�ӂ̐ϕ��́A�u��C�ӂɏ����������ꍇ�A��dv�ɂȂ�܂����A
�}-1�ɂ�����dv �Ƃ́Adv��dxdydz �̎��Ȃ̂ŁA
�@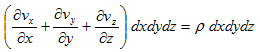
���Ȃ킿�A
�@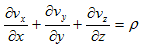 �@�@�@(1)
�@�@�@(1)
�����_�ł��i�����ŋɌ�����������ɂȂ�܂��j�B
�@(1)�̍��ӂ��J�b�R�ǂ����܂��傤�B
�@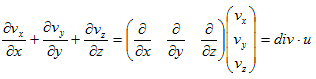
�@����́A�x�N�g����p�fdiv ���A
�@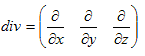
�Œ�`�����A�Ƃ������ł��B�����(1)���A
�@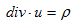 �@�@�@(2)
�@�@�@(2)
�Ə����܂��B(2)��3.(6)�̕����I�Ӗ��́A���炩�ɓ����Ȃ̂ŁA��������ʕۑ����ƌĂ�܂��B
�@(2)�͖{���I�ɁA3.(6)�A
�@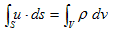
�Ɠ����ł��B���������(2)�ɂ����ẮA�ς���_�̗N���o�����x�ł���悤�ɁAdiv�u �́A��_�̗��o���x���x�ł��鎖�ɂȂ�܂��B��_�ɐ����A���x�ςŋ��������Ȃ�A����͂��̈�_����Adiv�u �̐����ŎU�킵�Ă����i�����o���Ă����j�Ƃ����̂�(2)�ł��B�U��i�����o���j�U�ƌ����Ă������ł��傤�Bdiv��divergence�̗��ŁA���{���ł͔��U�ł��B(2)��3.(6)�ƌ��ѕt���܂��B(2)��̐ςu�Őϕ�����ƁA
�@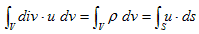
���Ȃ킿�A
�@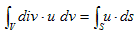 �@�@�@(3)
�@�@�@(3)
�������܂��B(3)�� Gauss�̔��U�藝�ƌ����܂��B�Ƃ���ŁA�ǂ��ł��傤���H�B�����v�f��0�Ƃ����Ȃ��Ŏc�����R�́A�킩���Ē������ł��傤���H�B
�@div �ƃ��v���V�A�����Ƃ̊W�́A���̂悤�ɂȂ�܂��B�Q�D�ŏq�ׂ��悤�ɁA���x�|�e���V�����ӂƂ́A
�@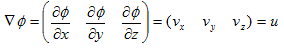 �@�@�@(4)
�@�@�@(4)
�ƂȂ�X�J���[���ł��B(4)��(2)�ɑ�����܂��B
�@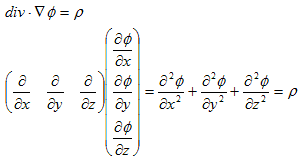 �@�@�@(5)
�@�@�@(5)
�������܂��B���ӂ́A
�@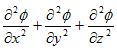
���A
�@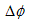
�Ə����A�������v���V�A���ƌĂԎ��ɂ���ƁA(5)����A�k���Q�Ȃ����S���̂̎x�z�������A
�@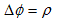 �@�@�@(6)
�@�@�@(6)
�ƁA�x�N�g����͂̌����A
�@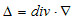 �@�@�@(7)
�@�@�@(7)
�������܂��B
�@(7)����͎��R�ɁA�x�N�g����p�f�Ԃ̓��ρA
�@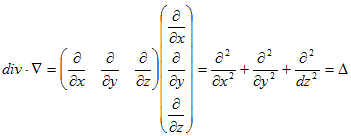 �@�@�@(8)
�@�@�@(8)
��������A���̌��ʂƂ��āA�����X�J���[��p�f�Ƃ݂Ȃ��鎖�A
�@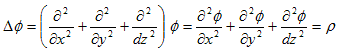
���o�Ă��āA�X�J���[������X�J���[�̃��ӂ́A�X�J���[�ςɂȂ�ƁA�ǂ߂�悤�ɂȂ�܂��B
�@�����H�Adiv���� �ł͂Ȃ������āH�B�E�E�E���̒ʂ�ł��i(8)���ēx���Ă݂ĉ������j�B����āA
�@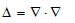 �@�@�@(9)
�@�@�@(9)
���x�N�g����͂̌����ł��B�������A(9)�̍Ō�́ނ̓X�J���[�ɍ�p���鎖��z�肵�A�ŏ��́ނ̓x�N�g���ɍ�p����̂�O��Ƃ��Ă��܂��B���ς�ʂ��ăx�N�g���ɍ�p����ނ́Adiv�Ə����̂����킵�ł��B����́A���ʕۑ���(2)�̓��o�ߒ��ɂ����Č���܂����B
�@(2)�͗��ʕۑ����Ƃ����A���̗͊w�̍������Ȃ��@����\�킵�A���������܂ł���ė����悤�ɁA���̓��o�͔��ɖ��m�ȕ����I�C���[�W�Ɏx����ꂽ���̂ŁA���̉ߒ��� div �͊J�����ꂽ�̂ł����B�����Ƀx�N�g����͂�p�����O�̗��R������܂��B
�@�@�B �������������ŁA�����I�C���[�W�������D
�����̗��R�ł��B����������A�ł͂���܂����B
�@�ȏ���܂Ƃ߂܂��B
�@�|�e���V�����͂ӂ��A���炩�̕ۑ����ƊW����ƁA�Q�D�ŏq�ׂ܂����B�����č�����͗��ʕۑ����ŁAGauss�̔��U�藝�Ƃ������w�I�藝�����̂ł����B���������̉ߒ��ŁAdiv �Ƃ����V���ȃx�N�g����p�f���J������܂����B����āA
�E�|�e���V�����ӂ̌��z�A�ރ�
� �ۑ���
�@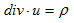
�܂��́A
�@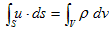
�E Gauss�̔��U�藝
�@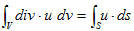
�E �x�N�g����͂̌���
�@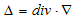
�͈�ʓI�ɁA�g�ɂȂ��ĕp�ɂɌ���܂��B
NO.1743�@�@�@�Ɍ��l�́H�@�@2008.10.8.�@�@���̗���
��Q�P�S�w�I�ȉ�����

���F���̋L���Ɋւ��铊�e�̌f�ڂ́A�Q�O�O�W�N10��27���ȍ~�Ƃ��܂��B
NO.1742�@�@�ŏ����{��(2) �@�@2008.10.8.�@�@��ӂ����̂炢��������
�悸�A�Ղ����ꍇ���l���܂��B
�i�P�j
�@����f���Ƃ��܂��B
�@A��p �̌`�̂Ƃ��A���߂鐮���̑g�́A(1,p) �݂̂ł��B
�@N(p)��1
�i�Q�j
�@A��pk �̌`�̂Ƃ��A
�@���߂鐮���̑g�́A���̒ʂ�ł��B
�@(1,pk), (p,pk), (p2,pk), ������, (pk-1,pk)
�@N(pk)��k
�i�R�j
�@��ʂ̏ꍇ�����ʂ���悤�ɁAA���f���V�̏ꍇ�����Ă݂܂��B
�@a,b,c,��������f���Ƃ��܂��B
�@A��abcdefg�@�Ƃ��܂��B
�P��A�̖́A27����܂��B
���߂鐮���̑g�ŁA(A�̖�, A) �̌`�̂��̂́A
(1,A),(a,A),(b,A),���,(ab,A),(ac,A),���,(bcdefg,A)�@�@�@�m(abcdefg,A) �ȊO�n
�̂悤�ɁA�Q7�|1 ����܂��B
�Q��
���P������[�P]�̑f���A��Q������[�U]�̑f���̐ς̏ꍇ�́A
�@(a,bcdefg), (b,acdefg), (c,abdefg), ���, (g,abcdef) �̂悤��7C1����܂��B
���P������[�Q]�̑f���A��Q������[�T]�̑f���̐ς̏ꍇ�́A
�@(ab,cdefg), (ac,bdefg), ���, (bc,adefg), (bd,acefg), ���, (fg,abcde) �̂悤��7C2����܂��B
���P������[�R]�̑f���A��Q������[�S]�̑f���̐ς̏ꍇ�́A
�@(abc,defg), (abd,cefg), ���, (acd,befg), (ace,bdfg), ���, (efg,abcd) �̂悤��
7C3����܂��B
���@�ς̒l����P�����̕����傫���Ȃ�A��Q�����Ɠ���ւ���ƍl���Ă����܂��B
����7C0�{7C1�{7C2�{7C3�{7C4�{7C5�{7C6�{7C7���Q7 �ł��B
�W���̒l�͍��E�Ώ̂œ������A���[�̒l�͂P�ł��B
������A[�Q]�̂R�̒l�̍��v�́A
7C1�{7C2�{7C3���Q7�^�Q�|�P���Q6�|�P �ł��B
�R��
�Q�̐����ɋ��ʈ���������ꍇ���l���܂��B
a)
�E���ʑf�������P�ŁA���̕����̑f�����̌����A��P����[�P]�Ƒ�Q����[�T]�̏ꍇ�́A
�@(a�b, a�cdefg),�@(a�c, a�bdefg),�@���,�@(a�g, a�bcdef)
�@(b�a, b�cdefg),�@(b�c, b�adefg),�@���,�@(b�g, b�acdef)
�@������
�@(g�a, g�bcdef),�@(g�b, g�acdef),�@���,�@(g�f, g�abcde)
���Ă͋��ʂ̈����̑I�ѕ��Ȃ̂�7C1�A���͎c��̑�P�����̈����̑I�ѕ��Ȃ̂�6C1����܂��B
������A7C1�~6C1����܂��B
�E���ʑf�������P�ŁA�f�̕����̑f�����̌����A��P����[�Q]�Ƒ�Q����[�S]�̏ꍇ�́A
�@(a�bc, a�defg),�@(a�bd, a�cefg),�@���,�@(a�fg, a�bcde)
�@(b�ac, b�defg),�@(b�ad, b�cefg),�@���,�@(b�fg, b�acde)
�@������
�@(g�ab, g�cdef),�@(g�ac, g�bdef),�@���,�@(g�ef, g�abcd)
���Ă͋��ʂ̈����̑I�ѕ��Ȃ̂�7C1�A���͎c��̑�P�����̈����̑I�ѕ��Ȃ̂�6C2����܂��B
������A7C1�~6C2����܂��B
�E���ʑf�������P�ŁA�f�̕����̑f�����̌����A��P����[�R]�Ƒ�Q����[�R]�̏ꍇ�́A
�@(a�bcd, a�efg),�@(a�bce, a�dfg),�@���,�@(a�bfg, a�cde)
�@(b�acd, b�efg),�@(b�ace, b�dfg),�@���,�@(b�afg, b�cde)
�@������
�@(g�abc, g�def),�@(g�abd, g�cef),�@���,�@(g�aef, g�bcd)
���Ă͋��ʂ̈����̑I�ѕ��Ȃ̂�7C1�A���͎c��̑�P�����̈����̑I�ѕ��Ȃ̂�6C3�^�Q����܂��B
���@���͒��ӂ��K�v�ł��B�������ɕ�����Ƃ��́A������ւ��������̂������Ȃ̂łQ�Ŋ���܂��B
������A7C1�~6C3�^�Q����܂��B
����6C0�{6C1�{6C2�{6C3�{6C4�{6C5�{6C6���Q6 �ł��B
�W���̒l�͍��E�Ώ̂œ������A���[�̒l�͂P�ł��B
������6C1�{6C2�{6C3�^�Q���Q6�^�Q�|�P�ł��B
����āA[�R]a)�̂R�̒l�̍��v�́A
7C1�~6C1�{7C1�~6C2�{7C1�~6C3�^�Q7��7C1�~(6C1�{6C2�{6C3�^�Q)��7C1�~(�Q5�|�P)
���j
�E���ʑf�������Q�ŁA�f�̕����̑f�����̌����A��P����[�P]�Ƒ�Q����[�S]�̏ꍇ�́A
�@(ab�c, ab�defg),�@(ab�d, ab�defg),�@���,�@(ab�g, ab�cdef)
�@(ac�b, ac�defg),�@(ac�d, ac�defg),�@���,�@(ac�g, ac�bdef)
�@������
�@(fg�a, fg�bcde),�@(fg�b, fg�acde),�@���,�@(fg�e, fg�abcd)
���Ă͋��ʂ̈����̑I�ѕ��Ȃ̂�7C2�A
���͎c��̑�P�����̈����̑I�ѕ��Ȃ̂�5C1����܂��B
������A7C2�~5C1����܂��B
�E���ʑf�������Q�ŁA�f�̕����̑f�����̌����A��P����[�Q]�Ƒ�Q����[�R]�̏ꍇ�́A
�@(ab�cd, ab�efg),�@(ab�ce, ab�cfg),�@���,�@(ab�fg, ab�cde)
�@(ac�bd, ac�efg),�@(ac�be, ac�bfg),�@���,�@(ac�fg, ac�bde)
�@������
�@(f�@g�ab, fg�cde),�@(fg�ac, fg�bde),�@���,�@(fg�de, fg�abc)
���Ă͋��ʂ̈����̑I�ѕ��Ȃ̂�7C2�A
���͎c��̑�P�����̈����̑I�ѕ��Ȃ̂�5C2����܂��B
������A7C2�~5C2����܂��B
����āA[�R]b)�̂Q�̒l�̍��v�́A
7C2�~5C1�{7C2�~5C2��7C2�~(5C4�{5C2)��7C2�~(�Q4�|�P)
c)
�E���ʑf�������R�ŁA�f�̕����̑f�����̌����A��P����[�P]�Ƒ�Q����[�R]�̏ꍇ�́A
�@(abc�d, abc�efg),�@(abc�e, abc�dfg),�@���,�@(abc�g, abc�def)
�@(abd�c, abd�efg),�@(abd�e, abd�cfg),�@���,�@(abd�g, abd�cef)
�@������
�@(efg�a, efg�bcd),�@(efg�b, efg�acd),�@���,�@(efg�d, efg�abc)
���Ă͋��ʂ̈����̑I�ѕ��Ȃ̂�7C3�A
���͎c��̑�P�����̈����̑I�ѕ��Ȃ̂�4C1����܂��B
������A7C3�~4C1����܂��B
�E���ʑf�������R�ŁA�f�̕����̑f�����̌����A��P����[�Q]�Ƒ�Q����[�Q]�̏ꍇ�́A
�@(abc�de, abc�fg),�@(abc�df, abc�eg),�@���,�@(abc�fg, abc�de)
�@(abd�ce, abd�fg),�@(abd�cf, abd�eg),�@���,�@(abd�fg, abd�ce)
�@������
�@(efg�ab, efg�cd),�@(efg�ac, efg�bd),�@���,�@(efg�cd, efg�ab)
���Ă͋��ʂ̈����̑I�ѕ��Ȃ̂�7C3�A
���͎c��̑�P�����̈����̑I�ѕ��Ȃ̂�4C2�^�Q����܂��B
������A7C3�~4C2�^�Q����܂��B
����āA[�R]��)�̂Q�̒l�̍��v�́A
7C3�~4C1�{7C3�~4C2�^�Q��7C3�~(4C1�{4C2�^�Q)��7C3�~(�Q3�|�P)���V�~7C3
���j
�E���ʑf�������S�ŁA�f�̕����̑f�����̌����A��P����[�P]�Ƒ�Q����[�Q]�̏ꍇ�́A
�@(abcd�e, abcd�fg),�@(abcd�f, abcd�eg),�@(abcd�g, abcd�ef)
�@(abce�d, abce�fg),�@(abce�f, abce�dg),�@(abce�g, abce�df)
�@������
�@(defg�a, defg�bc),�@(defg�b, defg�ac),�@(defg�c, defg�ab)
���Ă͋��ʂ̈����̑I�ѕ��Ȃ̂�7C4�A
���͎c��̑�P�����̈����̑I�ѕ��Ȃ̂�3C1����܂��B
������A7C4�~3C1����܂��B
7C4�~3C1��7C4�~(�Q2�|�P)���R�~7C4
���j
�E���ʑf�������T�ŁA�f�̕����̑f�����̌����A��P����[�P]�Ƒ�Q����[�P]�̏ꍇ�́A
�@(abcde�f, abcde�g)
���Ă͋��ʂ̈����̑I�ѕ��Ȃ̂�7C5�A
���͎c��̑�P�����̈����̑I�ѕ��Ȃ̂�2C1�^�Q����܂��B
������A7C5�~�^�Q����܂��B
7C5�~2C1�^�Q��7C5�~(�Q1�|�P)���P�~7C5
����āA�i�R�j[�P]����[�R]���j�܂ł�������ƁA
�i�Q7�|�P�j�{7C0�i�Q6�|�P�j�{7C1�i�Q5�|�P�j�{7C2�i�Q4�|�P�j�{7C3�i�Q3�|�P�j�{7C4�i�Q2�|�P�j�{7C5�i�Q1�|�P�j
���Q7�{�i7C0�Q6�{7C1�Q5�{7C2�Q4�{7C3�Q3�{7C4�Q2�{7C5�Q1�j�|�i7C0�{7C1�{7C2�{7C3�{7C4�{7C5�j
���Q7�{�i7C0�Q6�{7C1�Q5�{7C2�Q4�{7C3�Q3�{7C4�Q2�{7C5�Q1�j�|�i7C0�{7C1�{7C2�{7C3�{7C4�{7C5�{7C6�{7C7�j�{7C6�{7C7
���Q7�{�i7C0�Q7�{7C1�Q6�{7C2�Q5�{7C3�Q4�{7C4�Q3�{7C5�Q2�{7C6�Q1�{7C7�Q0�j�^�Q�|�Q7�|�P�^�Q
���i7C0�Q7�{7C1�Q6�{7C2�Q5�{7C3�Q4�{7C4�Q3�{7C5�Q2�{7C6�Q1�{7C7�Q0�j�^�Q�|�P�^�Q
���i�Q�{�P�j7�^�Q�|�P�^�Q
���i�R7�|�P�j�^�Q
�ł��B
�܂�A[��] �̑f��������Ȃ�`�ɂ��āA���̐����̑g���m�i[��]�j�ŕ\���ƁA
�m�i[��]�j���i�Rn�|�P�j�^�Q
�܂��A
�@�i�Rn�{1�|�P�j�^�Q
���R�~�i�Rn�|�R�^�R�j�^�Q
���R�~�i�Rn�|�P�^�R�j�^�Q
���R�~�i�Rn�|�P�{�Q�^�R�j�^�Q
���R�~�i�Rn�|�P�j�^�Q�{�R�~�i�Q�^�R�j�^�Q
���R�~�i�Rn�|�P�j�^�Q�{�P
���
�@�m�i[���{�P]�j���R�m�i[��]�j�{�P
�ł��B
�ȏォ��
���P�@�m�i�U�j���m�i2�~3�j���m�i[�Q]�j���i�R2�|�P�j�^�Q���S
���Q�@�m�i�P�T�j���m�i3�~5�j���m�i[�Q]�j���i�R2�|�P�j�^�Q���S
���R�@�m�i�R�T�j���m�i5�~7�j���m�i[�Q]�j���i�R2�|�P�j�^�Q���S
���S�@�m�i�P�O�T�j���m�i3�~5�~7�j���m�i[�R]�j���R�m�i[�Q]�j�{�P���P�R
���T�@�m�i�Q�P�O�j���m�i2�~3�~5�~7�j���m�i[�S]�j���R�m�i[�R]�j�{�P���S�O
���U�@�m�i�Q�R�P�O�j���m�i2�~3�~5�~7�~11�j���m�i[�T]�j���R�m�i[�S]�j�{�P���P�Q�P
�ƂȂ�܂��B
���ɁA��ʂ̏ꍇ���l���܂��B
��ʂ̏ꍇ�����ʂ���悤�ɁAA���f���T��ނ̏ꍇ�����Ă݂܂��B
a,b,c,��������f���Ƃ��܂��B
�,�,�,�������𐳂̐����Ƃ��܂��B
A��a�b�c�d�e��@�Ƃ��܂��B
�P�� A�̖́A(��{1)(��{1)(��{1)(��{1)(��{1) ����܂��B
���߂鐮���̑g�ŁA(A�̖�, A) �̌`�̂��̂́A
(��{1)(��{1)(��{1)(��{1)(��{1)�|�P ����܂��B
�Q�� ���ɐ����̑g�̑�Q������A�ł͂Ȃ��A��P�����Ƒ�Q�����̊e�f���̎������قȂ���̂𐔂��܂��B
�����ŁA�� ��0�`�-1�Aj ��0�`�-1�Ak ��0�`�-1�Al ��0�`�-1�Am ��0�`�-1�̂��鐮���Ƃ��܂��B
�E�ia��bjckdlem, b�c�d�e��ai�j�̌`�̂��̂́A
�@�ia��bjckdlem, b�c�d�e��ai�j
�@�ib��aickdlem, a�c�d�e��bj�j
�@�ic��aibjdem, a�b�d�e��ck�j
�������
�@���v 5C1�~�������
�E�ia�b��ckdlem, c�d�e��aibj�j�̌`�̂��̂́A
�@�ia�b��ckdlem, c�d�e��aibj�j
�@�ia�c��bjdlem, b�d�e��aick�j
�@�ia�d��bjckem, b�c�e��aidl�j
�������
�@���v5�b2�~����� ����܂��B
�Q���̍��v�́A
�@5�b1�~������{5�b2�~�����
���i5�b1�{5�b2�j�~�����
���i�Q5�^�Q�|�P�j�~�����
���i�Q4�|�P�j�~�����
�R�� ���ɐ����̑g�̑�Q������A�ł͂Ȃ��A��P�����Ƒ�Q������a�,b�,����̌`�̋��ʂ̈�����������̂𐔂��܂��B
�����ŁA�� ��0�`�-1�Aj ��0�`�-1�Ak ��0�`�-1�Al ��0�`�-1�Am ��0�`�-1�̂��鐮���Ƃ��܂��B
���j ���ʈ������P��ނ̂���
�E�ia��b��ckdlem, a��c�d�e��bj�j�̌`�̂��̂́A
�@�ia��b��ckdlem, a��c�d�e��bj�j
�@�ia��c��bjdlem, a��b�d�e��ck�j
�������
�@�ib��a��ckdlem, b��c�d�e��ai�j
�@�ib��c��aidlem, b��a�d�e��ck�j
�������
�������
�@�Q�߂̈����̑I�ѕ���4�b1�Ȃ̂ŁA
�@4�b1�~(�����{�����{�����{�����{����)
�E�ia��b�c��dlem, a��d�e��bjck�j�̌`�̂��̂́A
�@�ia��b�c��dlem, a��d�e��bjck�j
�@�ia��b�d��ckem, a��c�e��bjdl�j
�������
�������
�@�Q�߂̈����̑I�ѕ���4�b2�^�Q�Ȃ̂ŁA
�@4�b2�^�Q�~(�����{�����{�����{�����{����)
�R�����j�̍��v�́A
�@�i4�b1�{4�b2�^�Q�j�~(�����{�����{�����{�����{����)
���i�Q4�^�Q�|�P�j�~(�����{�����{�����{�����{����)
���i�Q3�|�P�j�~(�����{�����{�����{�����{����)
���j ���ʈ������Q��ނ̂���
�E�ia�b��c��dlem, a�b��d�e��ck�j�̌`�̂��̂́A
�@�ia�b��c��dlem, a�b��d�e��ck�j
�@�ia�b��d��ckem, a�b��c�e��dl�j
�������
�@�ia�c��b��dlem, a�c��d�e��bj�j
�@�ia�c��d��bjem, a�c��b�e��dl�j
�������
�������
�@�Q�߂̈����̑I�ѕ���3�b1�Ȃ̂ŁA
�@3�b1�~(����{����{����{����{����{����{����{����{����{���)
���i�Q3�^�Q�|�P�j�~(����{����{����{����{����{����{����{����{����{���)
���i�Q2�|�P�j�~(����{����{����{����{����{����{����{����{����{���)
���j ���ʈ������R��ނ̂���
�E�ia�b�c��d��em, a�b�c��e��dl�j�̌`�̂��̂́A
�@�ia�b�c��d��em, a�b�c��e��dl�j
�@�ia�b�d��c��em, a�b�d��e��ck�j
�������
�������
�@�Q�߂̈����̑I�ѕ���2�b1�^�Q�Ȃ̂ŁA
�@2�b1�^�Q�~(���{���{���{���{���{���{���{���{���{��)
���i�Q1�|�P�j�~(���{���{���{���{���{���{���{���{���{��)
����ĂP���A�Q���A�R�������킹��ƁA
| N�iA) | ���o(�+1)(�+1)(�+1)(�+1)(�+1)-1�p
|
| �@�{�i�Q4�|�P�j�~�����
|
| �@�{(�Q3�|�P)�~(�����{�����{�����{�����{����)
|
| �@�{(�Q2�|�P)�~(����{����{����{����{����{����{����{����{����{���)
|
| �@�{(�Q1�|�P)�~(���{���{���{���{���{���{���{���{���{��)
|
| ���Q4�~�����
|
| �@�{�Q3�~(�����{�����{�����{�����{����)
|
| �@�{�Q2�~(����{����{����{����{����{����{����{����{����{���)
|
| �@�{�Q1�~(���{���{���{���{���{���{���{���{���{��)
|
| �@�{�Q0�~�i��{��{��{��{��j
|
����āA��ʂɂ́Ap1,p2,p3,�E�E�E��f���Am1,m2,m3,����𐳂̐����Ƃ��āA
A��p1m1p2m2p3m3������pnmn �̂Ƃ�
| N�iA) | ���i�i�e�w���{�P�j�̂����̊�{�Ώ̎��|�P�j
|
| �@�{�i�Qn-1�|�P�j�~�i�e�w���̂����̊�{�Ώ̎��j
|
| �@�{�i�Qn-2�|�P�j�~�i�e�w����n-1���̊�{�Ώ̎��j
|
| �@�{�i�Qn-3�|�P�j�~�i�e�w����n-�Q���̊�{�Ώ̎��j
|
| �@�{������
|
| �@�{�i�Q1�|�P�j�~�i�e�w���̂Q���̊�{�Ώ̎��j
|
| ���Qn-1�~�i�e�w���̂����̊�{�Ώ̎��j
|
| �@�{�Qn-2�~�i�e�w����n-1���̊�{�Ώ̎��j
|
| �@�{�Qn-3�~�i�e�w����n-�Q���̊�{�Ώ̎��j
|
| �@�{������
|
| �@�{�Q1�~�i�e�w���̂Q���̊�{�Ώ̎��j
|
| �@�{�Q0�~�i�e�w���̂P���̊�{�Ώ̎��j
|
NO.1741�@�@�@�ȉ~�ϕ��Ɋւ���h �R��̊��Ⴂ�h �W���` �@�@2008.10.1.�@�@�{���ӗ�
�n�}���e�̃v���O�������쐬���ɑȉ~�ϕ��̌v�Z�ɐڂ���@�����C�����̋��ȏ���T�C�g�Ɂi������
�ށj���S�҂��܂����₷���i�s�e�E�s���Ăȁj�L�ڂ�����Ɗ����܂����̂œ��e���܂����B���͂��̕�
��Ɋւ��Ă��f�l���R�ł��̂ŁC���̕��̃t�H���[������K���ł��B
�ȉ~�ϕ��́h ��P�튨�Ⴂ�h �W���`�@���@�y�˂��C�ǂ��ɂR�`�S�����������Ă�́H�z
�@�ȉ~�ϕ��̒�`�𐳂����ǂ܂Ȃ��Ɓu���`�ށC�W���`���č����̂Ȃ��̂ǂ����R�`�S�����Ȃ́H�v�ƍ��f
���Ă��܂��܂��B�ȉ~�ϕ��̒�`�ɍ������ϕ��� Legendre-Jacobi �̂R�̕W���`�ɒ�����i����炪
�O�p�����܂`�ŕ\���ł���j�Ƃ��������ł��B���������ȉ~�ϕ��̒�`�ɍ����Ă��Ă������I�ɋ���
����ϕ�������܂����i�[�ȉ~�ϕ��C���̏ꍇ��L�W���`�ɒ������Ƃ������I�ɉ�����j�C�܂��C�ȉ~��
���̕W���`��Legendre-Jacobi ���̂P�Z�b�g�����ł͂���܂���B
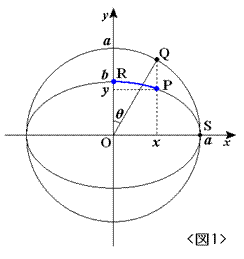
�ȉ~�ϕ��́h ��Q�튨�Ⴂ�h �W���`�@���@�y�ȉ~�̌ʒ������܂��ł���ˁH�z
�@�ȉ~�S���̂P���i�܂��͑S�́j�̌ʒ����C��Q�튮�S�ȉ~�ϕ��̒l���̂��́i�܂��͂��̒萔�{�j�Ƃ���
���܂������Ȃ���Ă��邱�Ƃ������ł����C������Z�������̌ʒ������߂鎮�����܂茩�����܂���B
���p��E�����ǂ���̊ϓ_������C��҂̒���]���������̂ł��B
x2/a2 + y2/b2 = 1(a>b)�ŁC�_(a,0)
����X�^�[�g���C����̊e�_�ɂ�����ȗ����a��`��������x ���ƂȂ��p���ӂƂȂ�_�܂ł̎���s( �� ) �́F
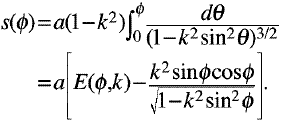
�����ŁCk ���ȉ~�̗��S���CE( �� ,k) ����Q��ȉ~�ϕ��ɂ�����B�m���ɁC�� = �� /2 �܂ōs���Ɓm �n��
�̑�Q����0 �ƂȂ�C��������́i���S�j�ȉ~�ϕ������ɂȂ�܂��B
�ȉ~�ϕ��́h ��R�튨�Ⴂ�h �W���`�@���@�y��R�풴����I���Ԃ͂��ꂶ���H�z
�@��P��Ƒ�Q��͋����W�J����ƌ݂��ɂƂĂ������`�������Ă��܂����C��R��͌ÓT�I�ȋ��ȏ��ł�
�ȉ~����p������ϖʓ|�Ȍv�Z������Ă��܂��B�Ƃ��낪�CCarlson �Ƃ��������҂�1970 �N��
�ɊJ��������@�ɂ��C��P��`��R������ʂ��ǂ��Ȍ��Ɍv�Z�ł���悤�ɂȂ�܂����B���݂̎��p�I
�Ȑ��l�v�Z�v���O�����ł́C���̂�肩���̕����]���̂��̂����嗬�ɂȂ��Ă��܂��B����������́C
"Numerical Recipes" �̃T�C�g�����������������B
�Q�lC �v���O����
�@�ÓT�I�i�����W�J�j�ȕ��@�ɂ���Q��ȉ~�ϕ�elle( �� ,k2)�B��Q�����ɂ�k �łȂ�k2 �����Ďg���B
�v�Z�@������̒l�ɂ����Ǝv�����C�L������10 �`14 �����x�͐������o��Belle() ����a[] �̊e�l����
��return �̍s�̕����P�����������邾���ő�P��ȉ~�ϕ�ellf( �� ,k2) �ƂȂ�Bepoly(x,c[],d) �́C���W
��c[] �����P�ϐ�d ���������̒l��x �ɂ����ĕ]������Bc[0] �ɒ萔���Cc[d] �ɍō����̌W�����i�[�i��
�܂�C�Ăяo�����̔z��̑傫����d+1 �ȏ�K�v�j�B�Ȃ��C�����̃G���[�`�F�b�N�͈�Ȃ��̂Œ��ӊ肢
�܂��B
double elle(double phi,double ks) {
double a[16],b[16],c[16] ;
double sp,cp,pw = 1. ;
int m = 7,i ;
c[ 0] = 1. ;
c[ 1] = 6.66666666666666666666666666666666666666666666667e-1 ;
c[ 2] = 5.33333333333333333333333333333333333333333333333e-1 ;
c[ 3] = 4.571428571428571428571428571428571428571428571429e-1 ;
c[ 4] = 4.063492063492063492063492063492063492063492063492e-1 ;
c[ 5] = 3.694083694083694083694083694083694083694083694084e-1 ;
c[ 6] = 3.409923409923409923409923409923409923409923409923e-1 ;
c[ 7] = 3.182595182595182595182595182595182595182595182595e-1 ;
c[ 8] = 2.995383701266054207230677818913113030760089583619e-1 ;
c[ 9] = 2.837731927515209248955378986338738660720084868692e-1 ;
c[10] = 2.702601835728770713290837129846417772114366541611e-1 ;
c[11] = 2.585097408088389377930365950287877868978959300672e-1 ;
c[12] = 2.4816935117648538028131513122763627542198009286446e-1 ;
c[13] = 2.3897789372550444027089605229327937633227712646208e-1 ;
c[14] = 2.307372767004870457787961884210973288725434324461e-1 ;
c[15] = 2.232941387424068184956092146010619311669775152705e-1 ;
a[ 0] = 0. ;
a[ 1] = 2.5e-1 ;
a[ 2] = 4.6875e-2 ;
a[ 3] = 1.953125e-2 ;
a[ 4] = 1.068115234375e-2 ;
a[ 5] = 6.7291259765625e-3 ;
a[ 6] = 4.62627410888671875e-3 ;
a[ 7] = 3.3752918243408203125e-3 ;
a[ 8] = 2.571023069322109222412109375e-3 ;
a[ 9] = 2.02349037863314151763916015625e-3 ;
a[10] = 1.633968480746261775493621826171875e-3 ;
a[11] = 1.34701120623503811657428741455078125e-3 ;
a[12] = 1.12952502189500592066906392574310302734375e-3 ;
a[13] = 9.607646266118763378472067415714263916015625e-4 ;
a[14] = 8.2718893235078638781487825326621532440185546875e-4 ;
a[15] = 7.19654371145184157398944080341607332229614257812e-4 ;
b[0] = epoly(ks,a,m-1) ;
for(i=1; i<m; i++)
b[i] = b[i-1] - a[i]*(pw*=ks) ;
for(i=1; i<m; i++)
b[i] *= c[i] ;
sp = sin(phi) ;
cp = cos(phi) ;
return(phi*(1. - b[0]) + sp*cp*epoly(sp*sp,b,m-1)) ;
}
double epoly(double x,double *c,int d) {
double e = 0. ;
while(d > 0)
e = (e + c[d--])*x ;
return(e+c[0]) ;
}

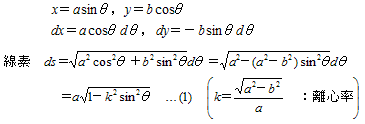
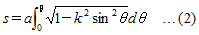
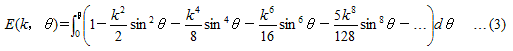

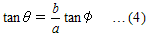
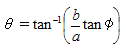 �@�ŃƂ����߂�B�@
�@�ŃƂ����߂�B�@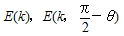 �@�����߂�B
�@�����߂�B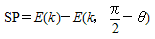
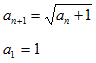
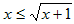
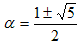
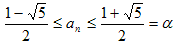
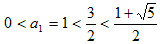
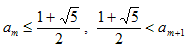
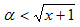
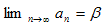
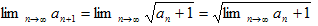 �@�@�i��̑o�A�������g���Ă��܂��j
�@�@�i��̑o�A�������g���Ă��܂��j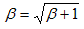
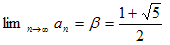

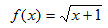
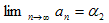 �@�@�@(6)
�@�@�@(6)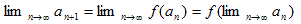
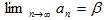
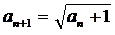
 �� �K���ɂ���
�� �K���ɂ���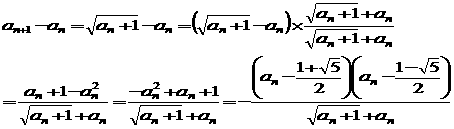
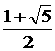 �@�@���召�̋��ڂɂȂ�܂��B
�i�_�`��X���W�A���̒l�����Ƃ���j�܂�A
�@�@���召�̋��ڂɂȂ�܂��B
�i�_�`��X���W�A���̒l�����Ƃ���j�܂�A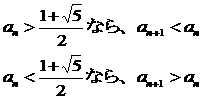
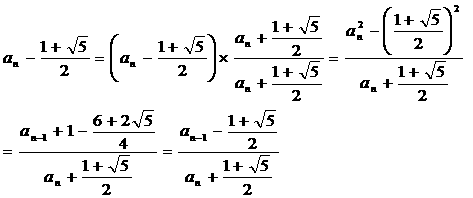
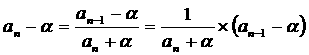
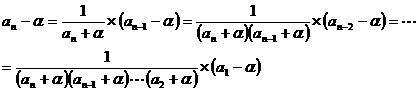
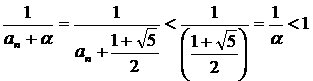
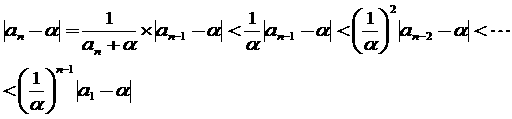
 �@�@�Ȃ̂ŁA
�@�@�Ȃ̂ŁA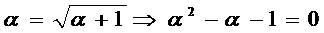 �@�@�@�i�������A���̉��j
�@�@�@�i�������A���̉��j
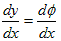
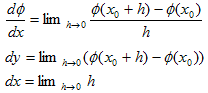
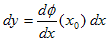 �@�@�@(1)
�@�@�@(1)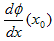
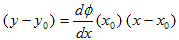 �@�@�@(2)
�@�@�@(2)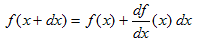 �@�@�@(3)
�@�@�@(3)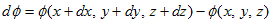 �@�@�@(4)
�@�@�@(4)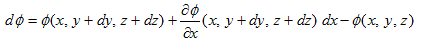
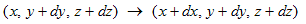
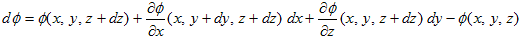
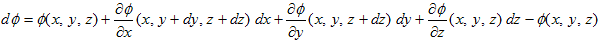
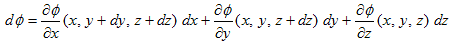 �@�@�@(5)
�@�@�@(5)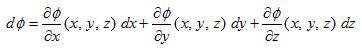
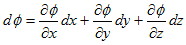 �@�@�@(6)
�@�@�@(6)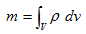 �@�@�@(7)
�@�@�@(7)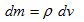 �@�@�@(8-1)
�@�@�@(8-1)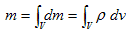 �@�@�@(8-2)
�@�@�@(8-2)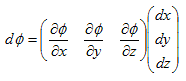 �@�@�@(9)
�@�@�@(9)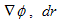
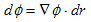 �@�@�@(10)
�@�@�@(10)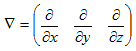
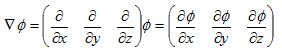
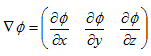
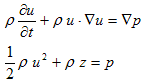 �@�@�@(1)
�@�@�@(1)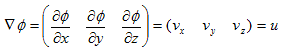 �@�@�@(2)
�@�@�@(2)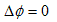

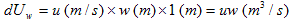
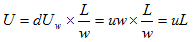

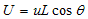
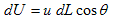
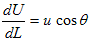 �@�@�@(1)
�@�@�@(1)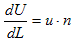
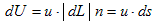
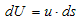 �@�@�@(2)
�@�@�@(2)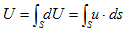 �@�@�@(3)
�@�@�@(3)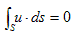 �@�@�@(4)
�@�@�@(4)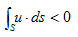
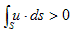
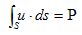
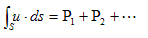

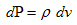 �@�@�@(5)
�@�@�@(5)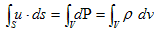 �@�@�@(6)
�@�@�@(6)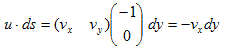
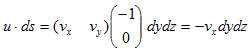

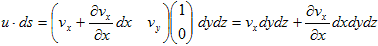
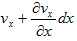
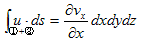
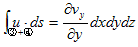
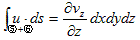
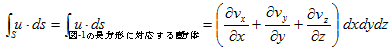
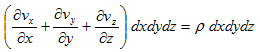
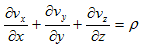 �@�@�@(1)
�@�@�@(1)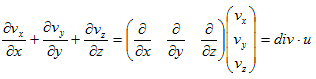
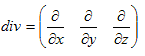
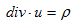 �@�@�@(2)
�@�@�@(2)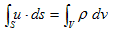
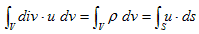
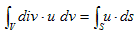 �@�@�@(3)
�@�@�@(3)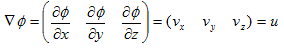 �@�@�@(4)
�@�@�@(4)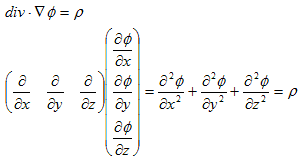 �@�@�@(5)
�@�@�@(5)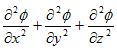
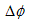
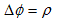 �@�@�@(6)
�@�@�@(6)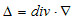 �@�@�@(7)
�@�@�@(7)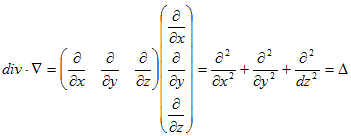 �@�@�@(8)
�@�@�@(8)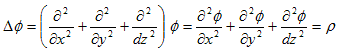
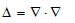 �@�@�@(9)
�@�@�@(9)