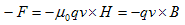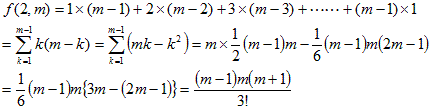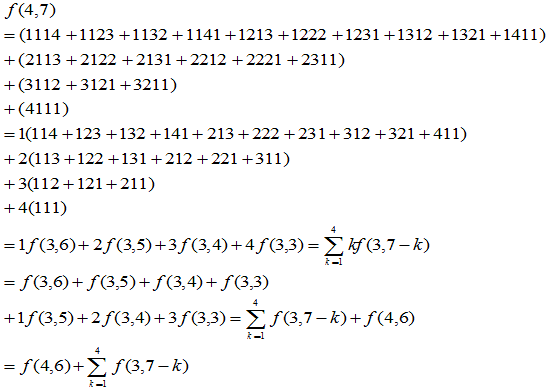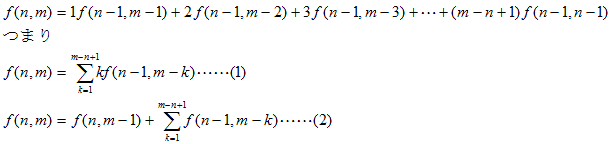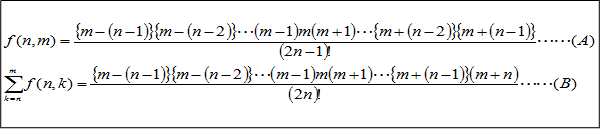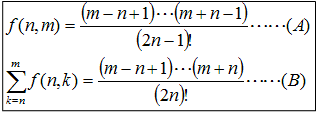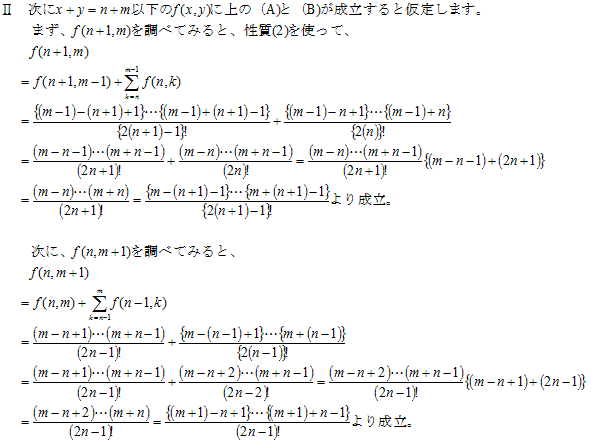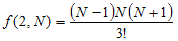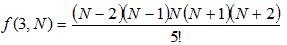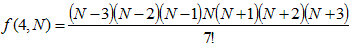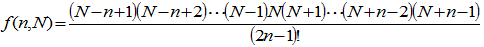NO.1773 コインの出方(2) 2009.2.14. 迷子の雄猫
NO.1771 コインの出方を実験してみました。
結果、試行507017回、出現6337688301回、平均12499.952でした。
最初がox、または最後がxoで終わるとき単独の○と見なすので、12500回より増え
ると思っていたのですが。なんか意外です。
この実験の仕方を補足します。(2009.2.22)
(1)コインを3枚裏、裏、裏の状態で並べておきます。
(2)コインを投げて、列の右側に並べて、一番左側のコインを取り除きます。
(3)並んでいる3枚のコインが裏、表、裏であれば「出現1回」とします。
(4)上記(2),(3)を1セット(10万回)繰り返します。
(5)コインを裏向きに、列の右側に並べて、一番左側のコインを取り除きます。
(6)並んでいる3枚のコインが裏、表、裏であれば「出現1回」とします。
上記の手順で、(1)は、最初表、裏で始まった場合
(5)、(6)は最後裏、表で終わった場合に「出現1回」とするためです。
NO.1772 電磁気学Minimum-4(電磁誘導) 2009.2.12. DDT
以後、ベクトル解析Minimum-1,
2,3,
4の式は、無条件に使います。
1.静電現象の導出
電磁気学Minimum-1,2,
3によれば、磁気現象は
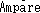 の法則により、
電荷の運動(電気現象)から説明されます。逆に電気現象(電荷の運動)は、
Faradayの電磁誘導の法則により、磁場の変化(磁気現象)から説明されます。
この過程で静磁気現象は、一般の磁気現象から概ね説明出来ました(概ねですが)。
残っているのは、
の法則により、
電荷の運動(電気現象)から説明されます。逆に電気現象(電荷の運動)は、
Faradayの電磁誘導の法則により、磁場の変化(磁気現象)から説明されます。
この過程で静磁気現象は、一般の磁気現象から概ね説明出来ました(概ねですが)。
残っているのは、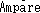 の法則とFaradayの電磁誘導の法則から、静電現象を説明する事です。
これが出来れば電磁気において必要な法則は、
の法則とFaradayの電磁誘導の法則から、静電現象を説明する事です。
これが出来れば電磁気において必要な法則は、
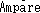 の法則とFaradayの法則、
および関連した保存則だけになります。
の法則とFaradayの法則、
および関連した保存則だけになります。
静電現象において必要な式は、端的に言って次の2つです。
静電現象
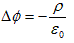 (1)
(1)
φ: 静電ポテンシャル(スカラー),ρ: 電荷密度,ε0: 真空の誘電率.
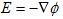 (2)
(2)
E: 静電場の定義.
(1),(2)からはCoulombの法則,静電荷の保存則,ポテンシャル条件、
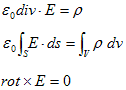
が出てきます。次に、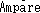 の法則とFaradayの法則は、
の法則とFaradayの法則は、
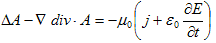 (3)
(3)
A: ベクトルポテンシャル,j: 電流密度,μ0: 真空の透磁率,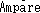 の法則.
の法則.
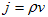 (4)
(4)
j: 電流密度,v:ρの速度,電流密度の定義.
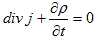 (5)
(5)
電荷の保存則,数学的定義.
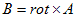 (6)
(6)
B: 磁束密度の定義.
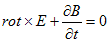 (7)
(7)
Faradayの法則.
となります。
まずFaradayの法則(7)に磁束密度の定義(6)を考慮すると、
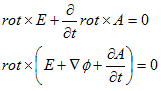
すなわち、
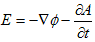 (8)
(8)
が得られます。ここでrot×∇=0を使っています。φは任意のスカラーポテンシャルです。
次に、Δ−∇div・=−rot×rot×と磁束密度の定義(6)を考慮すると、(3)は、
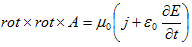
ですが、両辺のdiv をとり、div・rot×=0 および(8)を使うと、
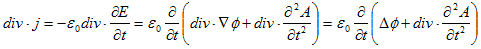 (9)
(9)
が得られます。(9)に数学的定義である(5)を代入すると、
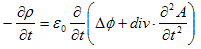
となり、時間tで積分すれば、
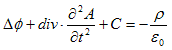 (10)
(10)
です。ここでCは積分常数ですが、(10)の両辺はスカラーでかつ、Cは時間に対する定数なので、C(x,y,z)
とおけます。よってΔCをあらためてCとしても良く、
Δφ+ΔC=Δ(φ+C)をあらためてφとしても良い事になります。
φ→φ+C とする事は、(8)のφについても、それは任意だったので問題ありません。よって(10)は、
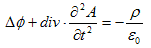 (11)
(11)
となります。静電現象とは、電気単独の現象です。従ってその時、磁束密度Bは、
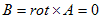 (12)
(12)
になります。このときAには、A+∇ψの不定性がありますが、
rot×Aが0になれば∇ψは何でも良いので、A=0 とおけます。この条件下で(11)と(8)は、
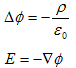
となり、静電現象の基本法則(1)と静電場の定義(2)に一致します。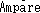 の法則とFaradayの法則から、
静電現象を導けました。
の法則とFaradayの法則から、
静電現象を導けました。
2.Maxwellの方程式
結局1.で使用した式は、(3),(5),(6),(7)で、(4)は使いませんでした。
よく考えれば、(4),(5),(6)は定義であり、必要であればいつでも導けます。
そういうわけで、電磁気現象の本質的な支配方程式、実験とMaxwellの予想によって導かれたものは、
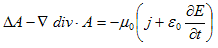 (1)
(1)
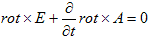 (2)
(2)
と考えられます。ところでFaradayの法則(2)は、さっきやったように、
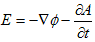 (3)
(3)
とおけて、これにより(2)は自明に満たされます。スカラーポテンシャルφは任意です。
よって(1),(3)を基本方程式とみなす事もできます。さらに(3)を(1)に代入して、基本方程式を一つにできます。
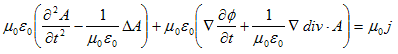 (4)
(4)
(4)でφは任意です。よってφは、
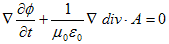 (5)
(5)
を満たすように選べます。(5)を∇について積分する際、∇の積分にはスカラーの積分定数が発生しますが、
それは∂φ/∂tに含める事ができるので、
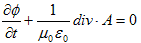 (6)
(6)
と出来ます。(6)のもとで(4)は、
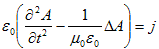 (7)
(7)
ですが、ここでは真空中の電磁場を考えます。
この意味は、真空に電磁場以外ない状態を指しています。
電流密度j があるのは普通は地球上で、考えている解析領域にアンテナがあり、
アンテナを流れる交流電流などが存在する場合です。そうでなければ、j=0 とおけます。
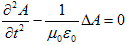 (8)
(8)
(8)を解く事によってAが求まり、(6)からφが決まります。Aとφが決まれば、
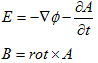
によって、電場Eも磁束密度B(磁場H)も計算できます。
従って、(8)と(6)が真空中の電磁場の支配方程式です。(8)と(6)を以後、Maxwellの電磁場方程式と呼ぶ事にします。
結局、真空中の電磁場の解は(8)が解ければ求まります。偏微分方程式(8)は波動方程式と言われ、
偏微分方程式の中でも形式解が見つかる数少ない例です。数少ない例なので、
(8)を満たす形式解を、以後導いていこうと思いますが、計算が長いので章をあらためます。
3.まとめ
じつは2.(6)の条件を、Lorentzのゲージ条件と言い、
Maxwell方程式のゲージ不変性を表わす一つの表現になっています(詳しくは知りません)。
参考文献には、ゲージ理論の初歩も載っています。
[参考文献]
[1] 現代物理学叢書,電磁力学,牟田泰三,2001年,岩波書店.
NO.1771 コインの出方 2009.2.9. 真夏のサンタ
(2/12 文章差し替え)
ふと考えていて、気になったことがあるので質問させてください。
コインを多くの回数振った時、両端を×ではさまれた、
単独の○は、いくつくらい現れるでしょうか?
例えば、××○×や、○○×○×なら1個、○×○××なら2個、○×○×○なら3個と考えます。
例えば、10万回振った時、そのような○はいくつくらい現れるでしょうか?
10万個のうち、半分が○なので○は5万個。
そのうち、両端が×なのは1/4くらいだとして、12500個くらい?かなとおもうのですが、
実際はどれくらいになるのでしょうか?
NO.1770 行列Aのn乗 2009.2.9. 水の流れ
第220回数学的な応募問題
皆さん、入試問題に行列Aのn乗を求める問題があります。まとめてみました。

注:この記事に関する投稿の掲載は、2009年3月2日以降とします。
NO.1769 極大イデアルと素数(2) 2009.2.9. にちりんシーガイア
イデアルの問題を熟考した結果、私なりの解答が得られましたので、
ご紹介したいと思います。
ある数をmとし、mの倍数の和の集合を(m)とする。
つまり、(m)={rm|r∈Z}である。
これは(m)⊂Zである。
あるイデアルIをおく。
これは、I⊂Z
いま、I≠(0)とする。
するとIは正の整数を含む。
ここでnをIに含まれる最小の正の数とする。
するとI=(n)=(−n)
よって(n)⊂Iが成り立つ。
ここでI=(n)を示すと、
任意の元a∈Iを取ることにすれば(a>0)
a=qn+r (q:商、0以上の整数、r:余り、0≦r<n)
r=a−qn
ここでa∈I、q∈Iより、r∈I
∴r=0(もしr>0ならばnの最小性に矛盾)
∴a=qn∈(n)
∴I⊂(n)が示せた。
次に、(m)⊂(n)⇔mはnの倍数ということを示してみると
m∈(n)、(m)=(−m)よりm=rnと表される。
∴mの倍数はr`m=(r`r)nということになる。
さて(m)⊂Zが極大イデアルであるには
「(m)⊂(n)⊂Z⇔(n)=(m)または(1)=Zである」ことを言えばよい。
いま、m、n>0とする。
「(m)⊂(n)⊂Z⇔(n)=(m)または(1)=Zである」は
(m)⊂(n)⊂Z⇔n=mまたは1 であり
(m)⊂(n)⊂Zとはmがnの倍数であることを表す。
したがって、mの倍数はmまたは1のみである。
∴mは素数である。
これは、題意をしめしたことになる(1:1の対応)。
NO.1768 ジャリズムの数学(2) 2009.2.9. 浜田 明巳
早速ジャリズムの数学に食い付いた生徒がいたので,紹介します.彼によると,2の付く数と2の倍数を除いた自然数の逆数の和は計算出来たが,3の場合が計算出来ない.どうすればよいか,というものでした.
という事で実際に計算してみました.
2の付く数と2の倍数を除いた自然数の逆数の和は,有限?
2の付く数と2の倍数を除いたn桁の自然数の個数を求める.
n=1のとき,1,3,5,7,9の5通り.
n≧2のとき,n桁以下の自然数の個数を求める.
上n−1桁の数はそれぞれ9通りずつ.そのおのおのに対して下1桁の数は1,3,5,7,9の5通り.
n桁の数がすべて0となることはないので,n桁以下の自然数の個数は,9n−1・5
故にn桁の自然数の個数は,9n−1・5−9n−2・5=5・8・9n−2
n桁の自然数の最小値は10n−1であるから,逆数の和は,
5/1+5・8・{1/10+9/102+92/103+………}
=5+40・(1/10)/(1−9/10)
=45
未満である.
3の付く数と3の倍数を除いた自然数の逆数の和は,有限?
3の付く数と3の倍数を除いたn桁の自然数の個数を求める.
n=1のとき,1,2,4,5,7,8の6通り.
n≧2のとき,n桁以下の自然数の個数を求める.
上n−1桁の数はそれぞれ9通りずつ.その和を3で割った余りは0,1,2の3通り.
余りが0のとき,下1桁は1,2,4,5,7,8の6通り.
余りが1のとき,下1桁は0,1,4,6,7,9の6通り.
余りが2のとき,下1桁は0,2,5,6,8,9の6通り.
いずれも6通りとなる.n桁の数がすべて0となることはないので,n桁以下の自然数の個数は,9n−1・6
故にn桁の自然数の個数は,9n−1・6−9n−2・6=6・8・9n−2
n桁の自然数の最小値は10n−1であるから,逆数の和は,
6/1+6・8・{1/10+9/102+92/103+………}
=6+48・(1/10)/(1−9/10)
=54
未満である.
5の付く数と5の倍数を除いた自然数の逆数の和は,有限?
5の付く数と5の倍数を除いたn桁の自然数の個数を求める.
n=1のとき,5の1通り.
n≧2のとき,n桁以下の自然数の個数を求める.
上n−1桁の数はそれぞれ9通りずつ.そのおのおのに対して下1桁の数は0,5の2通り.
n桁の数がすべて0となることはないので,n桁以下の自然数の個数は,9n−1・2
故にn桁の自然数の個数は,9n−1・2−9n−2・2=2・8・9n−2
n桁の自然数の最小値は10n−1であるから,逆数の和は,
1/1+2・8・{1/10+9/102+92/103+………}
=1+16・(1/10)/(1−9/10)
=17
未満である.
ここら辺で力がつきてしまいました.勿論1桁目や2桁目までを根性で正しく計算し,それ以降を上記の方法で計算すれば,もっと正確に評価出来るでしょう.しかしこの問題の趣旨は,面倒くさい分数計算をほとんどせずに有限である事を示そう,というものです.実際上記は整数計算ですよね.こんなものでいいか,と思いま
す.
NO.1767 電磁気学Minimum-3(電磁誘導) 2009.2.9. DDT
以後、ベクトル解析Minimum-1,
2,3,
4の式は、無条件に使います。
1.電磁誘導の法則
実験によれば、磁束密度Bが時間的に変化すると、電場Eは変化します。
電場Eの変化とは、起電力の発生です。この事に最初に気づいたのは、Faraday(ファラデイ)でした。
例えば電場Eが何もなく(E=0)、磁束密度B(磁場H)のみある状況を考えます。
そこでBが時間的に変化すると、同じ場所に電場E≠0が現れます。
E≠0の電場とは荷電粒子に力を及ぼす電場であり、0でない電場は導体中の電子に作用し、
電子の流れ、すなわち電流が生じます。よって電場Eの変化とは、起電力の発生です。
その法則は、電場Eと磁束密度Bによって記述できます。
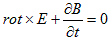 (1)
(1)
(1)をFaradayの電磁誘導の法則と言い、実験的に得られた(1)の原型は、
次のようにしてたどる事ができます。まず(1)を、ある曲面Sで積分すると、
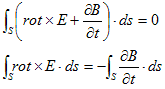 (2)
(2)
となり、(2)の左辺は、Stokesの定理から、
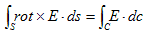 (3)
(3)
です。ここでCは曲面Sの境界で空間内の閉曲線、dc はその接線ベクトルです。
Cは、閉じた電気回路とみなせます。何故ならCに沿って電場Eを積分すれば、
Cに沿った静電ポテンシャルφを定義するのとほぼ同じです。
ただし、このφはCに固有のもので(経路依存で)、全空間に対する通常の静電ポテンシャルとは違います。
何故なら、rot×E≠0 だからです。それでもCだけに話を限れば、次のように言えます。
静電ポテンシャルφの次元はJ/Cです。もし回路C内に荷電粒子q(C)があり、
電場E=dφ/dcの作用によって、Cに沿って測った位置p1からp2に移動したとすれば、
荷電粒子qは φ(p2)−φ(p1) (J) だけのエネルギーを得ます。
これは、Cに電圧がかかっているのと同じです。(3)と(2)をつなげる事により、それが、
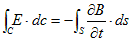 (4)
(4)
で与えられるという事は、回路Cの面積で囲まれた磁束密度の変化速度の合計は、
その回路C上に電圧を発生させる(起電力が発生する)。
これが、実験的に得られたFaradayの電磁誘導の法則です。
逆に(4)を認めれば、(4),(3),(2)とたどる事により、(2)でSを任意に小さくとれる事にも注意して、
(1)に戻れます。
2.Lorents力
電磁誘導の法則を使うと、運動する荷電粒子が、周囲磁場から受ける力を計算できます。
電荷qを持つ荷電粒子が、速度vで運動しているとします。
速度vは、線素vdtを定義します。vdtと独立な方向に線素dcを考えると、
vdtとdcは面素ds=vdt×dcを定義します。dsの位置での磁束密度をBとすると、dsを横切る磁束密度の合計は、
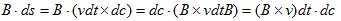 (1)
(1)
となります。ただし外積の公式、
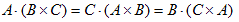
を使っています。従って(1)の両辺をdtで割れば、
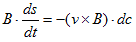 (2)
(2)
が得られます。(2)の左辺は、一定の磁束密度に面積の変化率をかけたものになりますが、面積は変化せず、
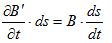 (3)
(3)
を満たす磁束密度B'が、∂B'/∂tで変化したものと考える事もできます。
このように考えれば、1.(4)より電場、
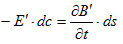
が発生する事になり、これに(2)を合わせると、
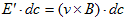
すなわち、
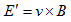
が得られます。電場E'の中に置かれた荷電粒子qは、電場E'からの力、
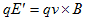
を受け、E'のほかに最初から、電場Eもあったとすれば、
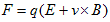
の力を受けます。これをLorents力と言います。もちろんLorents(ローレンツ)さんが導いたからです。
ところで以上の話に、どこか妙な引っ掛かりは感じないでしょうか?。これについては再論します。
3.Lorents力再び
ところが、Ampa(_)reの法則からもLorents力を計算できるのです。
ここで周囲磁場は、静磁気のCoulombの法則で与えられるものです。
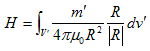 (1)
(1)
ここで磁荷密度m'は、巨視的現象として現象論的に考えられるものです。
一方速度vで運動する荷電粒子の電荷をqとすれば、それは定常な電流素qvδdv を定義します。
qvδdv による磁場はAmpa(_)reの法則より、
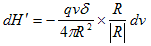 (2)
(2)
になります。ここでdv は、荷電粒子の位置の微小体積なので、Rの方向がdH'の作用方向の逆となり、
−符号が付きます。(2)による、磁荷密度m'全体への合力は、
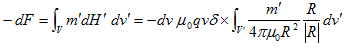 (3)
(3)
と計算できますが、(1)より、(3)の右辺の積分項はHに等しいので、
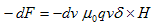 (4)
(4)
が得られます。さらに(4)を、dv を含むような任意の体積で積分すれば、δ関数の性質から、
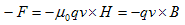
となります。最後に作用反作用の法則により、荷電粒子qは、−Fと逆向きの力Fを受けるはずなので、
磁場Hの中を速度vで運動する荷電粒子qは、電場Eもあるとすれば、
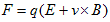
の力を受けます。またLorents力が出てきました。しかしこの話も何か、きな臭くないですか?。
4.荷電粒子が動くのか?、磁場が動くのか?
2.と3.で行った、Lorents力の計算の構図をまとめてみます。
2.では、運動する荷電粒子が周囲磁場から受ける力を計算すると言いながら、
実際には磁場の方を動かして、荷電粒子への力を直接計算します。
3.では、運動する荷電粒子が周囲磁場から受ける力を計算すると言いながら、
実際には動く荷電粒子が周囲へ及ぼす力から、間接的に荷電粒子への力を計算します。
こうやって並べてみると、2.と3.のやり方には妙な対称性まであり、
しかもどっちも素直ではありません。何か本質的な事を見逃している気がしてきます。
例えば2.のような事になったのは、磁場が変化しようと、磁場の中を荷電粒子が運動しようと、
荷電粒子にとっては、どちらも磁場の変化であるという形に、
電磁誘導の法則がなっていないからだとも言えます。
しかし古典的電磁気学の範囲では、これ以上の事はできないようなのです。
妙な対称性を、ちゃんとした対称性(相対性)に直すには、特殊相対性理論が必要らしいとだけ、
ここでは言います。
5.まとめ
電磁気学Minimum-1,2,3によって、電磁場を導くのに必要な法則は、全て出揃いましたが、
今回一番気になったのは、やはり2.と3.の関係です。少々深読みしすぎかもしれませんが、
この辺りの事情に関しても参考文献には、ちゃんと読めば関連する事が書いてあります
(でもまだ、ちゃんと読んでません)。
[参考文献]
[1] 現代物理学叢書,電磁力学,牟田泰三,2001年,岩波書店.
NO.1766 自然数の積の和(2) 2009.2.9. 夜ふかしのつらいおじさん
f(n,m)を、和がmとなるn個の自然数の積の総和とします。(n≦m)
f(n,m)は、nHm-n個の積の総和となります。
例えば、
f(1,1)=1, f(1,m)=m
f(2,2)=1×1=1,
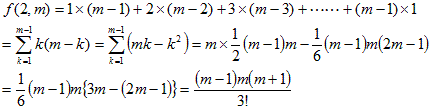
です。
少し具体的な例を見てみます。
数と数の間の掛け算記号「×」は省略します。
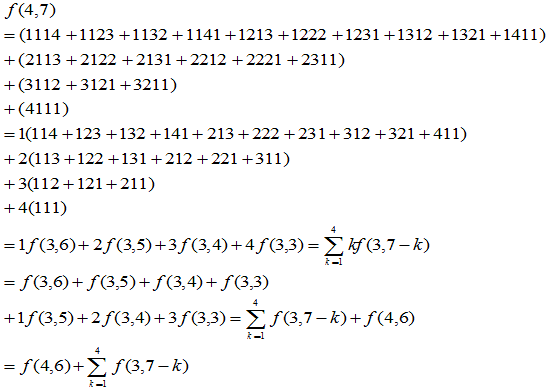
以上から次の性質が確認できます。
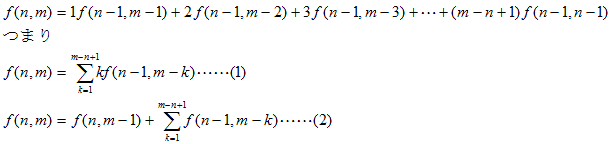
さて、f(x,y)には次の関係成立することを示します。
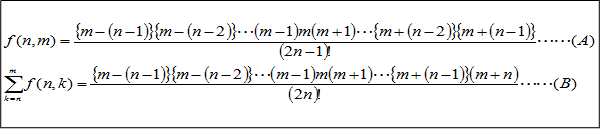
これを次のように略記します。
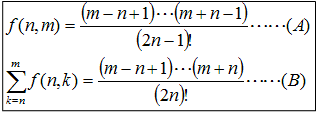

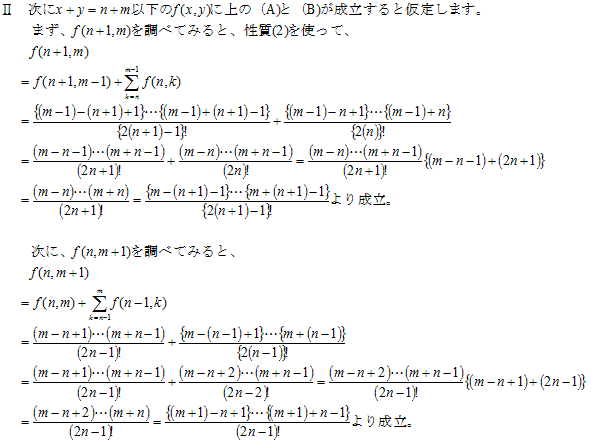
以上から
問題1
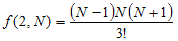
問題2
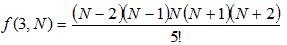
問題3
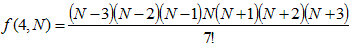
問題4
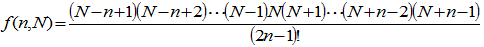
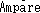 の法則により、
電荷の運動(電気現象)から説明されます。逆に電気現象(電荷の運動)は、
Faradayの電磁誘導の法則により、磁場の変化(磁気現象)から説明されます。
この過程で静磁気現象は、一般の磁気現象から概ね説明出来ました(概ねですが)。
残っているのは、
の法則により、
電荷の運動(電気現象)から説明されます。逆に電気現象(電荷の運動)は、
Faradayの電磁誘導の法則により、磁場の変化(磁気現象)から説明されます。
この過程で静磁気現象は、一般の磁気現象から概ね説明出来ました(概ねですが)。
残っているのは、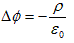 (1)
(1)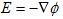 (2)
(2)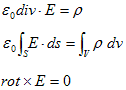
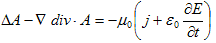 (3)
(3)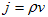 (4)
(4)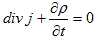 (5)
(5)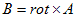 (6)
(6)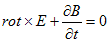 (7)
(7)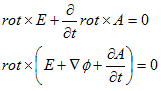
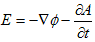 (8)
(8)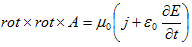
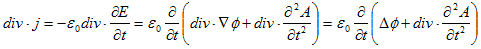 (9)
(9)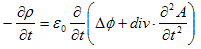
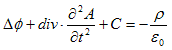 (10)
(10)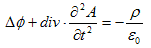 (11)
(11)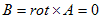 (12)
(12)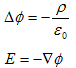
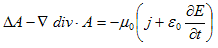 (1)
(1)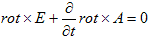 (2)
(2)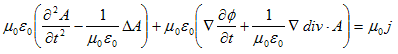 (4)
(4)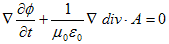 (5)
(5)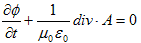 (6)
(6)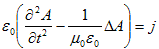 (7)
(7)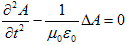 (8)
(8)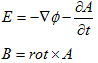

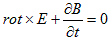 (1)
(1)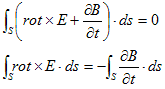 (2)
(2)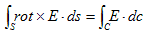 (3)
(3)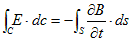 (4)
(4)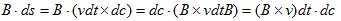 (1)
(1)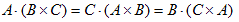
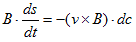 (2)
(2)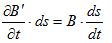 (3)
(3)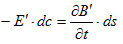
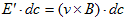
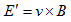
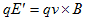
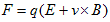
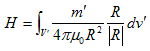 (1)
(1)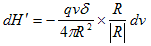 (2)
(2)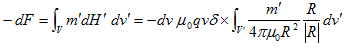 (3)
(3)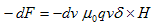 (4)
(4)