ColloquiumNO.238
|
皆さん。バームクーヘン積分をご存知ですか。ある図形をｙ軸の周りに回転させてできる回転体の体積を求めるのに便利な公式です。ここで、今年の滋賀県立大学前期の問題を一部か改題して紹介します。
この問題を解くにあたって、バームクーヘン積分を参考にしても構いません。
注：この記事に関する投稿の掲載は、2009年１月 日以降とします。
ベクトル解析Minimum-1，2，
3の続きです。
Minimum-3で、ポテンシャルφと∇とdiv に関連して、rot を導入しましたが、その定義はかなり形式的なものでした。ここではrot に、もっと具体的な物理的イメージを与えます。再び流体力学を利用します。
章番は、ベクトル解析Minimum-3を引き継ぎます。以前の結果を参照する場合は、V-1.3.(6)，V-2.5.(11)などと書きます。
７．Stocksの定理、divとrotの関係
uを流体（水）の流速として、
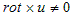
のとき、uを導く速度ポテンシャルφは存在しない、がV-3.6.の結果でした。rot×u＝0 の場合と、≠0 の場合の違いをつかむためには、次のような例で考えれば十分です。最初に、速度ポテンシャルがある場合（rot×u＝0 の場合）で考えます。
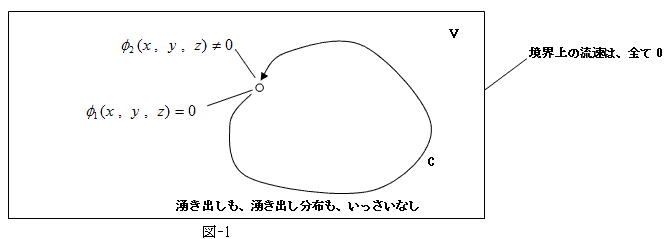
図-1にように、体積Ｖの境界上で水の出入りはなく、内部には一つの蛇口もない場合を考えます。これは死水（止まった水）だと考えられます。実際このときの速度ポテンシャルφは、
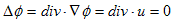
で、境界上で全ての流速0という境界条件を持つ、ラプラス方程式、
の解は、φ＝0となり、Ｖの任意点での流速も、
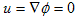
です。
ところが、V-3.6.で述べたように、
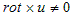
の場合、φの増分は経路依存になるので、図-1のように経路Cに沿ってφの増分を取った場合、たとえ点(x，y，z) を出発したとき、φ1＝0 であっても、戻って来た時にはφ2≠0 かもしれません。これもV-3.6.でやったように、
なので、φ2−φ1≠0 という事は、経路C上に生きた水（動いている水）があるという事です。何故なら全ての点でu＝0 なら、φ2−φ1＝0 は明らかだからです。従って、rot×u≠0 の場合は、たとえ境界上での水の出入りがなく、内部に湧き出しがない場合でも、流れが存在しうる事になります。この流れとは、どのようなものでしょう？。そこで、流体のある一点（微小要素）の動きを、時間に沿って追跡します。
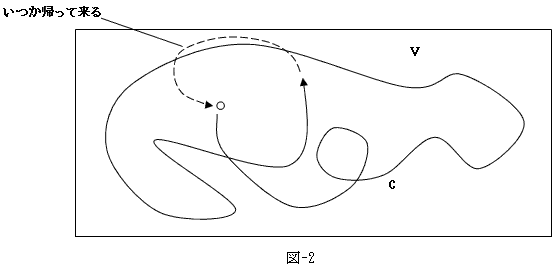
一点の動きを、時間に従って追跡した軌跡とは、その点（粒子）の軌道ですが、流体力学では流線と言われます。この流線は、体積Ｖの中でどのように流れるかわかりませんが、とにかくＶを出ない事だけは確かです。
何故ならＶの境界を横切った瞬間、そこの境界上の流速は0でなくなるからです。よって体積Ｖ中の流れは全て、有界領域に閉じ込められた粒子の運動です。
流体力学における運動方程式、V-1.2.(1)、
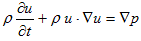
は、じつはNewtonの運動方程式の言い換えです。従って図-2に対しても、有界領域に閉じ込められた粒子の力学系の一般的な結果を適用できます。それがポアンカレの再帰定理「有界領域に閉じ込められた粒子の運動は、いつかその出発点に戻って来る」です。これが図-1に存在しうる流れの、一般的な性質です。この証明には、粒子の運動は微分方程式によって記述されるという仮定と、体積Ｖが有限であるという事実しか使われません。よってrot×u≠0 の場合、そこには一般的に、循環する流れが存在する事になります。循環する流れの事を、渦と呼びます。それで、
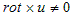
のとき、渦あり流れ、
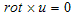
のとき、渦なし流れと言います（渦なし流れは、速度ポテンシャルで記述できます）。渦の強さを定義します。
図-2に示した経路C上での線積分、
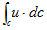(1)
は、渦の流線に沿った積分なので、uとdcは常に平行です。従ってこれは、循環上で動いている水の総量である、渦の流量になるので、これによって渦の強さを定義できます。渦の流量の事を、あらためて循環と定義します。
しかし、図-1のような状態でももう、Ｖの各点の流速は0と限らない事を知っています。そうであるならば、循環は渦の流線に沿わなくても定義できます。まさに(1)を用い、循環Γを、
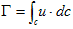(2)
で定義します。これは任意に取った閉経路C上に流れているとみなせる渦の強さであり、uとdcは、もはや常に平行ではありません。ところが(2)は、変形されたGaussの発散定理とみなす事が出来きます。
とりあえず2次元で考えて、閉経路Cの線素ベクトル（それはCの外法線方向を向くものですが）は、
と表わせます。ここで、
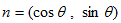
は、曲線Cの外法線方向単位ベクトルであり、dLはCの線素です。Cの接線ベクトルdc は、ds に左回りに直行するベクトルです。
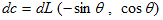
そういうわけで、(2)のu･dc は
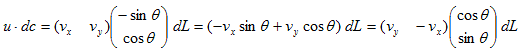
と書き換え可能です。この結果を使うと、
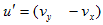
として、
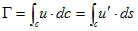
となります。2次元のGaussの発散定理を適用すれば、
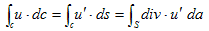(3)
です。
ここにda は、考えている平面の面素であり、ＳはCで囲まれる面積です。そしてdiv･u' は、
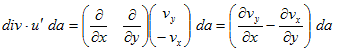(4)
になりますが、(3)の最右辺のような積分を扱う場合、(4)で面素da そのものを扱うより、面素ベクトルds で扱った方が便利である事が知られています。そこで(4)のda を、面素ベクトルds に書き換えます。いまは平面なので、面素ベクトルは、
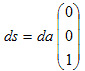
です。これを使って(4)を書き直すと、
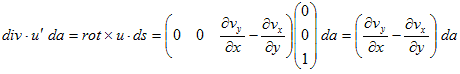(5)
となります。3次元空間の中の一般的な曲面Ｓに関しても、曲面を局所的に微小平面と考え、微小平面に接するような座標系で考えてやれば、やはり(5)の状況が成り立ちます。この時は、流れも3次元的になるので、もはや(5)のrot×u の第1，第2成分は0ではありませんが、結果は変わりません。
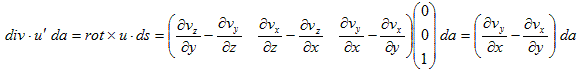(6)
ところで(6)は、2次元のGaussの発散定理(3)から導かれた形で、それをdiv･u' da＝rot×u･ds が示します。よって、本来のGaussの発散定理でρを湧き出し密度として、ρda＝div･u da が各点の微小な湧き出しを表わしていたように、
も形式的には、各点での微小な、一種の湧き出しを表わすと考えられます。γ（ベクトルです）を渦度と呼び、渦の発生密度を表わすものと解釈できます。発生と言う意味での湧き出しです。rot×u･ds を一種の湧き出しと捉えると、2次元のGaussの発散定理(3)は、この場合も2次元的に、そのまま成り立つはずなので、(3)でdiv･u' da＝rot×u･ds と置き換え、
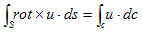(7)
が得られます。これをStocksの定理と言います。
循環Γ、
(8)
にも保存則があります。Γは、ある曲面上の渦度分布から発生する、曲面周上の渦の強さを表わすものだと言えます。曲面Ｓが閉じている場合、(8)の最右辺の積分は図-3のように、2つに分けて考えますが、切り口の境界の積分方向は、図に示したように逆向きになります。従って、(8)の最右辺の積分は、
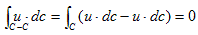
となって、常に0です。これより、
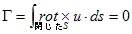(9)
となります。この事を、閉曲面上の渦は、増えたり減ったりしないと言います。
(9)に、3次元のGaussの発散定理を使うと、関連したベクトル解析の公式を得ます。
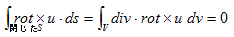(10)
(10)で、体積Ｖは任意に小さく出来るので、div･rot×u dv＝0、すなわち、
(11)
を得ます。実際、成分で計算すると、
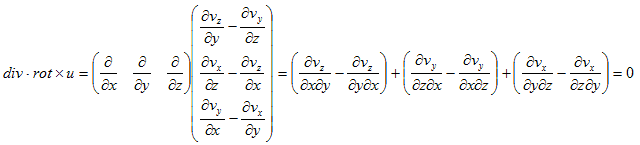(12)
となるので、(9)は恒等式です。上記では、速度の各成分に対して偏微分の順序交換を使っていますが、これは問題ありません。
渦あり流れの場合、速度ポテンシャルφを想定しても、φには偏微分の順序交換が成り立たないの意味は、φはポテンシャルにならないというだけの意味であり、(x，y，z，t) のスカラー関数としてのvx，vy，vz に、偏微分の順序交換が使えないわけではありません。(x，y，z，t) によって、vx，vy，vz の値は完全に定まるので、(x，y，z，t) のスカラー関数vx，vy，vz には、いつでも偏微分の順序交換は使えます。
(12)の偏微分の順序交換によって0になる部分を見ると、分子にはいつも同じ速度成分が来ています。ここから(12)を略記して、
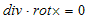(13)
と書くのが習慣ですが、何の説明もなく、div rot＝0と書かれる事も多いです。
最後に、これからよく利用するようになる公式をあげます。それはa，b，c を普通のベクトルとして、外積における公式、
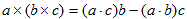(14)
に関連したものです。これまでベクトル解析Minimum-1，
2，
3を通じて、微分作用素∇，div，rot，Δを紹介してきましたが、それらの実体はみな∇でした。
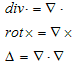
そこで、(14)に関連して、
(15)
が考えられます。ここでＡ＝(Ａx，Ａy，Ａz) は普通のベクトルです。(15)の成分順序並びは確かに正しいのですが、微分作用素がからむ場合、少し注意が必要です。微分作用素の積は、微分演算をあたかも普通の積とみなして、
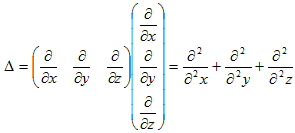
などとやりますが、例えば一つの微分作用素∂/∂x においても、それが関数の積fgに作用する場合には、
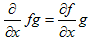
なのか、
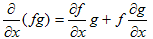
なのか、という問題が生じます。極座標などに∇を変換すると、このような事はよく起こります。また(12)のように成分が混ざり、成分ごとの確認が必要な時もあります。
いま微分される関数Ａは一つなので、積の微分の心配はありません。(15)の右辺は、成分を混ぜるものではないので、(12)のようにもなりません。すると問題になるのは、1項目に関しては、(∇･Ａ)と∇が交換可能か？、という事です。(∇･Ａ)はスカラー，∇はベクトルなので、これは問題ありません。同様に2項目も交換可能で、スカラー作用素(∇･∇) が、スカラー的にベクトルＡに作用するという事なので、これも問題ありません。よって(15)を通常の記法で書き直せば、
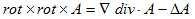
となりますが、略記して、
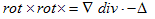(16)
です。もう一つは、まさに積の微分公式に関連するもので、スカラーkとベクトルＡに関する、
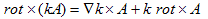(17)
というものです。これはもう、成分は混ざるし積は関係するしなので、恐らく直接確かめるのが一番の早道と思われます。まずrot を普通のベクトルと考えると、rot×(kＡ)＝k rot×Ａ なので、(17)の2項目が出てきます。1項目は積の微分の影響です。1項目については、Ａを定数と考えれば良いので、
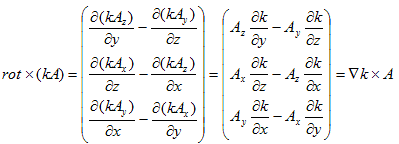
となり、(17)が成り立ちます。
皆さん、今年、早稲田と芝浦工業の入試問題に斜回転体の体積を求める問題がでていました。一部改題して出題します。
この問題を解くにあたってコロキウム室にあるテーマ別で円に関する微分を参考にしても構いません。
注：この記事に関する投稿の掲載は、２００８年12月29日以降とします。
● ２次関数 ｙ＝ａｘ2＋ｂｘ＋ｃ は、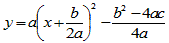 
と変形できるので、
軸の式は、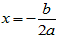 
です。
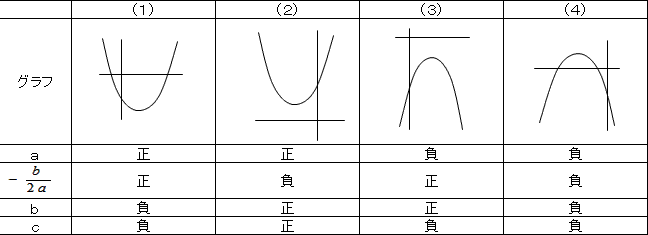
係数の符号は、ａは放物線の開き方、ｂは軸の位置とａの符号、ｃはｙ切片で決まります。
問題１
● ３次関数 ｙ＝ａｘ3＋ｂｘ2＋ｃｘ＋ｄ の導関数は、ｙ’＝３ａｘ2＋２ｂｘ＋ｃ です。
係数の符号は、ａはグラフの形（ｘ→∞で右上がりは正）、ｄはｙ切片で決まります。
ｂとｃの符号は、導関数のグラフで分かります。
（導関数のグラフは元の関数のグラフの極値のところがｘ軸との交点になります）
導関数の軸の式は、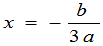 
です。
問題２
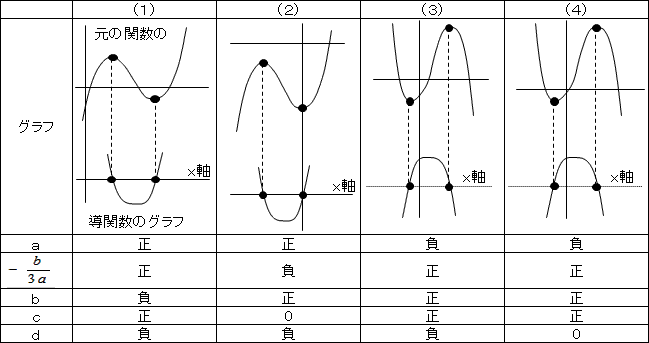
問題３
（１） ｆ（ｘ）＝ｘ3＋ａｘ2＋ｂｘ＋ｃ の導関数は
f’(ｘ)＝3ｘ2＋2ａｘ＋ｂ＝(ｘ−１)(３ｘ−ｂ)＝３ｘ2−(ｂ＋３)ｘ＋ｂ です。
ｘ＝ｂ／３ で極小値をとらなくてはならないので、ｂ／３＞１、つまり、ｂ＞３ です。
また、導関数の式をみて ２ａ＝−(ｂ＋３)
∴２ａ＋ｂ＋３＝０ (ｂ＞３) です。
（２） ｘ＝−２で極小値をとるので、
ｆ（ｘ）＝ｘ3＋ａｘ２＋ｂｘ＋ｃ の導関数は
f’(ｘ)＝3ｘ2＋2ａｘ＋ｂ＝(ｘ＋２)(３ｘ＋ｂ／２)＝３ｘ2＋(ｂ／２＋６)ｘ＋ｂ です。
ｘ＝−ｂ／６ で極大値をとらなくてはならないので、−ｂ／６＜−２、つまり、ｂ＞１２ です。
また、導関数の式をみて ２ａ＝ｂ／２＋６
∴４ａ−ｂ−１２＝０ (ｂ＞１２) です。
● f(X)=f(0)+f'(0)X+f''(0)/2!X2+f'''(0)/3!X3+f''''(0)/4!X4+･･･
問題４
（１） f(0)=1 , f'(0)=1 , f''(0)=2 , f'''(0)=6 を上の式に代入すると、
f(X)=１+１X+２/2!X2+６/3!X3+f''''(0)/4!X4+･･･
=１＋Ｘ＋Ｘ2＋Ｘ3＋・・・
（２） f(0)=1 , f'(0)=1 , f''(0)=1 , f'''(0)=1 , f''''(0)=1 ・・・を上の式に代入すると、
f(X)=１+１X+１/2!X2+１/3!X3+１/4!X4+･･･
( =ｅx )
（３） f(0)=0 , f'(0)=1 , f''(0)=0 , f'''(0)=-1 , f''''(0)=0 ・・・を上の式に代入すると、
f(X)=１X-１/3!X3+１/5!X5+ ･･･
( =sin X )
（４） f(0)=1 , f'(0)=0 , f''(0)=-1 , f'''(0)=0 , f''''(0)=1 ・・・を上の式に代入すると、
f(X)=１-１/2!X2+１/4!X4- ･･･
( =cos X )
問題５
ｅiθの導関数は、(ｅiθ)(n)＝inｅiθ より、マクローリン展開は
ｅiθ＝１＋ｉθ−１／2！θ2−ｉ／3！θ3＋１／4！θ4＋i／5！θ5＋・・・
(cos θ＋ｉsin θ)’＝−sin θ＋ｉcos θ
(cos θ＋ｉsin θ)’’＝−cos θ−ｉsin θ
(cos θ＋ｉsin θ)’’’＝sin θ−ｉcos θ
(cos θ＋ｉsin θ)(4)＝cos θ＋ｉsin θ
(cos θ＋ｉsin θ)(5)＝−sin θ＋ｉcos θ
より、(cos θ＋ｉsin θ) のマクローリン展開は
cos θ＋ｉsin θ＝１＋ｉθ−１／2！θ2−ｉ／3！θ3＋１／4！θ4＋・・・
よりそれぞれのマクローリン展開が同じになります。
問題６
ｅｉπ＝cos π＋ｉ sin π＝−１
問題７
ｅiθ＝cos θ＋ｉ sin θ において、θ＝π／2 のとき、右辺の値が ｉ になります。
つまり ｅｉπ／2＝ｉ
両辺を ｉ 乗すると
( ｅｉπ／2)ｉ＝ｉｉ
ｅ-π／2＝ｉｉ
エクセルの関数を利用して
ｅ-π／2＝0.207879576350762･･･
が求められます。
問題４の（２）において、X＝−π／2 として計算すればよいのですが、収束が遅いです。
| 1項まで | 2項まで | 3項まで | 4項まで | 5項まで | 6項まで | 7項まで | 8項まで | 9項まで | 10項まで | ・・・ |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.5708 | 0.662904 | 0.01694 | 0.27061 | 0.190917 | 0.21178 | 0.207099 | 0.208018 | 0.207858 | ・・・ |
１°
(1＋１／n）ｎ → ｅ (ｎ→∞) は大前提とします。
２°
(1−１／n）−ｎ → ｅ (ｎ→∞) も簡単な変形で確認できます。
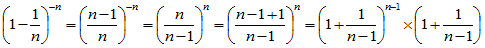
３°
上の１°、２°より、
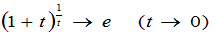
（ｔは正で０に近づいても、負で０に近づいても問題ありません）
４°
ｉ を虚数単位として、
(1＋１／i n）i ｎ → ｅ (ｎ→∞)
５°
ｉ を虚数単位として、
(1−１／i n）−i ｎ → ｅ (ｎ→∞)
６°
上の４°、５°より、
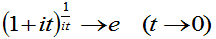
（ｔは正で０に近づいても、負で０に近づいても問題ありません）
※ ４°、５°、６°は自分では確認できていないのですが認めることにします。
７°
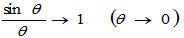
８°
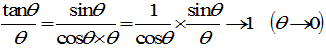
問題８
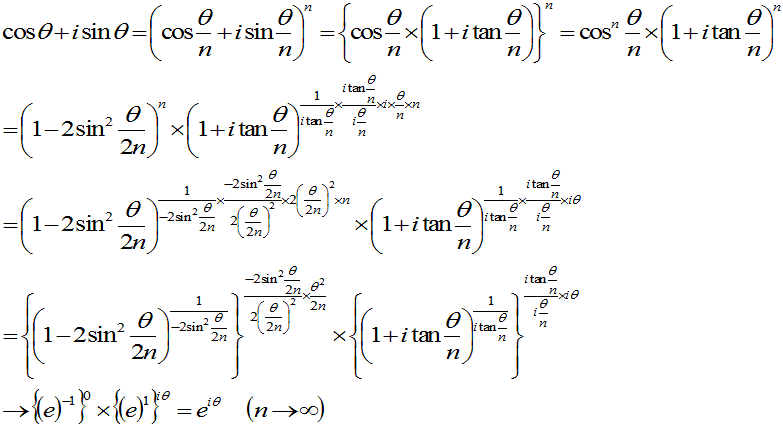
以後、ベクトル解析Minimum-1，2，
3の式は、無条件に使います。
静電現象は、静止した電荷と電荷の間に働く力を扱います。そこでの目的は、時間的に変化しない電荷分布が与えられた時に、各電荷に働く力を知る事です。ここで時間的に変化しないとは、運動はもちろんしないし、静止していても時間的に脈動する事もない、という意味です。要するに静電気です。
１．電場の概念
経験的に電荷（電気量を持つ物体）の存在はわかっています。電荷は連続的に分布するように見える時もありますが、その実体は電子の持つ素電荷で、離散的です。電子は点粒子と呼ばれるほど小さいので、その理想化として、一定の電荷（電気量）が一点に集中した点電荷の概念が得られます。
点電荷に対する実験結果がCoulombの法則です。
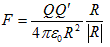(1)
(1)で、ＱとＱ'は、位置ベクトルrとr'にある点電荷で、Ｒ＝r−r'です。ε0は、真空の誘電率と呼ばれる定数で、ＦはＱとＱ'の間に働く力です。もちろん実際には、実験系のスケールに対して十分小さな帯電球（もちろん動いてない）などを用意します。
電気力は重力などとは違う力なので、電荷は新しい力の発生源とみなせます。従って、力Ｆや距離Ｒの単位の組み合わせで電荷の単位を定義できません。電荷に対して新しい単位C（クーロン）を導入します。ただしCの規格化、つまり何を1C とするかは任意に出来ます。それが、
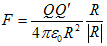(2)
の定義です。(2)より、誘電率の単位と値（実験による）が決まります。
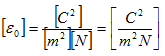
電荷には符号のある事がわかっています。(1)のＦをＱ'がＱに及ぼす力とみなすと、ベクトルＲの方向より、ＱとＱ'が同符号なら斥力，異符号なら引力です。
ところで、(1)のＦをＱ'がＱに及ぼす力とみなすとは、電荷Ｑ'を力の発生源とみなすのと同じです。力とは相互作用です。そうするとＱ'は作用の発生源だとも言えます。Ｑ'が作用の発生源であるならば、その作用は、Ｑ'の性質だけで規定されるのが望ましいと思えます。しかし(1)の力Ｆは、作用する先の電荷Ｑにも影響されます。そこで(1)をＱで規格化し、Ｑ'の性質だけで規定される作用を定義します。
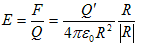(3)
(3)のＥを、Ｑ'による電場と呼びます。電場の概念のもとでの相互作用のイメージは、次のようなものです。
最初に電荷Ｑ'が全空間に、作用の場Ｅを準備します。そこにたまたま電荷Ｑが迷い込むと、電荷量に応じてＱが応答し、相互作用Ｆが成立するという構図です。
ＱもＱ'も静止している場合、電場Ｅを用いるか、Coulomb力Ｆを用いるかは、考え方の違いに過ぎません。しかし変動する電気現象を扱うようになると、Coulombの法則は成り立ちませんが、電場の概念は有効です。
電場の単位は明らかに、
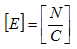
です。
２．静電ポテンシャルと電場
1.(3)で定義される電場があれば、2つの点電荷の間の静電現象は十分に記述できます。(3)は、Coulombの法則から出てきました。Coulombの法則を含むような静電現象の法則は、静電ポテンシャルφと電荷密度ρを用いて記述できます。
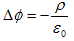(1)
(1)のε0は、真空の誘電率と呼ばれる定数で、1.で述べたように、その値はCoulombの法則を通じて実験的に定まり、
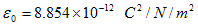
という値になります。一方、電荷密度ρの単位は、
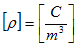
で、ρは空間的に連続して分布するとみなします。電荷の実体が、電子の持つ離散的な素電荷である事を考えると、電荷密度ρを連続分布とみなせるかどうかは、電子の持つ素電荷の大きさによります。実験によりその値eは、
e=1.602×10-19Ｃ
という大変小さなものです。よって、ある体積中に沢山の電子が分布するとき（ふつう沢山あります）、その平均化として、電荷密度ρの考えは妥当なものになります。また静電ポテンシャルφの次元は、
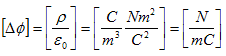
なので、
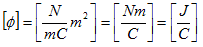
です。
ここでは、点電荷の電場1.(3)を、(1)から導き、逆に点電荷の電場があれば、(1)に戻れる事を示します。最初に、ベクトル解析の公式、
に注意して、電場Ｅを、
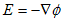(2)
で定義すると(1)は、
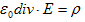(3)
と書き直せます。(3)の方を、Coulombの法則と呼ぶ事にして、1.(3)の方は以後、点電荷に対するCoulombの法則と言う事にします。(2)による電場Ｅの単位は、静電ポテンシャルの次元より、
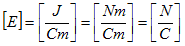
となり、1.(3)による電場の単位と一致します。(3)を満たす電場(2)の事を、静電場と言います。
３．静電荷の保存則
2.(3)は、Gaussの発散定理を用いて積分できます。まず左辺は、
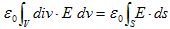
となります。ここでＶは、2.(1)の電荷密度ρの存在範囲を全て覆うもので、ＳはＶの境界，dsはＳの面素ベクトルを表わすものとします。右辺にも同じ積分をすれば、
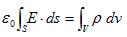(1)
が得られます。
(1)は、ある体積中の電荷密度の合計（電荷）は、その体積の表面から流れ出す電場（ベクトル）の合計で測れる事を言っています。これを静電荷の保存則と言う事にします。
４．Coulombの法則から、点電荷のCoulombの法則へ
電荷密度とは、ある体積中に存在する多数の電子群の分布を平均化して、便宜的に連続量ρ(x，y，z)で表わしたものでした。この近似において一個の電子を考えます。電子の半径は非常に小さいので、これの理想化として、拡がりを持たない電荷、すなわち点電荷の概念が再び得られます。
電荷密度の観点からは点電荷とは（電子のように）、空間の一点に有限の電気量が集中したものと考える事ができます。電荷密度の言葉で言うと、これはディラックのデルタ関数をδ，位置r'にある点電荷の電荷をＱ'(r')として、ρ＝Ｑ'δ(r−r') になるのと同じです。
δ関数とラプラシアンΔに関しては、ラプラス方程式の基本解として、
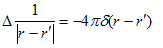(1)
が成り立っていました。ここでΔは、rに作用します。
そこで、
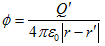(2)
とおけば、
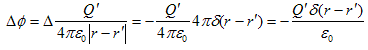
となり、(2)は2.(1)を満たす事がわかります。よって、点電荷の静電ポテンシャルは、
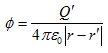
です。ここから定義2.(2)に従って、点電荷Ｑ'の静電場は、
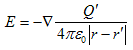(3)
となります。この∇も、rに作用するものです。何故なら、
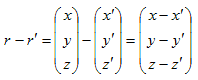
であり、(x'，y'，z')は点電荷の位置（δ関数の特異点）を表わす固定値なので、∇はr＝(x，y，z)にしか作用しません。従って、
r-r'=R
とすれば、
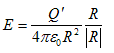(4)
が得られます。これが、点電荷Ｑ'に対して実験的に確認できる、Coulombの法則でした。
５．点電荷のCoulombの法則からCoulombの法則へ
逆に関係式4.(4)のもとに、電荷密度ρを用いて、微小な点電荷、
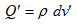
を導入する事を考えます。ここでdv' は、位置r'にある微小な体積要素です。これによって、4.(4)から発生する電場も微小なので、それをdＥと書きます。
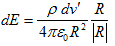(1)
です。(1)は、位置r'＝(x'，y'，z') にある微小な点電荷ρdv' によって、任意の位置r＝(x，y，z) に発生する電場を表わしています。
実験的に、電場は重ね合わせ出来る事がわかっています。従って電荷密度ρが連続的に分布する場合、分布全体から発生する電場Ｅを求めるには、各点のρが、同じ位置r＝(x，y，z) に発生させる電場dＥを、合計すれば良い事になります。
ρを全て含む体積をＶとすれば、
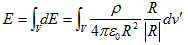(2)
が得られます。4.(3)，(4)より、(2)の最右辺はさらに、
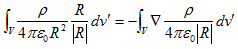
と変形できるので、
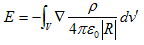(3)
です。(3)の右辺の被積分関数をfとすると、f(r，r') ですが、積分はr'に関するものなので、積分後はr'はなくなり、rのみの関数になります。従ってＥは、rの関数です。そこで、rに作用するdiv を用いて、
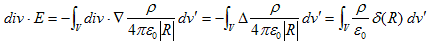
と書けます。div が積分記号を通過できるのは、積分はr' に関するもので、rに作用するdiv と無関係だからです（積分記号下の微分）。div･∇＝Δは、4.(3)より、∇もrに作用するので、ベクトル解析の公式です。最後の項には、4.(1)を使っています。さらに最後の項にδ関数の性質を使いますが、位置r は任意なので、その際にr∈Ｖとします。最後の項を詳しく書くと、
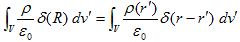(4)
です。δ関数の性質より、
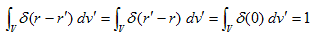(5)
が得られます。δ(r−r')＝δ(r'−r) なのは、r≠r'でδ＝0，r＝r'でδ＝∞ というδ関数の定義によります。その積分が、一点δ(0)の積分値1に等しいのも定義です。
(4)を、r'≠rで考えると、必ずδ＝0なので、
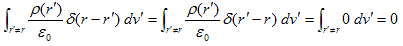(6)
です。よって(4)は、rを中心とするような十分小さな球ε上で行えば、それで十分です。ε→0（r'→r）の極限を考えます。すると(5)より、
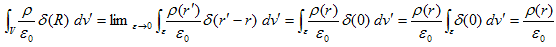(7)
となり、
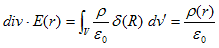
すなわちCoulombの法則、
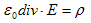(8)
が再び得られます。2.(3)は、実験で確認できる点電荷のCoulombの法則から、このようにして得られました。そこで使用された数学は、多少違ったかも知れませんが。
ところで、
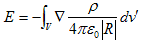
でした。そこで、rに作用するrot を用い、積分がr'に関するものである事に、再び注意すると、
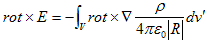
となります。
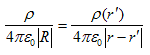
が、位置rのみで決まるポテンシャルである事は明らかです。この場合は、rot×∇＝0は、ベクトル解析の公式になるのでした。よって、
rot×E=0
が得られ、Ｅを導くようなポテンシャルφが存在します。
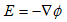
−符号を付けるのは、保存場に関する慣わしです（＝∇φでも、本当はOK）。この定義と公式div･∇＝Δにより、(8)は、
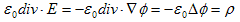
すなわち、
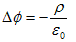
となって、静電場の法則2.(1)に戻れます。
６．まとめ
どうでしょうか？。自分の経験では、静電気に関する基本事項を、こんなにコンパクトにまとめられたのは初めてです。これはもちろん、参考にした本の手際の良さの反映ですが、ここでは 一般法則 → 実験事実 → 一般法則 という順序を取りました。今回の参考文献は、
[1] 現代物理学叢書，電磁力学，牟田泰三，2001年，岩波書店．
です。これの第１章 静電気現象を読んでみたとき、ベクトル解析の知識と、δ関数の実用的扱いさえ出来れば、静電現象の基本原理は、ほんの数ページにまとめられるような気がしてきて、この投稿に踏み切りました。
