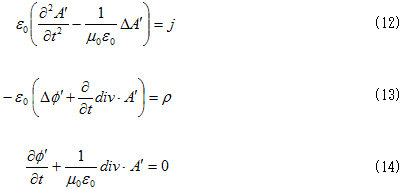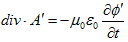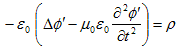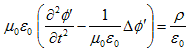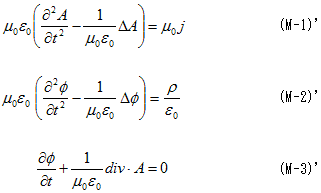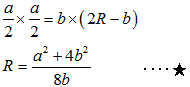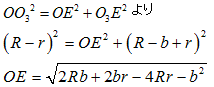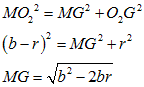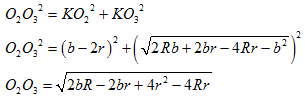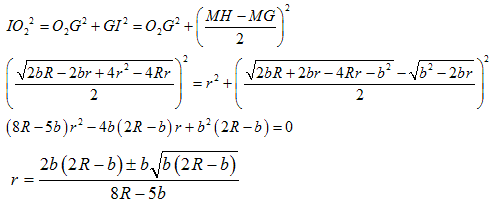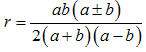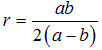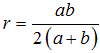NO.1855丂丂丂嶰妏宍偺俋暘妱(2)丂丂丂2010.5.29.丂丂栭傆偐偟偺偮傜偄偍偠偝傫
 乮侾乯
乮侾乯
巐妏宍俙俛俠俢偺奺曈偺拞揰傪偮側偓傑偡丅
拞揰楢寢掕棟偐傜丄
丂丂俹俽//俙俠//俻俼
丂丂俀俹俽亖俙俠亖俀俻俼
丂丂丂乮俹俽偲俻俼偑暯峴偱挿偝偑摍偟偄乯
傛偭偰丄巐妏宍俹俻俼俽偼暯峴巐曈宍偱偡丅
俙俠偲俹俻丄俽俼偺岎揰傪偦傟偧傟倃丄倄偲偡傟偽丄
柺愊偵偮偄偰丄
丂丂俀仩俹倃倄俽亖仮俢俙俠丂丒丒丒丂(嘥)
丂丂仩俹倃倄俽亖俀仮俢俹俽
傛偭偰丄
丂丂仮俙俹倃亄仮俠俽倄亖仮俢俹俽
 摨條偵丄
摨條偵丄
丂丂俀仩俻倃倄俼亖仮俛俠俙丂丒丒丒丂(嘦)
丂丂仩俻倃倄俼亖俀仮俛俻俼
傛偭偰丄
丂丂仮俙俻倃亄仮俠俼倄亖仮俛俻俼
(嘥)偲(嘦)偺曈乆傪壛偊傞偲丄
丂丂俀仩俹俻俼俽亖仩俙俛俠俢
丂丂乮偮傑傝丄暯峴巐曈宍偼傕偲偺巐妏宍偺敿暘偺柺愊乯
傑偨丄
丂丂俀乮仮俢俹俽亄仮俛俻俼乯亖俀乮仮俙俹俻亄仮俠俼俽乯亖仩俹俻俼俽
丂丂乮偮傑傝丄愒偺榓偲惵偺榓偑摍偟偔丄墿椢偺敿暘乯
乮俀乯
巐妏宍偺奺曈傪俁摍暘偡傞丅
恾偺嶰妏宍偺柺愊傪丄偦傟偧傟乮偁乯丄乮偄乯丄乮偆乯丄乮偊乯偲偡傞丅
丂丂偁亄偄亖俀偆
丂丂偆亄偊亖俀偄
曈乆偨偡偲丄
丂丂偁亄偊亖偆亄偄
丂丂乮惵偺榓偼丄拞墰偺巐妏宍偲摨偠柺愊乯
摨條偵丄師偺恾偱丄
丂丂偐亄偗亖偔亄偒
丂丂乮敄惵偺榓傕丄拞墰偺巐妏宍偲摨偠柺愊乯
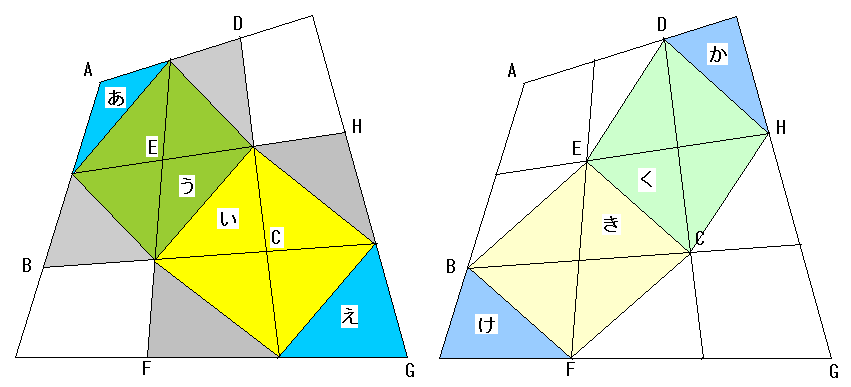
乮俁乯偙偙偱丄椢偲墿怓偺嶰妏宍偵姺嶼偟偰屄悢傪悢偊傑偡丅
丂忋偺嵍偺恾偱
| 椢 | 係屄 | 丂
|
| 敄偄奃怓偼椢偵姺嶼偟偰 | 俀屄 | 丂
|
| 墿怓 | 係屄 | 丂
|
| 擹偄奃怓偼墿怓偵姺嶼偟偰 | 俀屄 |
|
| 乮偁乯偲乮偊乯偼丄椢 | 侾屄 | 丂
|
| 丂丂丂丂丂丂丂丂丂墿怓 | 侾屄 |
|
| 忋偺嵍偺敀偺晹暘偼椢 | 俀屄 | 丂
|
| 丂丂丂丂丂丂丂丂丂墿怓 | 俀屄 |
|
| 椢丂崌寁 | 俋屄 | 丂
|
|---|
| 墿怓丂崌寁 | 俋屄 |
|
|---|
NO.1854丂丂丂揹帴婥妛Minimum-7乮Maxwell偺曽掱幃偺嵞惍棟乯丂丂丂2010.5.29.丂丂俢俢俿
丂埲屻丄NO.1744丂儀僋僩儖夝愅Minimum(1)丆
NO.1749丂儀僋僩儖夝愅Minimum(2)丆
NO.1752丂儀僋僩儖夝愅Minimum(3)丆
NO.1757丂儀僋僩儖夝愅Minimum(4)偺幃偼丄柍忦審偵巊偄傑偡丅
丂戣偼丄揹帴婥妛Minimum-7側偺偱偡偑丄榖偼NO.1772丂揹帴婥妛Minimum-4乮帴婥尰徾乯丂傑偱栠傝傑偡丅偲偄偆偺偼丄Minimum-4偱丄僗僇儔乕億僥儞僔儍儖偺攇摦曽掱幃傪棊偲偡丄偲偄偆戝僠儑儞儃傪傗偭偨偐傜偱偡丅
丂Minimum-4偼丄揹応俤丆帴懇俛丆儀僋僩儖億僥儞僔儍儖俙丆僗僇儔乕億僥儞僔儍儖冇偺崿偠偭偨Maxwell曽掱幃偐傜丄俙偲冇偺傒偺攇摦曽掱幃傪摫偔帠偑栚揑偩偭偨偺偱偡偑丄俤丆俛丆俙丆冇偺崿偠偭偨宍偲偄偆偺偼丄偠偮偼昗弨揑側Maxwell曽掱幃偺彂偒曽偱偼偁傝傑偣傫丅偦偆側偭偨棟桼偼丄Minimum-1乣6偱偼丄偳偪傜偐偲尵偆偲悢妛婑傝偺榖傪偡傞偨傔偵丄嵟弶偐傜俙偲冇傪慜柺偵弌偟偨偐傜偱偡丅
丂昗弨揑側彂偒曽偱Maxwell曽掱幃偼丄揹応俤丆帴応俫丆揹懇俢乮偙偙偱偺梡岅偱偼揹婥曄埵乯丆帴懇俛偱彂偐傟傑偡丅偦傟傪偁偘傞偲丄
丂丂
偲側傝傑偡丅倞偼揹棳枾搙丆兿偼揹壸枾搙偱偡丅俫偲俛丆俤偲俢偺娭學偼埲壓偱偡丅
丂丂
偙偙偵丄
丂兠0丗恀嬻偺桿揹棪
丂兪0丗恀嬻偺摟帴棪
丂暔棟揑偵應掕偱偒傞偺偼丄儀僋僩儖億僥儞僔儍儖俙丆僗僇儔乕億僥儞僔儍儖冇偱偼側偔丄帴応俫乮俛乯偲揹応俤乮俢乯偺曽偱偡丅廬偭偰幚尡帠幚乮偲偦偺堦斒壔乯偵拤幚偵Maxwell曽掱幃傪彂偔側傜丄(M-1)乣(M-4)偲偄偆帠偵側傝傑偡丅慜夞傑偱偼幚尡帠幚偵拤幚偱偁傞帠傪懹偭偨偨傔偵丄(M-2)偲(M-4)偺暔棟揑堄枴偯偗偑晄柧妋偱丄偦偺偨傔偵Minimum-4偵偍偄偰丄僗僇儔乕億僥儞僔儍儖偺攇摦曽掱幃傪棊偲偡丄偲偄偆戝僠儑儞儃傪偟偱偐偟傑偟偨丅
侾丏Maxwell曽掱幃偺戞1偺慻
丂傑偢(M-1)偲(M-2)傪丄Maxwell曽掱幃偺戞1偺慻偲屇傃傑偡丅(M-2)偼丄惷帴婥尰徾偵偍偄偰丄扨撈偺帴壸偼懚嵼偟側偄偲偄偆丄惷帴応偵娭偡傞Coulomb偺幚尡帠幚偺堦斒壔偱偡丅
丂惷帴応偵娭偡傞幚尡帠幚偺堦斒壔偲偄偆偺偼丄(M-1)偐傜柧傜偐側傛偆偵丄帪娫揑偵曄摦偡傞帴懇偵懳偟偰傕丄偙傟偑梫媮偝傟偰偄傞偐傜偱偡丅(M-2)偼寢嬊丄帪娫揑偵曄摦偡傞帴懇偵懳偟偰傕丄幚尡揑偵妋擣偝傟傑偡丅側偺偱Minimum-2偱傗偭偨傛偆偵丄帴懇俛傪丄儀僋僩儖億僥儞僔儍儖俙傪梡偄偰丄
丂丂 丂丂丂丂丂丂(1)
丂丂丂丂丂丂(1)
偲掕媊偡傞偺偼寢壥揑偵偼惓偟偄偺偱偡偑丄應掕偱偒傞偺偼俛乮俫乯偺傒偩偲偄偆暔棟揑忬嫷傪峫偊傞偲丄偙傟偼榑棟揑弴彉偑媡偱偡丅偲偄偆偺偼丄掕媊(1)傪庴偗擖傟傞偲悢妛揑偵偼丄帴懇俛偵偼丄
丂丂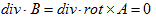
偲偄偆峉懇忦審偑晅偔偐傜偱偡丅偙傟傪丄乽(M-2)偲摨偠偩偐傜偳偆偱傕椙偄偠傖側偄偐乿偲巚偆偺偼丄埨堈偡偓傞婥偑偟傑偡乮仼 慜夞傑偱偺帺暘乯丅
丂暔棟揑側帠懺偼媡偱偡丅應掕偱偒傞偺偼俛乮俫乯偺傒偲偄偆暔棟揑帠懺偲傑偲傕偵岦偒崌偆側傜丄
丂丂丂(M-2)傪Maxwell偺曽掱幃偺拞偵柧婰偡傞偺偼摉慠丏
偲側傝傑偡丅偦偟偰丄媡偵(M-2)偑儀僋僩儖億僥儞僔儍儖摫擖偺摦婡晅偗丄偱偡丅幚尡偑(M-2)傪巟帩偡傞偐傜(1)側偺偩丄偲偄偆偺偑杮嬝偲巚偊傑偡丅
丂(1)偺傕偲偵丄(M-1)偼師偺傛偆偵曄宍偱偒傑偡丅
丂丂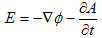 丂丂丂丂丂丂(2)
丂丂丂丂丂丂(2)
丂偙偙偵冇偼丄擟堄偺僗僇儔乕億僥儞僔儍儖偱丄rot亊佫亖0傪巊偭偰偄傑偡丅
俀丏Maxwell曽掱幃偺戞2偺慻
丂(M-3)偲(M-4)傪丄Maxwell曽掱幃偺戞2偺慻偲屇傃傑偡丅(M-4)偼丄惷揹応偵娭偡傞Coulomb偺幚尡帠幚偺堦斒壔偱偡丅
丂惷揹応偵娭偡傞幚尡帠幚偺堦斒壔偲偄偆偺偼丄(M-3)偐傜柧傜偐側傛偆偵丄帪娫揑偵曄摦偡傞揹懇偵懳偟偰傕丄偙傟偑梫媮偝傟偰偄傞偐傜偱偡丅帪娫揑偵曄摦偡傞揹懇偵懳偟偰傕幚尡揑偵妋擣偝傟偨偲偄偆揰偱偼丄(M-4)傕(M-2)偲摨偠偱偡偑丄(M-3)偺摫弌偲偄偆棟榑偺敪揥夁掱偺暥柆偵偍偄偰丄(M-4)偼(M-2)傛傝傕偢偭偲嫮偄暔棟揑梫惪偵側偭偰偄傑偟偨丅偵傕娭傢傜偢丄Minimum-4偱(M-4)傪柍帇偟偨偺偼丄寢壥揑偵傕惓偟偔側偄偱偡丅
丂(M-3)偺摫弌偺暥柆偲偼丄師偺宱堒偱偡丅摉弶Ampare偺朄懃(M-3)偼丄師偺宍偱摼傜傟偰偄傑偟偨丅
丂丂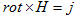 丂丂丂丂丂(1)丗Biot-Savart偺幚尡傛傝捈愙摼傜傟傞Ampare偺朄懃
丂丂丂丂丂(1)丗Biot-Savart偺幚尡傛傝捈愙摼傜傟傞Ampare偺朄懃
丂偙偙偱倞偼掕忢揹棳偱偁傝丄揹応俤乮俢乯偺帪娫揑曄壔偼偁傝傑偣傫丅椉曈偺div傪偲傞偲丄
丂丂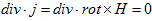
偑摼傜傟傑偡丅
丂偙傟偲揹壸偺曐懚懃丄
丂丂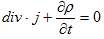 丂丂丂丂丂丂丂丂丂(2)丗揹壸偺曐懚懃
丂丂丂丂丂丂丂丂丂(2)丗揹壸偺曐懚懃
傪斾傋傞偲丄
丂丂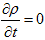 丂丂丂丂丂丂(3)
丂丂丂丂丂丂(3)
偲偄偆寢榑偑弌傑偡丅倞偑掕忢揹棳偺応崌偼惷揹応偱丄摉慠揹壸枾搙兿傕帪娫揑偵曄壔偟側偄偺偱丄(3)偼懨摉側寢榑偱偡丅偟偐偟帪娫揑偵曄摦偡傞揹応偺応崌丄佪兿/佪t亖0偲偼尷傜側偄偺偱丄Ampare偺朄懃偺尨宍(1)偼丄帪娫揑偵曄摦偡傞揹応偵偍偄偰丄揹壸偺曐懚懃(2)傪攋傞帠偵側傝傑偡丅(2)偲惍崌偡傞傛偆偵(1)傪奼挘偟偨偺偑丄Maxwell偱偡丅
丂壗屘(2)傪庣傞曽岦側偺偐偲尵偊偽丄儀僋僩儖夝愅-1偱傗偭偨傛偆偵丄(2)偼棳検曐懚懃側偺偱棳懱椡妛偵偍偄偰傕摨條側幃偑摼傜傟丄暔棟揑忬嫷偵娭傢傜偢惉傝棫偮丄堦庬偺悢妛揑峆摍幃偲傒側偣傑偡丅Minimum-4偱傕摨偠庯巪偺帠傪尵偄傑偟偨偑丄偙傟偼惓偟偐偭偨偲巚偄傑偡丅
丂(2)傪庣傞傛偆偵(1)傪奼挘偡傞偲偡傟偽丄師偺傛偆側娭學偵側傝傑偡丅div丒rot亊亖0偼峆摍幃側偺偱丄
丂丂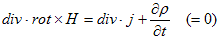
偑昁梫偱偡丅佪兿/佪t傪嵍曈傊堏崁偟丄
丂丂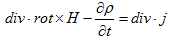 丂丂丂丂丂丂(4)
丂丂丂丂丂丂(4)
偲側傝傑偡偑丄偙偙偱(M-4)偑搊応偟傑偡丅(M-4)偼摉弶惷揹応偐傜摼傜傟偨幚尡帠幚偱偟偨偑丄偙傟偑帪娫曄摦偡傞揹応偱傕惉傝棫偮偲梫惪偟傑偡丅(M-4)傪(4)偵戙擖偡傟偽丄
丂丂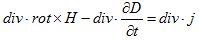
偲側傝丄
丂丂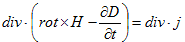
偐傜丄
丂丂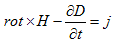 丂丂丂丂丂(M-3)
丂丂丂丂丂(M-3)
偑昁梫偱偁傞帠傪摫偗傑偡丅偙偺宱堒偐傜偟偰丄(M-4)傪棊偲偡帠偼弌棃側偐偭偨偼偢側偺偱偡偑丄Minimum-4偱偼丄儀僋僩儖億僥儞僔儍儖俙偱彂偐傟偨(M-1)偲(M-3)偲偐傜(M-4)傪摫偗傞偲偟偰丄Maxwell曽掱幃偐傜(M-4)傪彍奜偟傑偟偨乮(M-2)偵偮偄偰偼丄嵟弶偐傜彍奜偝傟偰偄偨乯丅暔棟揑堄枴偐傜偡傞偲丄憗崌揰傕偄偄偲偙傠偱偡丅
丂埲壓偦偺憗崌揰偱偡丅
丂惷揹応偼揹応扨撈偺尰徾側偺偱丄1.(2)偱俙亖0偲偱偒傑偡丅
丂丂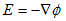 丂丂丂丂丂丂(5)
丂丂丂丂丂丂(5)
偲側傝丄僗僇儔乕億僥儞僔儍儖偱彂偐傟偨惷揹応偺掕媊偑弌偰偒傑偡丅傑偨Ampare偺朄懃(M-3)丆揹壸曐懚懃(2)偲1.(2)傪慻傒崌傢偣傞偲丄
丂丂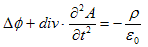 丂丂丂丂丂丂(6)
丂丂丂丂丂丂(6)
偲側偭偰丄偙偙偱傕俙亖0偲偡傟偽丄
丂丂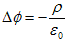 丂丂丂丂丂丂(7)
丂丂丂丂丂丂(7)
偲側傝丄惷揹応偺僗僇儔乕億僥儞僔儍儖偱彂偐傟偨Coulomb偺朄懃偑摼傜傟傑偡丅
丂(5)偲(7)偵丄揹懇偺掕媊(M-6)傪巊偆偲丄師偺(8)偑弌傑偡丅
丂丂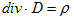 丂丂丂丂丂丂(8)
丂丂丂丂丂丂(8)
丂(8)偼(M-4)偲摨偠宍傪偟偰偄傑偡偑丄偁偔傑偱惷揹応偺応崌偱偡丅帪娫曄摦偡傞揹応偱傕(8)偱偁傞偲丄曐徹偡傞傕偺偱偼偁傝傑偣傫丅偵傕娭傢傜偢丄(M-4)傪Maxwell偺曽掱幃宯偐傜彍奜偟傑偟偨丅
丂偙偺堄幆偺掅偝偼丄寢嬊(M-2)傪彍奜偟偨偺偲摨偠偱丄榑棟揑弴彉偑媡偱偡丅應掕偱偒傞偺偼俤乮俢乯偺傒偲偄偆暔棟揑帠懺偲傑偲傕偵岦偒崌偆側傜丄
丂丂丂(M-4)傪Maxwell偺曽掱幃偺拞偵柧婰偡傞偺偼摉慠丏
偲偼丄尵偆傑偱傕側偄帠偵側傝傑偡丅儅僗僞乕傕偟偰偄側偄偺偵俙偲冇偐傜弌敪偡傞偺偼丄傗偼傝丄傗傝曽偲偟偰娫堘偭偨曽岦偩偭偨偲巚偄傑偡乮僾儘偼傗偭偰傕戝忎晇偱偟傚偆偑乯丅暔棟偱偼悢妛埲忋偵丄尰幚偲偺懳墳偑尩偟偄丄偲偄偆摉慠偺寢壥偱偟偨丒丒丒丅
丂偱偼(5)丆(7)丆(8)偼柍堄枴偩偭偨偺偱偟傚偆偐丠丅偄偪偍偆柍堄枴偱偼側偐偭偨丄偲巚偭偰偄傑偡丅偲偄偆偺偼丄惷揹応偺Coulomb偺朄懃丆Faraday偺朄懃丆Ampare偺朄懃偼撈棫偵摼傜傟偨寢壥偱丄屻偺2偮偑嵟弶偺偲惍崌偡傞偐偼丄傗偭偰傒傞傑偱傢偐傝傑偣傫丅傕偪傠傫傗偭偰傕柕弬偟側偄偐傜丄偙傫側帠偼偳傫側杮偵傕嵹偭偰側偄傢偗偱偡偑丄柕弬偟側偄帠偑妋擣偝傟偨帪揰偱丄惷揹応偺Coulomb偺朄懃偼幪偰傞帠偑偱偒偨偺偩偲巚偊傑偡丅偨偩偟丄帪娫曄摦偡傞揹応偺Coulomb偺朄懃傑偱幪偰傜傟傞傢偗偱偼偁傝傑偣傫乮仼 偙偙偱娫堘偭偨両乯丅
丂偟偐偟媡偺帠懺傕偁傝摼偨傢偗偱偡丅椺偊偽丄1.(2)偲(6)丄
丂丂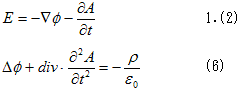
偐傜(8)偑摫偐傟偰偟傑偭偨傜丄帪娫曄摦偡傞揹応偺Coulomb偺朄懃傕幪偰偰椙偄帠偵側傝傑偡丅傕偪傠傫幪偰傜傟側偄偐傜丄媡偵偳傫側杮偵傕(M-4)偼嵹偭偰傞偺偱偡偑丄棟桼偑昁梫偱偡丅偲偄偆偺偼暔棟偱偼丄堦晹偺幃傪挱傔偨偩偗偱偼丄偦傟偑杮摉偵朄懃偵昁梫偐偳偆偐偺寛掕懪偵側傜側偄偐傜偱偡丅椺偊偽丄1.(2)偲(6)偐傜(8)傪摫偔傛偆側丄悢妛揑壖掕傪捛壛偡傞帠偼娙扨偵弌棃傑偡丅偦偟偰偦偺悢妛揑壖掕偑惓偟偄偐偼丄幚尡傪帩偮側偳偲偄偆帠傪傗偭偰偄偨傜丄栘傪尒偰怷傪尒側偄帠懺偵側傝傑偡丅偮傑傝丄朄懃偑暵偠偰偄傞偐偳偆偐傪敾掕偡傞昁梫偑偁傝傑偡丅偙偺榖傕Minimum-4偱偼棊偪偰偄傑偟偨偑丄偙偙偼悢妛偺弌斣偱偡丅
俁丏Maxwell曽掱幃偼暵偠偰偄傞
丂Maxwell曽掱幃偺宯傪嵞婰偟傑偡丅
丂丂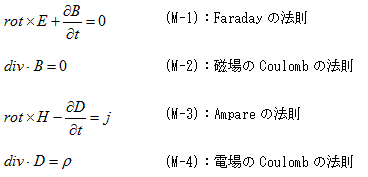
丂榖偺尒捠偟傪椙偔偡傞偨傔偵丄(M-1)偲(M-3)偺div傪庢傝傑偡丅div丒rot亊亖0偵拲堄偡傞偲丄(M-2)偐傜偼丄
丂丂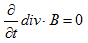 丂丂丂丂丂丂(1)
丂丂丂丂丂丂(1)
偲側傝傑偡丅偨偩偟div丒偲佪/佪t偑岎姺偱偒傞帠傪巊偄傑偟偨丅摨條偵(M-3)偐傜丄
丂丂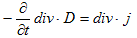
偑摼傜傟丄揹壸偺曐懚懃2.(2)傛傝div丒j傪丄佪兿/佪t偵偍偒偐偊傞偲丄
丂丂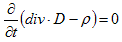 丂丂丂丂丂丂(2)
丂丂丂丂丂丂(2)
傪摼傑偡丅
丂師偵丄朄懃偑暵偠偰偄傞偲偼丄朄懃傪昞傢偡曽掱幃宯偐傜丄朄懃傪昞傢偡暔棟検傪慡偰寛掕偱偒傞丄偲偄偆堄枴偱偡丅椺偊偽屆揟椡妛偺Newton偺塣摦曽掱幃側傜丄倣傪幙検丆r傪棻巕偺曄埵儀僋僩儖丆俥傪曐懚椡偲偟偰丄
丂丂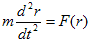 丂丂丂丂丂丂(3)
丂丂丂丂丂丂(3)
偱偡丅暔棟検偼3師尦儀僋僩儖r偱丄3屄偺帪娫偺枹抦娭悢傪寛掕偡傞昁梫偑偁傝傑偡偑丄(3)偼3師尦偺儀僋僩儖曽掱幃偱丄3屄偺2奒忢旝暘曽掱幃傪昞傢偡偺偱丄弶婜忦審傪彍偒丄3屄偺枹抦娭悢傪姰慡偵寛掕偡傞偺偑傢偐傝傑偡丅偙偙偱弶婜忦審偺晄掕惈偼杮幙揑偱偼偁傝傑偣傫丅
丂椺偊偽曻暔塣摦傪峫偊偨帪丄憐掕偟偨弶婜帪崗偵偍偗傞弶婜忦審傪巊偭偰傕丄曻暔慄偺搑拞偺帪揰偵偍偗傞(埵抲丆懍搙)傪弶婜忦審偲偟偰傕丄寢嬊摨偠曻暔慄偑摼傜傟傑偡丅偙偺傛偆偵寢壥傪曄偊偢偵丄恖娫偺湏堄惈偵傛偭偰偳偆偲偱傕側傞忦審偼丄朄懃偑暵偠傞乛暵偠側偄偲柍娭學偲峫偊傜傟傑偡丅寢壥偱偁傞曄埵儀僋僩儖r偑曄傢傜側偄偐傜偱偡丅
丂(M-1)乣(M-4)偵偍偄偰暔棟検偼丄揹応俤偲帴応俫偱偡丅揹懇俢偲帴懇俛偼丄1.偺(M-5)丆(M-6)傛傝俤偲俫偵斾椺偟傑偡丅俤偲俫偼3師尦偺儀僋僩儖偱丄6屄偺枹抦娭悢傪寛掕偡傞昁梫偑偁傝傑偡丅堦曽丄(M-1)乣(M-4)偼丄惓枴8屄偺曃旝暘曽掱幃偵側偭偰偄傑偡丅
丂枹抦悢偺悢傛傝忦審悢偑懡偄帪丄峫偊傜傟傞帠懺偼丄師偺3偮偱偡丅
丂丂丂a) Maxwell曽掱幃偼丄柕弬偟偰偄傞丏
丂丂丂b) 8屄偺偆偪2屄偼丄懠偺忦審偐傜摫偗傞丏
丂丂丂c) 2屄偼丄弶婜忦審偺椶傪昞傢偟偰偄傞丏
丂傕偪傠傫Maxwell曽掱幃偑暵偠偰偄傞偲偡傞側傜丄偺榖偱偡丅偦偆偱側偄偲偡傞側傜丄傕偭偲慖戰巿偼憹偊傑偡乮楢棫1師曽掱幃偑丄惓懃偐偳偆偐偺榖偲摨偠偱偡乯丅
丂(M-1)偲(M-3)偵拲栚偟傑偡丅偙傟傜偼6屄偺曃旝暘曽掱幃傪峔惉偟丄帪娫偺曃旝暘偑偁傝傑偡丅偲偄偆帠偼丄偙傟傜偱揹応俤偲帴応俫偺帪娫敪揥偼丄姰慡偵寛傑傞偼偢偱偡丅偳偺傛偆偵寛傑傞偐傪尒傞偨傔偵丄(M-1)偲(M-3)傪師偺傛偆偵曄宍偟丄僨僕僞儖偵乮嵎暘偱乯峫偊傑偡丅
丂丂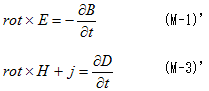
丂(M-1)乫偲(M-3)乫偱丄偁傞帪崗偺揹応俤丆帴応俫丆揹棳枾搙倞偺嬻娫暘晍偑寛傑傟偽乮嵍曈乯丄偦傟偑帴懇俛偲揹懇俢偺帪娫曄摦傪寛傔傑偡乮塃曈乯丅俫偲俤偼丄俛丆俢偵斾椺偟傑偡丅偦偆偡傞偲廫暘抁偄帪娫屻偺俤偲俫偺嬻娫暘晍偑寛傑傝傑偡丅倞偵偮偄偰偼師偺傛偆偵側傝傑偡丅
丂倞偺幚懱偼懍搙傪帩偭偨壸揹棻巕e偱偡丅e偵丄俤偲俫偱寛傑傞Loreants椡傪揔梡偟丄塣摦曽掱幃傪棫偰傞帠偵傛傝丄佪倞/佪t傕寁嶼偱偒傞帠偵側傝傑偡丅慜夞傑偱偼柍帇偟偰棃傑偟偨偑丄壸揹棻巕傪娷傓揹帴応偺宯偱偼丄杮摉偼Newton偺塣摦曽掱幃傕昁梫偱偡丅
丂偄偢傟偵偟傠嵍曈偺嬻娫暘晍偑丄奺暔棟検偺塃曈偺帪娫曄摦傪寛掕偟丄堦弖屻偺暔棟検偺嬻娫暘晍傪寛傔傑偡丅偡傞偲(M-1)乫丆(M-3)乫乮偲塣摦曽掱幃乯偵廬偭偰丄傕偆堦弖屻偺嬻娫暘晍傕寛傑傝丒丒丒偲丄帪娫敪揥偼姰慡偵婰弎偱偒傑偡丅(M-1)偲(M-3)偼暵偠偰偄傑偡乮梋寁側傕偺偼側偄偟丄懌傝側偄傕偺傕側偄)丅
丂偟偐偟曃偱偁傠偆偲忢偱偁傠偆偲丄旝暘曽掱幃偱寛掕偝傟傞帪娫敪揥偺晄掕惈傪徚偡偵偼丄弶婜忦審偑昁梫偱偡乮愭偺塣摦曽掱幃偲摨偠乯丅(M-1)乫偲(M-3)乫偱峫偊傟偽丄寁嶼傪僗僞乕僩偝偣傞偨傔偵丄弶婜帪崗偵偍偗傞俤偲俫乮偲倞乯偺嬻娫暘晍傪梌偊傞昁梫偑偁傝傑偡丅偙偺帪丄(M-2)偲(M-4)偑昁梫側暔棟揑梫惪偱偁傞側傜偽乮幚尡帠幚偐傜偦偆尒偊傞乯丄弶婜暘晍偼丄峉懇忦審(M-2)丆(M-4)傪枮偨偡昁梫偑偁傝傑偡丅
丂偦偺傛偆偵偟偰弶婜暘晍傪梌偊偨偲偟偰丄屻偼(M-1)偲(M-3)偑丄懠偺忦審偄偭偝偄晄梫偱丄帪娫敪揥傪寛傔傑偡丅偙偺寢壥偑丄(M-2)丆(M-4)偲惍崌偡傞偺傪曐徹偡傞偺偑丄嵟弶偵摫偄偨(1)偲(2)偱偡丅偮傑傝丄弶婜帪崗偱(M-2)偲(M-4)偑惉傝棫偰偽丄偦傟埲屻丄偢偭偲惉傝棫偭偰偄傑偡丅(1)偲(2)偼丄Faraday偺朄懃偲Anpare偺朄懃偵娷傑傟傞寢壥偱偟偨丅揹帴応曽掱幃偭偰丄偆傑偔弌棃偰傑偡傛偹丠丅
丂(M-2)丆(M-4)偼丄c)弶婜忦審偺堦晹偩偭偨丄偲偄偆偺偑寢榑偱偡丅Newton偺塣摦曽掱幃偱尵偊偽丄
丂丂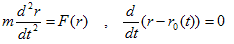
偲偄偆彂偒曽偱偡丅偙偙偱r0(t)偼丄弶婜埵抲傪0偲偟偨夝偱偡丅傕偆彮偟嬤偯偗傞偲丄
丂丂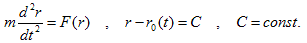
偲偄偆帠偱偁傝丄塣摦曽掱幃偑旝暘曽掱幃偱偁傞帠偐傜捈愙弌偰偔傞丄塣摦曽掱幃偵娷傑傟傞寢壥偱偡丅塣摦曽掱幃偺応崌偼丄嵟屻偺宍傕悢妛揑偵帺柧丄偮傑傝幚尡帠幚晄梫偲偼彮偟尵偄夁偓偱偡偑丄偄偪偍偆彂偔昁梫側偟偲側傝傑偡丅
丂Maxwell曽掱幃偺応崌偼丄擟堄偺帪崗傪弶婜帪崗偲偟偰椙偄帠丄懄偪丄偄偮偱傕偳偙偱傕(M-2)偲(M-4)偲偄偆暔棟揑梫惪偑惉傝棫偭偰偄傞偺偱丄偦傟傜傪徣棯偡傞帠偼偱偒傑偣傫丅
4丏Lorents僎乕僕
丂嵟屻偵Lorents僎乕僕偵堏傝丄揹帴億僥儞僔儍儖俙偲冇偺攇摦曽掱幃傪摫偒傑偡丅Minimum-4偱堦搙偼敿暘傗偭偨帠側偺偱丄庤抁偵峴偒傑偡丅
丂Maxwell曽掱幃偺宯傪嵞婰偟傑偡丅
丂丂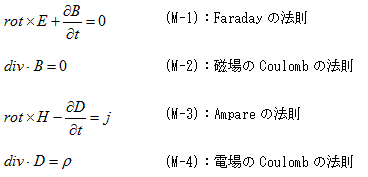
丂偙偙偵丄
丂丂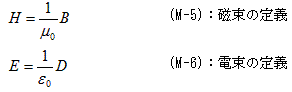
丂兠0丗恀嬻偺桿揹棪
丂兪0丗恀嬻偺摟帴棪
丂Maxwell曽掱幃偺戞1偺慻(M-1)丆(M-2)偱丄(M-2)偑儀僋僩儖億僥儞僔儍儖俙偺摫擖傪摦婡晅偗丄
丂丂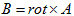 丂丂丂丂丂丂(1)
丂丂丂丂丂丂(1)
偲弌棃傑偡丅(1)傪(M-1)偵戙擖偡傞偲丄
丂丂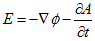 丂丂丂丂丂丂(2)
丂丂丂丂丂丂(2)
傪摼傑偡丅偙偙傑偱偱丄俙偲冇偼擟堄偱偡丅俙偲冇偺寛掕曽掱幃偼丄Maxwell曽掱幃偺戞2偺慻(M-3)丆(M-4)偱偡丅(1)丆(2)傪(M-3)偵戙擖偡傞偲丄師偺(3)傪摼傑偡丅
丂丂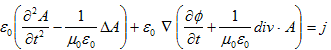 丂丂丂丂丂丂(3)
丂丂丂丂丂丂(3)
丂(2)傪(M-4)偵戙擖偟傑偡丅div丒佫亖儮傪巊偄丄嵍曈丗
丂丂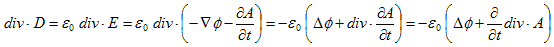
偲側傞偺偱丄
丂丂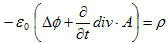 丂丂丂丂丂丂(4)
丂丂丂丂丂丂(4)
偑摼傜傟傑偡丅偙偙偱Lorents僎乕僕偵堏傝傑偡丅
丂Minimum-4偱偼(3)偟偐側偐偭偨偺偱丄冇偼慡偔偺擟堄偱丄扨弮偵(3)偺戞2崁傪0偵偡傞傛偆側冇傪慖傃傑偟偨偑丄崱偼(4)偑偁傞偺偱丄偦偆偼峴偒傑偣傫丅傕偆堦岺晇昁梫偱偡偑丄敪憐偼摨偠偱偡丅
丂rot亊佫亖0偵拲堄偡傞偲丄(1)偵偼丄
丂丂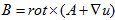
偺晄掕惈偑偁傝傑偡乮晄掕惈偑偁傞偑屘偵丄億僥儞僔儍儖偱偡乯丅偙偙偱u偼擟堄偺僗僇儔乕娭悢偱偡丅傑偨(2)偼傕偲傕偲丄
丂丂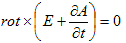 丂丂丂丂丂丂(5)
丂丂丂丂丂丂(5)
偺rot亊偵懳偡傞愊暘掕悢乮傒偨偄側傕偺乯偲偟偰丄冇傪摫擖偟偰偄偨偺偱丄
丂丂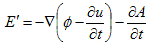
偲偄偆宍傕嫋偝傟傑偡乮(5)偺傒偐傜偼乯丅偝傜偵忋幃偺塃曈偱丄俙偑俙亄佫u偱偁偭偨偲偡傞偲丄
丂丂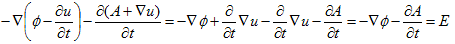
偲側傝丄嵟弶偺俤偵栠傟傑偡丅偮傑傝俙偲冇偵偼丄彮側偔偲傕擟堄偺僗僇儔乕娭悢u堦屄暘偺晄掕惈偑偁傝傑偡丅偦偙偱丄
丂丂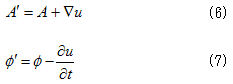
偲偍偄偰丄(6)丆(7)傪(3)偺嵍曈偺奺崁偵戙擖偡傞偲丄
丂丂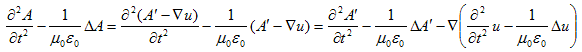
丂丂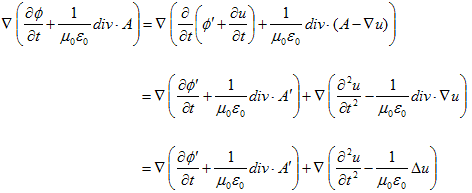
偲側傝傑偡丅偨偩偟丄div丒佫亖儮傪巊偭偰偄傑偡丅偙傟傜偺寢壥傪丄(3)偺嵍曈偵戙擖偡傞偲丄奺幃偺2崁栚偼徚偟偁偄丄
丂丂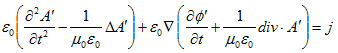 丂丂丂丂丂丂(8)
丂丂丂丂丂丂(8)
摼傜傟丄曄姺(6)丆(7)偺傕偲偱(3)偼晄曄側偺偑傢偐傝傑偡丅(4)傕晄曄偵側傝丄僎乕僕曄姺(6)丆(7)偺傕偲偱丄Maxwell曽掱幃偼晄曄偲尵偆偦偆偱偡丅媡偵丄Maxwell曽掱幃傪晄曄偵偡傞(6)丆(7)傪媮傔傞帠偑僎乕僕棟榑偺弶曕偱偡偑丄偙偙偱偼偙傟埲忋傗傝傑偣傫丅
丂丂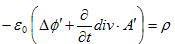 丂丂丂丂丂丂(9)
丂丂丂丂丂丂(9)
丂(8)偺戞2崁偑0偵側傞傛偆偵丄u傪掕傔傑偡丅旝暘墘嶼巕偺慄宍惈偲丄俙偲冇偑傕偲傕偲(3)傪枮偨偡偲偄偆帠偐傜丄(8)偺2崁栚傪0偲偍偄偰丄俙乫偲冇乫傪丄俙偲冇偲u偲偱彂偄偰傗傟偽丄
丂丂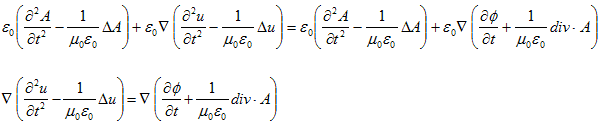
偲側傝傑偡偑丄u偵娭偡傞忦審偼丄昁梫嵟彫尷偱椙偄偺偱丄
丂丂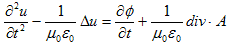 丂丂丂丂丂丂(10)
丂丂丂丂丂丂(10)
偱偁傟偽廫暘偱偡丅(10)偑u偵娭偡傞曗彆曽掱幃偱偡丅(10)偼旕惸師偺攇摦曽掱幃側偺偱丄俙偲冇偑懚嵼偡傞側傜丄u偺懚嵼偼曐徹偝傟傑偡丅俙偲冇偼丄(3)丆(4)偐傜寛掕偝傟傑偡偑丄(3)丆(4)偼Maxwell曽掱幃(M-1)乣(M-4)偺尵偄姺偊側偺偱丄懚嵼偡傞偲峫偊傑偡丅屘偵u偼懚嵼偟傑偡丅
丂u偵偮偄偰偼丄偦偺懚嵼偝偊妋擣偱偒傟偽丄OK偱偡丅(10)傪夝偔昁梫偼偁傝傑偣傫丅(10)偼丄僎乕僕曄姺(6)丆(7)偺傕偲偵丄(8)偵偍偄偰丄
丂丂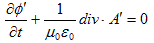 丂丂丂丂丂丂(11)
丂丂丂丂丂丂(11)
偲偍偔帠偵傛偭偰摼傜傟傞傕偺偱偡丅僎乕僕曄姺(6)丆(7)偺傕偲偱Maxwell曽掱幃(3)丆(4)偼晄曄偱丄(8)丆(9)偑摼傜傟丄偟偐傕暔棟検俤偲俫傕晄曄偱偡丅
丂廬偭偰丄(8)丆(9)傪嵟弶偐傜婎杮朄懃偲偟偰椙偔乮僎乕僕晄曄惈乯丄
俙偲冇傪摿偵寁嶼偟傗偡偄宍偵偡傞偨傔偵丄俙偲冇偺晄掕惈傪(11)傪枮偨偡傛偆偵慖傫偩偩偗丄
偲尵偊傞偐傜偱偡丅
丂幚嵺(11)傪慖傇偲丄師偺曽掱幃宯傪庢傟偽椙偔側傝傑偡丅
丂丂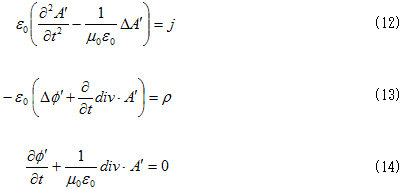
丂(12)偼丄(8)偱戞2崁傪0偲偍偄偨傕偺偱丄偦偺忦審偼(14)乮(11)偲摨偠)丄(13)偼(9)偺傑傑偱偡丅(13)偼偝傜偵娙扨偵弌棃傑偡丅(14)傛傝丄
丂丂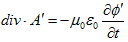
偲側傝丄忋幃傪(13)嵍曈偵戙擖偡傟偽丄
丂丂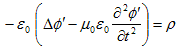
側偺偱丄
丂丂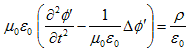
偱偡丅埲忋傑偲傔傟偽丄俙乫偲冇乫偼嵟弶偐傜杮摉偺揹帴億僥儞僔儍儖偲傒側偟偰椙偄偺偱丄俙丆冇偲彂偒丄
丂丂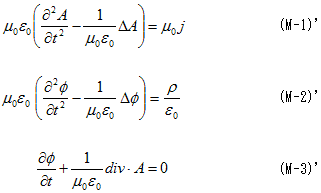
偑丄儀僋僩儖億僥儞僔儍儖俙偲丄僗僇儔乕億僥儞僔儍儖冇偱昞傢偝傟偨Mawell偺曽掱幃偱偡丅(M-3)乫傪Lorents偺僎乕僕忦審偲尵偄傑偡丅(M-1)乫偲(M-2)乫偼丄俙偲冇偵娭偟偰曄悢暘棧偝傟偰偄傑偡丅曋棙偱偡両丅偝傜偵(M-2)乫偼丄Minimum-4偱彍奜偟偨幃(4)偐傜弌偰偔傞傕偺偱偡丅
丂(M-3)乫偼棊偲偣傑偣傫丅俙偲冇偵偼愭偵弎傋偨晄掕惈偑偁傞偺偱丄(M-1)乫傑偨偼(M-2)乫傪枮偨偡擟堄偺夝偑丄(M-3)乫傪枮偨偡偲偼尷傜側偄偐傜偱偡丅廬偭偰丄(M-1)乫偲(M-2)乫傪撈棫偵夝偄偨屻丄(M-3)乫偺忦審傪枮懌偡傞丄夝俙偲冇偺慻傒崌傢偣傪慖戰偡傞昁梫偑惗偠傑偡丅
丂偱丄Minimum-5偺昡壙偼偳偆偐偲尵偆偲丄偦偙偱峴偭偨嶌梡慺偺暘夝偵偮偄偰偼丄偄偪偍偆偦偆側偺偐側丠丄偲偼巚偄傑偡偑丄寢榑偵偮偄偰偼榖敿暘偱暦偄偰壓偝偄丄偲偄偆帠偵側傝傑偡丅幚嵺偦偙偱偼丄(M-1)乫傪枮偨偡俙傪媮傔偰(M-3)乫傪巊偄丄冇傪媮傔傑偟偨丅傑偝偵丄忦審偺敿暘偟偐巊偭偰偄傑偣傫丒丒丒丅
丂偲偙傠偱丄(M-1)乫偺塃曈偱摟帴棪兪0偑暘巕偵偁傝丄(M-2)乫偺塃曈偱桿揹棪兠0偑暘曣偵棃傞偺偼偳偆偟偰側偺偩傠偆丠丄偲偄偆偺偑偪傚偭偲婥偵側傝傑偡丅(M-1)乫乣 (M-3)乫偼杮偱妋偐傔偨傕偺側偺偱丄岆怉偱偼側偄偼偢偱偡丅掕媊偺栤戣側偺偐丠丄偦傟偲傕帴婥尰徾偑揹婥尰徾偐傜摫偐傟傞偨傔側偺偐丠丄偲偐巚偄傑偡丅
俇丏傑偲傔
丂偠偮偼偙偺帺廗僲乕僩婇夋偼丄師偺杮傪撉傒偨偔偰巒傔傑偟偨丅
丂丂丂応偺屆揟榑丆儔儞僟僂丒儕僼僔僢僣丆搶嫗恾彂姅幃夛幮丆1978擭丏
丂応偺屆揟榑偼丄慡晹偱14復偁傝丄嵟弶偺2復偑摿庩憡懳惈棟榑丄3乣9復傑偱偑揹帴婥妛丄巆傝5復偑堦斒憡懳惈棟榑偲偄偆峔惉偵側偭偰偄傑偡丅
丂尰忬偼偲尵偆偲丄1復偲2復偼偦傟側傝偵撉傒傑偟偨偑丄戞3復偺朻摢傪彍偄偰偼丄埲屻偐側傝懯栚偱偡丅丂戞3復偺朻摢捈屻偵丄偄偒側傝壸揹棻巕傪娷傓揹帴応偺Lagragian偑弌偰偒傑偡丅偙偺曈傝偱傕偆丄崀嶲偱偟偨丅
丂応偺屆揟榑偼儔儞僟僂丒儕僼僔僢僣偺僔儕乕僘偺拞偱傕丄棟榑峔惉偑弌怓偺弌棃偲尵傢傟丄慡晹傪撉傒捠偝側偄偲堄枴偺側偄杮偱偡丅偟偐偟儔儞僟僂偼丄偦偺峴娫傪撉傑偹偽側傜偸帠偵娭偟偰傕丄桳柤側杮偱偡丅
丂偙偺傛偆側帠懺側偺偱丄応偺屆揟榑偺敿暘偔傜偄傪愯傔傞丄揹帴婥妛偺峴娫傪撉傔傞傛偆偵側傞偺偵偼丄傕偭偲昗弨揑側杮傪撉傓傋偒偩偲巚偄傑偟偨丅偱傕丄庤偵庢傞傛偆偵傢偐傜側偔偰傕丄応偺屆揟榑偼柺敀偄偱偡丅棟榑峔惉偑弌怓偩偐傜偱偡丅偦傟偱丄
丂丂丂尰戙暔棟妛憄彂丆揹帴椡妛丆柎揷懽嶰丆2001擭丆娾攇彂揦丏
傪丄偮傫撉忬懺偐傜堷偭傁傝弌偟傑偟偨丅旕忢偵庤嵺偺椙偄杮偩偲巚偄傑偟偨丅偦偺寢壥偑丄Mimimum-1乣6偱偡丅Mimimum-1乣6偺庤嵺偺埆偝偼丄帺暘偺愑擟偱偡丅
丂偟偐偟擺摼偱偒側偄晹暘傕偁傝傑偟偨丅慜夞傑偱偱偼堦搙傕弌偟偰偄傑偣傫偑丄僐儞僨儞僒乕偺桿揹梕検偲偐丄揹帴僄僱儖僊乕側偳偵娭偡傞晹暘偱偡丅偦傟傜傪擺摼偟偨偄偑偨傔偵丄師偺1嶜傪攦偄傑偟偨丅
丂丂丂揹帴婥妛傪峫偊傞丆崱堜岟丆僒僀僄儞僗幮丆1990擭丏
丂崱堜岟偲尵偊偽丄棳懱椡妛偺戝壠偱丄愄偼摍妏幨憸側偳偺榖偱丄怓乆偲偍悽榖偵側偭偨偍傏偊偑偁傝傑偡丅尰嵼乮1990擭乯偼丄揹帴棳懱椡妛偑愱栧偲偺帠偱偡丅
丂乽揹帴婥妛傪峫偊傞乿偼丄弌怓偺弌棃偱偡丅偟偐偟偙傟偼丄昗弨揑揹帴婥妛傪儅僗僞乕偟偨恖偺撉傓傋偒杮偲巚偊傑偟偨丅偲偄偆傢偗偱乽揹帴婥妛傪峫偊傞乿傕懯栚偱丄師偵丄掕昡偁傞嵒愳廳怣偺棟榑揹帴婥妛傪攦偄傑偟偨丅旕忢偵僆乕僜僪僢僋僗偱挌擩側杮偱偟偨丅
丂丂丂棟榑揹帴婥妛丆嵒愳廳怣丆婭埳崙壆彂揦丆1999擭丏
丂攦偭偨寢壥偑丄偙偺搳峞偱偡丅傕偟偐偡傞偲傕偆偡偖丄揹帴応偵偍偗傞僄僱儖僊乕曐懚懃丗億僀儞僥傿儞僌儀僋僩儖偲丄塣摦検曐懚懃丗Maxwell墳椡丄偵偮偄偰搳峞偡傞偐傕抦傟傑偣傫丅壗偲偐偍婅偄偟傑偡丒丒丒丒丅
NO.1852丂丂丂嶼妟偺栤戣侾(2) 丂2010.5.10.丂丂栭傆偐偟偺偮傜偄偍偠偝傫
墌俷偺敿宎傪俼丄墌俷1丄俷2丄俷3偺敿宎傪倰偲偡傞丅
尫俙俢亖倎丄俵俶亖倐側偺偱丄俵俙亖俵俢亖倎乛俀丄俵俰亖俀俼亅倐
曽傋偒偺掕棟傛傝丄
俵俙亊俵俢亖俵俶亊俵俰
丂丂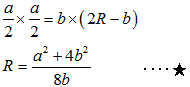
俷俤//俙俢偱偁傝丄仮俷俷3俤偑捈妏嶰妏宍側偺偱丄
丂丂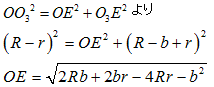
俵偐傜墌俷2傊偺愙慄偺愙揰傪俧偲偡傟偽丄仮俵俷2俧偼捈妏嶰妏宍側偺偱丄
丂丂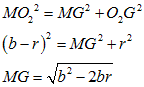
揰俷3偐傜俵俶偺悅慄俷3俲傪壓傠偡偲丄仮俲俷2俷3偼捈妏嶰妏宍側偺偱丄
乮俲俷3亖俷俤乯
丂丂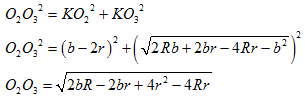
俵偐傜墌俷3傊偺愙慄偺愙揰傪俥丄俫偲偡傟偽丄俷俤亖俵俥亖俵俫
慄暘俷2俷3偺拞揰傪俬偲偡傟偽丄仮俬俷2俧偼捈妏嶰妏宍側偺偱丄
丂丂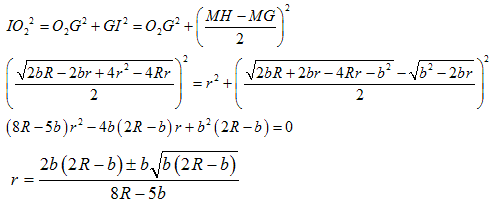
偙傟偵忋偺仛傪戙擖偡傞偲丄
丂丂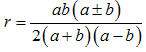
暘巕偺倎偲倐偺娫偺晞崋偑亄偺偲偒丄
丂丂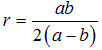
暘巕偺倎偲倐偺娫偺晞崋偑亅偺偲偒丄
丂丂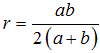
偲側傞偑丄椺偊偽倎亖俀俼丄倐亖俼傪戙擖偟偰傒傞偲丄
乽亄乿偺応崌偼倰亖俼丄乽亅乿偺応崌偼倰亖俼乛俁偲側傞偺偱丄
丂丂
偺曽偑揔摉偲峫偊傜傟傞丅
丂丂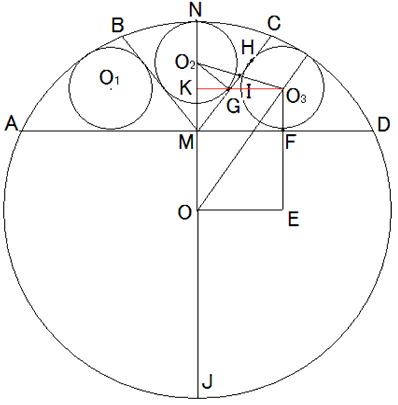
NO.1851丂丂丂嶰妏宍偺俋暘妱丂丂丂丂2010.5.4.丂丂僗儌乕僋儅儞
傕偆堦偮夝偗側偄栤戣偑偁傝傑偡...^^;
乽堦斒揑側晄摍曈巐妏宍偑侾偮偁傞偲偟傑偡丅偦偺係偮偺曈偺偦傟偧傟傪俁摍暘偟偰,
偦偺岦偐偄崌偆曈偺暘揰摨巑傪捈慄偱寢傇偲,偱偨傜傔側宍偺俋偮偺彫偝偄巐妏宍偵
暘妱偝傟傑偡丅
偙偺偲偒恀傫拞偵偱偒傞彫巐妏宍偺柺愊偼尦偺巐妏宍偺柺愊偺挌搙侾/俋偵側傞偙偲
傪徹柧偣傛丅
彫妛惗掱搙偺抦幆偩偗偱夝偗傞偼偢偱偡丅
偙傟偵懳偟,僸儞僩(hint)偲偟偰懳曈偺暘揰摨巑傪寢傫偱偱偒傞俁偮偺巐妏宍偺偆偪
偺恀傫拞偺偦傟偼慡懱偺侾/俁偵側傞偙偲傪帵偡偙偲偑偱偒傞偲偄偆巜揈傪捛壛偟傑
偡丅
傕偪傠傫,戜宍偱偼側偄偱偡偐傜侾/俁偵側傞偺偼恀傫拞偺巐妏宍偩偗偱椉懁偺巐妏宍
偼侾/俁偵偼側傝傑偣傫丅偙傟偑僸儞僩偱偡丅乿
偙傟偼...TOSHI偺塅拡係
偝傫偐傜偺栤戣偱偡...
捈姶揑偵偼傢偐傞偺偱偡偑...偳偆偟偰傕岻偔尵偊傑偣傫...
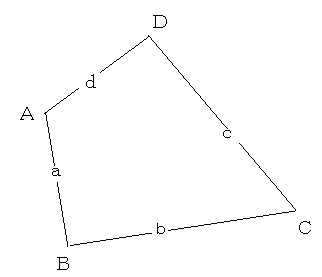
NO.1850丂丂丂嶰妏宍偺捀揰傑偱偺嫍棧偺榓(2) 丂2010.5.4.丂丂栭傆偐偟偺偮傜偄偍偠偝傫
丂丂
乮侾乯
嶰妏宍偺妏偺戝偒偝偲懳曈偺戝彫偲偼堦抳偟傑偡丅
妏偑俙亙俛亙俠側傜丄曈傕倎亙倐亙們偱偡丅
傑偨丄嶰妏宍偺俀曈偺榓偼丄懠偺侾曈傛傝挿偄偱偡丅
丂丂
乮俀乯
嶰妏宍俙俛俠偺撪晹偱奺捀揰傑偱偺嫍棧偺榓偑嵟彫偺抧揰偼丄
惓嶰妏宍俛俠俢偺奜愙墌偲慄暘俙俢偲偺岎揰俤偱偡丅
仸丂崱夞偼偙傟偼僥乕儅偱偼側偄偺偱愢柧偼徣偒傑偡丅
丂丂
乮俁乯
俛俤偲俙俠偺岎揰傪俥偲偟傑偡丅
俠傪拞怱偲偡傞敿宎俠俥偺墌偲俛俥偲偺岎揰傪俧偲偟傑偡丅
慄暘俧俥忋偵揰俫傪庢傝傑偡丅
乮佢俥俫俠亜佢俫俥俠偱偡乯
乮係乯
俙俤亄俛俤亄俠俤亙俙俫亄俛俫亄俠俫偱偡丅
嶰妏宍俙俥俫偵偍偄偰丄俙俫亙俫俥亄俥俙偱偡丅
嶰妏宍俠俥俫偵偍偄偰丄俠俫亙俠俥偱偡丅
偩偐傜丄
俙俫亄俛俫亄俠俫亙俫俥亄俥俙亄俛俫亄俠俥
亖俙俥亄俛俫亄俫俥亄俠俥亖俙俥亄俛俥亄俠俥亖俛俥亄俙俠
傑偨丄嶰妏宍俙俛俥偺撪妏偺偆偪俥偑嵟戝側偺偱丄
俛俥亙俙俛 偩偐傜丄
俛俥亄俙俠亙俙俛亄俙俠
丂丂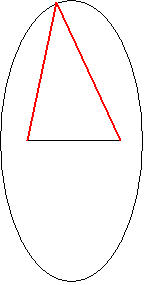
NO.1846偱丄
乽偙傟偑偄偊傟偽...
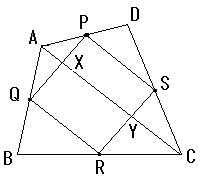
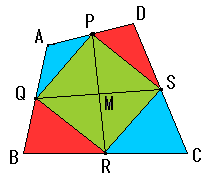
撌巐妏宍ABCD撪晹偵揰 P 傪偲傞偲偒丄AP+BP+CP+DP 偺嵟戝抣傪偲傞偲偒偺揰 P 傕偄偢傟偐偺捀揰偵堦抳偡傞偼偢偱...
偦傟傜偺恾宍偺撪晹偺揰偐奜晹偺揰偐傪昡壙偡傞偲偒嵟挿嫍棧傛傝戝側傜奜晹偲尵偊傞偼偢偩偲...^^?...
堦斒偺撌懡妏宍偺応崌偵傕尵偊傞傛偆側婥傕...? 乿
偲偁傝傑偡偑丄壓慄晹暘偼岆傝偱偡丅
僗儌乕僋儅儞偝傫偺偄偆傛偆偵丄壓偺嶰妏宍偱奺捀揰傑偱偺榓偑嫍棧偺嵟戝偺応崌丄
愒偄曈偺挿偝偺崌寁偑偦偺榓偵側傝傑偡丅
掙曈偺椉抂偐傜偺嫍棧偺榓偑堦掕偲偄偆恾傪偐偔偲懭墌偵側傝傑偡偑偙偺嶰妏宍傪撪晹偵娷傫偱偄傑偡丅
嶰妏宍偺奜晹偱傕嵟戝抣傛傝彫偝側揰偑偁傞偺偼柧傜偐偱偡丅
 乮侾乯
乮侾乯 摨條偵丄
摨條偵丄
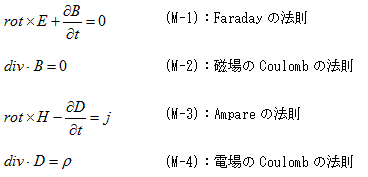
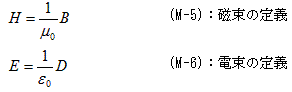
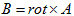 丂丂丂丂丂丂(1)
丂丂丂丂丂丂(1) 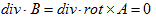
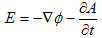 丂丂丂丂丂丂(2)
丂丂丂丂丂丂(2) 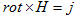 丂丂丂丂丂(1)丗Biot-Savart偺幚尡傛傝捈愙摼傜傟傞Ampare偺朄懃
丂丂丂丂丂(1)丗Biot-Savart偺幚尡傛傝捈愙摼傜傟傞Ampare偺朄懃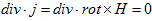
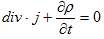 丂丂丂丂丂丂丂丂丂(2)丗揹壸偺曐懚懃
丂丂丂丂丂丂丂丂丂(2)丗揹壸偺曐懚懃
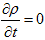 丂丂丂丂丂丂(3)
丂丂丂丂丂丂(3) 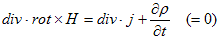
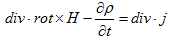 丂丂丂丂丂丂(4)
丂丂丂丂丂丂(4) 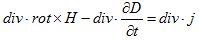
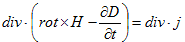
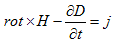 丂丂丂丂丂(M-3)
丂丂丂丂丂(M-3)
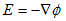 丂丂丂丂丂丂(5)
丂丂丂丂丂丂(5) 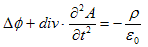 丂丂丂丂丂丂(6)
丂丂丂丂丂丂(6) 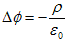 丂丂丂丂丂丂(7)
丂丂丂丂丂丂(7) 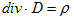 丂丂丂丂丂丂(8)
丂丂丂丂丂丂(8) 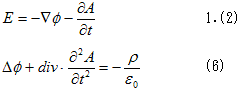
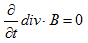 丂丂丂丂丂丂(1)
丂丂丂丂丂丂(1) 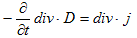
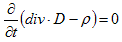 丂丂丂丂丂丂(2)
丂丂丂丂丂丂(2) 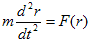 丂丂丂丂丂丂(3)
丂丂丂丂丂丂(3) 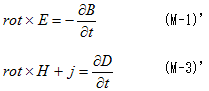
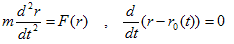
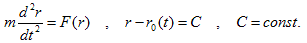
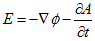 丂丂丂丂丂丂(2)
丂丂丂丂丂丂(2) 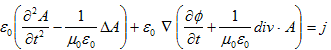 丂丂丂丂丂丂(3)
丂丂丂丂丂丂(3) 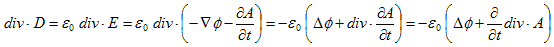
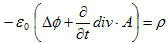 丂丂丂丂丂丂(4)
丂丂丂丂丂丂(4) 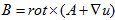
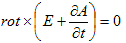 丂丂丂丂丂丂(5)
丂丂丂丂丂丂(5) 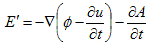
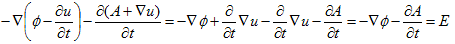
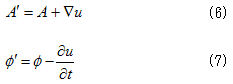
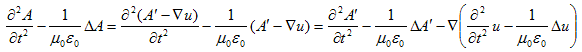
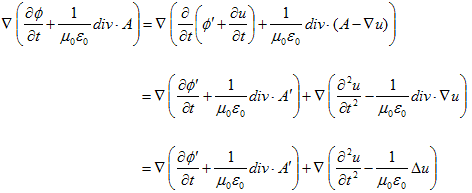
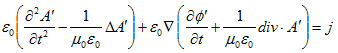 丂丂丂丂丂丂(8)
丂丂丂丂丂丂(8)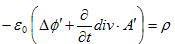 丂丂丂丂丂丂(9)
丂丂丂丂丂丂(9)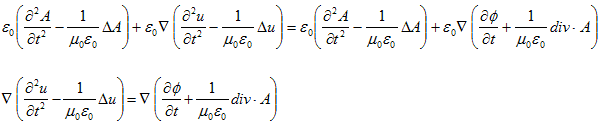
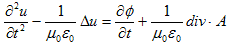 丂丂丂丂丂丂(10)
丂丂丂丂丂丂(10)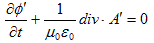 丂丂丂丂丂丂(11)
丂丂丂丂丂丂(11)