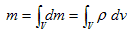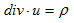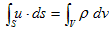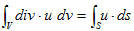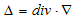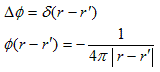NO.1753 ジャリズムの数学 2008.11.22. 浜田 明巳
先日高3理系の生徒に次の問題を解かせてみた.
(1) 10n-1から10n-1までの正の整数で,数字3が使われていないものは何個あるか.
(2) (1)で考えた正の整数の逆数の和は8×(9/10)n-1をこえないことを示せ.
(3) 無限級数1+1/2+1/3+………+1/n+………において,数字3を含む項をすべて除いたとき,新しくえられた級数の和は80をこえないことを示せ.
解答は次のようである.
(1) 問題の整数はn桁の正整数である.
3を使わないn桁以下の非負整数の個数は,9n個.故に3を使わないn桁以下の正整数の個数は,0の1個を引いた,9n-1個.
同様に3を使わないn-1桁以下の正整数の個数は,9n-1-1個.
故に3を使わないn桁の正整数の個数は,
(9n-1)-(9n-1-1)=(9-1)9n-1=8・9n-1(個)
(2) (1)の数で最小のものは,10n-1.故に逆数で最大のものは,1/10n-1.
逆数の和をSnとすると,
Sn≦8・9n-1・1/10n-1=8・(9/10)n-1
(3) (2)から,求める級数の和は,
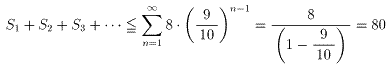
解答はこれで終わりであるが,これの数学的意味をこう教えた.要するに∞を扱うときには直観通りにはならない場合があるという事を,分かりやすく教えようというのである.
芸人ジャリズムの1人の,1から数を数えるとき,3の倍数と3がつく数字を言うときにアホになる,というギャグが流行っている(流行っていた?).
教育的見地から,これはあまり好ましい事ではないらしい.特に小学校低学年児や幼稚園児にとっては,3のつく数字は理解出来ても,3の倍数については分からないので,1,2以降のすべての数において全員アホになる(叫ぶ)という大変教室が騒がしい状況になっているというのだ.かろうじて高学年くらいになれば算数指導において,いい教材になると思うのだが,そうはうまくはいかないだろう.
それを踏まえて,実際の授業でこのように話をしてみた.
とりあえず3の倍数はさておき,3のつく数字のみで考える.以前の授業で
1+1/2+1/3+………+1/n+………=∞
となる事を何通りかの方法で指導した(※).ところが3のつく数字の逆数を取り除くだけで80以下の数となり,発散しなくなるのだ.3のつく数字がいかに沢山存在するか分かるだろう.ましては,3の倍数まで取り除くのだから.
試しに1000の倍数のみを残したくらいでは,
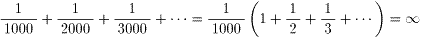
と∞になるのだ.
実際テレビのその芸人の1から40までを数える姿をよく見てみよう.1から29まで数えるのはそんなに苦労がないが,30から39まではすべてアホになり,40でやっとまともになって,終わる.その40を言った後の芸人の疲れ切った姿を見てみれば,それが3のつく数字の多さの証拠となるのだ! さらに30の段だけでなく,300の段,3000の段,30000の段と沢山あるのだから.
途中生徒からの「じゃあ,先生やって見せて」というヤジを無視しながらこの話をしたときの生徒の反応は,それなりのものがあった.普段黙々と問題を解いているのみの私からは想像も出来ない話が出て来たので,びっくりした面もあっただろう.受験勉強の為本当にテレビも何も見ずに過ごしている生徒にはまったく何の事か分からずじまいだったかも知れない.しかしほとんどの生徒の顔はニヤついていたので,印象深く思ってはくれたらしい.∞の計算は直観的にはいかない場合があると分かってくれた事を望んでいる.
その後の指導として,次の事まで話を進めればよかったかも知れない,と反省している.
9・10n-1個あるn桁の整数の中で,3を使わないn桁の整数は8・9n-1個あるので,割合は,
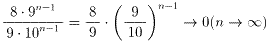
となるので,(3)のような事がいえると思われる.
(※)
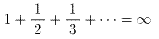 の証明
の証明
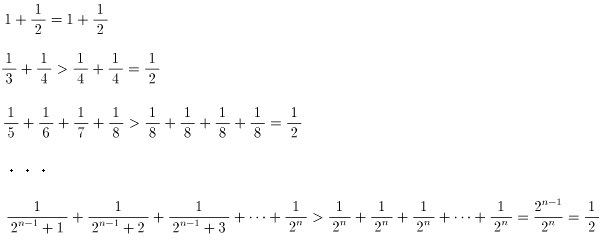
辺々を加えると,
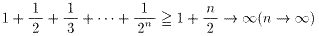
∴ 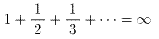
(別解) 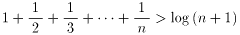 を示す.
を示す.
k>0のとき,y=1/xのグラフのk<x<k+1の部分を考えると,
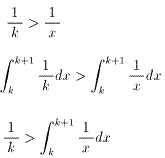
k=1,2,3,………,nを代入して,辺々を加えると,
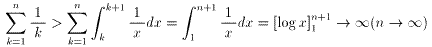
∴ 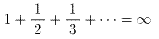
NO.1752 ベクトル解析Minimum(3) 2008.11.17. DDT
ベクトル解析Minimum-1,2の続きです。
Minimum-1では、ポテンシャルφと∇とdiv を扱いましたが、この3つとベクトル作用素rot は、切っても切れない縁があります。
ここではベクトル解析Minimum-2の章番をそのまま引き継ぎますが、
ベクトル解析Minimum-1,2の式を参照する場合は、V-1.3.(6),V-2.5.(11)などと書きます。
6.偏微分の順序交換とrot,保存場,積分記号下の微分
V-1.1.では、全微分の式を導く前段階として、V-1.1.(5)、
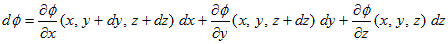 (1)
(1)
を得ました。V-1.1.では、(dx,dy,dz) が微小な事を考慮して、(dx,dy,dz)→(0,0,0) の極限を考えましたが、ここではそうせずに、(1)の微分(線形化)をさらに進めます。例えば(1)の右辺第1項は、
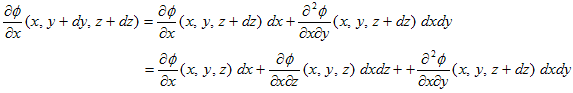
と線形化できます。これに対して、(dx,dy,dz)→(0,0,0) を考慮すると、
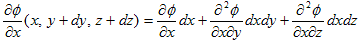
となります。2項目に同じ事をすれば、
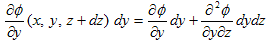
となります。よって2回目の線形化(2階微分)によって、(1)は、
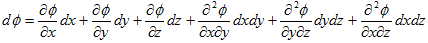 (2)
(2)
と書けます。(1),(2)を得る際の(x,y,z) の変化の経路に注意します。(1),(2)を得た経路は、
(x,y,z)→(x,y,z+dz)→(x,y+dy,z+dz)→(x+dx,y+dy,z+dz)
というものです。しかし、次の3つの経路も可能です。
(x,y,z)→(x,y,z+dz)→(x+dx,y,z+dz)→(x+dx,y+dy,z+dz)
(x,y,z)→(x,y+dy,z)→(x,y+dy,z+dz)→(x+dx,y+dy,z+dz)
(x,y,z)→(x+dx,y,z)→(x+dx,y+dy,z)→(x+dx,y+dy,z+dz)
このとき、それぞれの変化経路で得られる、(2)に相当する線形化は、
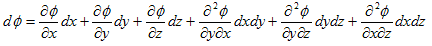 (3)
(3)
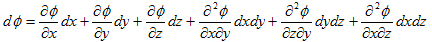 (4)
(4)
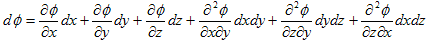 (5)
(5)
となります。一方、φの増分dφは、φ=φ(x,y,z) である事から、(x,y,z) → (x+dx,y+dy,z+dz) という変化だけで決まるはずで、変化経路には依存しないはずです。従って、(2)=(3),(2)=(4),(2)=(5) とおけて、そのそれぞれより、
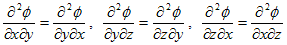 (6)
(6)
が出てきます。(6)を、多変数関数の偏微分の順序交換と言います。同様な考えを繰り返し用いれば、何階の偏微分に対しても、偏微分の順序は交換可能である事もわかります。もちろん必要な階数分、偏微分可能としてですが。(6)の状況を、2次元の場合に述べたのが、次の図です。
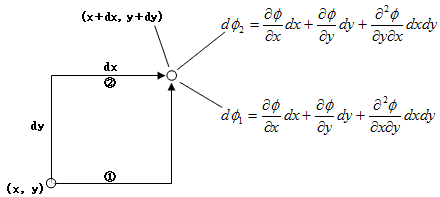
右図のように、二つの経路①,②で、(x,y) を (x+dx,y+dy) まで変化させた時のφの増分は、(6)が成り立つなら、dφ1=dφ2です。これはφ(x,y) の値が、位置(x,y)のみで決まる事からも明らかです。
そうでない場合、φの値は(x,y) のみでは決まらず、φの増分は(x,y) の変化経路に依存する事になります。
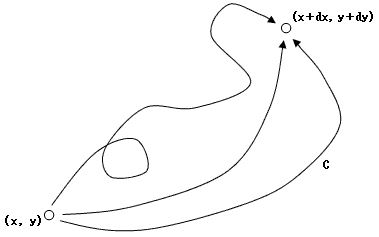
逆に、流速u=(vx(x,y,t),vy(x,y,t)) があり、ある固定した時間tにおいて、(x,y) から (x+dx,y+dy) までの流速の、任意の経路に沿った積分が、
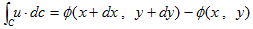
のように、経路に依存せず、位置(x,y),(x+dx,y+dy) のみで決まるなら、位置のみで決まるスカラー関数φ(x,y) が存在する事になり、再び(6)が得られます。この場合、(dx,dy) が微小である必要はありません。また、上記線積分で、C は任意の経路を表しており、dc はその接線ベクトルです。
もしφ(x,y) が存在するなら、(dx,dy) を再び微小とし、
(x,y) → (x+dx,y)
(x,y) → (x,y+dy)
という変化を考えて、
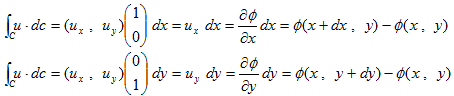
という関係から、
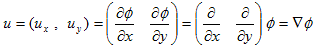
が得られるので、φは流速uの速度ポテンシャルになります。要するに、
(6) ⇔ u=∇φ
が言えます。
関係(6)をカッコ良くするために、×をベクトル間の外積として、次のベクトル作用素rot を定義します。
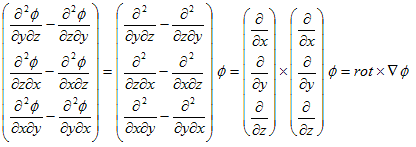 (7)
(7)
ベクトル作用素rot の実体も∇ですが、外積×を通じてベクトルに作用する∇は、rot と書くのが慣わしです。よって、
速度ポテンシャルφが存在する ⇔ u=∇φ ⇔ rot×u=0
が言えます。
(7)が0かどうかは、φの性質によって決まります。
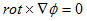
が成り立つとき、-∇φをポテンシャルφから導かれる保存場と言います。さらに、φがポテンシャル(空間の位置のみで決まる関数)であるとわかっている時は、
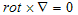 (8)
(8)
は、ベクトル解析の公式です。
最後に、積分記号下の微分を導きます。以下の導出は、適当な条件下でしか成立しませんが、積分記号下の微分は、ほとんど恒等式である事がわかります。
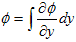
は恒等式です。よって、
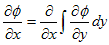
ですが、
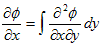
も恒等式です。従って、

が得られます。
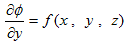
なので、fにおきかえると、
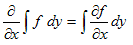
となって、積分記号下の微分が得られます。同様に、
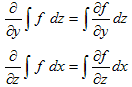
も導けます。
NO.1751 博士の愛した数式 2008.11.17. 水の流れ
問題6 一部修正 11月20日
第216回数学的な応募問題
皆さん、エレガントな解き方をしてみませんか。
問題1
下の図は、いずれも2次関数y=ax2+bx+cのグラフです。
それぞれのa,b,cの符号をいえ。
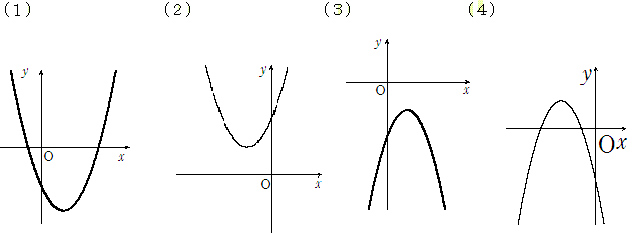
問題2
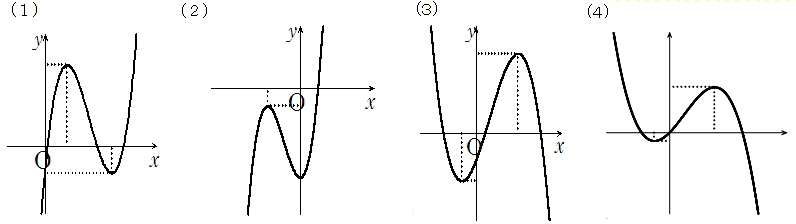
下の図は、いずれも3次関数y=ax3+bx2+cx+dのグラフです。
それぞれのa,b,c,dは正、負、0かをいえ。
問題3
関数f(x)=x3+ax2+bx+cについて
(1)x=1で極大となる条件を求めよ。
(2)x=-2で極小となる条件を求めよ。
問題4

問題5
を証明せよ。
問題6
小川洋子さんが書いた「博士の愛した数式」という本を読んだことがありますか。
映画にもなっていました。数学史上最も美しいといわれている等式 eiπ+1=0 を証明してください。
問題7
さて、ii はどんな数か近似値を求めよ。
問題8
オイラー(1707~1783)が上の定理を考え出したのは1741年12月頃に出したゴールドバッハへの手紙からです。(この文は「数学セミナー2006年2月」に掲載された東工大教授黒川信重氏の記事から引用) それでは、下にあるドモアブルの定理から nを無限大にして極限をとって導いてください。
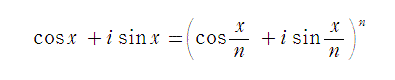
注:この記事に関する投稿の掲載は、2008年12月8日以降とします。
NO.1750 アイゼンスタイン三角形(2) 2008.11.17. 夜ふかしのつらいおじさん
問題1
a=m2-n2,b=2mn+n2,
c=m2+mn+n2
| m | n | a | b | c | a+b | 積 | 840で割った商 |
|---|
| 2 | 1 | 3 | 5 | 7 | 8 | 840 | 1 |
| 3 | 1 | 8 | 7 | 13 | 15 | 10920 | 13 |
| 3 | 2 | 5 | 16 | 19 | 21 | 31920 | 38 |
| 4 | 1 | 15 | 9 | 21 | 24 | 68040 | 81 |
| 4 | 2 | 12 | 20 | 28 | 32 | 215040 | 256 |
| 4 | 3 | 7 | 33 | 37 | 40 | 341880 | 407 |
問題2
a=m2-n2,b=2mn+n2,
c=m2+mn+n2より
a2+b2+ab
=(m2-n2)2+(2mn+n2)2
+(m2-n2) (2mn+n2)
=m4-2m2n2+n4+4m2n2
+4mn3+n4+2m3n+m2n2-2mn3-n4
=m4+m2n2+n4+2m3n+2mn3+2m2n2
=(m2+mn+n2)2
=c2
問題3
840=23・3・5・7 です。
abc(a+b)
=(m2-n2) (2mn+n2)
(m2+mn+n2) (m2-n2+2mn+n2)
=mn(m+n) (m-n) (2m+n) (m+2n) (m2+mn+n2) です。
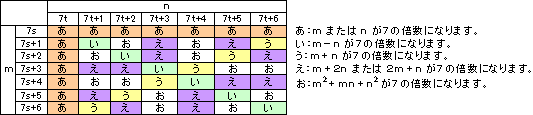
(1)2の因数
・m,nが互いに素なので、ともに奇数の場合を考えます。

・m,nの一方が偶数で他方が奇数の場合を考えます。
仮にmが偶数、nが奇数とします。(反対のときも同様に考えられます)

(2)3の因数
m,nを3を基準にして分類します。

(3)5の因数
m,nを5を基準に分類します。

(4)7の因数
m,nを7を基準に分類します。
問題4
c2=a2+b2+ab ・・・(1)
a=A2,b=B2 とおくと、
c2=(A2)2+(B2)2+(AB)2 ・・・(2)
(右辺は、3数の平方和)
次の恒等式を考えます。
(m+n+p)2=m2+n2+p2+2(mn+np+pm) ・・・(3)
右辺の太字の2次の基本対称式部分が 0 となれば、(2)の式と同じ形になります。
mn+np+pm=0 とすると、p=-mn/(m+n)
これを(3)に代入すると
{m+n-mn/(m+n)}2=m2+n2+{-mn/(m+n)}2
両辺に (m+n)2 をかけると、
{(m+n)2-mn}2={m(m+n)}2
+{n(m+n)}2+(mn)2
(m2+mn+n2)2=(m2+mn)2
+(mn+n2)2+(mn)2 ・・・(4)
(4)の形のままでは(2)を満たすような整数A,Bが見つかりません。
そこで右辺を変形します。
(右辺)
=(m2+mn)2+(mn+n2)2+(mn)2
=m4+2m3n+3m2n2+2mn3+n4
=(m4-2m2n2+n4)+(4m2n2+4mn3+n4)
+(2m3n+m2n2-2mn3-n4)
=(m2-n2)2+(2mn+n2)2
+(m2-n2) (2mn+n2)
∴
(m2+mn+n2)2
=(m2-n2)2+(2mn+n2)2
+(m2-n2) (2mn+n2) ・・・(5)
この結果と(2)の、式を比べて
a=A2=m2-n2
b=B2=2mn+n2
c=m2+mn+n2
この問題は答が分かっているので、強引にその形を作りました。
また、(4)より、mとnについて対称なので、上の答のmとnの入れ替えをしたものも答になります。
NO.1749 ベクトル解析Minimum(2) 2008.11.8. DDT
ベクトル解析Minimum-1の続きです。個人的意見では、δ関数の取り扱いは実用上、その目的意識からしてベクトル解析と不可分のものです。
ここではベクトル解析Minimum-1の章番をそのまま引き継ぎますが、ベクトル解析Minimum-1の式を参照する場合は、V-1.3.(6)などと書きます。
5.δ関数(デルタ関数)とラプラス方程式の基本解
V-1.4.において当初、蛇口による湧き出しというものを考えましたが、蛇口による湧き出しは、V-1.4.(6)、
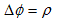 (1)
(1)
にとって、本来は非常に取り扱いにくいものです。(1)は、非圧縮性渦なし完全流体の支配方程式で、今でも色々な場面において、Newtonの運動方程式と同等くらいの重要さがあります。なぜ蛇口による湧き出しが問題かと言うと、(1)の右辺のρが、湧き出し密度だからです。
実際に観測できるのは、もちろん秒当たり何m3の水が出てくるかの、湧き出しの方です(m3/s)。では何故、単位体積(単位面積)当たりの湧き出し密度(m3/s/m3=1/s)なんてものを定義したのでしょう?
どんな蛇口の分布になっているか、実際のところ、事に当たるまでわからないからです。それでどのような場合にも対処できる定式化として、湧き出し密度分布を定義し、(1)を考える事になります。
しかし密度は、体積をかけるまで本当の湧き出し量にはなりません。これは、質量密度が体積をかけるまで本当の質量にならないのと同じ事情です。ところが蛇口の湧き出しとは、一点の湧き出し密度によって、それがそのまま湧き出し量になるのですから、湧き出し密度の言葉としては、「無限大の湧き出し密度だ!」と言わざる得ません。無限大はふつう、数学的処理の範囲外です。そのような問題が、Newtonの運動方程式と同等くらいの重要さがあると思われる(1)に、含まれている事になります。現実に蛇口はあるのですから。
さらに悪い事に、分布する蛇口という状況を平均化して得られた概念が、まさに湧き出し密度の出自である事は明らかなので、蛇口的湧き出しは、湧き出し密度の概念内で解決するのが望ましい懸案事項になります。これは長年の夢でした。そしてそれに解決を与えたのが、Dirac(ディラック)のδ関数(デルタ関数)です。
δ関数は、初等的には次のように定義されます。3次元の位置ベクトルをrで表わす事にします。原点r=0に特異点を持つδ関数とは、以下です。
1) δ(r),r≠0 については、δ(r)=0.
2) δ(0)=∞.ただしこ
の ∞ は、次の3)で規定される.
3) r=0 を内部に含む任意の領域Vで、
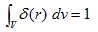
が成り立つ.
このようにδ関数を定義すると、本当に、δ関数はいい加減なものに見えますが、大丈夫です。この定義の背後には、矛盾のないしっかりした数学理論が控えています。それがかの超関数ですが、「ベクトル解析Minimum」の趣旨により、その説明は控えます(本当はできないから(^^))。実用上は、1)~3)の使い方をおぼえるだけで十分です。またδ関数は、実用的に使うために考え出されたものです。こんな例は、どうでしょう?
静止した物体,質量m(kg)が、t=0 の瞬間にハンマーに叩かれて1(m/s)で走り出す、という例です。このとき物体mは、t=0 の瞬間に運動量m(kgm/s)を与える無限大の撃力を受けた、と言います。

これの最も単純な扱いは、t=0 での初期条件に初速1(m/s)を与えて、後は力=0 の運動方程式を解く、というものです。結果は解くまでもなく、t<0で静止,0≦tで1(m/s)の等速運動 です。しかし初見で上記問題に当たると、こんなに簡単な事さえ思いつけない時があります。やはりこの解き方は、概念として難しいのです。一方、δ関数を使うと、直接、運動方程式を書けます。
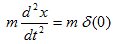 (1)
(1)
(1)は簡単に解けます。まず0<t で考えると、δ関数の性質1)より、
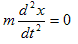
です。ただちに積分して、
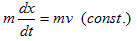 (2)
(2)
を得ます。0<t では等速運動です。では v の値は? それはt=0 での運動量の値を調べればわかります。
(2)は(1)を、0<t の範囲で積分した結果でした。
今度はt=0 を含む区間 [-ε,ε],ε>0 で積分します。δ関数の性質2),3)より、
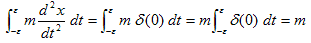 (3)
(3)
を得ますが、(2)と(3)の積分区間、(0,∞) と [-ε,ε] は、(0,ε] で重なっています。(0,ε] で(2)と(3)は一致しなければなりません。従って、
mv=m
すなわち、
v=1
となります。0≦t で1(m/s)の等速運動です。ここで mδ(0) が、t=0 の瞬間に瞬間的に作用し、有限の運動量m(kgm/s) を与える無限大の撃力を表わしている事は、(1)と、δ関数の性質1),2),3) から明らかだと思います。そして力とは時間に関する、運動量密度だと言えます。
δ関数を使う方法は、初速を1(m/s) と与える方法より確かに手がかかります。かかりますが、処理手順の自体は何も考える必要がありません(慣れてくればですが)。初速を1(m/s) と考える方法では、初速は1(m/s) だと、まさに「考え付く」必要がありますが、δ関数の処理は機械的なものです。δ関数を使う方が、概念的には遥かに易しいと思いませんか?。そしてこのケースでの両者の差は、V-1.1. で似たような議論をした時ほど僅かな差ではないと、自分には思えます。さらにδ関数の考えは、このケースより遥かに複雑な問題にも適用可能です。そのような場合、「考え付く必要がある」やり方では、対処できないかも知れません。
以下では、ラプラス方程式の基本解、すなわち、
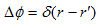 (4)
(4)
を満たすスカラー関数φを計算します。すなわち、蛇口的湧き出し問題の解決です。ここでδ(r-r') は冒頭に定義したδ関数をr' だけ平行移動したもので、r' に特異点を持つδ関数と言われます。
(4)でまず、再びr'=0 としても良いことは明らかです。直上で言ったように、(4)の解に戻すには、r'≠0 だけ平行移動するだけです。そこで、
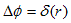 (5)
(5)
とします。
(5)を解くに当たっては、δ関数の等方性に注意します。等方性とは要するに、δ関数には特徴的な性質を示す特定の方向は存在しない、という事です。いま特異点はr=0 で原点にあります。
δ関数の性質1)は、r≠0 で δ(r)=0でした。特異点はr=0 にある事から、
この性質に特別な方向性はありません。
次に2)では、δ(0)=∞ です。これはr=0 という一点に関する性質なので、
やはり方向性はありません。
3)については、こうなります。r=0 を内部に含む任意の領域Vが、どんなに無茶苦茶な形をしていても、
その中には常に、r=0 をその中心とする、閉球または閉円板V'が存在します。
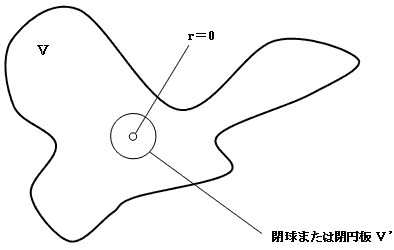
従って1)を考慮すると、
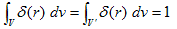
となり、Vがどんな形であろうと、3)の性質は、等方的な形状を持つV'で
の積分で決定される事がわかります。よって性質3)にも、方向性はありません。δ関数δ(r)は、特異点(今はr=0)に関して、等方性を持つ関数だったのです。
次に Δφ=δ(r) は偏微分方程式です。つうじょう偏微分方程式を解く場合には、
有限の解析領域を定め、解析領域の境界に境界条件を与えます。境界条件が必要なのは、
解析領域内部の解は、領域内部の事情(今の場合、それはδ(r))の他に、
領域外部の影響も受けるからです。逆に言うと、解析領域を全空間とし、境界条件を与えなければ、
δ(r)の影響のみによる解が、全空間に対して得られます。いま求めたい基本解とは、そのようなものです。
そうするとδ(r)には、特異点に関する等方性があったので、φも等方的な解になります。
そのような解を計算するために、球面極座標に移ります。
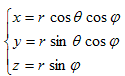 (6)
(6)
ここでrは原点からの距離を表わし、θが2次元(x,y)の極座標成分を、ψがzに関する極座標成分を負担します。0≦θ<2π,-π≦ψ≦πです。(6)を用いて、Δの極座標表示を計算します。この計算は長いですが、一回でも完全にやると納得できるものなので、やる事にしました。
まず(6)の各式をx,y,zで偏微分します。
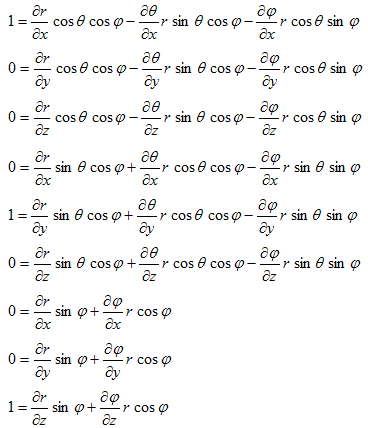
得られた9本の式を、xでの偏微分,yでの偏微分,zでの偏微分にグループ分けすると、
次の3つの連立方程式の系が得られます。
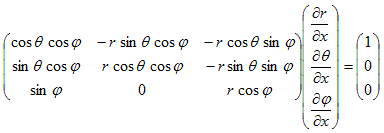 (7)
(7)
 (8)
(8)
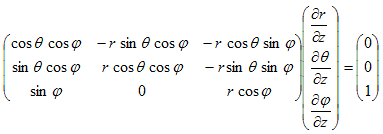 (9)
(9)
(7)~(9)の目的は、Δ(x,y,z) を Δ(r,θ,ψ) に書き換えるために必要な、(∂r/∂x,∂θ/∂x,∂ψ/∂x),(∂r/∂y,∂θ/∂y,∂ψ/∂y),(∂r/∂z,∂θ/∂z,∂ψ/∂z) の9成分を、(r,θ,ψ) の表式として得る事です。(7)~(9)を直接解いてもそれらは得られますが、余りにも大変なので、次の事に注意します。
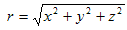
です。これを、(6)を考慮しながら、xで偏微分すれば、
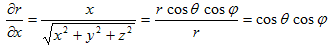 (10)
(10)
となります。上記を、(7)の3行目に代入する事により、
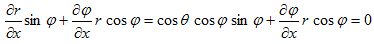
が得られます。よって、
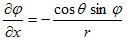 (11)
(11)
となり、(10)と(11)を、(7)の1行目または2行目に代入すれば(2行目に代入しました)、
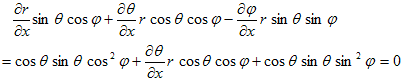
すなわち、
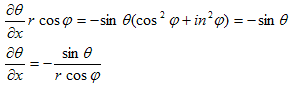
となります。以上まとめれば、
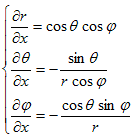 (12)
(12)
を得ます。同様に、
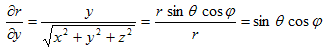
なので、(8)の3行目に代入すれば、
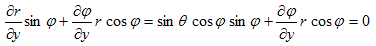
すなわち、
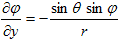
で、
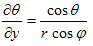
となり、
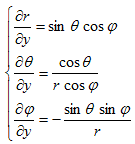 (13)
(13)
です。zについては、
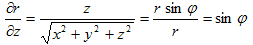
なので、(9)から、
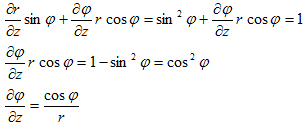
となり、
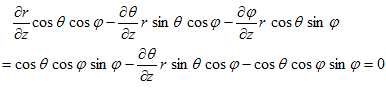
から、
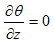
です。従ってまとめると、
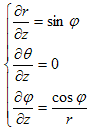 (14)
(14)
となります。
(12),(13),(14)を用いて、Δ(x,y,z) を Δ(r,θ,ψ) に書き換えます。そのためにφ(x,y,z) は、すでにφ(r,θ,ψ) に書き換えられているとします。よって、(r,θ,ψ) は(6)を介して、(x,y,z) の関数として与えられている事になります。具体的にそれらを(6)から計算する事も可能ですが、ここではそれは行いません。つまり、
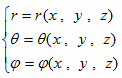 (15)
(15)
という事であり、
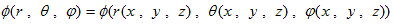 (16)
(16)
という事でもあります。(15),(16)のもとでは、(12)より、
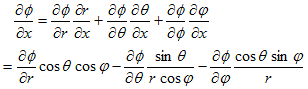
が得られます。従って、微分作用素の関係としては、
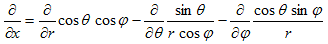
です。同様に、
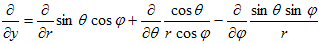
であり、
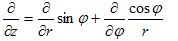
が得られます。これらを、
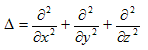
に適用すれば、
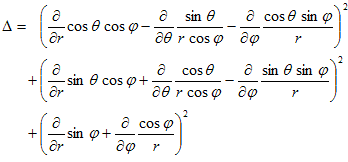 (17)
(17)
となるのですが、(17)の計算は、無茶苦茶大変そうです(実際大変です)。でも今欲しいのは、(5)を満たすような等方的な解です。それはφ=φ(r) と同じ事です。従って(17)において、∂φ/∂θや∂φ/∂ψになる部分は 0、とおける事がわかります。
この条件を使うと、
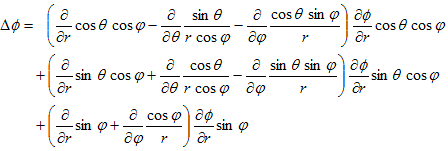
となり、いくらか楽にはなりますが、この先の計算もまだまだ大変なので、結果だけ述べます。
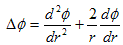
と、信じられないくらい綺麗な形にまとまります。よって(5)より、ラプラス方程式の基本解の支配方程式は、
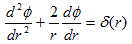 (18)
(18)
です。(18)は、(1)と同じ手順で解く事ができます。最初にr≠0 で考えれば、
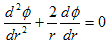
です。これは線形常微分方程式で、解の公式があります。適用すると、
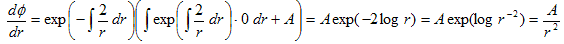
が得られるので、もう一回積分し、
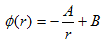 (19)
(19)
となります。ここでA,Bは積分定数で、(19)を導いた積分領域は、原点を除いた全空間Eです。
A,Bを定めるために、(18)を、半径ε>0 の閉球Vで積分します。δ関数の性質より、
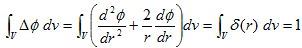 (20)
(20)
です。同じ積分を、(19)に対して行います。このとき、ベクトル解析の公式 Δ=div・∇ と、Gaussの発散定理を考慮します。
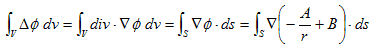 (21)
(21)
(21)のSは、半径εの球面で、dsはその面素ベクトルなので、Sの面素をda,外法線単位ベクトルをnとすれば、ds=danとおけます。nは球面極座標の定義(6)で、r=1 とおけば得られます。
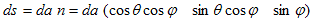 (22)
(22)
また、再度(6)を考慮する事により、
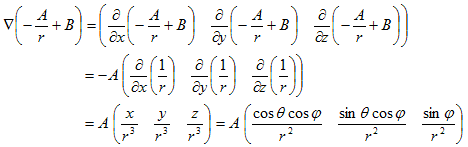
ですが、上記が半径εの球面上に束縛されたベクトルである事と、(22)に注意すると、
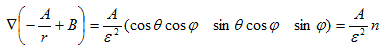
であるのがわかります、よって(21)は、n・n=1 なので、
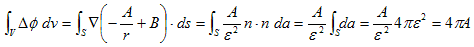 (23)
(23)
となります。何故なら、∫S da が半径εの球の表面積を表わすのは、明らかだからです。しかし(23)と(20)は、一致しなければなりません。何故なら、(23)の被積分関数(19)を導いた積分領域Eと、(20) を導いた積分領域Vは、原点を除いたV全体で重なっているからです。従って、
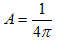
と決まります。最後にBの扱いですが、Bは(18)の右辺に、何も寄与していないのがわかります。もし寄与するなら、(23)と(20)が一致する事から、(23)の最右辺にBを含む項があるはずですが、ありません。よってBは、δ(r)の影響を表わしたものではないと判断できて、B=0 とおけます。
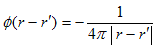 (24)
(24)
が、ラプラス方程式の基本解です。ここでrを再びベクトルと考え、解をr'≠0 だけ平行移動しました。
(24)の形が手に入ると、任意の湧き出し密度分布ρ(r) に関するポアソン方程式、
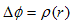 (25)
(25)
の形式解は、いともたやすく導けます。それにはラプラシアンΔの線形性(重ね合わせが効く、とも言います)を使います。ラプラシアンΔの線形性とは、Δφ1=ρ1とΔφ2=ρ2 を満たす(25)の解と、任意の実数kについて、「φ1+φ2 は Δ(φ1+φ2)=ρ1+ρ2 を満たす」、かつ「kφ1 は Δ(kφ1)=kρ1 を満たす」というΔの性質です。この事実は、Δを(x,y,z) で書いた場合を考えれば、すぐわかります。
最初に、
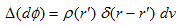 (26)
(26)
を考えます。(26)のρ(r')δ(r-r')dv は、無限大の単位湧き出し密度δ(蛇口)に、まともな湧き出し密度ρ(r') で決まる、微小なその点の湧き出し量ρ(r')dv をかけて薄めたものなので、湧き出し密度ρ(r') と同等だとみなせます。
空間内にρ(r') 唯一点の湧き出し密度しかないとすると、(26)の解は「kφ1 は Δ(kφ1)=kρ1 を満たす」の考えを使って(24)より、
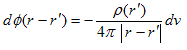 (27)
(27)
です。ρ(r') がそこら中にあるとします。それならば、「φ1+φ2 は Δ(φ1+φ2)=ρ1+ρ2 を満たす」の考えを用いて、(27)を重ね合わせるだけです。実際には考えている体積Vでの、(27)の合計をとります。
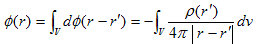 (28)
(28)
(28)は、体積Vに外部条件がない場合の(体積Vの内部の湧き出し密度分布ρだけで解が決まる場合の)、(25)の解です。これは古典的には、グリーン関数の方法と言われますが、こうして微小質量を用いた、機械的な質量密度からの質量の計算法、
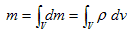
が再現されます。つまりδ関数の導入によって、次の事が実現されます。
④ 密度の概念はいつも有効になり、微小要素を用いた直感的計算を、首尾一貫して行えるようになる.
この節と以前の結果とを合わせると、次のようになります。
ベクトル解析が使われる理由は、
① ベクトル記法によって、微小要素部分とそうでない部分とを分離する.
② ベクトル記法によって、複雑な式の判読が容易になる.
③ 式を見ただけで、物理的イメージが沸く.
でした。④に関しては、①の関連が重要です。①を導入したのは、微小要素を用いた直感的計算を行いたいという目的意識があったからでした。ところがそれは、常に密度という概念を導き、それは一点に集中した何かという、実際に存在する物理的現実と相性の悪いものでした。それを技術的に解決するものが、δ関数と④です。従って、以下の組み合わせは、物理には頻繁に出てきます。
・ポテンシャルφの勾配、∇φ
・保存則
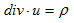
または、
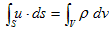
・ Gaussの発散定理
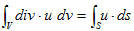
・ ベクトル解析の公式
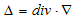
・ ラプラス方程式の基本解
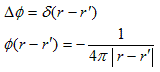
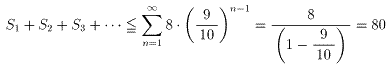
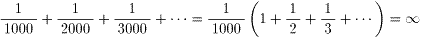
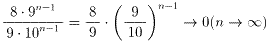
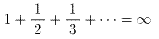 の証明
の証明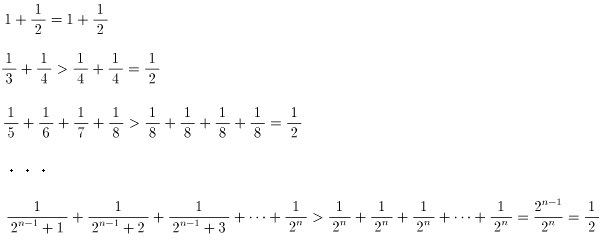
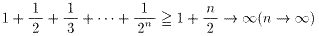
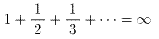
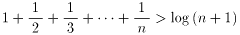 を示す.
を示す.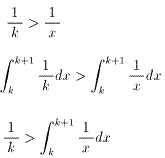
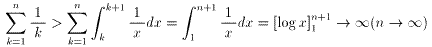
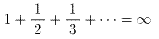
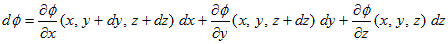 (1)
(1)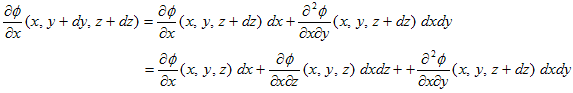
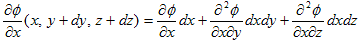
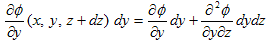
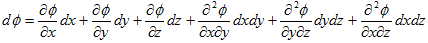 (2)
(2)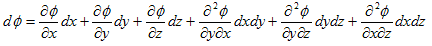 (3)
(3)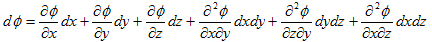 (4)
(4)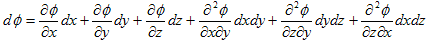 (5)
(5)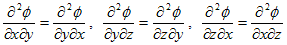 (6)
(6)

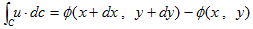
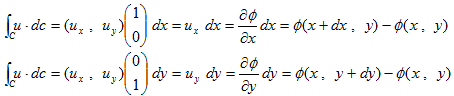
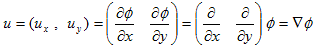
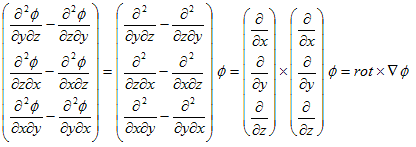 (7)
(7)
 (8)
(8)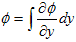
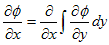
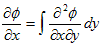

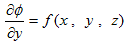
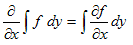
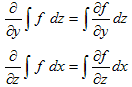
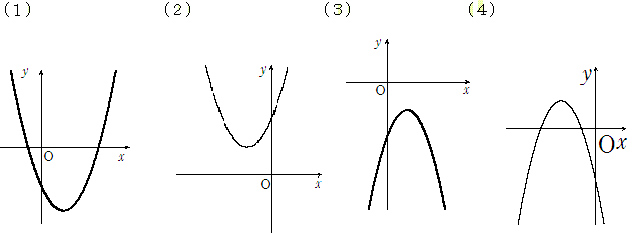

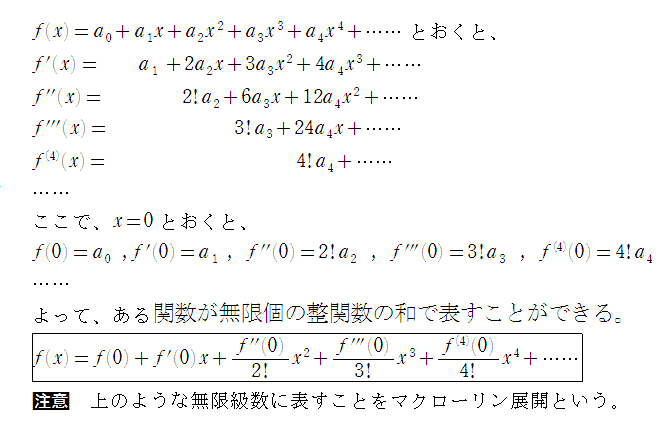

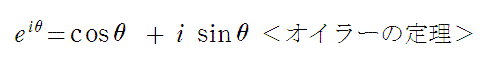
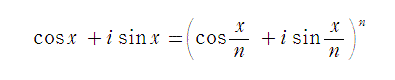





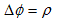 (1)
(1)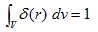

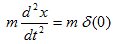 (1)
(1)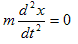
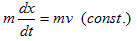 (2)
(2)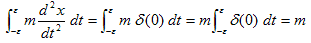 (3)
(3)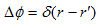 (4)
(4)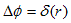 (5)
(5)
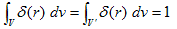
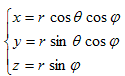 (6)
(6)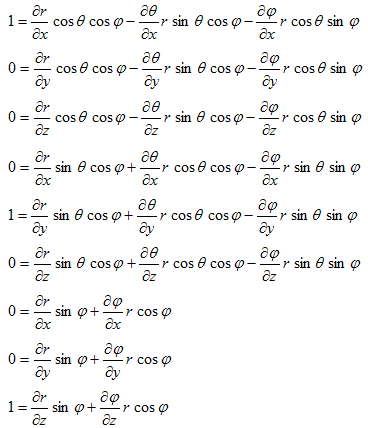
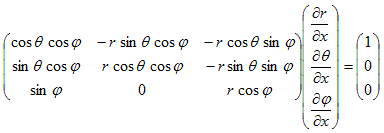 (7)
(7) (8)
(8)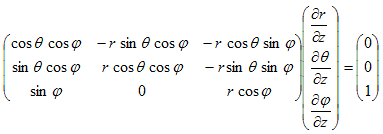 (9)
(9)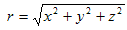
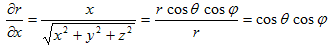 (10)
(10)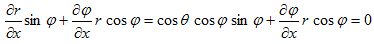
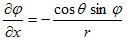 (11)
(11)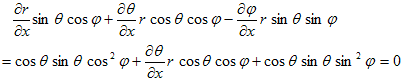
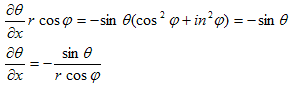
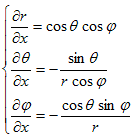 (12)
(12)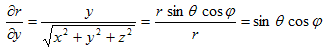
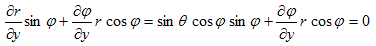
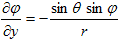
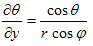
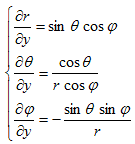 (13)
(13)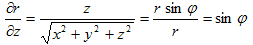
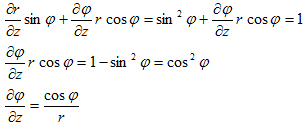
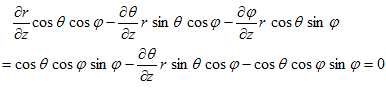
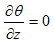
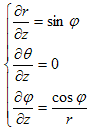 (14)
(14)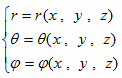 (15)
(15)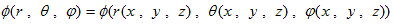 (16)
(16)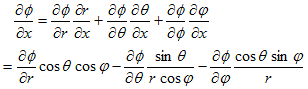
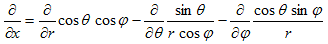
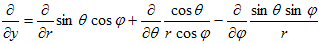
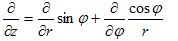
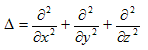
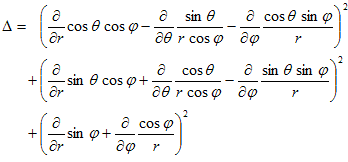 (17)
(17)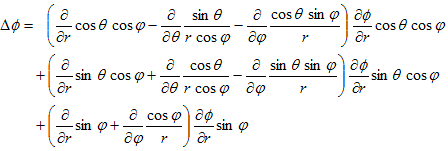
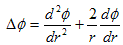
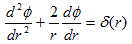 (18)
(18)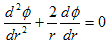
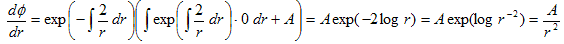
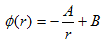 (19)
(19)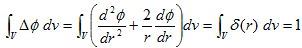 (20)
(20)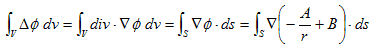 (21)
(21)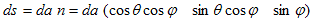 (22)
(22)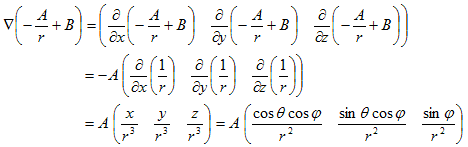
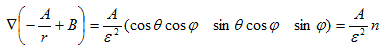
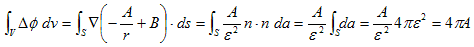 (23)
(23)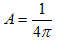
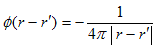 (24)
(24)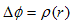 (25)
(25)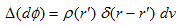 (26)
(26)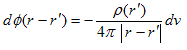 (27)
(27)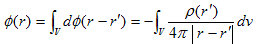 (28)
(28)