NO.1849 両皿天秤のオモリ(2) 2010.4.24. 夜ふかしのつらいおじさん
エレガントな解答はないように思います。
両皿天秤のオモリの問題ですが、お金の支払いの問題として考えます。
その方が分かりやすい気がします。
まず、基本的なことを見ておきます。
● おつりをもらわないで支払いをするなら、{1,2,4,8,16}円硬貨を使います。
2進法で数を表すことを考えれば理解できます。
1円から、1+2+4+8+16=31円までもれなくだぶりなく支払えます。
1枚の硬貨は{使う,使わない}の2通りです。
だから、25=32より、0円のときを除いて31通りです。
1円を支払うのに、1円硬貨を使います。
2円を支払うのに、2円硬貨を使います。
3円を支払うのに、1円硬貨と2円硬貨を使います。
4円を支払うのに、4円硬貨を使います。
・・・
硬貨の種類を、金額が小さい順に増やすことを考えます。
持っている硬貨を全部使って支払えない最小の金額の硬貨があれば良いことになります。
● おつりをもらうことができるのならば、{1,3,9,27,81}円硬貨を使います。
買い物をする人とお店にこの金額の硬貨があれば、121円までもれなくだぶりなく金額の支払いができます。
仕組みを、{1,3,9}の簡単な場合で説明します。
買い物をする人とお店にこの金額の硬貨があれば、13円までもれなくだぶりなく金額の支払いができます。
3の倍数は次のように表せます。
「+」は支払い、「-」はおつりと考えます。
3=3, 6=9-3, 9=9, 12=9+3
自然数は、{3n,3n+1,3n-1}のどれかの形をしています。
上のように、1円以外の硬貨ですべての3の倍数の金額を表すことができます。
1円硬貨を支払えば3n+1円、1円硬貨でおつりをもらえば3n-1円となるからです。
1枚の硬貨は{使う,使わない,おつりでもらう}の3通りがあります。
33=27です。
{支払額>おつりの金額}、{0}、{支払額<おつりの金額}の場合があるので、
支払える金額は、(27-1)/2=13通りあります。
1円を支払うのに、1円硬貨を使います。
2円を支払うのに、3円硬貨を使い、おつりを1円もらいます。(3=2+1)
3円を支払うのに、3円硬貨を使います。
4円を支払うのに、3円硬貨と1円硬貨を使います。
5円を支払うのに、9円硬貨を使い、おつりを4円もらいます。(9=5+3+1)
・・・
硬貨の種類を、金額が小さい順に増やすことを考えます。
持っている硬貨を全部使って支払えない最小の金額とそれまでの硬貨の金額を全部足した額の硬貨があればよいことになります。
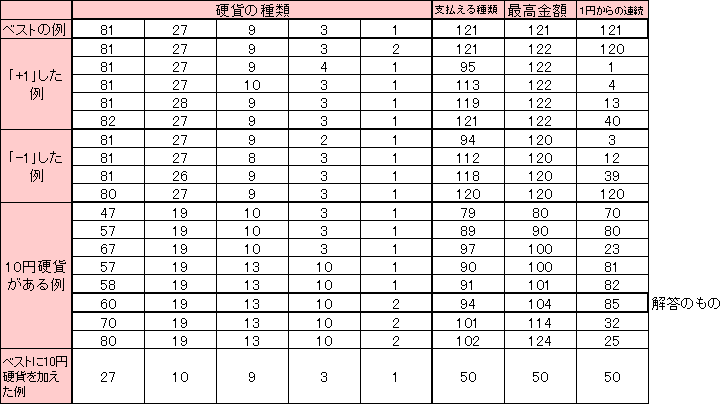
● 5枚の硬貨を使う場合、最大で121通りの支払いが可能です。
10円硬貨が混ざると、上の例からはずれます。
10円硬貨が混ざると、考える糸口として次のことが考えられます。
n円の金額を作れたとき、次のように27通りの金額をつくることができます。
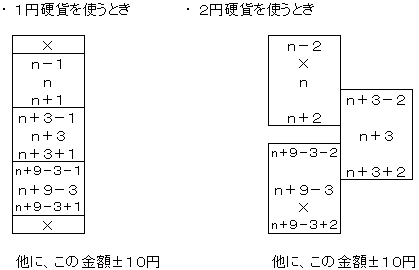
上の×の部分を埋めて、連続した金額をつくるとき、例えば次のような様子になっています。
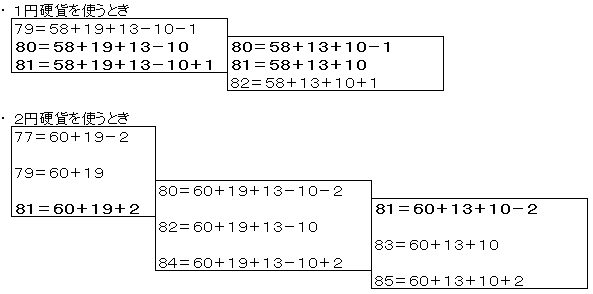
1円硬貨を使う場合、2つ分の金額が重なります。
2円硬貨を使う場合、うまく互い違いになっています。
このように、2円硬貨を使う方が効率が良いように思います。
この差が多分2円硬貨を使う理由の1つでしょう。
このように試行錯誤していくしかないと思います。
以下にいくつかの硬貨の組合せの例を書いておきます。