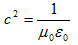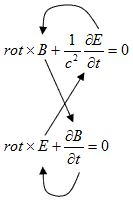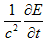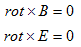NO.1788 重複組合せ(2) 2009.5.5. エルドス
NO.1774 重複組合せを改めて投稿します。
高校数学でもお馴染みの重複組合せの問題に
a1<a2<a3<・・・<am の条件を付け加えると非常に面白い問題になります。
問題1
a1<a2<a3<・・・<am ,
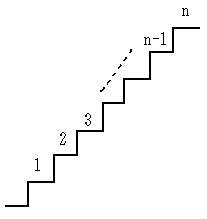
a1+a2+...+am=nを満たすm個の自然数の組合せの数をf(m,n)とするとき、f(m,n)を求めよ。
例1 m=4,n=18のとき、
(1,2,3,12)、(1,2,4,11)、(1,2,5,10)、(1,2,6,9)、(1,2,7,8)、
(1,3,4,10)、(1,3,5,9)、(1,3,6,8)、(1,4,5,8)、(1,4,6,7)
(2,3,4,9)、(2,3,5,8)、(2,3,6,7)、(2,4,5,7)
(3,4,5,6)
よって、f(4,18)=15
【参考1】m=2のとき、関数INT(整数化、切り捨て)を用いて
f(2,n)=INT((n-1)/2)
【参考2】m=3のとき
(1)n=3k+1,3k+2のとき、f(3,n)=( n-1C2 -3*int{(n-1)/2} )/3!
(2)n=3k のとき、f(3,n)=( n-1C2 -3*[(int{(n-1)/2}-1] -1 )/3!
重複組合せ n-1C2 から、同じ数が2個となる場合を引き、
nが3の倍数の時は3個とも同じ数になる場合を引いて3の階乗で割りました。
ただし、この考え方ではmが増えるに従って同じ数になる場合が増えるので、一般化は難しいように思えます。
【参考3】
漸化式を用いて表すと
【1】f(1,1〜n)=1,f(1〜m,0)=0
【2】m≧2のとき、
s=int(m/n),t=n-m*s
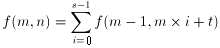
例1のf(4,18)を図に表すと、各過程でのnの減少分を足し合わせると全て18になります。
f(4,18)→f(3,14)→ f(2,11) →f(1, 9)⇒ 4+3+2+1+1+1+1+1+1+1+1+1
(1,*,*,*) (1,2,*,*) (1,2,3,12)
f(1, 7)⇒ 4+3+2+2+1+1+1+1+1+1+1
(1,2,4,11)
f(1, 5)⇒ 4+3+2+2+2+1+1+1+1+1
(1,2,5,10)
f(1,3)⇒ 4+3+2+2+2+2+1+1+1
(1,2,6,9)
f(1, 1)⇒ 4+3+2+2+2+2+2+1
(1,2,7,8)
f(2, 8)→ f(1, 6)⇒ 4+3+3+2+1+1+1+1+1+1
(1,3,*,*) (1,3,4,10)
f(1, 4)⇒ 4+3+3+2+2+1+1+1+1
(1,3,5,9)
f(1, 2)⇒ 4+3+3+2+2+2+1+1
(1,3,6,8)
f(2, 5)→ f(1, 3)⇒ 4+3+3+3+2+1+1+1
(1,4,*,*) (1,4,5,8)
f(1, 1)⇒ 4+3+3+3+2+2+1
(1,4,6,7)
f(3,10)→ f(2, 7)→ f(1, 5)⇒ 4+4+3+2+1+1+1+1+1
(2,*,*,*) (2,3,*,*) (2,3,4,9)
f(1, 3)⇒ 4+4+3+2+2+1+1+1
(2,3,5,8)
f(1, 1)⇒ 4+4+3+2+2+2+1
(2,3,6,7)
f(2, 4)→ f(1, 2)⇒ 4+4+3+3+2+1+1
(2,4,*,*) (2,4,5,7)
f(3, 6)→ f(2, 3)→ f(1, 1)⇒ 4+4+4+3+2+1
(3,*,*,*) (3,4,*,*) (3,4,5,6)
【結論1】f(4,18)は、1,2,3,4を少なくとも1回用いて和が18となる場合の数となっている。
【結論2】用いない数があってもいいと言い換えると、18-(1+2+3+4)=8より、和が8になる場合の数 (8の4までの自然数を用いた分割数)となる。
【結論3】問題2のように0以上の整数にして等号を付けた場合の数をg(m,n)とすると、
f(4,18)=g(4,8)となる。
問題2 0≦a1≦a2≦a3≦・・・≦am ,
a1+a2+...+amを満たすm個の整数の組合せの数をg(m,n)とするとき、g(m,n)を求めよ。
漸化式を用いて表すと
【1】g(1,0〜n)=1,g(1〜m,0)=1
【2】m≧2のとき、
s=int(m/n),t=n-m*s
g(4, 8)→g(3, 8)→ g(2, 8) →g(1, 8)⇒ 1+1+1+1+1+1+1+1
(0,*,*,*) (0,0,*,*) (0,0,0,8)
g(1, 6)⇒ 2+1+1+1+1+1+1
(0,0,1,7)
g(1, 4)⇒ 2+2+1+1+1+1
(0,0,2,6)
g(1, 2)⇒ 2+2+2+1+1
(0,0,3,5)
g(1, 0)⇒ 2+2+2+2
(0,0,4,4)
g(2, 5)→ g(1, 5)⇒ 3+1+1+1+1+1
(0,1,*,*) (0,1,1,6)
g(1, 3)⇒ 3+2+1+1+1
(0,1,2,5)
g(1, 1)⇒ 3+2+2+1
(0,1,3,4)
g(2, 2)→ g(1, 2)⇒ 3+3+1+1
(0,2,*,*) (0,2,2,4)
g(1, 0)⇒ 3+3+2
(0,2,3,3)
g(3, 4)→ g(2, 4)→ g(1, 4)⇒ 4+1+1+1+1
(1,*,*,*) (1,1,*,*) (1,1,1,5)
g(1, 2)⇒ 4+2+1+1
(1,1,2,4)
g(1, 0)⇒ 4+2+2
(1,1,3,3)
g(2, 1)→ g(1, 1)⇒ 4+3+1
(1,2,*,*) (1,2,2,3)
g(3, 0)→ g(2, 0)→ g(1, 0)⇒ 4+4
(2,*,*,*) (2,2,*,*) (2,2,2,2)
以下、f(m,n),g(m,n)を求めるBASICのプログラムです。
同じ漸化式となるので同じループでまとめてみました。
初期値がf(1,1〜n)=1,g(1〜Mmax,0)=1,g(1,0〜Nmax)=1となります。
f(m,n)がs-1まで、g(m,n)がsまでの足しあわせとなっています。
これらも漸化式の図を見ればその意味もよく分かると思います。
Mmax、Nmaxを色々と変えて増減をお楽しみ下さい。
m=nとするとg(m,n)はmの分割数そのものとなります。
また、m≧nのとき、g(m,n)はnの分割数になります。
10 CLEAR 20 OPTION BASE 0 30 INPUT PROMPT "Mmax= ":Mmax 40 INPUT PROMPT "Nmax= ":Nmax 50 DIM f(Mmax,Nmax) 60 DIM g(Mmax,Nmax) 70 REM f(1,1〜n)=1,g(1〜Mmax,0)=1,g(1,0〜Nmax)=1 80 FOR n=1 TO Nmax 90 LET f(1,n)=1 100 NEXT n 110 FOR m=1 TO Mmax 120 LET g(m,0)=1 130 NEXT m 140 FOR n=0 TO Nmax 150 LET g(1,n)=1 160 NEXT n 170 FOR n=1 TO Nmax 180 FOR m=1 TO Mmax 190 LET s=INT(n/m) 200 LET t=n-s*m 210 FOR i=0 TO s-1 220 LET f(m,n)=f(m,n)+f(m-1,m*i+t) 230 NEXT i 240 FOR i=0 TO s 250 LET g(m,n)=g(m,n)+g(m-1,m*i+t) 260 NEXT i 270 NEXT m 280 NEXT n 290 PRINT "f(m,n) a1+a2+a3+...am=n,0<a1<a2<a3<...<am" 300 PRINT "g(m,n) a1+a2+a3+...am=n, a1≦a2≦a3≦...≦am" 310 PRINT "m","n","f(m,n)","g(m,n)" 320 FOR m=2 TO Mmax 330 FOR n=2 TO Nmax 340 PRINT m,n,f(m,n),g(m,n) 350 NEXT n 360 NEXT m 370 END
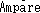 の法則とFaradayの法則を整理した結果、真空中の電磁場の支配方程式、
の法則とFaradayの法則を整理した結果、真空中の電磁場の支配方程式、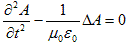 (a)
(a)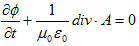 (b)
(b)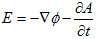 (c)
(c)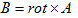 (d)
(d)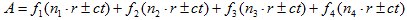 (e)
(e)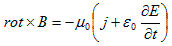 (f)
(f)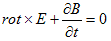 (g)
(g)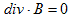 (h)
(h)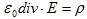 (i)
(i)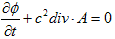 (2)
(2)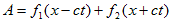 (5)
(5)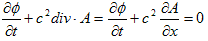 (6)
(6)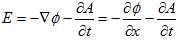 (7)
(7)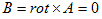 (8)
(8)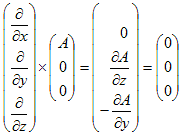
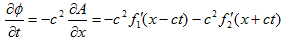 (9)
(9)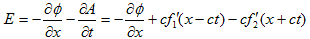 (10)
(10)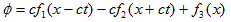 (11)
(11)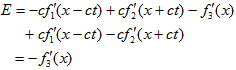
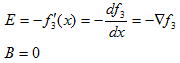 (12)
(12)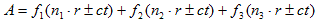 (13)
(13)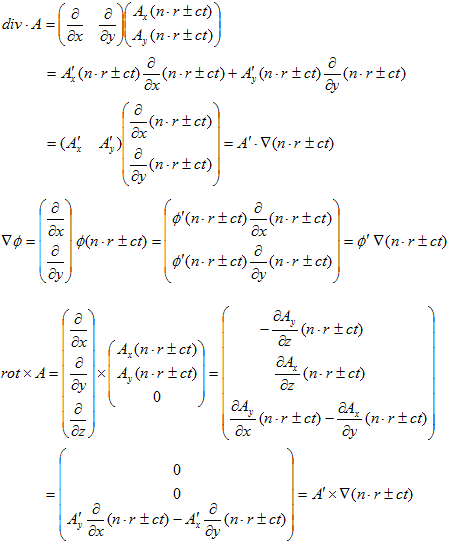
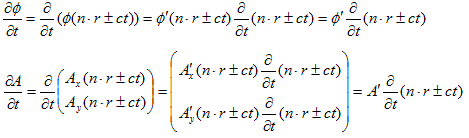
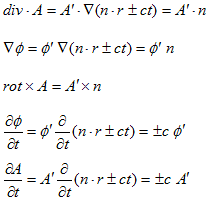
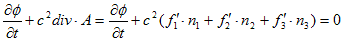 (14)
(14)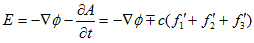 (15)
(15)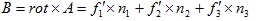 (16)
(16)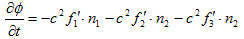
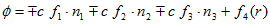 (17)
(17)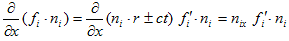
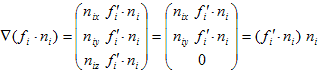
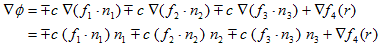 (18)
(18)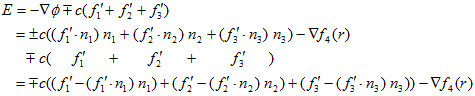
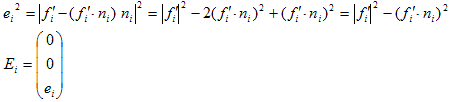
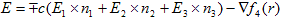 (19)
(19)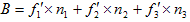
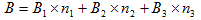 (20)
(20)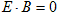 (21)
(21)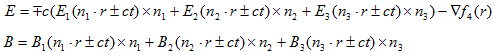
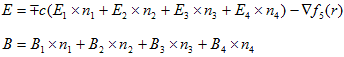 (22)
(22)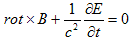 (1)
(1)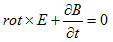 (2)
(2)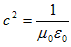 (3)
(3)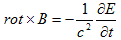 (4)
(4)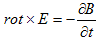 (5)
(5)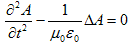 (a)
(a) (b)
(b)