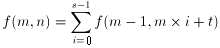NO.1781 多項式の余り 2009.3.23. 水の流れ
第222回数学的な応募問題
先日、「大学への数学」(2009年3月号)を読んでいて、次のような問題を考えました。
問題1:3次関数f(x)=x3−3x2−6x+5について、
(1)f(x)を導関数f’(x)で割った余りを求めよ。
(2)f(x)には極値をとる点が2個あるが、この2点を通る直線の方程式を求めよ。
問題2:f(x)=−x4+4x3+6x2−4xについて
(1)f(x)を導関数f’(x)で割った余りを求めよ。
(2)f(x)には極値をとる点が3個あるが、この3点を通る放物線の方程式を求めよ。
問題3 上の問題1と問題2において、(1)と(2)の答えが同じである理由を考察せよ。
注:この記事に関する投稿の掲載は、2009年4月13日以降とします。
NO.1780 10の倍数(2) 2009.3.23. 夜ふかしのつらいおじさん
問題1
T2は次の表で示すことができます。
左と上の見出しの数をかけたものです。
1から14までの和、105個あります。
15C2でも数えられます。
それらの数を表のように分類します。
後で使うので、右の表のように各行から最後の14行目までそれぞれいくつあるか数えておきます。

解答は右の表の1行目を読んで、T2(2)=77、T2(5)=39、T2(10)=26です。
問題2
T3は次のようになります。
表の左上の黄色の数と左と上の数をかけたもので、太線で囲まれた部分です。
左上の数が1のときは、分類に変化はありません。
黄色の数が1だけ増えると枠が1つ分小さくなります。
T3は1から13までの和、1から12までの和、・・・、1から1までの和の合計の455個あります。
左上の数が1のときは、分類に変化はありません。
左上の数が2のときは、すべてが2の倍数になり、5の倍数であったものは10の倍数になります。

・・・・
以下個数を数えます。

解答は表より
T3(2)=399、T3(5)=235、T3(10)=199
問題3
T4は次のようになります。
表の左上の黄色の2数と左と上の数をかけたもので、太線で囲まれた部分です。

・・・・
以下個数を数えるために、次の場合の個数を調べておきます。

左上の数のそれぞれの場合の個数を数えます。


解答は表より
T4(2)=1295、T4(5)=870、T4(10)=815
NO.1779 藤原先生最終講義 2009.3.15. Junko
昨日、3月14日は、円周率にちなんで「数学の日」ということです。
この「数学の日」に、大学時代にゼミでお世話になった藤原正彦先生の
最終講義を受けてきました。
幼少時代のお話から、アメリカでの経験をお書きになった「若き数学者のアメリカ」の出版、
父親である新田次郎氏との関係、ケンブリッジ大学での様子、
そして数学と文学にも触れられました。
数学の世界では、美的感受性が大切であり、
繊細な自然の中で生きている日本人はこれをもっていると。
改めて、素晴らしい先生にご指導いただけたからこそ、
今の自分があるのだと思いました。
NO.1778 ロシア語の試験問題 2009.3.7. 山崎 昇
サンクトペテルブルクの総合技術大学の入試問題を紹介します。

(青少年物理・数学雑誌「クヴァント」2008年No.2より)
日本語にすると、こんな感じです。
サンクトペテルブルク国立総合技術大学
数学 試験問題
ヴァリアント1(物理・力学学部)
1.次の式を簡単にせよ。
2.次の不等式を解け。
3.与えられた関数のx=1における微分係数を求めよ。
4.長方形の辺の1つが25%だけ増す。面積を前と同じにするには、
他の辺を何%減少させなければならないか。
5.次の不等式を解け。
6.x1、x2が、与えられた方程式の
解をすると、x13x25+x15x23の値はいくらか。
7.与えられた式の値を求めよ。(ctgは、コタンジェント)
8.次の方程式を解け。
9.次の式の値を求めよ。
10.a、bでは、どちらの数が大きいか。
11.次の方程式を解け。
12.はじめの20項の中に33、48、88がある整数項の増加する等差数列の
公差を求めよ。
13.次の式の値を求めよ。(arcsinは、sinの逆関数)
14.次の方程式を解け。
15.次の関数の定義域を求めよ。
16.次の関数の値域を求めよ。
17.次の方程式を解け。
18.直角三角形の直角の頂点から引いた角の二等分線と中線とのなす角のサインは、
1/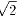 に等しい。二等分線の長さが3のとき、この三角形の面積を求めよ。
に等しい。二等分線の長さが3のとき、この三角形の面積を求めよ。
19.表面積が16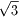 の正四角錐の体積を計算せよ。
の正四角錐の体積を計算せよ。
20.パラメータa>0の値がいくらのとき、次の2つの円は互いに接するか。
NO.1777 ポアンカレ予想解決 2009.3.2. 水の流れ
総合テレビ「NHKスペシャル」で
ポアンカレ予想解決の経緯を綴った「100年の難問はなぜ解けたのか」が,
3月9日 22:00ー22:59に再放送されます。
詳しくは、こちら
前回見逃された方はどうぞご覧ください。
NO.1776 10の倍数 2009.3.2. 水の流れ
第221回数学的な応募問題
先日、生徒から受けた質問から次のような問題を考えました。
今、1から数えて順に15まで自然数がある。ここから重複を許さずn個の数を選び、
それらを全部掛け合わせて得られる数をTnとする。ここで、Tnがkの倍数となる個数
(注:Tnの個数ではなく、選んだ n 個の数の組の個数)を
Tn(k)と表すことにする。例えば、T1(2)=7、T1(3)=5、T1(5)=3
となります。それでは次の質問に答えてください。
問題1:T2(2)、T2(5)、T2(10)の値を求めよ。
問題2:T3(2)、T3(5)、T3(10)の値を求めよ。
問題3:T4(2)、T4(5)、T4(10)の値を求めよ。
注:この記事に関する投稿の掲載は、2009年3月23日以降とします。
NO.1775 行列Aのn乗(2) 2009.3.2. 夜ふかしのつらいおじさん
問題1

問題2
(1)

(2)

問題3
(1)

(2)
問題2の(1)より、α=2、β=3です。
(3)

問題4
(1)

(2)

(3)

(4)

NO.1774 重複組合せ 2009.3.1. エルドス
高校数学でもお馴染みの重複組合せの問題に a1<a2<a3<・・・<am という
条件が一つ加わるだけで思わぬ面白い問題になりました。
試行錯誤していくうちに【参考3】のように漸化式できれいに表せたので、大変喜んでいます。
f(m,n)の一般式を求めるのは可能でしょうか。
問題 a1<a2<a3<・・・<am ,
a1+a2+...+am=nを満たす
m個の自然数の組合せの数をf(m,n)とするとき、f(m,n)の一般式を求めよ。
例1 m=4,n=18のとき、
(1,2,3,12),(1,2,4,11),(1,2,5,10),(1,2,6,9),(1,2,7,8),(1,3,4,10),(1,3,5,9),(1,3,6,8),(1,4,5,8),(1,4,6,7),
(2,3,4,9),(2,3,5,8),(2,3,6,7),(2,4,5,7),
(3,4,5,6)
よって、f(4,18)=15
【参考1】m=2のとき、関数INT(整数化、切り捨て)を用いて
f(2,n)=INT((n-1)/2)
【参考2】m=3のとき
(1)n=3k+1,3k+2のとき、f(3,n)=( n-1C2 -3*int{(n-1)/2} )/3!
(2)n=3k のとき、f(3,n)=( n-1C2 -3*[(int{(n-1)/2}-1] -1 )/3!
重複組合せ n-1C2 から、同じ数が2個となる場合を引き、
さらにnが3の倍数の時は3個とも同じ数になる時を引いて3の階乗で割ると考えました。
ただし、この考え方ではmが増えるに従って同じ数になる場合が増えるので、
一般化は難しいように思えます。
【参考3】
ただし、t=MOD(n,m), s=INT(n/m), n=m*s+t
例2 m=4,n=18のとき、s=4,t=2となり、
f(4,18)=f(3,6)+f(3,10)+f(3,14)=1+4+10=15
f(3, 6)=f(2,3)=1←例1の(3,*,*,*)のとき
f(3,10)=f(2,4)+f(2,7)=1+3=4←例1の(2,*,*,*)のとき
f(3,14)=f(2,5)+f(2,8)+f(2,11)=2+3+5=10←例1の(1,*,*,*)のとき
mについての漸化式できれいに表せるので、もう一息で一般式も導かれるのではと思っています。








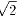 に等しい。二等分線の長さが3のとき、この三角形の面積を求めよ。
に等しい。二等分線の長さが3のとき、この三角形の面積を求めよ。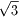 の正四角錐の体積を計算せよ。
の正四角錐の体積を計算せよ。