Weekend Mathematics/コロキウム室/テーマ別/37.ガロア理論の心1
コロキウム室(ガロア理論の心・その1)
| NO.769
| 2000.3.2. | WAHEI | ガロア理論の心(1)
|
(体の代数拡大と指標の独立性)
今回から、ガロア理論を考えてみたいと思います。
これまでの リングセオリーシリーズと
代数方程式シリーズの内容を踏まえれば
この理論を展開する事は、それほど大変な事ではありませんが、
まだ全くやっていない概念もいくつかありまして、
その中で最も基礎的なものは線形代数です。
実はガロア理論は線形代数の知識を使うと意外なほどにすっきりとします。
もともと線形代数は連立方程式論との関係が深いですから、それも当然かもしれません。
それをわかりやすい形で初めて世の中に伝えたのはEmile-Artin先生です。(この人は大先生)
(定義)
Kを体として、kがKの部分体とは、kはKの部分環であってかつk内の0でない元が全て
unitを成す事をいう。この状態をK/kと書いて、Kをkの拡大体という。
上の定義のK/kを「体の拡大」といいます。
最も典型的な体の拡大は複素数体Cと有理数体Qです。
つまりC/Q。
(以下Zと書いたら整数環、Qを有理数体、Rを実数体、Cを複素数体とします。
今まではRと書いたら環を表す事が多かったですが、
これからはAとかBとか書いて環を表します。
この環については断りますが、Z、Q、R、Cについてはいちいち断らない事とします。ご注意)
さて、K/kを体の拡大とします。
k[X]を体k上の多項式環とします。
これは環でしたからこのk[X]を係数とする2変数の多項式環、(k[X])[Y]が作れます。
これをk[X、Y]と書いて2変数の多項式環といいます。
帰納的にn変数の多項式環を次で定義します。
k[X1、X2、・・・、Xn]:=(
k[X1、X2、・・・、Xn-1])[Xn]
ここで代入原理から、Sをkの部分体としますと、Sからkへ内部写像が取れて、
これは環写像ですから、
φ:S[X1、X2、・・・Xn]→kでφ(Xi)=αiなる代入射が取れます。
(但し1≦i≦nで、αiはKの元)この代入射φのイメージ、
つまりIm(φ)をS(α1、α2、・・・αn)と書いて、Sにαiを添加した体といいます。
もう大分昔のことかもしれませんが、
NO.699 代数方程式の代数的解法(1)で書いたことを
数学的に書き直したものです。
与えられた方程式を代数的に解くとは定義体に累乗根を次々と添加していき、
全ての根がその定義体の拡大体に含まれるように拡大の列が取れることでした。
(ベクトル空間について)
今はリングセオリーではないので、ここではよく使われるベクトル空間の定義を書きます。
後で余裕があるようでしたら環を用いてこのベクトル空間を一般化します。
(定義)
アーベル群Vが以下の条件を満たすとき体K上のベクトル空間という。
まず、写像K×V→Vが、(a、m)→amと定まっていて、∀a、b∈K、∀m、n∈Vに対し
- (a+b)m=am+bm
- a(m+n)=am+an
- (ab)m=a(bn)
- 1m=m
群論のレベルではKがVへ左から作用しているということですが、
今はとりあえずそんな事はどうでもよく、
上の定義を満たすVをベクトル空間というのです。
従ってベクトル空間を考えるときは必ず体をベースにして考えなければなりません。
Vの元をベクトルといいます。
高校ではベクトルというと大きさと向きを持つものという感じで定義されていますが、
あれは物理のベクトルであって、今定義したベクトルが数学のベクトルです。
(定義)
n個のベクトルa1、a2・・anがK上一次独立であるとは、
α1a1+α2a2+・・・+αnan=0⇒
α1=α2=・・・=αn=0に限る事をいい、
a1、a2・・・anがK上一次従属であるとは、
少なくとも1つは0でないαiがあって、α1a1+・・・+αnan=0を満たす事をいう。
但しαiはKの元である。
この一次独立や一次従属などは、ベクトル空間の中では最も基本的な言葉です。
(定義)
一次独立なベクトルの最大個数をそのベクトル空間の次元という。
ベクトル空間Vの次元がnであれば、この事をdimV=nと書く。
これもやはり大切な概念です。「体K上」のベクトル空間ということを強調する場合
、Vの次元がnである事を[K:V]=nと書きます。
K/kを体の拡大とすれば、写像k×K→K、(c、x)→cxをうまく定めれば、
Kはk上のベクトル空間になります。
そして、[K:k]でk上ベクトル空間Kの次元を表す事とします。
この次元を拡大次数といいます。
この場合、スカラーは狭いkの方から取ってきていることに注意してください。
(定義)
α∈Kがk上代数的(algebraic)であるとは、
f(α)=0を満たすk[X]の元f(X)が存在する事をいう。但しf(X)≠0とする。
代数方程式の根になる数を代数的といいますが、
これはその概念を一般の体に拡張したものです。
πとかは代数的でない数として有名です(これを証明したのはエルミートという人)。
代数方程式の根になる数というのはよくよく考えてみますと、
コンパスと定規を用いて作図可能な数という事になります。
例えば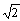 などは1辺が1の正方形の対角線になります。
そうすると、代数的でない数はコンパスと定規を使って作図できない数という事です。
古代から角の3等分線は作図できない事が知られていますし、
与えられた円に等しい面積の正方形の作図もできません。これはπが代数的でないからです。
などは1辺が1の正方形の対角線になります。
そうすると、代数的でない数はコンパスと定規を使って作図できない数という事です。
古代から角の3等分線は作図できない事が知られていますし、
与えられた円に等しい面積の正方形の作図もできません。これはπが代数的でないからです。
α∈Kに対し、写像φ:K[X]→Kをφ(X)=αで定めます。
代入原理からそれは可能でした。
さてこの代入射φのカーネルを考えます。
Ker(φ)=Iとおきます。このときαが代数的⇔I≠{0}です。
なぜなら、αが代数的ならば定義から、f(α)=0なるf(X)≠0がk[X]から取れて、
このことはf(X)∈Iを意味しています。
よってI≠{0}です。逆にI≠{0}を仮定しますと、
0でない元がIの中にあって、それをg(X)とおくと、カーネルの定義から、
φ(g(X))=g(α)=0ですから、αは代数的です。
K[X]はNO.751 リングセオリー(19)の問題13で見たようにPIDでした。
ですからI=(p(X))と書けます。(p(X)∈K[X]です。)
今、p(X)≠0ならばばKが体である事から、その最高次係数をくくりだして、
p(X)の最高次係数が1になるようにできます。
(最高次係数が1の多項式をmonicな多項式といいます)かつp(X)の次数を最小に取ります。
このp(X)をαの最小多項式といいます。
実際、p(X)とは異なるf(X)について、f(α)=0ならば、p(X)|f(X)となります。
このことからも、最小というイメージがつかめると思います。
それから、p(X)|f(X)は整数環の時と同様に、
f(X)=p(X)g(X)なるg(X)が取れることを意味します。
また次数の最小性からp(X)が既約であることもわかります。
従って(p(X))は素イデアルであって、(0)でないから極大イデアルで
(なぜならK[X]も、k[X]もPID)よって、k[X]/Iは体となります。
これは第一同型定理からk(α)と同型です。つまりk[X]/I〜k(α)です。
ここで、k[X]/Iの具体的な形について考えてみましょう。
deg(p(X))=nとおきますと、p(X)はmonicですから、
p(X)=a0+・・・・+Xnと書けます。
∀g(X)∈k[X]を取ってきてp(X)で割ります。
すると、
g(X)=p(X)q(X)+r(X)
但しr(X)=0か、deg(r(X))<deg(p(X))
今p(α)=0を考えれば、g(α)=r(α)ですから、
k[X]/I〜k(α)={a0+・・・an-1αn-1|ai∈k}
となっています。
さらに、1、α、α2、・・・αn-1は一次独立になっています。
(その証明)
a0+a1α+・・・+an-1αn-1=0とすると、
αはg(X)=a0+a1X+・・・+an-1Xn-1の根ですが、
αの最小多項式はp(X)でその次数はnですから、
nより次数が小さい多項式の根とはなりません。
よって、g(X)=0より、a0=・・・=an-1=0となって、
1、α、・・αn-1は一次独立です。
そして、[k(α):k]=nがわかりました。 (証明終わり)
つまり、k(α)/kですが、その拡大次数はαの最小多項式p(X)の次数となっている事が
わかりました。以上の考察からわかった事をまとめてみれば、次の大切なコロラリーを得ます。
(コロラリー)
α∈Kのとき、次は同値である。
- αがk上代数的
- k(α)は体
- [k(α):k]<∞
(3)のことを、体の拡大k(α)/kは有限次拡大であるといいます。
今回はここまでにしまして、次回からは、
具体的な多項式を持ち出して今回やった事を確認しておきましょう。

| NO.771
| 2000.3.5. | WAHEI | ガロア理論の心(2)
|
前回からの続きです。
(定義)
K/kを体の拡大とし、これが代数的(algebraic)であるとは∀α∈Kがk上代数的になっている事
をいう。
さて、ここからが今回の本題です。
(面白そうな方程式)
f(x)=x3−2∈Q[x]とします。
この根はα、αω、αω2の3つであることはわかると思います。
但しαは2の3乗根、ωは1の立方根です。
従ってω2+ω+1=0を満たします。
さて、定義からこの3つの根はQ上代数的でかつ、Q(α、αω、αω2)⊆Cです。
αの最小多項式をp(x)とおきますと前回見たように、
[k(α):k]=deg(p(x))でした。
すなわち拡大次数は最小多項式の次数に等しいのです。
いま、αの最小多項式(もちろんQ上の)はx3−2ですから、
従って[Q(α):Q]=3です。
それから同じようにωのQ上最小多項式はx2+x+1なので[Q(ω):Q]=2です。
ああ、それから、αやωはQの元ではありませんから、
当然Q(α)⊃QとQ(ω)⊃Qが成り立っていますよ。
次に[Q(α、αω、αω2):Q(ω)]と、
[Q(α、αω、αω2):Q(α)]を求めたいのです。
そのためには次の補題が必要でしょう。
(補題1)
Q(α、αω、αω2)=Q(α、ω)が正しい。
(証明)
まず、Q(α、αω、αω2)⊂Q(α、ω)はいえると思います。
といいますのも、α、ω∈Q(α、ω)ですから、
Q(α、ω)が体である事を考えれば、αω、αω2∈Q(α、ω)だからです。
次に逆の包含関係です。
α、αω∈Q(α、αω、αω2)ですから、
やはりQ(α、αω、αω2)が体である事を考えると、
α‐(αω)=ω∈Q(α、αω、αω2)だからです。
よってQ(α、αω、αω2)=Q(α、ω)です。 (証明終わり)
この補題によると、求めたい物は[Q(α、ω):Q(ω)]と、
[Q(α、ω):Q(α)]に化けました。
ところで、2変数多項式の定義はAを環とするとA[x、y]=(A[x])[y]でしたから、
Q(α、ω)=(Q(α))(ω)です。
ですから[Q(α、ω):Q(ω)]を求めるにはQ(ω)上αの最小多項式の次数を
求めれば良いという事になりますね。それをg(x)とおきます。
するとα3−2=0ですから、g(x)|x3−2となります。
よって適当な多項式s(x)を用いてx3−2=g(x)s(x)です。
ところが左辺は既約な多項式ですから、s(x)定数ということになりdeg(g(x))=3
である事がわかります。だから[Q(α、ω):Q(ω)]=3です。
同じように[Q(α、ω):Q(α)]を求めます。
Q(α)上ωの最小多項式をh(x)とします。
するとh(x)|x2+x+1ですから、
x2+x+1=h(x)m(x)と書けます。
左辺は既約ですから、m(x)は定数で、従ってdeg(h(x))=2ですから、
[Q(α、ω):Q(α)]=2となります。
体の拡大次数nの体の拡大K/kを「k→(n)K」で書くことにします。
つまり矢印の行き先が拡大体となっているように書き、
拡大体と矢印の間に拡大次数を書きます。
すると、今考察したことを下のような図に書く事ができます。
Q→(3)Q(α)
↓ ↓
(2) (2)
Q(ω)→(3)Q(α、ω)⊂C
ここまで来ると、次のような疑問が生じます。
つまり上の図で、対角線の拡大次数はどうなっているのかという疑問です。
Q→(n)Q(α、ω)のnをどう求めるかです。
(補題2)
M→(a)N→(b)Kを有限次拡大の体の拡大列とすると、[K:M]=abが正しい。
この補題が言っている事はつまり、[K:N]=b、[N:M]=aでaとbが共に有限ならば、
[K:M]=[K:N][N:M]が成り立つといっています。
それを認めるならば[Q(α、ω):Q]=2・3=6となります。
この補題2の証明ですが、ベクトル空間においての基底の概念をまだはっきりと書いていないので、
それを書いてから証明したいと思います。
(ものすごく簡単な証明ですから、基底や次元についての概念をお持ちの方はやってみてください)
Q(α、ω)=Eとおいて、このEを方程式f(x)=x3−2の分解体といいます。
分解体上では方程式はバラバラに因数分解していることがわかると思います。
またAutE={σ|σ:E→E環同型}とおきますと、
写像の合成を演算に群を成しました
(NO.706 代数方程式の代数的解法(4)を参照)。
このAutEをE上の自己同型群といいます。
ガロア理論の本質はこの自己同型群の部分群と中間体の間に一対一の対応があるという事でした
(NO.706 代数方程式の代数的解法(4)を参照)すなわち、
今の例では、次の集合AとBの間には一対一の対応があります。
A={K|Q⊆K⊆Eなる中間体}
B={H|H<AutE}
但し、H<AutEとは、HはAutEの部分群であることを意味します。
今後この書き方はよく使いますから覚えておいてください。
さて、具体的な対応のつけ方を語る前に言葉を定義します。
Gal(E/K):={σ|σ∈AutEで、∀a∈Kに対してσ(a)=a}
つまりKの元を皆固定するE上自己同型群をこのようにGal(E/K)とかきます。
また、E(H):={x∈E|∀σ∈Hに対しσ(x)=x}として、これをHに対する不変体といいます。
つまりHの元(これは写像)によって動かないEの元です。
また、Gal(E/K)はAutEの部分群となっていて、またE(H)は上のAの元です。
つまり中間体となっています。
(その証明)
まず、恒等写像1は全ての元を固定するE上自己同型ですから、
1∈Gal(E/K)より、Gal(E/K)≠φです。
次に∀τ、σ∈Gal(E/H)を取ってくると、∀a∈Kに対し、τ(a)=a、σ(a)=aで、
従って、a=σ‐(a)です。
よって、τσ‐(a)=τ(σ‐(a))=τ(a)=aより、
τσ‐∈Gal(E/K)ですから、
部分群の定義からGal(E/K)はAutEの部分群です。
従ってGal(E/K)∈B
まや、E(H)が中間体である事を言うので、つまりEの部分体になっている事を言います。
∀σ∈Hに対し、σ(1)=1ですから(なぜならばσは環写像)、
1∈E(H)より、E(H)≠φ。
∀a、b∈E(H)に対し
σ(ab)=σ(a)σ(b)=ab、σ(a+b)=σ(a)+σ(b)=a+b、
σ(-a)=−σ(a)=−aより、ab、a+b、−a∈E(H)で、
さらに、0≠∀a∈E(H)から取ると、Eが体であることからa‐が存在して、
aa‐=1なので、
σ(aa‐)=σ(1)=1⇔σ(a)σ(a‐)=1
よってσ(a)‐=σ(a‐)⇔a‐=σ(a‐)であって、
a‐∈E(H)となり
E(H)はEの部分体ですから、E(H)∈Aです。 (証明終わり)
このことから、集合AとBの間には次のような対応がついていることがわかりました。
B∋H→E(H)∈A
A∋K→Gal(E/K)∈B
今は方程式x3−2について考えています。
それから、Gal(E/K)を方程式x3−2の分解体EにおけるK上ガロア群といいます。
代数方程式が代数的に解けるためには、
このガロア群が可解である事が必要かつ十分であることが証明されます。
ここで実際にガロア群の計算に入りましょう。
(例1)
m∈Qとし、√mを無理数とします。
ここでf(x)=x2−mのQ上ガロア群を求めてみたいと思います。
まずこの方程式の分解体EはもちろんQ(√m)です。
求めるべきはGal(E/Q)=Gal(Q(√m)/Q)ですね。
ここから少し受験っぽいテクニックを使います。
∀φ∈Gal(E/Q)に対して、今考えなければならない事は無理数である√mがどう移るかです。
といいますのもQ上の環写像はすべて恒等写像ですから
(NO.751 リングセオリー(19)の問題を参照)。
ここで、0=φ(0)=φ((√m)2−m)=φ(√m)2−φ(m)ですから
(ここが受験時代に培ったセンスの発揮所です)、
φ(m)=mを考えて(なぜなら、くどいですが、Q上の環写像は恒等写像なので)
m=φ(√m)2です。
従ってφ(√m)=±√mである事がわかります。
f(x)=0なる方程式の根はもちろん±√mですから、φ(√m)はf(x)の根です。
ここがポイントです。
つまりここから方程式上のガロア群はその方程式の根の置換を引き起こす事が予想されるのです
(それが正しいことをすぐに証明します)。
さて、分解体E=Q(√m)の任意の元はa+b√mという形をしているので(なぜならQ(√m)
は多項式環Q[x]に√mを代入したのもだから)、
a、b∈Qを考えてφ(a+b√m)=φ(a)+φ(b)φ(√m)=a±b√mです。
よってφ(√m)=√mならばφは恒等写像1です。
またφ(√m)=−√mならば、φはEの元をa−b√mに移す事がわかりました。
従ってGal(E/Q)=Gal(Q(√m)/Q)={1、φ}である事がわかります。
但しφはφ(a+b√m)=a−b√mなる環同型です。
この場合は方程式f(x)=0上のガロア群は位数2の群であることがわかりました。
(方程式上のガロア群の元はその方程式の根を置換する写像となっている事の証明)
Kを体としEをf(x)∈K[x]の分解体とする。
Gal(E/K)∋∀φに対して、f(x)=a0+a1x+・・・anxnとする。
φはKの元を固定するE上の自己同型なのでこの場合、
f(x)の係数を全て固定するので、
φ(f(x))=a0+a1φ(x)+・・・+anφ(x)nだが、
f(x)の根をαとすると、
f(α)=0なのでφ(f(α))=a0+a1φ(α)+・・・+anφ(α)n=0。
従ってαがf(x)の根ならばφ(α)もf(x)の根である。 (証明終わり)
このことは簡単な事ですが、極めて重要な事です。
(例2)
f(x)=x2+1を考えて、この方程式のQ上のガロア群を今度は求めてみましょう。
この方程式の分解体はQ(i)で、従って求めるべきはGal(Q(i)/Q)です。
Q上の環写像は全て恒等写像です(できる限りこれを確かめて下さい。但し少し高級です)。
ですから例1と同じようにして、Gal(C/R)={1、φ}です。
但しφ(a+bi)=a−biです。
このガロア群ではf(x)=0の根±iで、
i→−iと−i→iと根を置換していることに注意してください。
今回はこれくらいにして、次回からいよいよ前半の山である、
「指標の独立性」を考えて見ましょう。
ところで、ぜひ皆さんも適当な方程式を作って定義体
(NO.699 代数方程式の代数的解法(1)参照)に根を添加して図などを書いて「遊んで」みてください。
世界が広がる事を保証いたします。

| NO.779
| 2000.3.12. | WAHEI | ガロア理論の心(3)
|
(群指標とその独立性)
ここではガロアの基本定理を解く鍵となる、指標の独立性を考えます。
そこで群の準同型写像を定めましょう。といっても別に新しい事ではありませんが…
(定義)
AとBを積で群とする。
写像f:A→Bが群の準同型写像であるとは、f(ab)=f(a)f(b)を満たす事を言う。
従ってeをAの単位元、e´をBの単位元とするなら、f(e)=e´が成り立つ。
一般に演算を保つものを準同型写像と言いました。
ですから、環写像はもちろん準同型写像です。
ここで、体は積でアーベル群を成していましたから、
群Gと体kの間に矛盾なく群の準同型写像を定められるはずです。
この群から体に向かう群の準同型写像を体kにおける群Gの指標といいます。
定義を厳密に書くと次のようになるでしょう。
(定義)
G´={σ|σ:G→kで群の準同型写像}として、
∀α∈Gに対しσ(α)≠0を仮定する。このσを体kにおける群Gの指標という。
今は演算は積としていますから、σ(α)=0では意味を成さない事に注意してください。
さて、次に書くのが有名な指標の独立性です。
(定理)…指標の独立性
σ1……σn∈G´を相異なる群指標とする。
(つまり写像として異なっている)このとき
α1σ1(x)+…+αnσn(x)=0
(∀αi∈k、∀x∈G)ならば、α1=…=αn=0が正しい
(但し1≦i≦n)
つまり指標によって移されたGの元は体k上で1次独立になっているということです。
この証明はArtin先生のうまい方法に従いましょう。
(Artin先生の証明)
nに対する帰納法で示す。
n=1の時はα1σ1(x)=0で、
σ1(x)≠0であり、
体は全て整域なのでα1=0であるから成り立つ。
だからn>1として、n−1まで定理の主張が正しいとする。
今yをGから任意にとってxとの積yxを考えると群は演算が備わっているので
当然このyxもGの任意の元である。
そこで、xをyxに置き換える。すると、
α1σ1(yx)+…+αnσn(yx)=0
であって、今σ達は群の準同型なので、
α1σ1(y)σ1(x)+…+αnσn(y)σn(x)=0となる。この式を(1)とおく。
さて、ここで元の式、つまり
α1σ1(x)+…+αnσn(x)=0の両辺にσn(y)をかける。
すると、
α1σn(y)σ1(x)+…+αnσn(y)σn(x)=0
となり(なぜならσは準同型写像なので)この式を(2)とおく。
さて、ここで(1)−(2)を実行する。すると、n番目の項が打ち消される。
α1σ1(x)(σ1(y)−σn(y))+…+αn−1σn−1(x)
(σn−1(y)−σn(y))=0
従って帰納法の仮定により特にα1(σ1(y)−σn(y))=0としてよい。
今はn>1なので、
σ1(y)とσn(y)は等しくないから、
α1=0である。
よって以下同じようにα2=α3=…=αn−1=0なので、αn=0
となる。 (証明終わり)
どうでしょうか?いつ考えてみても非の打ち所のない完璧な証明です。
この指標の独立性のコロラリーとして、次の補題を得ます。
(補題1)
体KとLに対してσ1、σ2、…、σn:K→Lを相異なる環写像とすると、
α1σ1(x)+…+αnσn(x)=0ならば、
α1=α2=…=αn=0である。
(但し∀αi∈K、∀x∈Gで1≦i≦n)
この補題はDedekind(デデキント)の補題と言われています。
(スペリングは自信ありません)証明はもう済んでいます。なぜなら環写像は群の準同型となるからです。
さて、僕自身も大分忘れかけていますから、復習をしながら進んでいきましょう。
方程式上の分解体をEとし、その自己同型群AutEを考えます。
GをAutEの部分群とし、E(G)はGの元(写像)で動かないEの元の集合で、
Gに対する不変体と言いました。
またこのE(G)はEの部分体になっている事はすぐにわかります。
ですから、体の拡大E/E(G)を得ます。ではこの拡大次数はどうなっているでしょうか?
つまり、[E:E(G)]を求めたいのです。
(補題2)
G={σ1、σ2、…σn}とおく。すると、[E:E(G)]≧nが正しい。
この補題がいっている事を整理してみますと、AutEの部分群Gが上のようにn個の元から成っていれば、
体の拡大E/E(G)の拡大次数は少なくともnよりは大きい、
つまり、|G|より大きいと言っています。本当でしょうか?
(補題の証明)
背理法で示す。すなわち[E:E(G)]=r<nとして矛盾を導く。
[E:E(G)]=rで、これはE(G)上のベクトル空間Eの次元を表していて、
次元とは一次独立なベクトルの最大個数であった。
これらのベクトルをベクトル空間Eの基底という。
従って基底の個数とベクトル空間の次元は一致する。
さて、Eの基底は今r個あるのでその基底を1組持ってくることができ
(基底の取り方は一意的ではありません。よく知る2次元の平面で考えるとわかります)、
それらを{ω1、ω2、…ωr}とする。(基底はこのように集合の形で書く)
ここで次の連立方程式を考える。
σ1(ω1)x1+σ2(ω1)x2+…+σn(ω1)xn=0
……………
σ1(ωr)x1+σ2(ωr)x2+…+σn(ωr)xn=0
この連立方程式は未知数、つまりxの個数がn個で方程式の個数がr個、
従ってr<nを考えればこの連立方程式は非自明な解を持つ(これについてはこの証明が終わってから解説します)。
(x1、x2、…xn)≠0とする。
∀α∈Eは基底の線形和として一意的に書けるので(これについても後でやります)、
α=a1ω1+…+arωrと書ける。
(ai∈E(G)で1≦i≦r)
第j番目の方程式にσ1(ωj)を掛けると、次のようになる。(1≦j≦r)
σ1(a1ω1)x1+…+σn(a1ω1)xn=0
………
σ1(arωr)x1+…+σn(arωr)xn=0
これらの式を一斉に加え、
かつα=a1ω1+…+arωrを考え
次の式を得る。
σ1(α)x1+…+σn(α)xn=0
ところが、元の方程式が非自明な解をもつので、x1、x2、…xnのどれかは0でない。
これは指標の独立性に矛盾する。よって、[E:E(G)]≧nである。 (証明終わり)
さて、ガロア理論の本質というのは分解体上の自己同型群の部分群と分解体以下の中間体との間に
一対一対応があるということでした。
実はこれはどんな体拡大に関してもいえるわけではありません。
今まで取り上げた例は全てある特殊な拡大になっていたのです。
(定義)…ガロア拡大
K/Fを体の拡大とする。
この拡大がガロアである(またはガロア拡大である)とは、F=K(G)となるAutKの部分群Gが取れることを言う。
今まで考えてきた事によるとAutKの部分群としてGal(K/F)が取れていたわけです。
さらに上で示した補題2を芸術にまで昇華した定理として次を挙げる事ができます。
(ガロアの定理)
補題2と同じ仮定でGが有限群ならば、[E:E(G)]=|G|が成り立つ。
(証明)
補題2より、[E:E(G)]≧n=|G|は言えている。
示すべきは[E:E(G)]≦nである。
これを示すにはα1、α2、…αn−1∈Eが常に一次従属である事を言えばいい。
G={σ1、σ2、…σn}とする。
ここで補題2と同じ方針で非自明解をもつ連立方程式を作ることを考える。
そこでつぎの方程式を考えるとうまくいく。
σ1−(α1)x1+…+σ1−(αn+1)xn+1=0
………
σn−(α1)x1+…+σn−(αn+1)xn+1=0
これは未知数の個数がn+1個であり、方程式の個数がn個であるので非自明解を持つ
(後で証明します。今はとりあえず読み飛ばしてください)。
従って特にx1≠0としてよい。この連立方程式の第i番目の式にσiを施すと
σi(σi−(α1)x1+…+σi−(αn+1)xn+1)=0
となり、iに対して和を取る。すると、
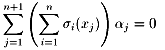 となる。
となる。
ここでx1≠0より、σ1(x1)≠0であって、
よってこれはα1、α2、…αn+1が一次従属である事を示している。
従って[E:E(G)]=|G|を得る。
(証明終わり)
この等式、つまりGが有限群ならば、[E:E(G)]=|G|は有名なオイラーの公式と同等に美しい公式として知られ、
大学の学部のレベルで理解できる数学としては最も綺麗な公式とされています。
このガロアの定理のコロラリーとして、次を得ます。
(コロラリー)
Gal(E/E(G))=G
この等式も実に綺麗です。全く感動物ですね!
(補題)
G1、G2<AutEを2つとも有限部分群とする。
このときG1=G2⇔E(G1)=E(G2)
(証明)
まず⇒は全く自明。問題は逆方向です。
G1=Gal(E/E(G1))=Gal(E/E(G2))=G2
従ってG1=G2を得ます。これはすぐ上のコロラリーを使えば割りと簡単ですね。 (証明終わり)
これによるとガロアの理論(すなわち分解体上自己同型群の部分群と中間体の間に一対一対応が存在)において、
AutEの部分群Gは拡大E/Fに対して唯1つ定まり、
G=Gal(E/F)であると言っています。
それでは、いよいよガロアの基本定理を料理しましょう。
(ガロアの基本定理の前半…Fundamental Galois Theorem Stage 1)
K/Fを有限次のガロア拡大とする。
このときK/Fの中間体の集合AとG=Gal(K/F)の部分群の集合Bの間には
次のような一対一対応がつく。
m:A→B
n:B→A
でn(m(A))=A(つまり写像nとmの合成がA上の恒等写像)かつ、
m(n(B))=B(つまり写像mとnの合成がB上の恒等写像)
ガロアの基本定理というのはこの前半と後半を合わせた物ですが、
後半の証明は次回に回して(申し訳ありませんがベクトル空間の基本概念も次回に回します)、
今回はこの前半の証明をやって終わりましょう。
(前半の証明)
m(n(B))=Bはつまり、∀G∈Bに対してmn(G)=GということなのでGal(K/K(G))=Gであって、
ガロアの定理とそのコロラリーから成立している。(うまい対応がすでについていましたね)
n(m(A))=Aが問題である。
これは∀E∈Aに対してnm(E)=Eということなので、K(Gal(K/E))=Eを示せばいい
(なぜならば、不変体というのは分解体の中間体でしたから)。
ここでK(Gal(K/E))⊇Eは明らかである
(不変体とガロア群の定義からこれは明らかとしていいと思うのです。
でも腑に落ちない方はきちんと納得がいくまで考えてください)。
従ってK(Gal(K/E))⊆Eを示せばいい。
便宜上、H=Gal(K/E)とおき、またE´=K(H)とおく。
ガロアの定理とそのコロラリーからK/K(H)は有限次ガロア拡大であって、
従って[K:K(H)]=|H|が成り立つ。
ここで体の拡大次数の関係式[K:F]=[K:E´][E´:F]
(これはNO.771 ガロア理論の心(2)で書いたと思うのですが、その証明はまだやっていませんでした。
次回にやりたいと思います)と、
群の指数と位数の関係式
|G|=|H|[G:H]
(これは代数方程式シリーズでやりました。
ここで紛らわしくて恐縮ですが[G:H]は体の拡大次数ではなく、
群GのHに関する指数です)
はガロアの理論によると対応しているから
(ここが本質的です。すなわち体の拡大次数と群の指数は対応しているのです)、次を得る。
[E´:F]=[K:F]/[K:E´]=|G|/|H|=[G:H]
従って[E´:F]=[G:H]=rとおいてGを同値類に分解する。
(この話は全て代数方程式シリーズに書いてあります。忘れた方はもう一度見直してみてください)
G=a1H∪a2H∪…∪arH
ここでaiは全てGの元であって、よって写像である事に注意する。
(1≦i≦r)このai達をE上へ制限する。
但し、写像の制限とは、写像f:A→Bがあって、CをAの部分集合とすれば、
f|C;C→Bとして、写像fをCへ制限するという。
すなわちAの部分集合Cの元をfでBへ移す事をいう。
さて、a1|E、a2|E、…ar|E :E→K相異なる。
なぜならば、ai(α)=aj(α)が∀Eについて成り立つなら、
aj−aiはEの元を固定するK上自己同型なので、
aj−ai∈Hとなって
これはG上の同値関係R11となっている
(代数方程式シリーズ参照)ので、
ajとaiは同じ同値類に属している(分割の補題より)から、
i=jとなる。従ってガロアの定理から
[E:F]≧r=[E´:F]であるからE=E´がわかる。 (証明終わり)
正直にいうと、今回の内容はかなり高度です。
さすがにガロアの理論と言われるだけあるでしょう。
もちろん一回読んだだけでは意味がさっぱりわからないと思っております。
何回も自分がわかるまで読んでみるといいでしょう。
ですから何も僕のやり方でなくともいいわけです。
ベクトル空間の内容はともかくとして、それ以外は全て今まででやってきた事ですから、
わからなくとも悲観する事をせずに、
特に代数方程式シリーズを読み直してみるといいでしょう。
次回にこのガロアの基本定理の後半を示して、ベクトル空間の基本性質を簡単に紹介して可解群に入りたいと思っております。

 戻る
戻る
 次へ
次へ
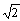 などは1辺が1の正方形の対角線になります。
そうすると、代数的でない数はコンパスと定規を使って作図できない数という事です。
古代から角の3等分線は作図できない事が知られていますし、
与えられた円に等しい面積の正方形の作図もできません。これはπが代数的でないからです。
などは1辺が1の正方形の対角線になります。
そうすると、代数的でない数はコンパスと定規を使って作図できない数という事です。
古代から角の3等分線は作図できない事が知られていますし、
与えられた円に等しい面積の正方形の作図もできません。これはπが代数的でないからです。
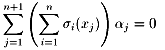 となる。
となる。 戻る
戻る
 次へ
次へ