NO.796�@�o�Ȑ����i�R�j�̃O���t����킩��悤�ɁA ��`����w���O�Ƃ����O�ɕ����čl���Ȃ���Ȃ�܂���B
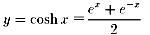 �@��ό`���邱�Ƃɂ��A
�@��ό`���邱�Ƃɂ��A(����)�Q�|�Q�������{�P���O
���������Ƃ��邱�Ƃɂ��A���Q�|�Q�����{�P���O
Weekend Mathematics�^�R���L�E�����^2000.4�`6�^NO.93
| NO.797 | 2000.4.6. | Junko | �o�Ȑ��� �i�S�j |
���āAy=cosh x �̋t�����l���܂��B
NO.796�@�o�Ȑ����i�R�j�̃O���t����킩��悤�ɁA
��`����w���O�Ƃ����O�ɕ����čl���Ȃ���Ȃ�܂���B
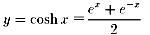 �@��ό`���邱�Ƃɂ��A
�@��ό`���邱�Ƃɂ��A
(����)�Q�|�Q�������{�P���O
���������Ƃ��邱�Ƃɂ��A���Q�|�Q�����{�P���O
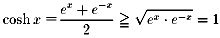
���̌������A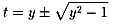
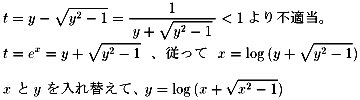
�@
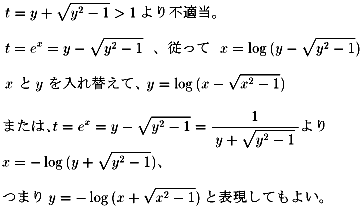
�@

| NO.798 | 2000.4.8. | WAHEI | �K���A���_�̐S�i�T�j |
�i���Q�Ƃr�i���j�̕s�𐫁j
�܂��͎��̕�肩�炢���܂��B
�i���P�j
�g�A�j���Q�f�ɕ����Q�Ƃ��A�g�j���o�����b�����g�A�����j�p�Ƃ����B
���̂Ƃ����̂g�j���f�ɕ����Q�ł��邽�߂̕K�v���\�������͂g�j���j�g�ƂȂ邱�Ƃł���B
�i�ؖ��j
�g�j���f�̕����Q�ł���Ɖ��肷��B
���̂Ƃ��������g�j�ɂ������āi�����j�]�����]���]���g�j�ł��邩��A
���邈�P���g�A���P���j�����݂��āA
���]���]�����P���P���i�����j�]�Ƃ�����B
�]���Ă��������P�]���P�]���j�g�ł���B
�܂�g�j���j�g���������B
�܂��i�����j�]�����]���]�Ȃ̂Łi�����j�]���g�j�A
����Ă������g�j�ƂȂ�A�j�g���g�j�ƂȂ��āA�j�g���j�g�B
����g�j���j�g�����肷��B
����Ɓi�����j�i���P���P�j�]���������P�]���P�]
�����i�����P�]���P�]�j�ŁA
�����P�]���P�]���j�g���g�j�Ȃ̂ŁA
�����P�]���P�]�����Q���Q�Ƃ�����
�i���Q���g�A���Q���j�j�B
�����炈�i�����P�]���P�]�j�����i���Q���Q�j���g�j�ƂȂ���
�g�j�͊m���ɂf�̕����Q�B
�@�@�@�i�ؖ��I���j
�i�R�������[�P�j
�m�A�g�͂f�̕����Q�Ƃ���B
�����m���f�̐��K�����Q�Ȃ�A�W���m�g�͕K���f�̕����Q�B
�i�ؖ��j
��̕��Ɛ��K�����Q�̒�`�ɏ]���B�@�@�@�@�i�ؖ��I���j
���āA���̒藝�͌Q�̑�^�藝�ƌĂ����̂ł��B
�i�藝�P�j
�m�A�g�͂f�̕����Q�łm�͂f�̐��K�����Q�ł���Ɖ��肷��B
�m���g�͂g�̐��K�����Q�łm�͂m�g�̐��K�����Q�ł����āA�������g�^�m���g�`�m�g�^�m�ł���B
�i�ؖ��j
�m���m�g�̐��K�����Q�ł��邱�Ƃ͑S�������B
�Q�̏����^�ʑ����F�g���m�g�^�m�����i���j�����m�Œ�߂�Ƃ����킩��悤��
�j�����i���j���m���m�Ȃ̂őO�����悤�ɂ���͂g�̐��K�����Q�ł���B
��������m�A�����g�Ƃ���ƁA�i�����j�m���i�����j�m�����m��肆�͑S�˂ł���B
�����NO.791 �K���A���_�̐S�i�S�j
�̃R�������[�Q����A�g�^�m���g�`�m�g�^�m��������B
�@�@�@�@�i�ؖ��I���j
���āA�������炪����̖{��ł��B���Q���`���܂��傤�B
�i��`�P�j
�f���Q�Ƃ���B
���̂f�����ł���Ƃ͂f���̕����Q�̗�A�f���f�P���f�Q���c���f�����o���p�ɂ����āA
�f�k�{�P�͂f�k�̐��K�����Q�ł��A
�f�k�{�P�^�f�k���A�[�x���Q�ƂȂ邱�Ƃ������B
���̒�`���炷�ׂẴA�[�x���Q�͉��ł��邱�Ƃ��킩��܂��B���̕��Q����{�I�ł��B
�i���Q�j
(�ؖ�)
�f�����Ƃ���Ƃf�̕����Q�̗�f���f�P���f�Q���c���f�����o���p��
��̒�`�������̂�����B
�����łg���f�̕����Q�Ƃ��A�g���f�����g���i�P���������j�Ƃ����
�g���g�P���g�Q���c���g�����o���p�ƂȂ��ĉ��̒�`���݂����B
�]���Ăf�̕����Q�g�͂f�����Ȃ�Ή��ł���B
�܂��f�L�������i�f���j�Ƃ����Ƃf�L���ɕ����Q�̗��ĉ��̒�`�������Ƃ�
��^�藝����킩��B
����Łi�P�j���������B
���Ɂi�Q�j�������B
�f�L���f�^�m�Ƃ����A���F�f���f�L�����R�Ȏʑ��Ƃ���B
�܂��f�L���ʼn��̒�`�����悤�ɕ����Q�̗�f�L���i�P���������j�����邪�A
�f�������]�i�f�L���j�Ƃ�����
�f�̕����Q�̗�f���͉��̒�`�����A����ɂf�����m�ł���B
�m�����Ȃ̂łm�̕����Q�̗�m���i�P���������j�Œ�`�����悤�Ɏ���
�]���Ăf���g���ł���B�@�@�@�i�ؖ������j
�����Ńt�@�N�^�[�O���[�v���A�[�x���Q�ɂȂ�������l���܂��傤�B
���A�����f�̌��Ƃ���
�m���A���n�F���������]���]�Ƃ��A��������Ƃ��̌����q�Ƃ����܂��B
�f�̗L���̌����q�̐ς̑S�̂��m�f�A�f�n�Ə����܂��Ƃ���͂f�̕����Q�ƂȂ�
�i�ؖ��͊ȒP�Ȃ̂ŊF����ɔC�����ق��������ł��傤�j�f�̌����q�Q�Ƃ����܂��B
�i�藝�Q�j
�g���f�̕����Q�Ƃ���B
�g���f�̐��K�����Q�ł��f�^�g���A�[�x���Q�ł��邽�߂̕K�v���\�������͂g���f�̌����q�Q�A
�m�f�A�f�n���܂ނ��Ƃł���B
���Ɍ����q�Q�m�f�C�f�n�͐��K�����Q�ł���B
�i�ؖ��j
�g���f�̐��K�����Q�ŁA�f�^�g���A�[�x���Q�ł���Ɖ��肷��B
���f�^�g�̔C�ӂ̂Q���`�����g�A�a�����g�����B
�f�^�g���A�[�x���Q�ł��鎖����`�a�`�]�a�]���g�ł���B
�]���Ă������]���]�g���g�Ȃ̂ł���͂������]���]���g�������B
����ām�f�A�f�n���g�ł���B
�t�ɂg���f�̕����Q�Ƃ��āA�g���m�f�A�f�n�����肷��B
�����g�A�����f�ɑ��Ă������]���������]���]�����m���A���n����
�m�f�A�f�n�����g�����g��
���邩��g�͐��K�����Q�ł���B
�����������i���]���]�����j�������m���]�A���]�n�ŁA
�m���]�A���]�n���m�f�A�f�n���g�ł��邩��
�����g�������m���]�A���]�n�g�������g�B
�]���Ă`�����g�A�a�����g�Ƃ����Ƃ`�a�����g���g�������g�������g�����g���g���a�`�ƂȂ���
�f�^�g�̓A�[�x���Q�ł���B�@�@�@�@�@�i�ؖ��I���j
��ʂɂ������̕�����בւ���̂͂Q���̕��ёւ������J��Ԃ��čs�������킯�ł��B
���̂�����܂��̎����𐔊w�I�ɍl�@���܂��傤�B
�R���Ώ̌Q�r�i�R�j�̒��ɂ͎��̂悤�ȁA�����ʂȌ�������܂��B
����́i�P���Q�A�Q���R�A�R���P�j�ł��B������R�̏���u���Ƃ����܂�
����Ē������̏���u���Ƃ����̂͂P���Q�ɂQ���R�Ɂc���|�P�����ɂ����P�ɒu��������̂�
���Ώ̌Q�ɂ͕K���܂܂�Ă��鎖���킩��ł��傤�B
�܂������Q�̏���u�����݊��Ƃ����܂��B����đS�Ă̒u���͌݊��̐ςƂ��ď������ł��B
�i���R�j
�����T�Ƃ��f�͂r�i���j�̕����Q�Ƃ���B
�m�͂f�̐��K�����Q�łf�^�m�̓A�[�x���Q�ł���Ɖ��肹��B
���̂Ƃ��f�������R�̏���u����S�Ċ܂ނȂ�m�������R�̏���u����S�Ċ܂ށB
�i�ؖ��j
���F�f���f�^�m�����R�Ȏʑ��Ƃ���B
�����P������������������C�ӂɎ��A����ɂ��A���A���Ƃ͈قȂ�Q�������A���i�A���������j��
�P���炎�͈̔͂Ŏ���ď���u�������i�������A�������A�������j��
�����i�������A�������A�������j�Ƃ��l����B
�f�^�m�̓A�[�x���Q�Ȃ̂Œ藝�Q���炆�i���j�]���i���j�]���i���j���i���j�����ł���
�i���͂������P�ʌ��j�B
�]���āi�������A�������A�������j�����]���]������
���̃J�[�l���ł���m�Ɋ܂܂��B
�i�ؖ��I���j
���̒藝�͂T���ȏ�̑㐔�������ɂ͍��̌������Ȃ��Ƃ����A�[�x���̒藝�Ƌɂ߂Ė��ڂɊW���Ă��܂��B
�i���c�A�[�x���j
�����T�Ȃ�r�i���j�͉��łȂ��B
�i�ؖ��j
�����T�ȏ�ł������r�i���j�͉��ł���Ɖ��肹��B
�f���r�i���j�Ƃ����f�̕����Q�̗�f�������̒�`�����悤�Ɏ��B
����ƕ��R��p����Ə��Ԃɂf���f�P�A�f�Q�c�f���͒����R�̏���u����S�Ċ܂ނ��ƂɂȂ邪
�Ō�̂f���́o���p�ł��邩�炱��͕s�\�ł���B�@�@�i�ؖ��I���j
�i�K���A���_����肽���������R�j
�悤�₭�K���A���_�̐S��������x���������ł��܂����B
�u�K���A���_�Ƃ́H�v�ƕ����Ƃ����܂��
�u�����A����Ȃ�T���ȏ�̕������������Ȃ����Ď��ł��傤�v�Ƃ����Ԏ����܂����A
����͑�ςȌ���ł��B
�K���A���_�̐^���͑O�ɂ��������ʂ�ł�����A
�����ǂ��̓L�`���Ɠ����鎖���ł���ł��傤�B
���Ėl�͐�傪���_�i���������������������� ���������������j�Ȃ̂ŃK���A���_�Ƃ̊W��
����قNj����Ƃ͂����܂��A
�㐔�w���w�ƌ����邽�߂ɂ̓K���A���_���w��ł��Ȃ���Ȃ�܂���B
�]���Ă��̃K���A���_�Ƃ����̂͑㐔�w�̑㖼���̂悤�Ȃ��̂ł��B
�ł����瓖�R�Ȃ܂₳�������ł͂���܂���B
�l���K���A���_����肽�������̂́A���͂��̂悤�Ȏ���������̂ł��B
�i�{�̏Љ�j
�����ŏ����{���Љ�܂��B
�i�㐔�\���Ɋւ���{�j
M.F.Atiyah�@and�@I.G.Macdonald�@�gIntroduction to Commutative Algebra�h
D.A.R.Wallace�@�gGroups,Rings and Fields�h
P.M.Cohn�@�gAn Introduction to Ring Theory�h
�ȏ�ɋ������{�͂�������D�ꂽ�{���Ǝv���܂��B
�l���g�����ԑ������w�т܂����B
�����O�Z�I���[�V���[�Y�͑�̂����̖{�̓��e�Ɠ����ł��B
�hIntroduction to Commutative Algebra�h�͍��ł͓���͍���ƂȂ��Ă��܂����A
��w�̐��w�Ȃ̐}���قɍs������Ǝv���܂��B
�܂����w�Ȃ͂ǂ��������̕����e�ł�����A�s���Ή�������Ή����Ă����͂��ł��B
�gGroups,Rings and Fiels�g��Springer����o�ł���Ă��āA
��r�I�V�����{�ł�����e�ՂɎ�ɓ������Ǝv���܂��B
���̖{�͑㐔�\���Ƃ�����Q�A�A�̂����ؒ��J�ɓW�J����D���ł��B
�l���W�J�������̂Ƃ͂܂��ꖡ������W�J�̎d���œǂ�ł��Ėʔ����ł��B
�gAn Introduction to Ring Theory�g�͕����ǂ���u�����O�Z�I���[�v�̓��发�ł��B
���Z�����ǂނ̂͂����Ǝv���܂����A��w�̐��w�Ȃ̂Q�N�����x�̒m��������Γǂ߂�Ǝv���܂��B
���̖{��Springer���o���Ă��܂��B
�i�K���A���_�Ɋւ���{�j
�Ȃ�ƌ����Ă����̖{����Ԃł��B
Emile Artin�@�gGALOISSE THEORIE�h
���͂��̖{�͓��{��ł��o�ł���Ă��܂��B���̖����u�K���A���_����v�ł��B
�o�ł��Ă���͓̂����}���ł��B
���̖{�͂`���������搶�̏������{�ŁA
���`�㐔��p���ē���������K���A���_���킩��₷���W�J�������炵���{���Ǝv���܂��B
����ɂ������͍̂��Z���ł����Ƃ��ǂ߂�Ƃ���ł��傤�B���̑��ɂ�
Joseph Rotman�@�gGalois Theory�h
���Ȃ��Ȃ������{���Ǝv���܂��B
���݂͂`���������搶�̂�肱����̕������W���[�ɂȂ����悤�ł��B
���̖{�͖��𑽂����グ�āA���̖��̂Ȃ��Œ�`��疽��������Ă��܂��B
�ł����炱�̖{�͓ǎ҂������l���Ȃ���ΈӖ����Ȃ��Ƃ��������咣���Ă��܂��B
���̈Ӗ��ŋɂ߂ċ���I�Ȗ{�Ƃ�����ł��傤
�i�s�e�Ǝv���Ȃ���B�����ł���������͕͂t����ł��j�B�o�ł͂�͂�Springer�ł��B
�i���W�I�Ȗ{�j
David Eisenbud�@�gCommutative Algebra with a view toward algebraic geometry�h
���̖{�͂W�O�O�y�[�W�ɒB���镪�����{�ł����A
���̗��R�͗��_���ۏ��Ă���l�X�Ȏ����ɑ��āA
���̗��_�����ۂɍ�p���鐔�w�I�ȑΏە��̉�͂����X�ƍs���Ă��邩��ł��B
�܂��ʔ����̂͗��j�I�Ȕw�i���L�`���Ƃ�����Ă��āA���K���A���_�ɂ������G����Ă��܂��B
Miles Reid�@�gUndergraduate Commutative Algebra�h
���̖{���w�ƃ����O�Z�I���[��g�ݍ��킹�������{���Ǝv���܂��B
Undergraduate�Ə̂��Ă��܂������x���͑�w�@���ł��B
�o�ł��Ă���̂�CAMBRIDGE�@UNIVERSITY�@PRESS�Ƃ����Ƃ���ł��B
���̖{�͍ŋߓ��{��o���炵���ł����A�l�͂��܂���{���͊��߂܂���B
�i�����Ɂj
�����Ԃ�ƐF�X�Ȏ����q�ׂĂ��܂����B
���A��X�͌��\���w�̒��S�n�ɂ���̂�������܂���B
���ꂩ���̎����ɂ��Ă͖l���������A�F���i�ޕ��������ł��傤�B
�㐔�������V���[�Y�̏I���ɂ��������������܂����ˁi�j�B
�������ł������H�����ǂ��́A
�ǂޑO�Ƃ��̌�ł͑啪���E���L�������̂ł͂Ȃ��ł��傤���H
�����O�Z�I���[�V���[�Y�̕����i�Q�O�j�������ē��e�̕��͏I���Ƃ������������ł��傤�B
����UFD�Ƃ������悪�����āA���̘b����낤���Ǝv������ł����A
�F�X�Ɩ���������A��߂鎖�ɂ��܂����B
���݂͂���Ɋւ���{�͑����ł�����ˁB
���ꂩ��Noether�ɂ��Ă��u����������ȁc�v�Ǝv���Ă�͂葼�̖{�ɏ��邱�Ƃɂ��܂����B

| NO.799 | 2000.4.8. | ���̗��� | �t�̑S�����Z�싅�i�Q�j |
NO.431�@�t�̑S�����Z�싅�i�P�j�̑����ł��B ���āA����ȃf�[�^�\���悤�Ǝv���Ă����Ƃ��A
�u�N���ɉ����������Ȃ�Z���E���w�̖{�F�H�R�m�i���~�ɕ��Ɂj�v�̖{��ǂ�ł�����A
��ʎ��́A�V�ЂȂǁA�܂�ɂ����N����Ȃ����R�̏o������
�u�|�A�\�����z�v�Ƃ�������Ȋm�����z�̏�Ԃɂ��������ċN����Ƃ����Ă���B mathematica�Ōv�Z�͂��Ă݂܂����B �i�P�j�t�̃Z���o�c �i�Q�j�Ă̑�� �t�]�܂��͏����z�����P�������ς͏t�͂O�D�W�V�P�O��N����A
�Ă͂O�D�U�U�V��N�����Ă��܂��B
��r����ƁA�Ă͏t���A�t�]�܂��͏����z�������Ȃ��������Ƃ��Ӗ����Ă��܂��B
�܂��A�Ă̕������|�A�\�����z���Ă��邱�Ƃ�������܂����B ���Y����͂S���ɁA�g�P�Q�N�t�̑S�����Z�싅�̌��ʂ����̂悤�ɒ��ׂ܂����B �����P�Q�N�̏t�̑��������ׂ܂����B�����������B ���āA���Z�싅�͐��_�̓������e�[�������Ƃ悭�����܂��B
������ɂ��āA���͂��܂����B �������(���Ȃ�H)���邢��������܂��A���`�a�d�͐��O�p�`���Ɨ\�z���Ă��܂��H ���}�̂悤�ɁA�_�`�Ɠ_�a�𒆐S�ɔ��a���`�a�ɓ�����1/4�~�������܂��B ���Y����́A�́A���k���炱��ȑ�w�������̎�����܂����B �P���炎�܂ł̐������������J�[�h���P��������B�������A�����R�Ƃ���B ���P�F ���Q�F (1+2+3+���+n)�(1+2+3+���+n)��W�J����A
�P���炎�̔C�ӂ̂Q�̐ς��Ƃ肤�邷�ׂĂ̏ꍇ��ԗ����Ă���Ǝv���܂��B ���Ғl�d�R(n)�����l�ł��B kiyo����̂��w�E�ŁANO.804�̌v�Z�����������Ƃ���~�X������܂����B ���Ғl�d�Q(n)��(n+1)(3n2-n-2)/12(n-1)�Ƃ���܂����A
����(n-1)�Ŗ��ł��܂��ˁB ���Ғl�d�R(n)�ɂ��ẮA�ꕔ�W����������̂�Y��Ă��܂����B
�����悤�ɂ��āA�Ă̍b�q�������ׂ܂����B
���̌��ʁA�@�͂Q�S�����A�A�͂P�R�����A�B�͂V�����A�C�͂Ȃ��A�D�͂S�����@�ł����B
�����ŁA�ې����̊�͂Q�S�{�V�{�S���R�T
������S�W�Ŋ���ƂR�T�^�S�W���O�D�V�R�E�E�E�@�ō����m���ŏ����Ă��܂��B
����ŁA�Ă��W���N�X�͊m���������܂��B
�܂��A���̊ې����̌��܂����C�j���O�͂P��R��łQ�O����
���̂����@�̃`�[�����P�U�`�[������܂��B
�����āA��Ƃ��āA�t�̃Z���o�c�싅�������Ƃ��ċ����Ă���܂����B
�{�Ɠ����\�������p���܂��B
���Ƃ��Ζ싅�̎������s�����Ƃ�
�u�X�܂ł̂������ɋt�]�܂��͏����z��������N���邩�v�ƌ����p�x���A
�h�܂�ɂ����N����Ȃ����Ɓh�̂P��ł��B
�搧�_���������`�[�������̂܂ܓ������Ă��܂��A�P����t�]�A
�����z�����Ȃ��������ƂɂȂ�B�����ŁA��Ƃ��āA�t�̉��l�Ƃo�k���_�o�߂ł݂܂��B
�P��̕\�̂P�_�͐搧�_������A�����z���Ƃ͌���Ȃ��B
�P��̗��̂Q�_�͋t�]������J�E���g���܂��B
�R��̕\�̂Q�_�͏����z���ł͂Ȃ��̂ŁA�J�E���g���Ȃ����A
�R��̗��̂P�_�͏����z��������J�E���g���܂��B
�U��̕\�̂Q�_�͏����z���ł͂Ȃ��̂ŁA�J�E���g���Ȃ����A
�W��̗��̂P�_�͏����z��������J�E���g���܂��B
�ȏ�A�t�]�܂��͏����z�����Ƃ��ĂR����J�E���g���܂��B
���̓_�����̗��ꁄ�Ɖ̉��߂��قȂ�܂��B
���̐������ł݂�ƁA�{�̒��ł́A�t�̃Z���o�c
�i�ǂ��ǂނƂP�X�X�S�N�̃Z���o�c�̎����̂悤�ł��j�̌��ʂ�
�t�]�E�����z�����N����m�� ���_�l ���ۂ̎�����
�O�� �O�D�T�S�W�R�~�R�P �P�V�D�O�P�Q�W �P�V
�P�� �O�D�R�Q�X�R�~�R�P �P�O�D�Q�O�W�R �P�O
�Q�� �O�D�O�X�W�W�~�R�P �@�R�D�O�U�Q�W �@�R
�R�� �O�D�O�P�X�V�~�R�P �@�O�D�U�P�O�V �@�P
��̕\�̂悤�ł����B�ł́A�ǂ̂悤�ɂ��ă|�A�\�����z�𗘗p���ċ��߂��������܂��B
������ƁA���w�̐��I�Ȏ��ɂȂ�܂����A�|�A�\�����z�̊m�����x����
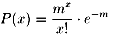 �@�@�ł��B
�@�@�ł��B
�����ŁA���͋t�]�܂��͏����z���̉����A���̓f�[�^�̕��ϒl�ŁA���̏ꍇ��
�����i�P�~�P�O�{�Q�~�R�{�R�~�P�j�^�R�P���O�D�U�P�R�c
����́A���̔N�̃Z���o�c�ł́A�t�]�܂��͏����z�����P�������ςO�D�U�P�R��
�N���������Ƃ��Ӗ����Ă��܂��B
���Y����̎����Ă���X�X�N�x�̏t�A�Ă̋t�]�܂��͏����z���������܂�����A
�t�]�E�����z�����N������ �P�X�X�X�N�x�t�̃Z���o�c �P�X�X�X�N�x�Ă̑��@
�O�@�@�� �P�R���� �Q�S����
�P�@�@�� �P�O���� �P�V�����@
�Q�@�@�� �@�V���� �@�U����
�R�@�@�� �@�P���� �@�P����
�N���|�A�\�����z�����Ă��邩���ׂĂ��������B���肢���܂��B
���Q�l�����F�u�N���ɉ����������Ȃ�Z���E���w�̖{�F�H�R�m�i���~�ɕ��Ɂj���@�@�@�@�@�@�@�@�@�@�@�@�@�@

NO.800
2000.4.8. Junko �t�̑S�����Z�싅�i�R�j
�����i�P�~�P�O�{�Q�~�V�{�R�~�P�j�^�R�P���O�D�W�V�P�O�c
�t�]�E�����z�����N����m�� ���_�l ���ۂ̎�����
�O�� �O�D�S�P�W�T�~�R�P �P�Q�D�X�V�S�X �P�R
�P�� �O�D�R�U�S�T�~�R�P �P�P�D�R�O�O�W �P�O
�Q�� �O�D�P�T�W�W�~�R�P �@�S�D�X�Q�P�R �@�V
�R�� �O�D�O�S�U�P�~�R�P �@�P�D�S�Q�W�W �@�P
�����i�P�~�P�V�{�Q�~�U�{�R�~�P�j�^�R�P���O�D�U�U�U�V�c
�t�]�E�����z�����N����m�� ���_�l ���ۂ̎�����
�O�� �O�D�T�P�R�S�~�S�W �Q�S�D�U�S�S�O �Q�S
�P�� �O�D�R�S�Q�R�~�S�W �P�U�D�S�Q�X�R �P�V
�Q�� �O�D�P�P�S�P�~�S�W �@�T�D�S�V�U�S �@�U
�R�� �O�D�O�Q�T�S�~�S�W �@�P�D�Q�P�V�O �@�P
����ɂ��Ώt�̑��́A�P�R�C�P�P�C�T�C�P�A
�Ă̑��Q�T�C�P�U�C�T�C�P�ł��B
�����������Ă���悤�Ɏv���܂��B

NO.801
2000.4.8. ���̗��� �t�̑S�����Z�싅�i�S�j
�iNO.431�@�t�̑S�����Z�싅�i�P�j�j
�t�̑S�����Z�싅�͐_�ސ쌧�̓��C��w���͍��Z���A���D�����܂����B ���߂łƂ��������܂��B
�܂��A�t�@���ɂƂ��āA�t�]�ɂ��t�]�̎����͖Y����Ȃ�������^���܂��B
�i�P�j���_�������āA���_�ɂ���Ă����̂܂I������������@
�i�Q�j���_�������āA�t�]���āi���_�ɂȂ��Ă��j�I������������A
�i�R�j���_�������āA�t�]����Ă��ċt�]���ďI������������B
�@�ȉ��A���̋t�]�̉ŁA�C�A�D�A�E�ƕ��ނ��Ă����܂��B
������A�ې�������̏ꍇ�͐��_�̓������e�[���������B
�ې����������̏ꍇ�͐��_�̓������e�[���̕����B
�ƂȂ�܂��B���R�A�ې����̑��������ʔ��������Ŋy���ނ��Ƃ��ł������ƂɂȂ�܂��B
������܂ł̂R�P���������̂悤�ɕ��͂��܂����B���̌��ʁA
�@�͂P�U����
�A�͂S����
�B�͂U����
�C�͂Q����
�D�͂R�����@�ł����B
�����ŁA�ې����̊�͂P�U�{�U�{�R���Q�T
������R�P�Ŋ���ƂQ�T�^�R�P���O�D�W�P�E�E�E�@�ō����m���ŏ����Ă��܂��B
����ŁA�W���N�X�͊m���������܂��B
�܂��A���̊ې����̌��܂����C�j���O�͂P��R��łP�V���� ���̂����@�̃`�[�����P�S�`�[������܂��B
�S��U��łT�����A�V��X��łW�����A������̏ꍇ���P�����ł����B
�����ŁA�O��Ɠ������A�싅�̎������s�����Ƃ��u�X�܂ł̂������ɋt�]�܂��͏����z��������N���邩�v�ƌ����p�x���A
�h�܂�ɂ����N����Ȃ����Ɓh�̂P��ł��B
�搧�_���������`�[�������̂܂ܓ������Ă��܂��A�P����t�]�A�����z�����Ȃ��������ƂɂȂ�B
�����ŁA��Ƃ��āA�����P�Q�N�t�̒��H���Z�ƒ��쏤�Ƃ̓��_�o�߂ł݂܂��B
�@
���_�f�� �P �Q �R �S �T �U �V �W �X �v
���@�H �P �O �R �O �P �Q �O �P �O �W
���쏤 �Q �O �O �R �O �O �O �P �~ �U
�P��̕\�̂P�_�͐搧�_������A�����z���Ƃ͌���Ȃ��B�P��̗��̂Q�_�͋t�]������J�E���g�P���܂��B
�R��̕\�̂R�_�͍ċt�]������J�E���g�Q���܂��B
�S��̗��̂R�_�͍āX�t�]������J�E���g�R���܂��B
�T��̕\�̂P�_�͓��_�ŏ����z���ł͂Ȃ��̂ŁA�J�E���g�͂��Ȃ��B
�U��̕\�̂Q�_�͏����z��������A�J�E���g�S���܂�
�ȏ�A�t�]�܂��͏����z�����Ƃ��ĂS����J�E���g���܂��B
���̎�������ԓ����̌����������ł��������Ƃ��Ӗ����Ă��܂��B
�\�ɂ��܂��B�Q�O�O�O�N�Ă̑����������܂��B
�@
�@�t�]�E�����z�����N������ �Q�O�O�O�N�t�̃Z���o�c �Q�O�O�O�N�Ă̑��@
�O�@�@�� �P�U���� �@����
�P�@�@�� �@�V���� �@�����@
�Q�@�@�� �@�T���� �@����
�R�@�@�� �@�Q���� �@����
�S�@�@�� �@�P���� �@����
��̕\���|�A�\�����z�����Ă��邩���݂Ă݂܂��B
������ƁA���w�̐��I�Ȏ��ɂȂ�܂����A�|�A�\�����z�̊m�����x����
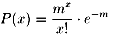 �@�@�@�ł��B
�@�@�@�ł��B
�����ŁA���͋t�]�܂��͏����z���̉����A���̓f�[�^�̕��ϒl�ŁA���̏ꍇ��
�����i�P�~�V�{�Q�~�T�{�R�~�Q�{�S�~�P�j�^�R�P���Q�V�^�R�P���O�D�W�V�P�c
����́A���̔N�̃Z���o�c�ł́A�t�]�܂��͏����z�����P�������ςO�D�W�V�P��N���������Ƃ��Ӗ����Ă��܂��B
�t�]�E�����z�����N����m�� ���_�l ���ۂ̎�����
�O�� �O�D�S�P�W�T�~�R�P �P�Q�D�X�V�S�X �P�U
�P�� �O�D�R�U�S�T�~�R�P �P�P�D�R�O�O�W �@�V
�Q�� �O�D�P�T�W�W�~�R�P �@�S�D�X�Q�P�R �@�T
�R�� �O�D�O�S�U�P�~�R�P �@�P�D�S�Q�W�W �@�Q
�S�� �O�D�O�P�O�O�~�R�P �@�O�D�R�P�P�O�Q �@�P
���Y����́A���̂Q�O�O�O�N�Ă����ׂĂ݂܂��B

NO.802
2000.4.11. Junko �ǂ�ȎO�p�`�H�i�R�j
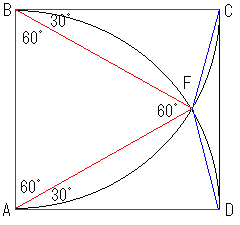
�Q��1/4�~���Ԃ������_���e�Ƃ��܂��B
���`�a�e�͐��O�p�`�ł�����A���p�͂��ׂĂU�O�K�ł��B
���Ɂ��a�b�e�ɒ��ڂ���ƁA�a�b���a�e���ӎO�p�`�ł��邱�Ƃ��킩��܂��B
�ڂb�a�e���R�O�K�ł�����A�ڂa�b�e���V�T�K�ƂȂ�܂��B
�]���āڂe�b�c���P�T�K�ƂȂ�A���͓_�e�͖��ɂ���_�d�ƈ�v���邱�Ƃ��킩��܂��B
�܂聢�`�a�d�͐��O�p�`���Ƃ����킯�ł��B
�ł�������ɂ��遢�`�c�d�͓ӎO�p�`�ł��B

NO.803
2000.4.18. ���̗��� �ς̊��Ғl�i�P�j
���̂����̃J�[�h���疳��ׂɓ����ɂQ���̃J�[�h�����o���Ƃ��A
�����ꂽ���̐ς̊��Ғl�d�Q�i���j�����ŕ\���B
�܂��A�������@�̂Ƃ��́A�d�Q�i���j�^���Q�@���@�H�@�@�����߂�B
���̂����̃J�[�h���疳��ׂɓ����ɂR���̃J�[�h�����o���Ƃ��A
�����ꂽ���̐ς̊��Ғl�d�R�i���j�����ŕ\���B
�܂��A�������@�̂Ƃ��́A�d�R�i���j�^���R�@���@�H�@�@�����߂�B
�ƁA������܂����B�����A�Y�v���o������܂��B�F����I�l���Ă��������B

NO.804
2000.4.21. Junko �ς̊��Ғl�i�Q�j
�������A���������Q���Ђ����Ƃ͂��肦�܂���A12+22+32+���+n2�������˂Ȃ�܂���B
�܂��A1�~2�ƁA2�~1�͓������Ƃł�����A�Q�Ŋ���܂��B
�X�ɁA���ꂼ��̊m���͊F�����ŁA1/n�b2�ł�����A���Ғl�d�Q�i���j��
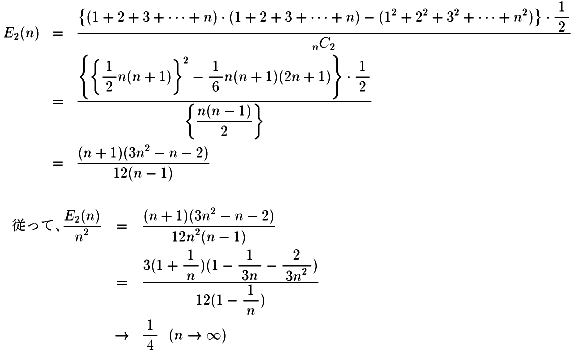
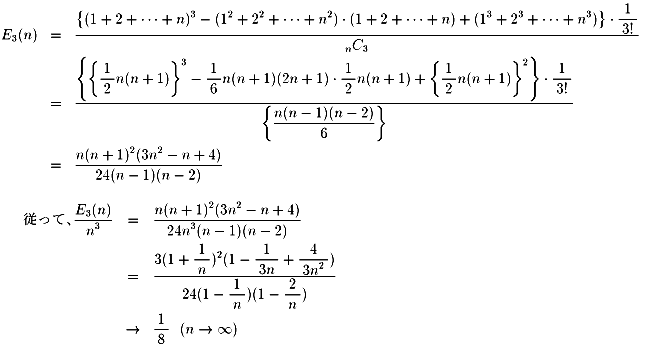

NO.805
2000.4.26. Junko �ς̊��Ғl�i�R�j
���߂Čv�Z�������ĂĂ݂܂��B
�]���āA�d�Q(n)��(n+1)(3n+2)/12
�Ɍ��̕��͉e������܂���B
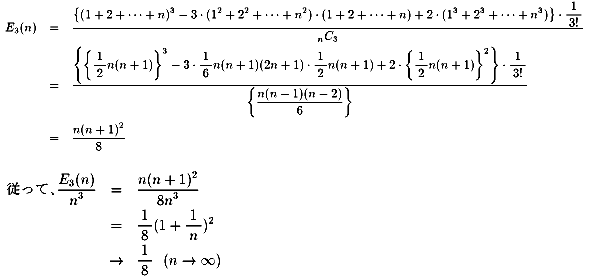

 E-mail
E-mail
 �߂�
�߂�