
���̒l����̓I�ɋ��߂Ă݂܂��傤�B
Weekend Mathematics�^�R���L�E�����^2000.4�`6�^NO.92
| NO.789 | 2000.4.1. | ���̌� | �u�O�p�̖��v�̔��W�i�U�j |
(�ꕔ����4/4 Junko)

���̒l����̓I�ɋ��߂Ă݂܂��傤�B
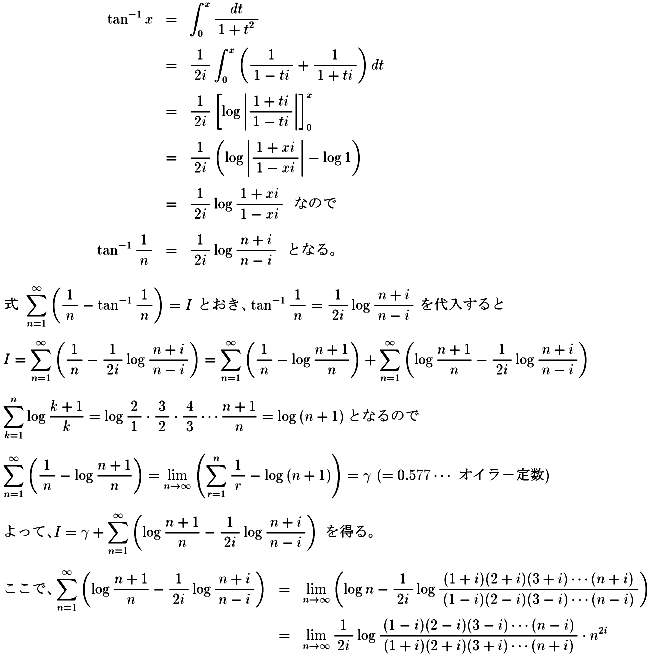

���ہAa=0.498060���,b=-0.154738����ƂȂ�̂�


| NO.790 | 2000.4.2. | ���̗��� | �ǂ�ȎO�p�`�H�i�P�j |
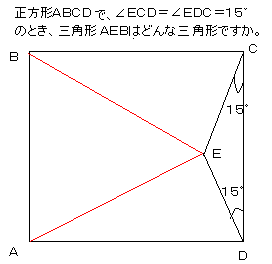
���Y����́A�q�������w����̂Ƃ��A
�u�����`�`�a�b�c�ɂ��āA�ڂd�b�c���ڂd�c�b���P�T�K�̂Ƃ��A
�}�̂悤�ȎO�p�`�`�d�c�͂ǂ�ȎO�p�`�ł��邩�A���ׂāA������ؖ����Ȃ����B�v
�ƁA������܂����B�����A�Y�v���o������܂��B�F����I�l���Ă��������B
���Y����́A�����A�}�̂悤�ȓ_�d��`���čl���Ă݂悤�Ǝv���Ă��܂��B

| NO.791 | 2000.4.3. | WAHEI | �K���A���_�̐S�i�S�j |
�i�Q�̏����^�藝�ƃK���A�̊�{�藝�̌㔼�j
�`���������搶�ɃK���A���_������Ă��炤�O�ɐF�X�������鎖������܂��B
A���W���Ƃ���R�����̓��l�W�Ƃ��܂��傤�B
���̂Ƃ����W��A�^R����邱�Ƃ��ł��܂����B
�܂��ʑ����FA��A�^R�����ia�j��C�ia�j�Œ�߂����͑S�˂ł����B
��������R�Ȏʑ��Ƃ����܂�(natural map)�B
��ʂɎʑ����FA��B��p���ďW��A��ɓ��l�W���߂鎖���ł��܂��B
�q���F���o�ia�A���j��A�~A�b���ia�j�����i���j�p�Ƃ���ƁA
����͖��炩��A��̓��l�W�ŁA���R�Ȏʑ����FA��A�^R�ɂ��Ắ`��R�����藧���܂��B
�i�藝�P�j
�`����łȂ��W���A�q���`��̓��l�W�Ƃ��A���F�`���`�^�q�����R�Ȏʑ��Ƃ���B
�܂��ʑ����F�`���a�i�a���Ӂj�͎��̐��������Ɖ��肷��B
���A�����`�ɑ��A���q���Ȃ���i���j�����i���j�c�i�P�j
���̂Ƃ��ʑ����F�`�^�q���a���������������悤�Ɉ�ӓI�ɒ�܂�B
�i�ؖ��j
�܂��������������]���������������ł��邱�Ƃ������܂��傤�B
�����S�˂Ȃ̂ł`�^�q�̔C�ӂ̌��ɂ��Ă`�̌����K���Ή����Ă��܂��B
�ł�����`�^�q���猳�b�i���j�����āA�b�i���j���b�i���j�����肵�܂��傤�B
����ƕ����̕�肩�炁�q���ł��̂ŁA�i�P�j�̏������炇�i���j�����i���j�ł��B
�ł����炈�i�b�i���j�j�����i�b�i���j�j�ł����Ă��͂�������-�c�������������ł��邱�Ƃ��킩��܂����B
�܂����̂�����ӓI�Ɍ��܂邱�Ƃ������܂��傤�B
����ɂ͂��Ɠ��������������L�����݂����Ȃ炈�����L�ł��鎖�����������ł��ˁB
�͂b�i���j���`�^�q�ɑ����i�b�i���j�j�����i���i���j�j�����L�i�b�i���j�j�B
����Ă������L�ł��B�]���Ă��͂������������悤�Ɉ�ӓI�Ɏ��܂����B�@�@�@�@�@�i�ؖ��I���j
�i���P�j
��̂��ɑ��Ă͎����������B���Ȃ킿�����P�ˁ̂q���q��
�i�ؖ��j
�܂�����P�˂Ɖ��肵�Ăq���q���������܂��傤�B
�q��q���͏W���ł������̂��Ƃ�
�u���v���u���v�������Ηǂ���ł��B
��̒藝�́i�P�j�͂q���q����\���Ă��܂��B
�܂����q�����Ƃ��܂���
���i���j�����i���j�ł����炈�i�b�i���j�j�����i�b�i���j�j�ŁA
���肩�炈�͒P�˂ł�����b�i���j���b�i���j�B
����Ă��q���ł��B����łq���q���������܂����B
���ɂq���q�������肵�Ă����P�˂ł��邱�Ƃ������܂��傤�B
���i�b�i���j�j�����i�b�i���j�j�͂��i���j�����i���j�������Ă��܂����炁�q�����ł��B
���܂q���q����肁�q���ł�����b�i���j���b�i���j���������A
�����P�˂ł��邱�Ƃ������Ă��܂��B�@�@�@�@�i�ؖ��I���j
���̂��Ƃ��玟�̃R�������[�܂��B
�i�R�������[�P�j
��͂��̒藝�̂��ɂ����āA���������S�˂ŁA�q���q���Ȃ�A���͑S�P�˂ł���B
�����Ńt�@�N�^�[�O���[�v�ɂ��Ă���Ă����܂��傤�B
�f���Q�A�m�����̐��K�����Q�Ƃ����Ƃ��m���f��ɒ�߂�Q�̓��l�W
�q�P�Ƃq�Q�͈�v���܂����B
�f�^�q�P���f�^�q�Q�ł����A
������f�^�m�Ə����Ăf�̂m�ɂ��t�@�N�^�[�O���[�v�Ƃ����܂��B
���Ȃ킿�f�^�m���f�^�q�P���f�^�q�Q�ł��B
���Ȃ݂ɂ��̂f�^�m�̉��Z�͎��ł��܂���܂�܂��B
���m�E���m���i�����j�m
���̉��Z�����������]�c�������������ł��邱�ƂƁA
���̉��Z�ɂ���Ăf�^�m���Q�ɂȂ邱�Ƃ͊F����ɔC�����ق��������ł��傤
�i����͂��Ђ���Ăق����B���̍ہA�P�ʌ��Ƌt���ɓ��ɒ��ӂ��Ă��������j�B
�f�^�m�͌Q�ƂȂ�܂�����A�ʑ����F�f���f�^�m�͂��i���j�����m�ŌQ�̏����^�ʑ��ɂȂ�A
�S�˂ł��B����͖{���I�Ɏ��R�Ȏʑ��ł��ˁB
���̂��ɂ��Ă͊ʑ��̎��Ɠ��l�A�j�����i���j���m�����藧���܂��B
�i�藝�Q�j
���F�f���f�L���Q�̏����^�ʑ��Ƃ��A�m���f�̐��K�����Q�łj�����i���j�Ɋ܂܂����̂Ɖ��肷��B
���̂Ƃ����F�f�^�m���f�L�Ȃ鏀���^�ʑ������i���m�j�����i���j�ƂȂ�悤�Ɉ�ӓI�Ɍ��܂�B
�i�ؖ��j
�藝�P�����܂��g���܂��B
���͓��l�W�Ƃ��Ăq�Q���̗p���܂��傤
�i�������q�P�ł�����ɍ����x������܂���j�B
���q�Q���Ƃ��܂��ƁA
�����]���m�ł�����m���j�����i���j�ɒ��ӂ��Ă��i�����]�j�����L
�i�����ł��L�͂f�L�̒P�ʌ��j
�ł����āA���͏����^�ʑ���肇�i���j�����i���j���������B
����Ē藝�P�́i�P�j�̏����������̂ŁA
�������i���m�j�����i���j�Ȃ�悤�Ɉ�ӓI�Ɍ��܂�B
���ꂪ�����^�ʑ��ł��邱�Ƃ́A
���i���m�E���m�j�����i�i�����j�m�j�����i�����j�����i���j���i���j�����i���m�j���i���m�j
�ł��邱�Ƃɏ]���܂��B������₂�͂f�̔C�ӂ̌��ł��B
�@�@�@�@�i�ؖ��I���j
�i�R�������[�Q�j
���F�f���f�L���Q�̏����^�ʑ��Ƃ���B
���̂Ƃ����F�f�^�j�����i���j���f�L�ŁA�͂����f�ɑ����i���j�����i���j�j�����i���j
���������^�ʑ�����ӓI�ɑ��݂���B
���ɂf�^�j�����i���j�`�h���i���j�ł���B
�u�R�������[���ĉ��ł����H�v�Ƃ������������������܂��B
�u�R�������[�v�Ƃ́u�n�v�̂��Ƃł��B
�܂肠�錋�ʁi�藝�j������ꂽ�ہA�������炷���ɓ������u���Y���v�Ƃ����܂��B
�ł�����R�������[�̏ؖ��͏Ȃ����̂����ʂł��B
�l���R�������[�̏ؖ��͈Öق̂����ɊF����ɔC���Ă��鎖�������ł��B
�ł��A��̃R�������[�Q�̏ؖ��͂Ȃ��Ȃ�����Ƃ��낪�����̂ł���Ă����܂��傤�B
�Ƃ���ŁA�Q�̏����^�ʑ����F�f���f�L�ɂ����āA
�j�����i���j�F���o�����f�b���i���j�����L�p�ł��B
�i�R�������[�Q�̏ؖ��j
�܂��A�j�����i���j���f�̐��K�����Q�ł��邱�Ƃ������܂��傤�B
�j�����i���j���m�Ƃ����܂��ƁA�͂����f�ɑ��āA
���m���m�������������Ƃ������Ƃł����A
��ʂɂf���Q�Ƃ��m�����̐��K�����Q�Ƃ���Ǝ��̕�肪���藧���܂��B
�i���Q�j
�m���f�̐��K�����Q�̂��m���]���m�i�͂����f�j
���̕����܂������܂��傤�B
�m���f�̐��K�����Q�Ɖ��肵�܂��B
�̓������m���]�����ƁA�����������]�Ə����܂��B
������͂m�̌��ł��B
���K�����Q�̒�`����m�̌��͂f�̑S�Ă̌��Ɖ��Ȃ̂�
�����������]���������]�������������m�B
����Ă��m���]���m�ł��B
�t�ɂ��m���]���m�����肵�܂��傤�B
����Ɓ͂����m�ɑ��āA�������]�����P�Ƃm�̌����P�����܂��B
�ł����炁�������P���ƂȂ��Ă��m���m���B
����i���]�j�]�����ɒ��ӂ��āi�Q�x�t�������ƌ��ɖ߂�j�A
�m�̔C�ӂ̌����ɑ��āi���]�j�]���i���]�j�����Q�Ȃ�
�m�̌����Q�����݂��܂��B
���̂��Ƃ���i���]�j���Q�����i���]�j�ƂȂ���
���͔C�ӂ����炁�]�����߂Ă��Ə��������ł��Ăm�������m�B
����Ă��m���m�����f�̔C�ӂ̌����ɂ��Đ��藧���A�m�͐��K�����Q�ł��B�i���̏ؖ��I���j
���āA���̕����g���Ƃj�����i���j���f�̐��K�����Q�ł��邱�Ƃ͂����ɂ킩��܂��B
�m���j�����i���j�Ƃ����Ă��邱�Ƃɒ��ӂ��āA�͂������]�����m���]������Ă��ňڂ��ƁA
���i�������]�j�����i���j���i���j���i���]�j�����i���j�����i���j�]�����i���j���i���j�]�����B
����Ă������]���m�ł���������j�����i���j���m�͂f�̐��K�����Q�ł��B
�ł�����藝�Q��菀���^�ʑ����F�f�^�j�����i���j���f�L�����i���j�����i���j�j�����i���j
�����悤�Ɉ�ӓI�Ɍ��܂�܂��B
����ɂ��i���j�����i���j�Ȃ�����]���j�����i���j�Ȃ̂ŕ��P�ɂ�肱�̂��͒P�˂ł��B
�܂��ʁF�f�^�j�����i���j���h���i���j���ʁi���j�����i���j�j�����i���j�Œ�߂��
����͖��炩�ɑS�˂ł�����A�ʁ����ɒ��ӂ��Ă��͑S�˂ł��B
����Ă��͏����^�ʑ��őS�P�˂ł�����A�f�^�j�����i���j�`�h���i���j�����藧���܂��B
�i�R�������[�Q�̏ؖ��I���j
���F�q���r���ʑ��Ƃ��܂��Ƃq�`�r�Ƃ͂����S�P�˂ɂȂ邱�Ƃł����B
�Q�̃��x���ł��S�������ł��B
���Ȃ킿���F�f���f�L���Q�̏����^�ʑ��Ƃ���Ƃf�`�f�L�Ƃ�
�����S�P�˂ɂȂ邱�ƂȂ̂ł��B
���ꂩ�獡�������R�������[�Q�̎����Q�̏����^�藝�Ƃ����܂��B
�ł́A���悢��`���������搶�̂��o�܂��ł��B�F����A���Â��ɁB
�i�K���A�̊�{�藝�̌㔼�cfundamental Galois theorem stage2�j
�O�����l��K�^F��L�����̃K���A�g��Ƃ���B
A��E��H��B���K���A�̊�{�藝�̑O���őΉ����������ԑ̂ƕ����Q�Ƃ���B
���̎��A�����������B
�i�ؖ��j
�`���������搶�ǂ������肪�Ƃ��������܂����i����j�B
�`���������搶�ɂ͂܂���œo�ꂵ�Ă��������܂��B
��͂菭�����x�ł��ˁB
�{���͗\���ύX���ăK���A�̊�{�藝�̌㔼�͂�炸�ɁA
�����ɉ��Q�̐����ɓ����Ă��܂������Ǝv������ł����A
�����Ď��グ�Č��邱�Ƃɂ��܂����B
���āA�O��ؖ��������Ɏg���Ă��܂����x�N�g����Ԃ̐���
�i�����ɂ͘A���������̐����j���ؖ����Ă��܂��܂��傤�B
����͌��ݏo�ł���Ă��邠������`�㐔�̖{�ɂ͕K���o�Ă��܂�����A
�������炻�̂܂ܔ������܂��B
�i���j
�̂j�̌����W���Ƃ��A���P�A���Q�A�c������
���m���Ƃ���A��������
| ���P�P���P�{���P�Q���Q�{�c���P���������O |
| ���Q�P���P�{���Q�Q���Q�{�c���Q���������O |
| �@�@�@�@�@�c�c |
| �����P���P�{�����Q���Q�{�c�������������O |
�i�ؖ��j
�������ׂĂ̌W�����O�Ȃ�A
�Ⴆ���P���P�Ǝ���̂ŁA�����������ɂȂ�B
�]���ĈȌ�O�łȂ��W��������Ɖ��肷��B����Ă��P�P���O�Ƃ��Ă悢�B�����ŁA
�k���������P���P�{�����Q���Q�{�c����������
�Ƃ����B
����ɍŏ��̎��A�k�P���O�̗��ӂɂ��P�P�̋t���A
���P�P-�������邱�Ƃɂ��A
���P�P���P�Ɖ��肵�Ă悢���Ƃ��킩��
�i�̂�����A�������������ł���킯�ł��j�B
�����ŘA���������i���̘A�����������i�P�j�Ƃ����j
| �k�P���O |
| �k�Q�|���Q�P�k�P���O |
| �@�@�c |
| �k���|�����P�k�P���O |
| �k�Q�|���Q�P�k�P���O |
| �@�@�c |
| �k���|�����P�k�P���O |
�i���Q�j
�l���i���j�m���i���j�j��L�����̑̂̊g���Ƃ���Ɓi�]���Ă��������L���j�A
�m�j�F�l�n���������������B
����͑̂̊g��Ɋւ����{�I�Ȍ��ʂȂ̂ł��ЂƂ��ؖ����Ă��������ł��B
�i���Q�̏ؖ��j
�j�̈�g�̊��A�o���P�A���Q�A�c�����p������Ă��܂��B
���܁m�j�F�m�n�����ł�����A���̂悤�ɂ���������킯�ł��ˁB
�j�̑S�Ă̌��͂��̃��P�A�c�����̈ꎟ�����Ƃ��Ĉ�ӓI�ɏ����܂��B
���Ȃ킿�A�͂����j�́A���������������A�i�P���������j�ƈ�ʂ�ɏ����܂��B
�����ŁA�W�����P�A�c�����͂m�̌��ł��B
�m�m�F�l�n�����ł�����A��͂�m�̈�g�̊��A
�o���P�A���Q�A�c�����p������
�m�̔C�ӂ̌��͂��̊��̈ꎟ�����Ƃ��Ĉ�ʂ�ɏ����܂��B
�ł����炃�P�A�c�����͂��̃��P�A�c������
�ꎟ�����ŏ�����킯�ł��B
�܂�A
���r�������r�v���v�A�i�P���v�����j
�Ə����܂��B
�����ł�������r�v�͂l�̌��ł��B
����Ă����j�͂������i���r�v���v�j���r��
�����r�v���v���r�ł��B
���������Ăj�̑S�Ă̌��͂����̌��̈ꎟ�����ł�����鎖���킩��܂����B
�����̒�`����A���Ǝ����̂͂��̂����̌����l��ꎟ�Ɨ��ɂȂ��Ă��邱�Ƃł��B
�����r�v���v���r���O�Ƃ��܂��ƁA
���r�������r�v���v�͂m�̌��ł�����
���r���m��ňꎟ�Ɨ��Ȃ̂Ł͂��ɂ���
���r���O�������r�v���v�B
���v�͂l��ꎟ�Ɨ��Ȃ̂Ł͂��ɑ��āA
�܂�͂��A���ɑ��Ă��r�v���O�B
����ő�ӂ͖�������܂����B�@�@�@�@�@�i�ؖ��I���j
���̏ؖ��͂���Ȃɕ��G�ł͂Ȃ��A�ꎟ�Ɨ���A���̈Ӗ�����������ƒ͂�ł���A
��`�ɉ����ؖ��ł��B
����͓��e����⑽���Ȃ����̂ł����܂łɂ��āA����͉��Q���`���܂��B
���Ƃ����̂́u���������ł���v�Ƃ����Ӗ��ł����A
������Q�Ƃ͂��������ǂ�ȌQ�Ȃ̂ł��傤���H
�܂����ꂪ��������㐔�I�Ɂu�����v�Ƃ������Ƃǂ̂悤�Ɋւ���Ă���̂ł��傤���H
������ӂ̎���𗝘_���A����������̂�����̓��e�ł��B

| NO.792 | 2000.4.3. | �ӂ����� | �ǂ�ȎO�p�`�H�i�Q�j |
�܂��A30���A60���A90���̒��p�O�p�`abc���l���܂��B
��a�̓�����������bc�Ƃ̌�_��d�Ƃ���ƎO�p�`adc��
15���A75���A90���̒��p�O�p�`�ɂȂ�܂��B
�����Ŋp�̓����ɂ�����藝���bd:dc��ab:ac�ƂȂ�̂�
���̂��Ƃ��ac:dc�A�܂�15���A75���A90���̒��p�O�p�`��
�ΕӂłȂ����ӂƒZ�ӂ̔䂪�P:2- �ƂȂ邱�Ƃ��킩��܂��B
�ƂȂ邱�Ƃ��킩��܂��B
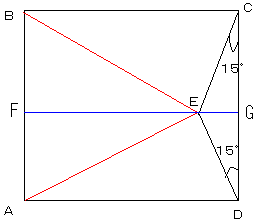
�i���̐����`�ŁA�_E��ʂ�悤�ɕ�BC�̕��s���������A
���̕��s���ƕ�AB�Ƃ̌�_��F�A��CD�Ƃ̌�_��G�Ƃ��ĉ������B�j
�����`�̕ӂ̒������Q�Ƃ���Ə�̂��Ƃ��EG��2- �ƂȂ�̂�
FE��2-(2-
�ƂȂ�̂�
FE��2-(2- )��
)�� �ƂȂ�A
�ƂȂ�A
BF��1���
�O�p�`BFE��30���A60���A90���̒��p�O�p�`�ƂȂ�܂��B
���O�p�`AEB�͐��O�p�`
������Ɨ͋Z�̂悤�ȋC�����܂����A���Y��������w����ƌ����Ă����̂�
���w�����ۂ��������ł�����ł���ˁB

| NO.793 | 2000.4.4. | ���̌� | ���Z�p�`�̖��E�Â� |
�挎�����Z�p�`�̖���̉ł��B
���߂����͕��f�����g���Ėʐϔ���o����肩���ł��B
���̖��������ʂ��ʉ����Ă݂܂����B
�����p�`�̕ӂ�a:b�ɕ����Ă��̓����_������ŏo���鏬���p�`�Ƃ̔�����߂܂����B
�����p�`�^�傎�p�`��Rn(a:b)�Ƃ�����
Rn(a:b)=(a2+2abcos(2��/n)+b2)/(a+b)2
����̖��ł͂���6�Aa:b=1:3�Ȃ̂�R6(1:3)=13/16�ƂȂ�A
����13:16�ł��B

| NO.794 | 2000.4.4. | �g�V | �o�Ȑ��� �i�P�j |
�����O�̂Ƃ��̂���cosh ���̂̋t����
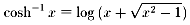
�ŁC�����S�����̂Ƃ��̂���cosh ���̂̋t����
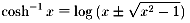
�Ȃ�ł��傤���H

| NO.795 | 2000.4.5. | �g�V | �o�Ȑ��� �i�Q�j |
�o�Ȑ����̒�`����
�o�Ȑ��̔C�ӂ̓_(x�Cy)�ƌ��_�̂Ȃ��p���ƂƂ����Ƃ�
(x�Cy)��(cosh x�Csinh x)�ƒ�`������Ă��ƂȂ�ł����H
����Ƃ��C
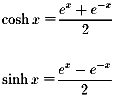
�Ƃ�����Ă��ƂȂ�ł����H

| NO.796 | 2000.4.5. | Junko | �o�Ȑ��� �i�R�j |
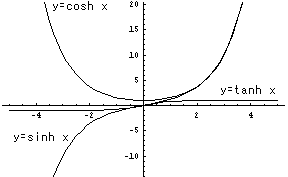
�o�Ȑ���(hyperbolic function)�́A�ȉ��̂悤�ɒ�`����܂��B
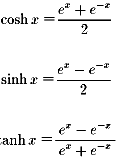
�O���t�͉E�̂悤�ɂȂ�܂��B
���̊��́A�������낢���ƂɎO�p���Ɏ��������������Ă��܂��B
��`���炷���킩��悤�ɁAy=cosh x �͋���Ay=sinh x ,y=tanh x �͊���ł��B
[�Q�l]����F��(��)����(�|��)�@�@�@�@����F�F��(��)���|��(�|��)�@

 E-mail
E-mail
 �߂�
�߂�