
Weekend Mathematics/コロキウム室/2000.1〜3/NO.84
| NO.731 | 2000.2.1. | WAHEI | リングセオリー(8) |
NO.726 リングセオリー(7)でJunko先生は環写像のカーネルが環Rのイデアルであること
を調べてくれました。それについての僕の考えです。
解く方法は全く申し分ありませんが、イデアルの定義に従って、一応カーネルエフが
空集合でない事を確認しておきましょう。
まず、f:R → Sを環写像としましょう。
Ker(f)={a∈R|f(a)=0}でした。
環写像の性質からf(0)=0です。
ですから、0∈Ker(f)となって、Ker(f)は空ではないことがわかります。
また、イデアルの定義の2番目をよく見てください。
スカラーは広いRから取らねばなりません。
Junko先生は惜しい事にKer(f)の中だけで考えてしまいました。
∀α∈R、∀a∈Ker(f)を取ってきます。そしてαaをfで移してみます。
f(αa)=f(α)f(a)
となり、a∈Ker(f)ですからf(a)=0従って上の式は
f(αa)=f(α)f(a)=f(α)0=0 (0には何を掛けても0なので)
よってf(αa)=0となり、αa∈Ker(f)です。
和のほうはJunko先生のやり方で申し分ありません。ですからKer(f)はRのイデアルで
ある事がわかります。

| NO.732 | 2000.2.2. | WAHEI | リングセオリー(9) |
今回の目標はイデアルを味わった後に群論からの追加項目を踏まえてファクターリン
グの概念を得る事にあります。
まずイデアルの復習ですが、イデアルとは可換環Rの空でない部分集合で和について
閉じていてかつ、環Rから取った勝手な元についての積について閉じているという事
でした。
イデアルの定義は非常に簡単ですが、この定義の成す単純さと、それから出
てくるイデアルの多様性は不思議な対象性を成しています。
イデアルの定義から次の事がすぐにわかります。
(イデアルの基本性質)
Ωを可換環Rのイデアルであるとすれば、次が正しい。
ここでイデアルの例を考えてみましょう。
整数全体をZで表します。
Zは数の足し算と掛け算で環でした。
ここで環であることを強調するためにZのことを「整数環」と呼ぶ事にしましょう。
我々が知っている環はそう多くありません。
ですからこの整数環は今のところ我々にとって命綱のようなものですから
大切にしなくてはなりません。
今後抽象的な環がいくつか登場してきますが、我々は抽象化されすぎてよくわか
らなくなったときには常にこの整数環に立ち戻って考える事にしましょう。
さて、(n)={nχ|n∈Z、χ∈Z n≧2}と定義します。
もちろんnχは数の掛け算ですが、この(n)は良くわかるようにn
の倍数の集合ですね。
また、nは2以上の整数ですから1は(n)には入っていません。
従って、NO.722 リングセオリー(3)の補題によると、これは全体(すなわちZ)と一
致しないという事もわかります。
かつ、この(n)はZのイデアルになっています。
なぜならば、もちろん(n)≠φであって、∀a、b∈(n)を取ると(n)の定義
からa=nχ、b=nyという顔をしていて
a+b=nχ+ny=n(χ+y)
となり、χもyも整数ですから括弧の中も整数です。
ですからa+bもnの倍数となり、(n)の元です。
一方、∀α∈Zに対して、αa=α(nχ)=(nχ)α=n(χα)∈(n)
(χα∈Zなので)
よって(n)はZのイデアルです。
ですから上に書いたイデアルの基本性質は全て満たします。
ここでイデアルの基本性質の(3)を見てください。
何か思い出す事はないでしょうか?
環Rと言うのは和でアーベル群でした。代数方程式シリーズでも説明しましたが
群には部分群という大事な概念がありました。
ΩをRのイデアルとするとΩは空でなくて、かつ∀a、b∈Ωに対して、
基本性質の(3)から、a−b∈Ωです。
これはイデアルΩが環Rの部分群である事を言っています。
ただし演算は和です。
(NO.706 代数方程式の代数的解法(4)では演算は積で表していましたが、
それを和に変えただけです)
部分群を用いる事で母体の群に2つの同値関係を定める事ができました。再掲してお
きますと、
R1={(a、b)|−a+b∈Ω}
R2={(a、b)|a−b∈Ω}
です。但し今は可換環Rを群と見なしています。注意してください。(定義から環は
和でアーベル「群」なのですから、そう見なしても何ら矛盾は生じません)
このR1とR2をよくよく眺めてみるとR1=R2となっている事に気が付くと思い
ます。
さあ、代数方程式シリーズでは不本意ながら書くことができなかった正規部分群につ
いて書くときが来ました。
(定義)
群Gに対してその部分群Hが正規部分群(normal sub group)であるとは
∀a∈Gに対してaH=Haが成り立つ事を言う。
復習ですがaH={ah|h∈H}でした。
Haについても同様です。
上の定義はaHとHaが集合として等しいとき、HをGの正規部分群であると呼ぼうというこです。
もう少し丁寧に観てみますと、任意のGの元と可換な部分群を正規部分群と言うのです。
この事からすべてアーベル群の部分群は正規部分群となっている事がわかります。
するとどうでしょう?可換環Rは和でアーベル群でした。ですからその部分群である
イデアルは和で正規部分群を成している事がわかります。
またイデアルに関してはR1=R2でした。
(イデアルと環の定義からすぐ出てきますので確かめてください。
でも頭の中でできてしまうかもしれません)実はこの事実は一般化できます。
(命題)
Hを群Gの正規部分群とするならばR1=R2が成り立つ事が必要にして十分であ
る。
(証明)
群論のレベルに戻って証明します。従って演算は積とします。
まずHを群Gの正規部分群とします。
aR1bとするとa‐b∈H。
よってHの元hを用いてa‐b=hと書け、従ってb=ah∈aH=Ha(仮定から)ですので
b=ka(k∈H)と書けます。
ですからba‐=k∈HとなってbR2a。
R2は同値関係ですのでaR2bとなって、R1⊆R2
全く同様にしてR2⊆R1も示せますから、暇なときにでも確かめておいてくださ
い。よってR1=R2です。
今度は逆を示します。
つまり、R1=R2を仮定してHが正規部分群である事を示します。
示すべきはaH⊆Haかつ、Ha⊆aHです。
(確認しておきますが、2つの集合が等しいと言う事はこういうことでした。)
∀χ∈aHを取るとχ=ah(h∈H)と書けます。
これはaR1χを意味しますから仮定によってaR2χとなり、従ってaχ‐∈Hです。
HはGの演算で群ですから(aχ‐)‐=(χ‐)‐a‐=χa‐∈Hです。
(群だから、当然逆元も入っている)
これはχ∈Haを意味します。ですからaH⊆Ha。
さて、次は∀y∈Haを取ってくるとy=ka(k∈H)と書けて、よってyR2aより仮
定からyR1aで従ってy‐a∈H。
Hは群なので(y‐a)‐∈H⇔a‐y∈Hで
これはy∈aHを表しています。ですからHa⊆aH
∴aH=Ha (証明終わり)
この事から可換環R上にそのイデアルΩが定める同値関係R1とR2は等しいということ
がわかりました。つまり、RのR1による商集合とR2による商集合は一致します。商集
合と言うのは同値関係によって1つの集合がバラバラに分割されるわけですが、その
破片(ピース)の集合でした。
(詳しくはNO.709 代数方程式の代数的解法(7)を見てくだ
さい)
ここでR/R1=R/R2ですがこれをR/Ωと書くことにします。これを可換環Rのイデア
ルΩによるファクターリング(factor ring)といい、日本語では商環と言います。
ではR/Ωの演算はどのように定めたらいいでしょうか?
また、それ以前にR/Ωの元はどのような形をしているのでしょうか?
今まで準備した事を使えば簡単にわかりま
すが、それにしてもR/Ωの内部構造については次回に詳しく考えて見ましょう。

| NO.733 | 2000.2.3. | ヴァー | 2000年の問題・その後 |
1月の問題(2000年の問題)の解答編にあるJunko先生の最後の御質問の件ですが,
「カバリエリの原理」とか,または「パップス・ギュルダンの法則」というものと
関係があると思います.
細かいことはわからないので,現在調べている最中です.
一応,速報ということで.

| NO.734 | 2000.2.3. | WAHEI | リングセオリー(10) |
まずは復習です。
和と積で整数を一般化した代数を可換環といいました。
これにより、体のところで出てきた準同型写像が矛盾なく定義され、
それを特に環写像と言ったのでした。
また、その環写像が全単射のとき、これを環同型といいました。
さらに環の部分環とは単位元を共有し、母体の環の和と積について独立した環を成す
のもでした。
ちなみに母体の環が可換環であればその部分環も可換環です。
最近気が付いたことですが、「環というと可換環である」という固い信念を持った人
を見かけます。
しかし環の定義というのはそうではなくて、必ずしも積に対する可換
性を仮定しませんでした。ですから、以前は環と書いたら可換環とするといいました
が、やはり厳密に区別する事とします。でも、以下に出てくる環は大体可換環ですか
ら、安心してください。
さて、同値関係に関する次の重要な補題を証明しておきましょう。
(分割の補題)
集合A(≠φ)とA上の同値関係Rについて、次の3つは同値である。
(補題の証明)
3つの事柄が互いに同値であることを言うのは(1)⇒(2)、(2)⇒(3)、
(3)⇒(1)の流れで示せばいいのです。
まずは(1)⇒(2)です。
C(a)=C(b)ですからC(a)∩C(b)=C(a)です。
(もちろんC(b)としても構いません)
従いましてRは同値関係ですからaRaです。
よってa∈C(a)なのでC(a)∩C(b)≠φ。
次に(2)⇒(3)です。
C(a)∩C(b)が空集合ではないので何か元が取れます。
それをχとしましょう。
χ∈C(a)かつχ∈C(b)なので、χRaかつχRbです。
ですからRが同値関係である事を観ればaRbです。
最後に(3)⇒(1)です。
∀χ∈C(a)を取るとχRaです。仮定からaRbですのでχRbです。(Rは同値関係だから)
よってχ∈C(b)でC(a)⊆C(b)です。
今度はC(b)から任意にyを取ってきます。
するとyRbで仮定のaRbからbRaなのでyRa。
よってC(b)⊆C(a)となりますのでC(a)=C(b) (証明終わり)
単純な事実ですがこれは今後の基本的な手法となりますのでキチンと理解してください。
さて、可換環Aが与えられていてそのイデアルΩを考えます。
ΩはAの和で正規部分群でした。前回示したようにR1=R2です。
これからその商集合を考えるとA/R1=A/R2でこれをA/Ωと書こうということでした。
これをファクターリングと言うのですが、
我々はまだこれが環の構造を持つ事を具体的に記述していませんから、
今のところは単なる商集合です。
何とかしてこれに環構造をもたせたいのですが、手がかりはA/ΩはA/R2と等しいと言う事です。
(もちろんA/Ω=A/R1とみても構いません)
A/R2の定義はR2による同値類の集合でした。
つまり集合の集合で、数学ではこの「集合の集合」のことを集合族と呼んでいます。
ですからA/R2は集合族なのですが、集合の間に和と積など定義できるのでしょうか?
集合の積とは一体なんでしょう?
この疑問に答えるためにまずはA/R2の元(これは集合)を具体的に書き出してみる必要があります。
定義から
A/Ω=A/R2={C2(a)|a∈A}です。
ところでC2(a)={χ∈A|a−χ∈Ω}でした。
このようなχについては
a−χ∈ΩですのでΩの元αを用いてa−χ=αと書けます。
よってχ=a−α=a+(−α)で改めて−αをαとかくと
(Ωはイデアルでαはイデアルの元ですから−α∈Ωでこれをαと書くという意味です)
χ=a+αとなります。
ここでa+Ω:={a+α|α∈Ω}としますと、χはこのa+Ωに属しています。
ただし、ここで使った記号「:=」は左辺を右辺で定義すると言う意味です。
今後良く使いますから覚えておいてください。
わかったことはC2(a)⊆a+Ωです。
逆の包含関係もいえます。これは皆さんに任せます。確かめてみてください。
つまりA/Ωの元はR2による同値類なのですがこれはa+Ωという格好をしている事が
明らかになって大分見やすくなりました。
C2(a)のままでは抽象的で良くわからなかったかもしれませんが、
実はそれがa+Ωとなるように同値関係R2を決めたのです。
代数方程式シリーズで群のレベルでR2に関する同値類がHaとなるのを観ました。
(Hは群Gの部分群)これは演算が積ですがこれを和にすりかえて見ますとH+aです。
可換環は和でアーベル群ですからH+a=a+Hが成り立ちます。
まさにこれはa+Ωですね。ですから今まで述べてきた事は本質的に新しい事ではなくて
もう我々の知識を有機的に駆使すれば確かめる事ができます。
(明らかになった事)
上で考察したように可換環AのイデアルΩによる商集合の各元というのは同値類です
が、それはa+Ω(∀a∈A)と言う格好をしている事がわかりました。次第にA/Ωの
構造が明らかになってきましたね。
次にやるべき事はこのA/Ωに和と積を定めてやる事です。
ここで注意してほしい事は演算と言うのは環の定義(NO.717 リングセオリー(1)を参照)でも
述べたように直積からそれ自身への写像でした。ですから集合の和と積なんて途方も
ないことできっこないなんて絶望する事は全くなくてキチンと定める事ができます。
どのように定めるかと言いますと、次のように定めてはどうでしょうか?
∀a+Ω、b+Ω∈A/Ωに対して、
(和) (a+Ω)+(b+Ω):=(a+b)+Ω
(積) (a+Ω)(b+Ω):=(ab)+Ω
このように定めてみますと、これが写像として矛盾なく定義されている事がわかります。
ところで「矛盾なく定義されている」と言う言葉は英語ではwell-defined といいます。
どこかで聞いた言葉ですね。そう、写像の3番目の条件でした。そこで問題です。
(問題1)
上で定めた和と積が写像としてwell-definedである事を確かめてください。
(ヒント:well-definedである事をいうので
a+Ω=a’+Ω、b+Ω=b’+Ωを仮定して
(a+b)+Ω=(a’+b’)+Ω
(ab)+Ω=(a’b’)+Ω
を示せば言い訳です。その際a+Ωやb+Ωなどが同値類であることを考えてみてください)
(問題2)
上で定めた和と積でA/Ωが可換環となることを示してください。ところでA/Ωの単
位元とゼロ元は何ですか?
問題1ができれば問題2は機械的に可換環の定義をチェックするだけです。
もちろん分割の補題を使って構いません。
(ただし分割の補題を必ず自分で1回ぐらいは確か
めてください。確かめると言う事は紙と鉛筆で自分の手を動かすと言う事ですよ)
この問題は僕も考えてみます。皆さんも考えてみてください。前にも書きましたが解
けても、解けなくても、また間違えても一向に構いません。自分の考えを表現してく
ださい。
次回は一応この問題は認めて先へ進みます。
従ってA/Ωのことを商集合とはいわずファクターリングと言っていいでしょう。
この問題についての僕の考えはその次ぐらいに書きたいと思います。

| NO.735 | 2000.2.5. | WAHEI | リングセオリー(11) |
(環写像のイデアルに対する作用)
ここではイデアルが環写像によってどのように移るのかを考察しましょう。
f:R → Sを環写像とします。またΩをRのイデアルとしましょう。
f(Ω):={f(a)∈S|a∈Ω}とし、これをΩの像と言う事にしますと、
このf(Ω)はもはやSのイデアルにはなっていない事がわかります。
なぜならば写像fによって可換環Sのスカラーがうまく制御できないのです。
f(Ω)がSのイデアルならば∀α∈Sについて
αa∈f(Ω)(a∈f(Ω))ですが、Rの元が全てSへ移っているとは限らないので
これは一般に言えません。
でも簡単な条件を付け加えれば幸いにしてf(Ω)をSのイデアルにすることができます。
その条件とは他でもなく環写像が全射になることなのです。
fが全射ならばその定義よりIm(f)=Sですのでスカラーがうまく制御できます。
実際に確かめてみると
∀α∈Sについてfが全射なのでRの元bに対してf(b)=αです。
だから∀a∈f(Ω)をとってくると定義からc∈Ωでa=f(c)と書けて、
αa=f(b)f(c)=f(bc)∈f(Ω)です。(ΩはRのイデアルなのでbc
∈Ωだから)
和の方は普通にできます。それからΩ≠φよりf(Ω)≠φです。
以上によって環写像fが全射ならばイデアルはイデアルに移る事がわかりました。
(原像について)
f:R → Sが環写像であるならば、Im(f)はSの部分環になり、これをイメージ
エフと言ったのでした。これに双対する概念として原像の概念があります。
Sの部分集合Kについて、このKの原像を次で定義します。
f‐(K):={a∈R|f(a)∈K}
つまり移してKに入るRの元の集合で、これは明らかにRの部分集合です。
ここで書いたf‐は逆写像とは意味が違います。注意してください。
さて、やりたい事はSのイデアルΩの原像がRのイデアルになっている事です。
定義からf‐(Ω)={a∈R|f(a)∈Ω}です。
まずこれが空でないことを確かめます。0∈Rで環写像の性質からf(0)=0でΩ
はイデアルですからイデアルの基本性質より0∈Ω。
よって0∈f‐(Ω)ですから、f‐(Ω)は空ではありません。
また∀a、b∈f‐(Ω)を取ってくると定義からf(a)、f(b)∈ΩでΩはイ
デアルよりf(a)+f(b)=f(a+b)∈Ωです。(環写像の定義はバンバン
使って構いません)従ってa+b∈f‐(Ω)です。
一方、∀α∈R、∀a∈f‐(Ω)に対してf(αa)=f(α)f(a)
であって、αが任意なのでf(α)もSの任意の元、またf(a)∈Ωであり、Ωは
Sのイデアルですから、f(α)f(a)∈Ω。よってαa∈f‐(Ω)。
∴f‐(Ω)はRのイデアルになっている事がわかりました。この事については環写
像fが全射である必要はありません。単に環写像であればいいのです。そうすればイ
デアルの原像はイデアルになります。
(まとめてみると)
(問題1)
可換環RのいくつかのイデアルA,B,・・・・Cについて、その共通部分A∩B∩
・・・・∩CはRのイデアルであることを確かめてください。
これは定義に従ってやっていけば、比較的簡単にできると思います。
(問題2)
可換環Rのいくつかの元a1、a2、・・・・・anについて
(a1、a2、・・・・・an):=
{a1α1+a2α2+・・・・+anαn|αk∈R、1≦k≦n}
はRのイデアルであることを確かめてください。
この問題もイデアルの定義をチェックするだけですが、なかなか豊富な理論体系が含
まれています。
この(a1、a2、・・・・・an)を
a1、a2、・・・・・anで生成されるイデアルといいます。
そしてa1、a2、・・・・・anaを生成元というのです。
特に1つの元で生成されるイデアルを単項イデアルといいます。つまり単項イデアルとは
(a):={aα|α∈R、a∈R}です。
すぐわかりますが生成元はそれらが生成するイデアルに含まれています。
また有限個の生成元で生成されているイデアルを有限生成イデアルといいます。
イデアルが有限生成である環と言うのは比較的扱いが簡単で現在でも活発に研究されています。
(定義)
全てのイデアルが単項イデアルである可換環を単項イデアル環という。
任意のイデアルが単項ならばその環は驚くほど整った環です。
後で「単項イデアル整域」という可換環を考えますが、この定義はそれの一歩前です。
じつは整数環は単項イデアル環です。
これについての詳しい記述は次回、環の元の種類を定義しつつ考えてみましょう。

| NO.736 | 2000.2.6. | 水の流れ | 野球の貯金(1) |
太郎さんは、大の巨人ファンであることはもう皆さん!ご存じでしょう。
昨年セ・リーグを制した中日ドラゴンズはシーズン135試合を通して、
常に、勝ち星が負け星を上まわっていました。
いわゆる貯金があったのです。
さて、今年ジャイアンツが(a+b)試合戦って、勝ち数がaで、負け数がbであったとします。
そして、この(a+b)試合中、常に貯金の状態(勝ち星が負け星を上まわっていて、
勝ち負けが同数は除く)で勝敗の推移の仕方の確率を求めたくなりました。
すなわち、a>bである。ここで、問題です。
問題1:
a=3,b=2で終わる確率を求めてください。
問題2:
a=4,b=2で終わる確率を求めてください。
問題3:
常に貯金の状態、勝ち数がaで、負け数がbで終わる確率を求めてください。
問題4:
一般の場合から、今年ジャイアンツが、a=77,b=58で終わる確率を求めてください。
太郎さんは、早速、問題1,問題2で、実際に勝ち負けを書いてみてようと思っています。

| NO.737 | 2000.2.6. | WAHEI | リングセオリー(12) |
(Zornの補題と整列定理)
少し予定を変更してZorn補題について考えてみましょう。
これは補題という名がついていますが、もう公理として追加すべき物です。
代数方程式シリーズで選択公理について考えてみました。
じつはあれと、このZornの補題というのは同値なのです。
しかしこのZornの補題というのは選択公理よりも多少くどい言い回しをしなければなりま
せんから、単純な選択公理と同値であることに不思議さを感じるかもしれません。
でも、本質を捉えていれば簡単な事です。まずはいくつかの言葉を定義します。
(定義1)
Aを空でない集合とする。「≦」がA上の順序であるとは、以下の3つを満たす事を言う。
- ∀a∈Aに対してa≦a
- ∀a、b∈Aに対してa≦bかつb≦aならばa=b
- ∀a、b、c∈Aに対してa≦b、b≦cならばa≦c
(定義2)
集合Aが順序集合であるとは上の順序が少なくとも1つ定められている集合をいう。
(定義3)
集合Aが全順序集合であるとは∀a、b∈Aについてa≦bまたはb≦aが成り立つ順序 集合を言う。
(定義4)
順序集合Aの部分集合BについてBの任意の元bについてあるAの元aが存在し、b≦aと なっているときBは上に有界であるという。
また、Bの元yに対し、このyを真に上から押さえ込むBの元が存在しないとき、この yをBの極大元という。
(定義5)
順序集合Aの部分集合CがchainであるとはCが全順序集合である事をいう。
(Zornの補題)
順序集合A内のあらゆるchainが上に有界であるならば、Aは少なくとも1つの極大元を持つ。
(整列定理)
Sを空でない集合とする。このときSにうまく順序を定めればSを整列集合にすること ができる。但し、整列集合とは全順序集合でかつ最小元をもつものである。

| NO.738 | 2000.2.8. | kiyo | 野球の貯金(2) |
パスカルの三角形が関係していると思います。
n=a-b とする。
| a>b=1 | n 通り |
| a>b=2 | n(n+3)/2 通り |
| a>b=3 | n(n+5)(n+4)/6 通り |
| a>b=4 | n(n+7)(n+6)(n+5)/24 通り |
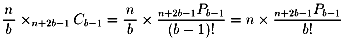
全体の場合の数を2
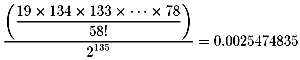
となると思います。

 E-mail
E-mail
 戻る
戻る