Weekend Mathematics／問題／問題37

３７．２０００年の問題

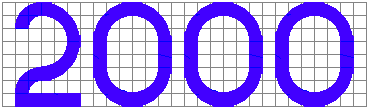
上の図は、最小の正方形の一辺の長さが どれも１である格子に、２０００の数字が描かれたものです。
これらの数字の部分の面積の総和はどれだけになるでしょうか。 ただし、曲線の部分はすべて円周の一部とします。

解答・その１

（ペンネ−ム：青光）

この問題は以下の青色の部分の面積を求めるのが問題です。正方形の辺の長さはどれも１辺１です。


以下、円周率はπを使います。

まず　　の面積を求めます。
これは、　…[１] 　　…[２]　 　…[３]　 　…[４] の４つの部分からできているので、それぞれの面積を求めると、

[１]：半径２の円から、内側半径１の円を除いた物の４分の１……（２^２π−１^２π）×１／４ ＝ ３π／４
[２]：半径３の円から、内側半径２の円を除いた物の半分　　……（３^２π−２^２π）×１／２ ＝ ５π／２
[３]：[１]と同じなので、面積は３π／４
[４]：長方形　……　１×５＝５

となるので、これらの合計を求めると、　３π／４ ＋ ５π／２ ＋ ３π／４ ＋ ５ ＝ ５＋４π　となります。

次に　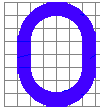　の面積を求めます。
これも同様に分割して考えると 　…[１]　 　…[２]　 　…[３]　の３つの部分からできているので、それぞれの面積を求めると、

[１]：半径３の円から、内側半径２の円を除いた物の半分　　……（３^２π−２^２π）×１／２ ＝ ５π／２
[２]：長方形の面積が １×２＝２ それが２つあるので、 ２×２＝４
[３]：向きが反対だけど[１]と同じ、面積は５π／２

となるので、これらの合計を求めると、　５π／２ ＋ ４ ＋ ５π／２ ＝ ４＋５π　となります。

よって、求める面積は、 （５＋４π）＋ ３（４＋５π）＝ １７＋１９π となって、これが求める答えになります。

答え １７＋１９π


と、解いてみましたが、なんか「力押し」って感じがします。もっと良い解き方があるのかな？

解答・その２

（ペンネ−ム：浜田　明巳）

数字２の部分に，

• 半径２の半円から半径１の半円をひいた図形と，
• 半径３の半円から半径２の半円をひいた図形と，
• 縦横が１，５の長方形

• 半径３の円から半径２の円をひいた図形と，
• 縦横が２，１の長方形が２個

解答・その３

（ペンネ−ム：かに）

数字２の面積は４π＋５、０は５π＋４
したがって面積の総和は
（４π＋５）＋（５π＋４）×３＝１９π＋１７

解答・その４

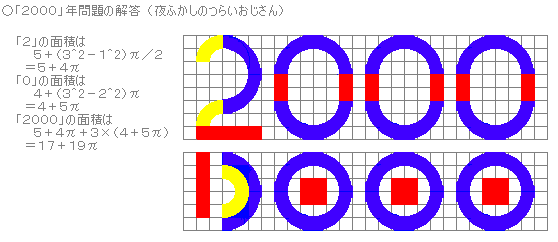
（ペンネ−ム：夜ふかしのつらいおじさん）

解答・その５

（ペンネ−ム：ぺっとんとん）

答え「19π+17」

• 円周部分その1・・・2の右側と、0の上下
  
• 円周部分その2・・・2の左側
  
• 直線部分
  

又は黒い部分の軸の長さを計算して、19π+17
幅が1なので、1×（19π+17）＝19π+17

解答・その６

（ペンネ−ム：sambaGREEN）

道幅が一定の道の面積は，道の中心線の長さ×道幅で求められます。
道幅は１ですから，中心線の長さの合計を求めればよいことになります。

• 文字「２」　直径５の半円，　直径３の４分円×２個，　直線　５
• 文字「０」　直径５の半円×２個，　直線　２×２本

「簡単すぎて不安です．また何か落とし穴があるのでしょうか？」 という感想をいただきましたが、そういうことではありません。
(そう思っていただけるというのは、うれしい限りですが・・・。)
今回の問題は言ってみれば２０００年のご祝儀問題でして、 お正月休みにのんびり計算できる問題・・・と思ったのです。

青光さんの解答・その１からは、 htmlでしかも解説図つきの解答をいただきました。どうもありがとうございます。
夜ふかしのつらいおじさんの解答・その４では、私のへたな図を鮮やかに 組み替えて解いていただきました。

sambaGREENさんの解答・その６の中にある
「道幅が一定の道の面積は，道の中心線の長さ×道幅で求められます。」
という記述ですが、円周の場合はもちろん当然です。
ぺっとんとんさんの解答・その５も同様のアプロ−チですね。

ところでこれは、円周以外の一般に曲線についても言えることでしょうか？
感覚的には正しいと思いますし、きっと正しいでしょう。
しかし任意の曲線についての証明はどうなっているのかなあと気になります。
「道幅が一定」というあたりから定義していく必要がありそうですね。
どなたかご存知の方、よろしくお願いします。
（まとめになってない？）

関連した話題が、コロキウム室 NO.733 にあります。

E-mail 戻る