コロキウム室

まずは前回(NO.717)の補足をします。以下環と書いたら可換環とします。
集合Rを環としましょう。このとき次が成り立ちます。

1. ０a＝a０＝０　（∀a∈R、０はもちろんRの０）
2. （−a）ｂ＝a（−ｂ）＝−aｂ
3. −a＝（−１）a
4. （−a）（−ｂ）＝aｂ
5. a（ｂ−ｃ）＝aｂ−aｃ

ｆ：R → Sを環写像とする。このとき

1. ｆ（−a）＝−ｆ（a）
2. ｆ（a−ｂ）＝ｆ（a）−ｆ（ｂ）

また、環の例を少し紹介したいと思います。
R＝Z×Qを整数と有理数の直積とします。
このRに次で演算を入れて見ましょう。
まず和を次で定めます。
（a、ｘ）＋（ｂ、ｙ）＝（a＋ｂ、ｘ＋ｙ）
但しa、ｂは整数でｘ、ｙは有理数です。また右辺の括弧の中の＋は数の＋です。
そして積を次で定めましょう。
（a、ｘ）（ｂ、ｙ）＝（aｂ、aｙ＋ｂｘ）
やはり右辺の積は数の積、和は数の和です。
まずこれが演算になっている事はいいでしょう。
a＋ｂは整数同士の足し算ですから やはり整数でｘ＋ｙも有理数同士の掛け算なのでやはり有理数です。
ですから（a、ｘ）＋（ｂ、ｙ）∈Rです。
積のほうも明らかにR上の演算になっています。 またこれが環の定義を満たす事は腕力（計算力）です。 全てきちんとやっておきましょう。
（a、ｘ）＋（（ｂ、ｙ）＋（ｃ、ｚ））＝（（a、ｘ）＋（ｂ、ｙ））＋（ｃ、ｚ）
はZもQも和でアーベル群だから自明。
（０、０）∈Rで∀（a、ｘ）∈Rに対して
（a、ｘ）＋（０、０）＝（０、０）＋（a、ｘ）＝（a、ｘ）はやはり自明。
よって（０、０）がRの０となっている。
（a、ｘ）＋（ｂ、ｙ）＝（ｂ、ｙ）＋（a、ｘ）もZとQが和でアーベル群であること からOK。
また∀（a、ｘ）∈Rに対して（−a、−ｘ）∈Rで両者足すと（０、０）となる。
以上よりRは上で定めた和によってアーベル群。

	（（a、ｘ）（ｂ、ｙ））（ｃ、ｚ）
＝	（aｂ、aｙ＋ｂｘ）（ｃ、ｚ）
＝	（（aｂ）ｃ、（aｂ）ｚ＋ｃ（aｙ＋ｂｘ））
＝	（aｂｃ、aｂｚ＋ｃaｙ＋ｃｂｘ）（a、ｘ）（（ｂ、ｙ）（ｃ、ｚ））
＝	（a、ｘ）（ｂｃ、ｂｚ＋ｃｙ）
＝	（a（ｂｃ）、a（ｂｚ＋ｃｙ）＋（ｂｃ）ｘ）
＝	（aｂｃ、aｂｚ＋aｃｙ＋ｃｂｘ）

よって、結合律はOK
また

	（a、ｘ）（（ｂ、ｙ）＋（ｃ、ｚ））
	（a、ｘ）（ｂ＋ｃ、ｙ＋ｚ）
	（a（ｂ＋ｃ）、a（ｙ＋ｚ）＋（ｂ＋ｃ）ｘ）
	（aｂ＋aｃ、aｙ＋aｚ＋ｂｘ＋ｃｘ）（a、ｘ）（ｂ、ｙ）＋（a、ｘ）（ｃ、ｚ）
	（aｂ、aｙ＋ｂｘ）＋（aｃ、aｚ＋ｃｘ）
	（aｂ＋aｃ、aｙ＋aｚ＋ｂｘ＋ｃｘ）

よって分配律が成り立っている。
また（a、ｘ）（ｂ、ｙ）＝（aｂ、aｙ＋ｂｘ）で
（ｂ、ｙ）（a、ｘ）＝（ｂa、ｂｘ＋aｙ）＝（aｂ、aｙ＋ｂｘ）より積について可 換であるから、
（（a、ｘ）＋（ｂ、ｙ））（ｃ、ｚ）＝（a、ｘ）（ｃ、ｚ）＋（ｂ、ｙ）（ｃ、ｚ）は確かめることなく成り立つ。
さらに、（１，０）∈Rで∀（a、ｘ）∈Rについて、
（１，０）（a、ｘ）＝（１a、１ｘ＋a０）＝（a、ｘ）
よって（１、０）がRの１となっている。 ですから、Rは環です。

この例のように環とは創ろうと思えば結構創る事ができる対象で、自分の手に触れる 事ができる貴重な数学的対象といえるでしょう。 上の例は基本的には数の和と積を用いています。 ですから、本質的には数の世界にある環といえます。 （もしかしたら上の例で計算ミスをしているかもしれません。 自分で確かめる際は注意してください）
ここで皆さんも自分で環を創ってみてください。 いろいろできるかと思います。 我々がよく知る環（整数や有理数、実数、行列など）の部分環を創ってみてもいいと思います。 部分環ならば環となりますし、（ただし母体としている環の和と積で）部分環 の定義は環の純粋な定義よりも簡単ですからね。 （従って、部分環を考える事は環論では非常に重要になってきます）

さて、ここでイデアルについて考えてみましょう。まずはイデアルの定義です。

（定義）
Ω（オメガと読みます）が環ＲのイデアルであるとはΩは空でないＲの部分集合で次 の２つを満たす事を言う。

1. ∀ａ、ｂ∈Ωに対して、ａ＋ｂ∈Ωである。
2. ∀α∈Ｒ、∀ａ∈Ωに対してαａ∈Ωである。

余談ですが、イデアルというのは横文字で書けばｉｄｅａｌですが、これは英語の発 音によるとアイデアルとか言います。しかし数学ではドイツ語風にイデアルと読みま す。これを創った人がドイツ人だったのでしょうか？僕はどうもそんな気がします。
１９９４年に解決されたフェルマー予想の歴史でこのイデアルという概念が生まれた のだそうです。フェルマー予想についてはいろいろな本が出版されていますので興味 のある方は読んでみるといいかと思います。 （このフェルマー予想の正しい証明は現在たった１つしか知られていません）

NO.717 リングセオリー（１）では環写像ｆを用いて環Ｒの中にＫｅｒ（ｆ）を定義しました が、実はこれはＲのイデアルになっています。確かめてみてください。
それから次の補題を証明しておきましょう。

（補題）
１∈Ω⇔Ω＝Ｒ 但し、Ｒは環でΩはＲのイデアルとする。

（証明）
１∈Ωを仮定する。Ωはイデアルなので∀α∈Ｒを取ってくると１α＝α∈Ωである から、Ｒ⊆Ωである。またイデアルの定義からΩ⊆ＲだったのでＲ＝Ω 逆は１∈Ｒ＝Ωから自明。
イデアルの定義だけからは１∈Ωはわからないわけですが、もしイデアルが１を含め ば母体のＲと一致してしまうというのです。これを用いると環Ｒの部分集合であるＫ ｅｒ（ｆ）の大きさが大体わかります。
もし１∈Ｋｅｒ（ｆ）ならば、定義よりｆ（１）＝０ですが、ｆは環写像なのでｆ （１）＝１です。
よって１＝０となり、環の定義（１≠０）に矛盾します。
だから、１はＫｅｒ（ｆ）に入っておらず、補題からＫｅｒ（ｆ）≠Ｒとなり、Ｋｅ ｒ（ｆ）はＲの真の部分集合という事がわかります。つまりＫｅｒ（ｆ）⊂Ｒです。

次回はこのイデアルをじっくりと味わって、さらに環論を展開していきましょう。

NO.717 リングセオリー（１） の中の例１について考えてみます。

（例１）
ｆ：C → C
を複素数から複素数への写像とする。
ただし対応はｆ（a＋bi）＝a−biとする。
また、これは環同型か？

f(α)f(β)	=f(a＋bi)f(c＋di)
	=(a-bi)(c-di)
	=(ac-bd)-(ad+bc)i

f(αβ)	=f{(a＋bi)(c＋di)}
	=f{(ac-bd)+(ad+bc)i}
	=(ac-bd)-(ad+bc)i

これより、f(αβ)=f(α)f(β)であることがわかります。

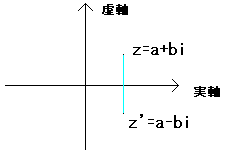
全単射であることは、 ｆ（a＋bi）＝a−bi より、複素平面で上下をひっくり返すということで 、厳密にやらずに許してもらいましょう。

従って、これは環同型であるといえます。

NO.717 リングセオリー（１） の中の

ｆ(R)（Im(ｆ)ともかきます。）はSの部分環となっていますが、Ker（ｆ）はRの部分環にはなっていません。

ｆ(R)についてです。 NO.717 リングセオリー（１）の中にある部分環の定義に従って示していきます。

1. Ｒ≠φ ならば、当然ｆ(R)≠φ です。
   
2. ∀a、ｂ∈ｆ(R)とすると、
   ｆ(α)＝ａ、ｆ(β)＝ｂなるα、β∈Rが存在する。
   
   ｆは準同型写像であるから、
   ｆ(α＋β)＝ｆ(α)＋ｆ(β)＝ａ＋ｂ
   ａ＋ｂの逆像 α＋β∈R　が存在するから、ａ＋ｂ∈ｆ(R)
   
   また、ｆ(αβ)＝ｆ(α)ｆ(β)＝ａｂ
   ａｂの逆像 αβ∈R　が存在するから、ａｂ∈ｆ(R)
   
   更に、ｆ(−α)＝−ｆ(α)＝−ａ・・・(注)
   −ａの逆像 −α∈R　が存在するから、−ａ∈ｆ(R)
   
   
3. ｆは準同型写像であるから、ｆ(１)＝１
   １∈ｆ(R)
   

Ker（ｆ）はRの部分環にはなっていません。
なぜなら、ｆは準同型写像であるから、ｆ(１)＝１≠０です。
従って、１はKer（ｆ）の元ではありません。
単位元を持ちませんから、部分環とはいえません。

(注)については、次のNO.725にて。

NO.722 リングセオリー（３）の中の

ｆ：R → Sを環写像とする。このとき

1. ｆ（−a）＝−ｆ（a）
2. ｆ（a−ｂ）＝ｆ（a）−ｆ（ｂ）

が正しい。

1. ｆは準同型写像であるから、
   ｆ(ａ)＋ｆ(−ａ)＝ｆ(ａ＋(−ａ))＝ｆ(０)＝０
   従って、ｆ(−ａ)＝−ｆ(ａ)
   
2. 同様に、
   ｆ(ａ−ｂ)＋ｆ(ｂ)＝ｆ((ａ−ｂ)＋ｂ)＝ｆ(ａ)
   ｆ(ａ−ｂ)＝ｆ(ａ)−ｆ(ｂ)
   

NO.722 リングセオリー（３）の中の

環写像ｆを用いて環Ｒの中にＫｅｒ（ｆ）を定義しました が、実はこれはＲのイデアルになっています。

1. ∀ａ、ｂ∈Ｋｅｒ（ｆ）とすると、 ｆ(ａ)＝０、ｆ(ｂ)＝０であり、ｆは準同型写像だから、
   ｆ(ａ＋ｂ)＝ｆ(ａ)＋ｆ(ｂ)＝０＋０＝０
   従って、ａ＋ｂ∈Ｋｅｒ（ｆ）である。
2. 同様に
   ｆ(ａｂ)＝ｆ(ａ)ｆ(ｂ)＝０・０＝０
   従って、ａｂ∈Ｋｅｒ（ｆ）である。

第４３回数学的な応募問題

太郎さんは、大の巨人ファンです。2000年の今年は長嶋監督の最後の年になるかもしれません。
是非、連勝を重ねてリーグ優勝をと願っています。
ｎ試合野球を戦って、勝敗表を見てみます。 このとき、２連勝以上している確率ａ(ｎ)について、次の問に答えてください。
ただし、お互いに戦うときの勝つ確率は互角とし、引き分けはないものとする。

問題１：
ｎ＝１、２、３のとき、２連勝以上している確率ａ(ｎ)を求めよ。

問題２：
漸化式を考えて、一般の場合の確率ａ(ｎ)を求めよ。

皆さん！　家で、途中使ってあるビデオカセットのテープの残り何分録画出来るか 考えてことがありますか。 では、具体的に問題を提示します。
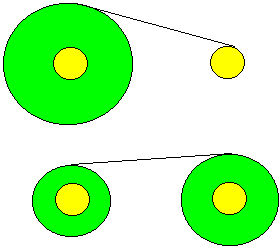
ここに、160分のビデオカセットテープがあります。 最初は内系が半径５ｃｍで、外系の半径が１５ｃｍありました。 ここから、すでに録画済みのがあって、途中をみてみると、 外系の半径を測ったらちょうど、10ｃｍになっていました。 ここで、

問題１：
今、もう一方の録画済みのテープの外系の半径を求めよ。勿論、同じ大きさのリールです。

問題２：
これから、最後まで録画を撮りたいのですが、何分録画可能でしょう。

断面の面積で考えます。

問題１：
１５^２π−５^２π＝ (１０^２π−５^２π)−(ｘ^２π−５^２π)
これより、ｘ^２＝１５０、

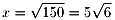
問題２：
１５^２π−５^２π：(１０^２π−５^２π) ＝１６０：ｙ
２００：７５＝１６０：ｙ
ｙ＝１６０×(７５／２００)＝１６０×(３／８)＝６０(分)

(一部修正　1/31,20:00)

第４４回数学的な応募問題

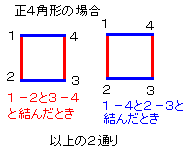
太郎さんは、円に内接している正２ｎ角形を描いています。
この図形の頂点をｎ組のペアに分ける方法の中で、 それぞれのペアを結ぶｎ本の線分が互いに交わらないように分ける方法を考えてみました。
この分け方の方法をｆ(n)としたとき、次の問題に答えてください。
ただし、ｆ(０)＝１，　ｆ(１)＝１と便宜上します。
また、ｎ＝２ときは参考に図に書いておきます。ここから、ｆ(２)＝２になっています。

問題１：
ｎ＝３，４のとき、ｆ(n)を求めてください。

問題２：
ｆ(n)の漸化式を作って、一般項ｆ(n)をｎで表してください。

太郎さんは、早速、正６角形や。正８角形を描いて考えてみようと思っています。

E-mail 戻る