Weekend Mathematics／コロキウム室／1999.4〜6／NO.64

コロキウム室



NO.546 '99 6/27月の光オイラーの「無限解析入門（１）」（２０）


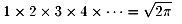
この式は初めて見たので驚きました。 早速証明に取り掛かりましたがまだ出来ていません。 そのかわりこの式を仮定して別の奇妙な式が得られました。

２×３×５×７×１１×・・・＝1/４π2

左辺は素数の無限積です。

証明）


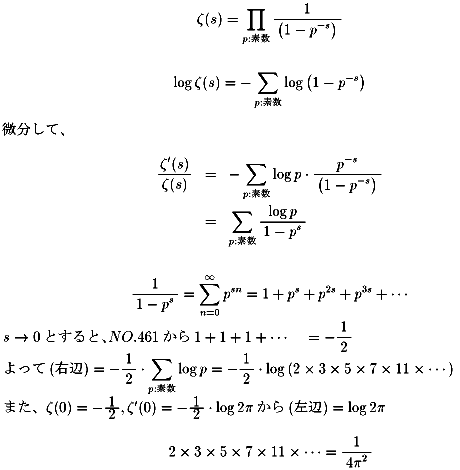
証明終）



NO.547 '99 6/27月の光素数定理

素数定理の証明ではありませんが、 素数定理が正しいと思わせる計算を紹介します。
NO.385で



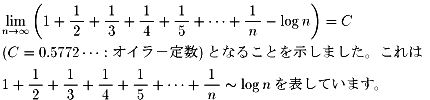
そしてNO.405でも述べられているように、 オイラー流の書き方をすると






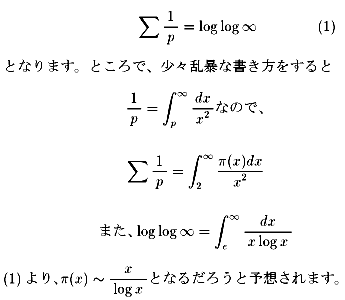
NO.548 '99 6/27水の流れ特製のサイコロ（１）

第２０回数学的な応募問題

太郎さんには、中学校に通っている子供がいます。 先日、学校で数学の授業に、折り紙でサッカーボールを 作ったり、正八面体や正十二面体の模型を厚紙で作ってきました。
そのとき、立方体の展開図を作ってきて、各面に正の整数を書き入れて、 ２つのサイコロを作る宿題がありました。 ただし、２個のサイコロを投げたとき、目の和の出方が普通のサイコロと同じようで あるような特製のサイコロということでした。 ここで、普通のサイコロとは当然１から６までの整数が目としてあるものです。 だから、２つのサイコロは同一ある必要はないですし、その目が６以下である必要もない。 また、すべて異なる目である必要もありません。

問題１：普通の２個のサイコロを投げて、目の和の出方を考えてください。

問題２：今、オイラーの業績について、いろいろ研究しています。 このオイラーの偉大なアイディアは、 整数の性質を調べるのにベキ級数を使ったことです。
そのアイディアは、整数ａとｂとを加えることが累乗 ｘａとｘｂを掛けることに対応することにあります。 そこで、次の整式を展開して係数をみてください。

（ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６）２

問題３：上の事実を利用して、宿題の特製のサイコロの展開図に、正の整数を入れてください。

太郎さんも童心にかえって、いろいろと数字を書いていましたが、なかなかうまくいきません。 皆さんも、考えてください。　



NO.549 '99 6/27水の流れ連続根号数・その２（２）

NO.268で提起された問題です。


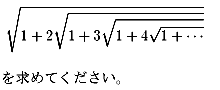
解法　この数字の規則性から



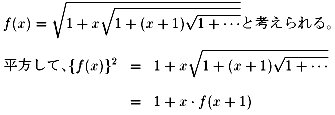
この関数方程式を満たすf(x)が解である。整関数で見つけてみます。
f(x)=a0xn+a1xn-1+･･･とおくと (a0≠0)
左辺の最高次の次数は2n次、一方、右辺の次数は(n+1)次
よって、2n=n+1　　　従ってn=1
ここで、f(x)=ax+bとおいて代入すると(a≠0)
(ax+b)2=1+x{a(x+1)+b}
a2x2+2abx+b2=ax2+(a+b)x+1
係数を比較して解くと、a=1,b=1
従って、f(x)=x+1
次に元に戻して、
与式=f(2)=2+1=3　　(答)
ただし、整関数以外にもしもあったとしても、値としては変化しない。



　
NO.550 '99 6/28Junko同窓会（２）

その会合に集まった人の人数をNとすると、 各人が知っている人の数は1〜N-1の(N-1)通りになります。
一方メンバ−はN人いるのですから、その中には知っている人の人数が等しい人のペアが最低１組はできてしまうわけです。



　
NO.551 '99 6/28Junko特製のサイコロ（２）

問題１
  １２３ ４５６
１ ２３４ ５６７
２ ３４５ ６７８
３ ４５６ ７８９
４ ５６７ ８９１０
５ ６７８ ９１０１１
６ ７８９ １０１１１２


問題２

　（ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６）２
＝（ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６）・ （ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６）
＝（ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６＋ｘ７）＋ （ｘ３＋ｘ４＋ｘ５＋ｘ６＋ｘ７＋ｘ８）＋ （ｘ４＋ｘ５＋・・・）＋・・・


ここに現れてくる指数は上の表をまったく同じ！になります。

問題３

２つのさいころの和として同じものを期待するならば、 この結果を変えずに(項数６の整式)・(項数６の整式)の別な組み合わせを探せばいいのではないかと考えました。
＝（ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６）・ （ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６）
＝ｘ（１＋ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５）・ ｘ（１＋ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５）
＝（１＋ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５）・ （ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６＋ｘ７）

すぐにこのやり方が思い浮かびます。
２つのさいころは指数を読んでいけばいいので、「０，１，２，３，４，５」と「２，３，４，５，６，７」です。
しかしながらこれは片方を減らして片方を増やす、和としては一定。 自明だけれど、おもしろくない、第一０はだめですし・・・。（問題の作成者はその辺をよくわかっていらっしゃる。）
そこで、ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６ の因数分解を考えました。
項数６（６＝２×３の合成数）のこの式は次のように分解できます。
ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６ ＝ｘ（１＋ｘ＋ｘ２）（１＋ｘ３）

ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６ ＝ｘ（１＋ｘ）（１＋ｘ２＋ｘ４）

どちらも完全な因数分解ではありませんが、ｘ・（項数２）・（項数３）という形に２通りの分解ができるという ところがミソです。 これを組み替えて、（項数６）・（項数６）という形を作ります。
＝（ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６）・ （ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６）
＝ｘ（１＋ｘ＋ｘ２）（１＋ｘ３）・ｘ（１＋ｘ）（１＋ｘ２＋ｘ４）
＝ｘ（１＋ｘ＋ｘ２）（１＋ｘ）・ｘ（１＋ｘ３）（１＋ｘ２＋ｘ４）
＝（ｘ＋２ｘ２＋２ｘ３＋ｘ４）・ （ｘ＋ｘ３＋ｘ４＋ｘ５＋ｘ６＋ｘ８）
＝（ｘ＋ｘ２＋ｘ２＋ｘ３＋ｘ３＋ｘ４）・ （ｘ＋ｘ３＋ｘ４＋ｘ５＋ｘ６＋ｘ８）

というわけで２つのさいころを、「１，２，２，３，３，４」と「１，３，４，５，６，８」とすればいいということがわかります。
和を表にしたものを下に示します。

  １３４ ５６８
１ ２４５ ６７９
２ ３５６ ７８１０
２ ３５６ ７８１０
３ ４６７ ８９１１
３ ４６７ ８９１１
４ ５７８ ９１０１２






NO.552 '99 6/29水の流れ同窓会（３）

Ｎｏ５５０の考えは、「鳩の巣の原理」という考え方です。

＜ｎ、ｋは自然数とする。 合計（ｋｎ＋１）羽以上の鳩がｎ個の鳩の巣のいずれかに入っているとき、 少なくとも１つの鳩の巣には（ｋ＋１）羽以上の鳩が同居している。＞
このような考え方です。 数学は、抽象的な命題を具体的な分かりやすいことと対応させて、 考えてみることも大切です。



　
NO.553 '99 6/29Junkoオイラーの「無限解析入門（１）」（２１）

NO.544を受けて、
F(x)=(1+x)(1+x2)(1+x3)(1+x4)･･･
=1+x+x2+2x3+2x4+3x5+･･･


実際に展開してみるとすぐ気づきます。 それぞれの項xnの係数は、A(n)になっています。つまり、
F(x)=1+A(1)･x+A(2)･x2+A(3)･x3+A(4)･x4+ A(5)･x5･･･

展開したときの係数を調べます。
定数項はすべてのかっこから１を選んできたときだけですから１
xの１次の項は、最初のかっこのみxを選び、残りは１を選んだときのみで１
xの２次の項は、２番目のかっこのみx2を選び、 残りは１を選んだときのみで１
xの３次の項は、３番目のかっこのみx3を選び、 残りは１を選んだときと、 最初のかっこでx、２番目のかっこでx2を選んだときの２通り
xの４次の項は、４番目のかっこのみx4を選び、 残りは１を選んだときと、 最初のかっこでx、３番目のかっこでx3を選んだときの２通り
では、xの５次の項は？
異なる自然数の和で５になる組み合わせをさがすことになりますね。 5,1+4,2+3の３通りですから、x5の係数は３です。
一般にxのn次の項の係数は、 異なる自然数の和でｎになる組み合わせをさがすことになりますので、 A(n)というわけです。




　



E-mail 戻る