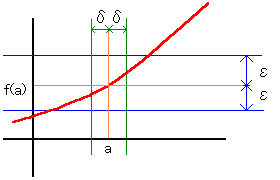
連続なところ(x=a)では、どんなに小さいεを提示されたとしても、 それに応じてδを設定することができます。
そして、 「0<|x-a|<δ ならば、|f(x)-f(a)|<ε」とはできるわけです。
Weekend Mathematics/コロキウム室/1999.4〜6/NO.63
| NO.536 | '99 6/17 | Junko | 連続の証明(10) |
確かに|x2-4|=|(x+2)(x-2)|=|x+2||x-2|ですね。ごめんなさい、勘違い!
δ<min(ε/8 ,√ε/2)としたのは、最後に|x2-4|<εとしたかったために作為的にそうしたのです。
問題はδのとり方ではなくて、δの存在です。

連続なところ(x=a)では、どんなに小さいεを提示されたとしても、
それに応じてδを設定することができます。
そして、
「0<|x-a|<δ ならば、|f(x)-f(a)|<ε」とはできるわけです。
つまり、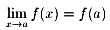 という
わけです。
という
わけです。
不連続な場所ではδが存在しないという例を挙げましょう。
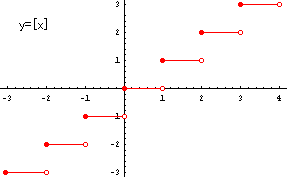
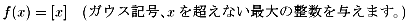
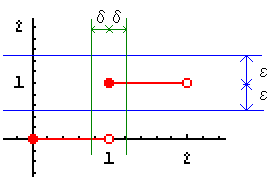
この関数はx=1において不連続です。
εは任意ですから、仮にε=1/2とします。
すうするといかなるδをもってしても、
「0<|x-1|<δ ならば、|f(x)-f(1)|<ε」とはできません。
δをどんなに小さくとったとしても、区間(1-δ,1+δ)の属するxに対するf(x)をすべて
(f(1)-ε,f(1)+ε)=(1/2,3/2)に納めることはできないからです。
具体的には、区間(1-δ,1+δ)の属するx=1-δ/2とすると、
これに対するf(x)=0ですから・・・。
つまり、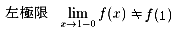 です。
です。

| NO.537 | '99 6/18 | 水の流れ | 本を棚に入れる問題(3) |
太郎さんは作業机の下にいっぱいの本があります。
一度、整理して本棚に入れたいと思っています。
入れ方にもいろいろな場合があることに太郎さんは気がつきました。
<1> 本でみると、異なる本なのか、見分けのつかない本なのかが問題になります。
<2> 本棚においても同じことで、異なる棚か、同じ棚かを考えなければなりません。
これで、この組み合わせによって、4つの場合に分かれます。まだあります。
<3>どの本棚にも必ず本を入れて空がないように入れるか、それとも本をいれない棚を
許すかにもよります。
結局8つの場合を考えて、整理することにしました。
前回(NO.531)の続きになります。
問題5:5冊の異なる本を、3個の同じ棚に入れる方法は何通りでしょうか?
ただし、空の本棚があってはいけないとする。
問題E:一般に、m冊の異なる本を、n個の同じ棚に入れる方法は何通りでしょうか?
ただし、空の本棚があってはいけないとし、m≧nとする。
問題6:5冊の異なる本を、3個の同じ棚に入れる方法は何通りでしょうか?
ただし、空の本棚があっても良いとする。
問題F: 一般に、m冊の異なる本を、n個の同じ棚に入れる方法は何通りでしょうか?
ただし、空の本棚があっても良いとし、m≧nとする。
ここからは、本も棚も区別しない場合である。
本を区別しないと、その冊数だけが問題になってくる。
したがって、この入れ方は自然数をいくつかの整数に分割することと同じになります。
問題7:m冊の同じ本を、前に入れた冊数を越えないようにして、上の棚から順に入れていく方法は何通りでしょうか?
まず、m=1,2,3,4,5,6のときを考えてください。
問題G:m冊の同じ本を、前に入れた冊数を越えないようにして、
上の棚から順に入れていく方法をS(m)とし、棚の数をkとしたとき、
その入れ方をT(m,k)とします。ただし、m≧kとする。
次の設問に答えてください。
<1> T(m,m),T(m,m―1),T(m,1)の値を求めよ。
<2> T(m,2)の値をmが奇数、偶数によって場合分けして、答えてください。
ここからは、次の等式が成り立つことを証明してください。
<3> k>m/2のとき、T(m,k)=T(m−1,k−1)
<4> k≦m/2のとき、T(m,k)=T(m−1,k−1)+T(m−k,k)
<5> k≧m/2のとき、T(m,k)=S(m−k)
<6> 特に、S(m)=T(2m,m)
太郎さんは、これらの関係を使って、S(5)、S(6)、S(7)を求めたくなりました。
皆さんの一度、確かめてください。
これで、やっと無事にいろいろな入れ方で本を整理することができました。
[問題Gについての参考文献:数学ランド・おもしろ探検(寺田文行監修):森北出版]

| NO.538 | '99 6/19 | 水の流れ | オイラーの「無限解析入門(1)」(15) |
リ−マンのゼ−タ関数は、積分によっても次のように表現できます。
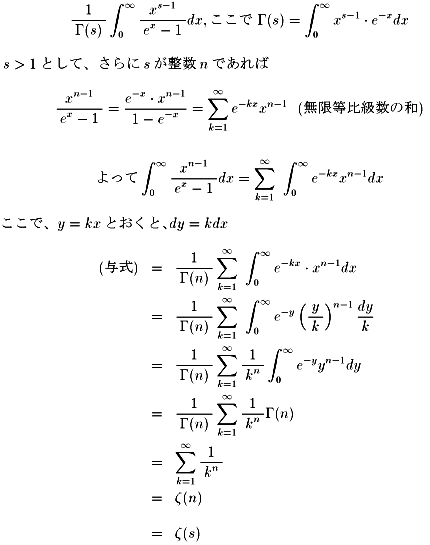
「素数の不思議:好田順治著(現代数学社)」に載っていましたので、紹介します。

| NO.539 | '99 6/19 | 浜田 明巳 | サッカーのリーグ戦 (2) |
WORDのマクロを使って解いて見ました.
このような数え上げの問題はパソコンは得意です.
ただしnチームというように,チーム数が未確定の場合はお手上げです.
5チームの場合, 4 3 2 1 0, 4 3 1 1 1,
4 2 2 2 0, 4 2 2 1 1, 3 3 3 1 0,
3 3 2 2 0, 3 3 2 1 1, 3 2 2 2 1, 2 2 2 2 2 の9通りあります.
この例えば 4 3 2 1 0 というのは,
4勝,3勝1敗,2勝2敗,1勝3敗,4敗の順位となるという意味です.
5チームの場合のプログラムを以下に示します.
それ以外のチーム数の場合も同様なプログラムです.
Sub soccer5()
Dim w(4), kosuu, j01, j02, j03, j04, j12, j13, j14, j23, j24, j34, j1, j2, j, onaji, dummy As Integer
Dim win, kekka(100), dummy2 As String
kosuu = 0
Selection.TypeText Text:="5チームの場合"
Selection.TypeParagraph
For j01 = 0 To 1: For j02 = 0 To 1: For j03 = 0 To 1: For j04 = 0 To 1
For j12 = 0 To 1: For j13 = 0 To 1: For j14 = 0 To 1
For j23 = 0 To 1: For j24 = 0 To 1: For j34 = 0 To 1
w(0) = j01 + j02 + j03 + j04
w(1) = (1 - j01) + j12 + j13 + j14
w(2) = (1 - j02) + (1 - j12) + j23 + j24
w(3) = (1 - j03) + (1 - j13) + (1 - j23) + j34
w(4) = (1 - j04) + (1 - j14) + (1 - j24) + (1 - j34)
For j1 = 0 To 3: For j2 = j1 + 1 To 4
If w(j1) < w(j2) Then
dummy = w(j1): w(j1) = w(j2): w(j2) = dummy
End If
Next: Next
win = ""
For j = 0 To 4: win = win + Str$(w(j)): Next
j = 0: onaji = 0
While j < kosuu And onaji = 0
j = j + 1: onaji = -(win = kekka(j))
Wend
If onaji = 0 Then kosuu = kosuu + 1: kekka(kosuu) = win
Next: Next: Next: Next: Next: Next: Next: Next: Next: Next
For j1 = 1 To kosuu - 1: For j2 = j1 + 1 To kosuu
If kekka(j1) < kekka(j2) Then
dummy2 = kekka(j1): kekka(j1) = kekka(j2): kekka(j2) = dummy2
End If
Next: Next
For j = 1 To kosuu
Selection.TypeText Text:=Str$(j) + "番目 " + kekka(j)
Selection.TypeParagraph
Next
Selection.TypeParagraph
End Sub
3チームの場合
| 1番目 | 2 1 0 |
| 2番目 | 1 1 1 |
4チームの場合
| 1番目 | 3 2 1 0 | 2番目 | 3 1 1 1 |
| 3番目 | 2 2 2 0 | 4番目 | 2 2 1 1 |
5チームの場合
| 1番目 | 4 3 2 1 0 | 2番目 | 4 3 1 1 1 |
| 3番目 | 4 2 2 2 0 | 4番目 | 4 2 2 1 1 |
| 5番目 | 3 3 3 1 0 | 6番目 | 3 3 2 2 0 |
| 7番目 | 3 3 2 1 1 | 8番目 | 3 2 2 2 1 |
| 9番目 | 2 2 2 2 2 |
6チームの場合
| 1番目 | 5 4 3 2 1 0 | 2番目 | 5 4 3 1 1 1 | 3番目 | 5 4 2 2 2 0 | 4番目 | 5 4 2 2 1 1 |
| 5番目 | 5 3 3 3 1 0 | 6番目 | 5 3 3 2 2 0 | 7番目 | 5 3 3 2 1 1 | 8番目 | 5 3 2 2 2 1 |
| 9番目 | 5 2 2 2 2 2 | 10番目 | 4 4 4 2 1 0 | 11番目 | 4 4 4 1 1 1 | 12番目 | 4 4 3 3 1 0 |
| 13番目 | 4 4 3 2 2 0 | 14番目 | 4 4 3 2 1 1 | 15番目 | 4 4 2 2 2 1 | 16番目 | 4 3 3 3 2 0 |
| 17番目 | 4 3 3 3 1 1 | 18番目 | 4 3 3 2 2 1 | 19番目 | 4 3 2 2 2 2 | 20番目 | 3 3 3 3 3 0 |
| 21番目 | 3 3 3 3 2 1 | 22番目 | 3 3 3 2 2 2 |
7チームの場合
| 1番目 | 6 5 4 3 2 1 0 | 2番目 | 6 5 4 3 1 1 1 | 3番目 | 6 5 4 2 2 2 0 | 4番目 | 6 5 4 2 2 1 1 |
| 5番目 | 6 5 3 3 3 1 0 | 6番目 | 6 5 3 3 2 2 0 | 7番目 | 6 5 3 3 2 1 1 | 8番目 | 6 5 3 2 2 2 1 |
| 9番目 | 6 5 2 2 2 2 2 | 10番目 | 6 4 4 4 2 1 0 | 11番目 | 6 4 4 4 1 1 1 | 12番目 | 6 4 4 3 3 1 0 |
| 13番目 | 6 4 4 3 2 2 0 | 14番目 | 6 4 4 3 2 1 1 | 15番目 | 6 4 4 2 2 2 1 | 16番目 | 6 4 3 3 3 2 0 |
| 17番目 | 6 4 3 3 3 1 1 | 18番目 | 6 4 3 3 2 2 1 | 19番目 | 6 4 3 2 2 2 2 | 20番目 | 6 3 3 3 3 3 0 |
| 21番目 | 6 3 3 3 3 2 1 | 22番目 | 6 3 3 3 2 2 2 | 23番目 | 5 5 5 3 2 1 0 | 24番目 | 5 5 5 3 1 1 1 |
| 25番目 | 5 5 5 2 2 2 0 | 26番目 | 5 5 5 2 2 1 1 | 27番目 | 5 5 4 4 2 1 0 | 28番目 | 5 5 4 4 1 1 1 |
| 29番目 | 5 5 4 3 3 1 0 | 30番目 | 5 5 4 3 2 2 0 | 31番目 | 5 5 4 3 2 1 1 | 32番目 | 5 5 4 2 2 2 1 |
| 33番目 | 5 5 3 3 3 2 0 | 34番目 | 5 5 3 3 3 1 1 | 35番目 | 5 5 3 3 2 2 1 | 36番目 | 5 5 3 2 2 2 2 |
| 37番目 | 5 4 4 4 3 1 0 | 38番目 | 5 4 4 4 2 2 0 | 39番目 | 5 4 4 4 2 1 1 | 40番目 | 5 4 4 3 3 2 0 |
| 41番目 | 5 4 4 3 3 1 1 | 42番目 | 5 4 4 3 2 2 1 | 43番目 | 5 4 4 2 2 2 2 | 44番目 | 5 4 3 3 3 3 0 |
| 45番目 | 5 4 3 3 3 2 1 | 46番目 | 5 4 3 3 2 2 2 | 47番目 | 5 3 3 3 3 3 1 | 48番目 | 5 3 3 3 3 2 2 |
| 49番目 | 4 4 4 4 4 1 0 | 50番目 | 4 4 4 4 3 2 0 | 51番目 | 4 4 4 4 3 1 1 | 52番目 | 4 4 4 4 2 2 1 |
| 53番目 | 4 4 4 3 3 3 0 | 54番目 | 4 4 4 3 3 2 1 | 55番目 | 4 4 4 3 2 2 2 | 56番目 | 4 4 3 3 3 3 1 |
| 57番目 | 4 4 3 3 3 2 2 | 58番目 | 4 3 3 3 3 3 2 | 59番目 | 3 3 3 3 3 3 3 |

| NO.540 | '99 6/21 | 水の流れ | オイラーの「無限解析入門(1)」(16) |
オイラーの「無限解析入門(1)」第8夜の始まり、始まり。
自然数全体の和はオイラーが1749年にゼーター関数を用いて、
奇妙な計算結果を導きました。
1+2+3+4+・・・=−1/12
そして、自然数の積はリーマンが1859年にゼーター関数を用いて、
次のような奇妙な計算結果を導きました。
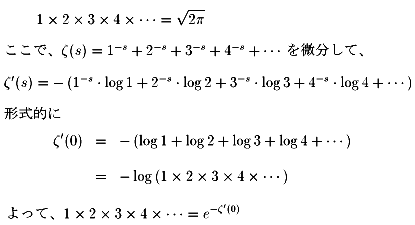
そこで、今夜の宿題です。
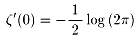 を示してください。
を示してください。

| NO.541 | '99 6/22 | Junko | 本を棚に入れる問題(4) |
5.NO.532の2の150通りを考えます。
これは3つある本棚の区別があるわけです。
ですから、5冊の本をA,B,C,D,Eとすれば、
[(A,B),(C,D),(E)]と[(C,D),(A,B),(E)]は違うものと考えていたわけです。
しかしここでは、本棚に区別がないのですから両者は同じものとみなします。
こういったものが、3!=6通りずつあります。
従って、150/3!=25
E.これを一般化すると、B(n,k)/k!
6.全部で35=243通りある中で、
1ヶ所に集中してしまう3通りを除いた240通りについては、5番の問題と同様に3!=6通りずつ同じものがある
わけですから、240/6=40
1ヶ所に集中してしまう3通りについては、空の棚が2つ(つまり同じものが2つ)ですから同等をみなせるもの
が3!/2=3通りあります。3/3=1
[(A,B,C,D,E),( ),( )]と[( ),(A,B,C,D,E),( )]と[( ),( ),(A,B,C,D,E)]
両者をたして、40+1=41
F.一般に、m冊の異なる本を、n個の同じ棚に入れる方法がF(m,n)通りあるとします。
ただし、空の本棚があっても良いとし、m≧nです。
本棚が1つしかないわけですから、F(m,1)=1
本棚が2つとすると、2!=2通りずつ同等なものがありますから、
F(m,2)=2m/2!=2m−1
本棚が3つの場合は、空の棚が0,1の場合は3!=6通りずつ、
空の棚が2の場合は、3!/2=3通りずつ同等なものがあります。
m冊の異なる本を、n個の異なる棚に入れる方法を、B(m,n)通りとすれば、
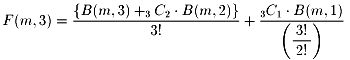
一般的には、空の棚の個数が何個あるかによって、同等と見なせる数が違うので、
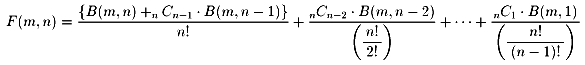
でも、あまりきれいな式ではありませんね。もっとすっきりさせたいのですが・・・。
7.棚に入れる本の冊数を(a,b,c,・・・)で表すことにします。
ただし、a≧b≧c≧・・・≧1とします。
G.<1>
<2>
T(m,2)をmの偶奇に分けて考えます。
本棚は2つしかありませんから、
<3>
空の棚は認めないので、最後の棚の冊数は0ではありません。
k>m/2より、2冊ということもあり得ません。
従って、1冊ということになります。
つまり、残り(m−1)冊の本を(k−1)個の棚に入れればいいことになります。
従って、T(m,k)=T(m−1,k−1)
<4>
k≦m/2のとき、T(m,k)=T(m−1,k−1)+T(m−k,k)
k≦m/2より最後の棚に入る本の冊数は2冊以上の可能性もあります。
そこで、最後の棚に入る本の数が1冊の場合と、2冊以上になる場合とに分けます。
1冊の場合は、残り(m−1)冊の本を(k−1)個の棚に入れればいいことになります。
従って、T(m−1,k−1)通り。
2冊以上の場合。
一番最後の棚が2冊以上ですから、すべての棚が2冊以上ということになります。
そこで、最初に1冊ずつ入れてしまいます。
その後、残りの(m−k)冊の本の入れ方を考えます。
この時は、0冊という棚があってもいいわけです。
従って、T(m−k,k)通り。
というわけで、T(m,k)=T(m−1,k−1)+T(m−k,k)
<5>
k≧m/2のとき、T(m,k)=S(m−k)
すべての棚に本を1冊づついれてしまいます。
その後、残りの(m−k)冊の本の入れ方を考えます。
この時は、0冊という棚があってもいいわけです。
<6>
<5>において、m≧m/2だから、
T(2m,m)=S(2m−m)=S(m)
| S(5) | =T(10,5) |
| =T(9,4)+T(5,5) | |
| =T(8,3)+T(5,4)+1 | |
| =T(7,2)+T(5,3)+1+1 | |
| =T(6,1)+T(5,2)+T(4,2)+2 | |
| =1+T(4,1)+T(3,2)+T(3,1)+T(2,2)+2 | |
| =1+1+1+1+1+2 | |
| =7 |

| NO.542 | '99 6/23 | 水の流れ | オイラーの「無限解析入門(1)」(17) |
オイラーの「無限解析入門(1)」第9夜の始まり、始まり。
今夜は「数学の宇宙(現代数学者:中村由子訳)」を読んで、
多くの引用をさせてもらいながら、お話をします。
オイラーは1740年の秋に、フランスの数学者フィリップ・ノードから、
「自然数を異なる自然数の和として表わす方法がいくるあるか?」
という手紙を受け取りました。これが、オイラーの興味を引きました。
数日後、彼は「ここ数週間苦しめられた視力の低下のせいで返事の遅れた」
ことを詫びる手紙を添えて解答を送りました。
解答の紹介は後にしまして、少し説明します。
例えば、n=6のとき、異なる自然数の和として、次の4通りがあります。
6,5+1、4+2,3+2+1 です。
6を構成している数字は1回だけしか使えません。
だから、異なっている数字なら、数字はいくつ使ってもよいです。
ここで、ある自然数nを異なる自然数の和で表わす方法をA(n)とします。
つまり、A(6)=4 です。
次に、6を構成している数字が奇数だけになっている方法を考えて見ます。
5+1,3+3,3+1+1+1,1+1+1+1+1
の4通りです。奇数という制限はありますが、
同じ数字を繰り返して使ってもよいです。
ある自然数を奇数の和で表す方法をB(n)とすれば、
B(6)=4となります。
皆さん、A(6)=4 、B(6)=4 が偶然に一致したかどうか、
これから、2,3調べてください。
これが今夜の宿題です。
n=7,8,・・・を調べてください。

| NO.543 | '99 6/26 | Junko | オイラーの「無限解析入門(1)」(18) |

| NO.544 | '99 6/27 | 水の流れ | オイラーの「無限解析入門(1)」(19) |
オイラーの「無限解析入門(1)」第10夜の始まり、始まり。
昨晩、ある自然数nを異なる自然数の和で表わす方法をA(n)として、
2,3調べてくださいと、言って床につきましたが、
この数列はいちいち計算しなければならないのでしょうか?
いえいえ、当然ある関数の係数として表れてきます。これが、母関数です。
そこで、皆さん、今夜の宿題です。
次の関数を展開してくださいね。
当然係数に注目ください。
そして、この係数がどうして、数列{A(n)}なのかも考えてください。
F(x)=(1+x)(1+x2)(1+x3)(1+x4)・・・・・・

| NO.545 | '99 6/27 | 水の流れ | 同窓会 |
太郎さんは昨日、n人(n≧2)同窓会に参加してきました。
もちろん、この同窓会に参加した各人は、参加者の中で、
何人かの友人を持っているいるとします。
そこで、各人に参加者の中で何人の友人がいるか尋ねます。
このとき、友人数が同じであるような人が少なくとも2人いることを
示してください。

 E-mail
E-mail
 戻る
戻る