
Weekend Mathematics/コロキウム室/1999.4〜6/NO.60
| NO.505 | '99 6/1 | Junko | 「数学の宇宙」(1) |
ゼ−タ−関数物語を書くにあたって
「水の流れ」さんが引用したという、
W・ダンハム著「数学の知性」(現代数学社 \3500)
を最近読んでみました。
天才数学者の業績はもちろんですが、その人間性がかかれていて
とてもおもしろい本でした。
「天才と定理でたどる数学史」というサブタイトルがついている通り、
数学が発展してきた歴史もたどることができます。
数学を専門にしていない人にこそ読んでほしいと思います。
そうすることで、数学の持つ魅力をわかってもらえるのではないかと思います。
同じ著者にもう1冊著作があるということで、今それを読んでいます。
「数学の宇宙」(現代数学者 \3500)です。
「Arithemetic(数論)」から始まって、「Z(Z)」までアルファベット順に
いろいろな話がでてきます。
もちろん数学の話ではありますが、それにまつわるエピソ−ドやetc.がなかなか
おもしろいのです。
基本的にはどこから読んでもいいわけで、
私はやっぱり「Prime Number Theorem(素数定理)」から読みました。

| NO.506 | '99 6/1 | 水の流れ | オイラーの「無限解析入門(1)」(13) |
オイラーの「無限解析入門(1)」の第7夜の始まり、始まり。
前夜、ガンマ関数Γ(s)の話をしましたね。
もう一度、書いておきます。
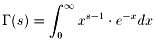
を言います。
さて、いきなりですが、今夜の宿題です。
次の関数が、ゼーター関数ζ(s)の積分における表現になっていること
を示してください。
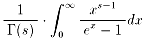
皆さん、この積分をしてみてください。今夜は短いお話でした。

| NO.507 | '99 6/1 | 水の流れ | 高貴な未解決問題(1) |
コロキウム室は人間的歓喜を呼び起こす何かがあります。
この6月1日で3年目に入り、おめでとうございます。
さて、<未だ見ぬ偉大な数学者たち>へ、
これから、数の不思議(神秘)を研究するために、
あなたは青春をかけてみてください。
現在までに、先代の数学者が青春をかけて、没頭した美しい未解決な
問題を順に紹介します。
第1話:「素数の数列の一般項」と「メルセンヌ素数」
2,3,5,7,11,13,17,・・・
<参考文献:1.新数学辞典(大阪書店)
2.素数の不思議:好田順治著(現代数学社)>

| NO.508 | '99 6/2 | 数楽者 | オレンジの問題・その後(1) |
オレンジの問題について
4人で分ける場合、8で割った余りで場合分けすると
オレンジを半分にしなくても分けることができます。
4人の分け前を(a、b、c、d)で表すことにします。
分け方の例1
| 余り | 分け前 |
|---|---|
| 1 | (1,0,0,0) |
| 2 | (1,1,0,0) |
| 3 | (1,1,1,0) |
| 4 | (1,1,1,1) |
| 5 | (1,1,1,2) |
| 6 | (1,1,2,2) |
| 7 | (1,2,2,2) |
このようにすれば、各人がもらうオレンジの期待数は同じになります。
なお、以下のようにすると、個数ごとのもらう確率も同じになります。
分け方の例2
| 余り | 分け前 |
|---|---|
| 1 | (1,0,0,0) |
| 2 | (0,2,0,0) |
| 3 | (0,0,2,1) |
| 4 | (1,1,1,1) |
| 5 | (2,1,1,1) |
| 6 | (1,1,2,2) |
| 7 | (2,2,1,2) |

| NO.509 | '99 6/3 | 月の光 | オイラーの「無限解析入門(1)」(14) |


| NO.510 | '99 6/3 | Junko | オレンジの問題・その後(2) |
オレンジの問題についての
「数楽者」さんのコメント(NO.508)を読んで、びっくり!
4人で分ければ、剰余の可能性は0,1,2,3の4とおりと考えるのが当然ですよね。
しかしながら、追加分配するオレンジ期待値を平等にし、しかもオレンジを切らずにすむように、
あえて「8」(もちろん4の2倍)の剰余で考えるとは・・・!!!
発想の転換とはこのことですね。
余りが4個以上のときに、それぞれ最低1個を保証するような分配を考えれば、
結果も同じことですしね。

| NO.511 | '99 6/3 | 月の光 | 連続の証明(1) |
昨日友達にこんな問題を聞かれました。
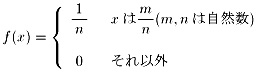
とする。
xが無理数のとき、f(x)が連続であることを証明せよ。
僕はこう考えました。

どうしたらいいでしょうか。
追加
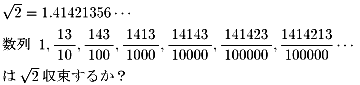

| NO.512 | '99 6/3 | 水の流れ | バーレーボールの得点 |
太郎さんが勤務している学校で先日、バーレーボール大会がありました。 6人制バレーボールでは、毎回の勝負はサーブ権を持ったチームのサーブで 始まり、ここで勝った方が次回のサーブ権を得る。 またこのとき勝った方がサーブ権を持っていた ならば1点を得点するが、サーブ権を持っていなかったらば、 単にサーブ権を獲得するだけで得点はしない。
第1試合、両チーム間の各回の勝率は、
サーブ側であるか否かに関係なくAが4割、Bは6割であるとする。
Aのサーブで試合が開始されたとして、次の問に答えよ。
問題1.先に1点を得点するのがAである確率を求めよ。
問題2.先に2点を得点するのがAである確率を求めよ。
第2試合、両チーム間の各回の勝率は、サーブ側であるか否かに関係なく
Aが5割、Bは5割であるとする。
Aのサーブで試合が開始されたとして、次の問に答えよ。
問題3.先に1点を得点するのがAである確率を求めよ。
問題4.先に2点を得点するのがAである確率を求めよ。
問題5.先に3点を得点するのがAである確率を求めよ。
太郎さんも童心にかえって、バレーボールを楽しんでいましたが、
サーブ権の移動だけで、なかなか得点できないことがあることが、
気になってしかたがありません。
皆さんも、考えてください。

| NO.513 | '99 6/4 | Weadore | タイル敷き(2) |
NO.463タイルの問題
の積分を用いた解答です。
xy平面上の第1象限のカドに(原点の直交している2線に重なるように)
置いた長方形
R = {(x, y) : 0≦x≦b, 0≦y≦d}
が、一辺の長さが整数であるようなn個の長方形タイルRi, i = 1,2,...,nで
敷き詰められていたとする。
ここで、
Ri = {(x, y) : ai≦x≦bi,
ci≦y≦di}
とすると、(bi - ai)か(di - ci)
のいずれか一方は整数である。
ここで、R上でのsin(2πx), sin(2πy)の2重積分を考える。
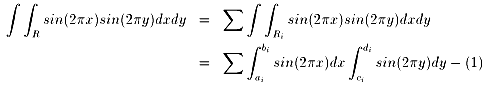
また、、(bi - ai)か(di - ci)
のいずれか一方は整数であるので、
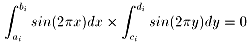
また、それぞれのiでも0である。すなわち、(1)の右辺では結果
0 + 0 + 0 +....となり、0である。
よって、(1)は
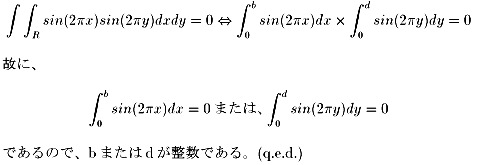
であるので、bまたはdが整数である。(q.e.d.)
この積分の方の解答は、sinを使うところが見事ですよね。感動です。

| NO.514 | '99 6/4 | Junko | 連続の証明(2) |
この問題はきっちりいかないといけないかなと思います。
まずは、連続性の定義から
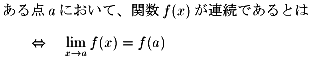
逆に連続でない例をあげましょう。
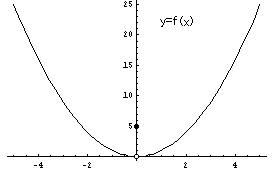
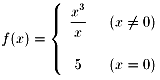
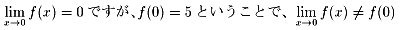
つまり x=0で不連続です。
もう1つ例を上げます。
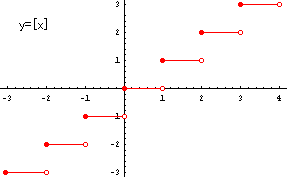
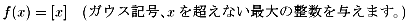
これは、すべての整数値で不連続です。
例えば、x=1において連続でないことを示します。

ですから、f(1)=1と一致するかどうか議論する以前の問題です。
(厳密にいえば、左極限と右極限が一致して初めて極限の存在がいえることになります。)
右極限と関数値は一致していますけれどね・・・それだけではだめなのです。
この続きはまた次回・・・。

| NO.515 | '99 6/4 | Idaho Potato | 連続の証明(3) |
あっさり答を披露してしまうとおもしろくないので、 少々遊んで(失礼!)みます。
月の光さんがNo.511に示した「連続性の証明」は、 次の命題が成り立つことを前提としています。
それなら、No.511の証明を次のように修正すればよいことになります。
a を無理数とする。 Sn = a - 1/10n, Tn = a + 1/10n とすると、 数列 { Sn }, { Tn } は、 それぞれ単調増大、単調減少で、いずれも a に収束する。 しかも、すべての n について、 Sn, Tn は無理数なので、 f(Sn) = f(Tn) = 0 = f(a) である。 したがって、命題Aにより、関数 f は x = a で連続となる。それところが、もし命題Aが正しいならば、 上の証明と全く同じ考え方で、次の命題を証明することができます。
何かおかしいと思いませんか?
ちょっと考えればすぐわかることですが、実は、
命題Bの関数 f は、
「いたる所『不連続』な関数」の典型的な例なのです(ディリクレ関数といいます)。
そういうわけで、 月の光さんの証明が正しくないことの本当の理由は、 もっと根本的なところにあるのです。 「m/n は既約分数」云々というのは、細かい技術的な問題であって、 本質的ではありません。
実は、
No.511の関数の(無理数の点における)連続性を証明するには、
「関数が連続であるとはどういうことか」という、
大学教養課程の解析学の基礎知識が本質的に必要になるのです。

 E-mail
E-mail
 戻る
戻る