
Weekend Mathematics乛栤戣乛栤戣29
俀俋丏僆儗儞僕偺栤戣

崱擭傕僗儈僗巵偺傕偲傊丄僇儕僼僅儖僯傾偺桭恖偐傜偨偔偝傫偺僆儗儞僕偑憲傜傟偰偒傑偟偨丅
懅巕偺僕儑儞孨丄柡偺儊傾儕亅偝傫丄僗儈僗巵偲丄俁恖偱暯摍偵暘偗偨偄偲巚偄傑偡丅
偱傕丄僆儗儞僕偺屄悢偑俁偱妱傝愗傟傞偲偼尷傝傑偣傫丅偳偆偟偨傜偄偄偱偟傚偆丅
巚埬偺枛丄僗儈僗巵偼柤埬傪巚偄偮偒傑偟偨丅
俁恖偱暘偗傞偺偱偡偐傜丄偪傚偆偳暘偗傜傟傞偐丄
侾屄梋傞偐丄俀屄梋傞偐偺偄偢傟偐偟偐偁傝傑偣傫丅
偟偐傕丄偦偺妋棪偼摍偟偄偲峫偊偰傛偄偱偟傚偆丅
傕偟侾屄梋偭偨傜丄僗儈僗巵偑偦傟傪傕傜偆偙偲偵偟傑偡丅
偦偺妋棪偼侾乛俁偱偡丅
傕偟俀屄梋偭偨傜丄僕儑儞孨偲儊傾儕亅偝傫偑侾屄偢偮傕傜偆偙偲偵偟傑偡丅
偙偺妋棪傕侾乛俁偱偡丅
偙偆偟偰慡懱偲偟偰偼丄侾屄梋暘偵傕傜偊傞妋棪偑丄俁恖偲傕暯摍偵側傞偲偄偆傢偗偱偡両
偝偰偦偙傊丄傂傚偭偙傝偍偽偁偪傖傫偑傗偭偰偒傑偟偨丅
係恖偱岞暯偵暘偗傞丄摨偠傛偆側曽朄偑偁傞偱偟傚偆偐丠
乽敿暘偙乿傪偟偰傛偗傟偽偳偆偱偟傚偆丠
傂傜傔偒巚峫丂Part嘨
I.C.僼儕僢僇亅曇
擔宱僒僀僄儞僗幮
乮儁儞僱亅儉丗偐偵乯
係恖偱岞暯偵暘偗傞摨偠傛偆側曽朄偼偁傝傑偣傫丅
偨偩偟丄敿暘偙偟偰傛偗傟偽係恖偱岞暯偵暘偗傞偙偲偑偱偒傑偡丅
ABCD偺係恖偵偍偄偰丄僆儗儞僕偑侾屄梋偭偨傜A偲俛偱敿暘偙偟偰
僆儗儞僕傪傕傜偄傑偡丅俀屄梋偭偨傜敿暘偙偟偰ABCD偺係恖偱傕傜
偄傑偡丅俁屄梋偭偨傜A偲B偱敿暘偙偟偨僆儗儞僕傪傕傜偄丄C偲D偼
僆儗儞僕傪侾屄偢偮傕傜偄傑偡丅
偙偺傛偆偵偡傞偲慡懱偲偟偰偼丄侾屄敿梋暘偵傕傜偊傞妋棪偑係恖
偲傕暯摍偵側傞偲巚偄傑偡丅
乮儁儞僱亅儉丗傒傗乯
侾丏係恖偱暘偗傞偙偲偼弌棃側偄丅
俀丏敿暘偙偡傞応崌
偦傟偧傟偵値屄偯偮攝傝丄梋傝傪埲壓偺昞偺傛偆偵偟傑偡丅
| 梋傝侽 | 梋傝侾 | 梋傝俀 | 梋傝俁 | |
|---|---|---|---|---|
| 堦榊 | 侽 | 侾乛俀 | 侾乛俀 | 侾乛俀 |
| 師榊 | 侽 | 侽 | 俁乛俀 | 侽 |
| 嶰榊 | 侽 | 侾乛俀 | 侽 | 侾 |
| 巐榊 | 侽 | 侽 | 侽 | 俁乛俀 |
幹懌
偙偺攝傝曽偼暯摍偲偼尵偄偒傟側偄偲偄偆寢榑傪柍棟傗傝摫偄偰傒傑偡丅
慡堳丄僆儗儞僕傪値屄傕傜偭偨偲偒偺婐偟偝傪
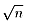 偲偟傑偡丅
偲偟傑偡丅
乮拲)
偦傟偧傟偺婐偟偝偺婜懸抣偼
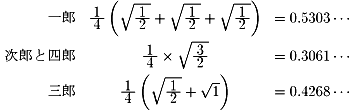
傛偭偰婐偟偝偺婜懸抣偼堦榊偑堦斣崅偄丅
乮拲乯
側偤値屄傕傜偭偨偲偒偺婐偟偝傪値偱偼側偔
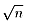 偵偟偨偐偲偄偆偲
椺偊偽僆儗儞僕俀屄傕傜偭偨偲偒偼婐偟偄偱偡偹丅
偟偐偟俋俉屄傕傜偭偨偲偒偲侾侽侽屄傕傜偭偨偲偒偺婐偟偝偼摨偠偱偡偹丅
偦傟偱婐偟偝傪儖乕僩偱昞偟傑偟偨丅
偩偐傜偙偺椺偱傕丄傑偢侾侽屄偯偮攝傝梋傝傪忋偺傛偆偵
暘偗偨偲偟偨傜婐偟偝偺婜懸抣偼傎偲傫偳摨偠偵側傞偼偢偱偡丅
偵偟偨偐偲偄偆偲
椺偊偽僆儗儞僕俀屄傕傜偭偨偲偒偼婐偟偄偱偡偹丅
偟偐偟俋俉屄傕傜偭偨偲偒偲侾侽侽屄傕傜偭偨偲偒偺婐偟偝偼摨偠偱偡偹丅
偦傟偱婐偟偝傪儖乕僩偱昞偟傑偟偨丅
偩偐傜偙偺椺偱傕丄傑偢侾侽屄偯偮攝傝梋傝傪忋偺傛偆偵
暘偗偨偲偟偨傜婐偟偝偺婜懸抣偼傎偲傫偳摨偠偵側傞偼偢偱偡丅
侾侽屄攝偭偨屻偵梋傝傪忋偺昞偺傛偆偵暘偗傞偲
乮僆儗儞僕偑係侽偐傜係俁偺偲偒乯
| 梋傝侽 | 梋傝侾 | 梋傝俀 | 梋傝俁 | |
|---|---|---|---|---|
| 堦榊 | 侾侽 | 21乛俀 | 21乛俀 | 21乛俀 |
| 師榊 | 侾侽 | 侾侽 | 23乛俀 | 侾侽 |
| 嶰榊 | 侾侽 | 21乛俀 | 侾侽 | 侾侾 |
| 巐榊 | 侾侽 | 侾侽 | 侾侽 | 23乛俀 |
| 堦榊 | 3.2209 |
| 師榊偲巐榊丂丂 | 3.2195 |
| 嶰榊 | 3.2204 |
乮儁儞僱亅儉丗Weadore乯
嵟弶偵偁傞僆儗儞僕偺悢傪mod8偱応崌暘偗偟偰峫偊傑偡丅
0,4偺応崌偼丄(A,B,C,D)偵(1,1,1,1)丄
1偺応崌偼丄(A,B,C,D)偵(0,1,0,0)丄
2偺応崌偼丄(A,B,C,D)偵(0,0,2,0)丄
3偺応崌偼丄(A,B,C,D)偵(0,0,0,3)丄
5,6,7偺応崌偼丄傑偢丄(A,B,C,D)偵(1,1,1,1)偲丄傢偗傞丅偦偺屻丄
5偺応崌偼丄(A,B,C,D)偵(1,0,0,0)丄
6偺応崌偼丄(A,B,C,D)偵(0,2,0,0)丄
7偺応崌偼丄(A,B,C,D)偵(0,0,3,0)丄偱暘偗傑偡丅
偙偆偡傟偽丄僆儗儞僕傪傕傜偊傞悢偺婜懸抣偼摍偟偔側傝傑偡丅
乮佹廲偵悢傪懌偟偰傒傟偽偡偖暘偐傞丅乯
偨偩丄偙偺忋偺椺偩偲丄偁傑傝暯摍偵尒偊側偄偺偱丄
屻偼丄懡彮尒偨栚忋偺栤戣偱応崌暘偗偺偲偙傠偱丄
堦恖堦屄偢偮搉偣偽椙偄偲巚偄傑偡丅
偙偙偱丄1,2,3偲5,6,7傪偆傑偔懳徧揑偵偡傞偲偆傑偔峴偒傑偡丅
敿暘偙傪偟偰OK偺応崌偼丄mod4偱応崌暘偗偟偰丄
0偺応崌偼丄(A,B,C,D)偵(1,1,1,1)丄
1偺応崌偼丄(A,B,C,D)偵(1,0,0,0)丄
3偺応崌偼丄(A,B,C,D)偵(0,1,1,1)丄
2偺応崌偼丄(A,B,C,D)偵(0.5,0.5,0.5,0.5)
偭偲暘偗傟偽丄暯摍偵攝傟傞丅
乮儁儞僱亅儉丗昹揷丂柧枻乯
丂俙丆俛丆俠偺俁恖偵僆儗儞僕傪暘偗傞偲偟丆師偺昞偺傛偆偵傑偲傔傑偡丏
| 梋傝 | 俙 | 俛 | 俠 |
|---|---|---|---|
| 侽 | 侽 | 侽 | 侽 |
| 侾 | 侾 | 侽 | 侽 |
| 俀 | 侽 | 侾 | 侾 |
| 梋傝 | 俙 | 俛 | 俠 | 俢 |
|---|---|---|---|---|
| 侽 | 侽 | 侽 | 侽 | 侽 |
| 侾 | 侾 | 侽 | 侽 | 侽 |
| 俀 | 侽 | 侾 | 侾 | 侽 |
| 俁 | 丠 | 丠 | 丠 | 丠 |
| 梋傝 | 俙 | 俛 | 俠 | 俢 |
|---|---|---|---|---|
| 侽 | 侽 | 侽 | 侽 | 侽 |
| 侾 | 1/2 | 1/2 | 侽 | 侽 |
| 俀 | 1/2 | 1/2 | 1/2 | 1/2 |
| 俁 | 1/2 | 1/2 | 侾 | 侾 |
乮儁儞僱亅儉丗偪傖傔乯
係恖偱岞暯偵暘偗傞偲偄偆偙偲傪丄
乽係恖偦傟偧傟偺丄梋暘偵傕傜偊傞屄悢偺婜懸抣偑摍偟偄乿偙偲偲峫偊傞丅
俁偱妱傞応崌偲摨條丄係偱妱偭偰丄梋傝偑侽丆侾丆俀丆俁偲側傞妋棪偼偡傋偰 1/4偱偁傞偲偟偰傛偄丅
偡傞偲丄係偱妱偭偰梋傞屄悢偺婜懸抣偼丄(0+1+2+3)/4 = 3/2乮屄乯
偱偁傞偐傜丄係恖偦傟偧傟偑丄
梋暘偵傕傜偊傞屄悢偺婜懸抣偑 3/8 屄偲側傞傛偆側曽朄傪峫偊傟偽傛偄丅
埲壓丄係恖偺嬫暿偼峫椂偣偢偵丄暘偗傞屄悢偺慻傒崌傢偣偩偗傪峫偊傞偙偲偵偡傞丅
係恖傪丄x , y, z, w 偲昞偡丅
係偱妱偭偨梋傝偑k屄(k=1,2,3)偱偁傞偲偒偵x偑傕傜偆屄悢傪x(k)偲昞偡丅
x(k)偼旕晧偺惍悢偱偁傞丅
x偑梋暘偵傕傜偆屄悢偺婜懸抣偑3/8偲側傞偨傔偵丄
x(1)+x(2)+x(3) = 3/2
偱側偗傟偽側傜側偄偑丄偙傟傪枮偨偡旕晧偺惍悢x(k)(k=1,2,3)偼懚嵼偟側偄丅
傛偭偰丄岞暯側暘偗曽偼偱偒側偄丅
師偵丄乽敿暘偙乿壜擻側応崌傪峫偊傞丅
忋偱掕傔偨 x(k) 傪 1/2屄傪扨埵偲偟偰昞偟偨悢丄
偡側傢偪 2x(k) 傪偁傜偨傔偰 x(k) 偲抲偔丅
x(k)偼旕晧偺惍悢丅
y(k), z(k), w(k) 傕摨條偵掕傔傞丅
奺恖偑梋暘偵傕傜偆屄悢偺婜懸抣偑偡傋偰3/8偲側傞偨傔偵丄
x(1)+x(2)+x(3)=3 丒丒丒(1)
y(1)+y(2)+y(3)=3 丒丒丒(2)
z(1)+z(2)+z(3)=3 丒丒丒(3)
w(1)+w(2)+w(3)=3 丂丒丒丒(4)
傑偨丄暥帤偺掕傔曽偐傜丄
x(1)+y(1)+z(1)+w(1)=2丂丒丒丒(5)
x(2)+y(2)+z(2)+w(2)=4 丒丒丒(6)
x(3)+y(3)+z(3)+w(3)=6 丒丒丒(7)
(1)偐傜(7)傪枮偨偡旕晧惍悢夝偑懚嵼偡傟偽岞暯側暘偗曽偑壜擻丅
x(k), y(k), z(k), w(k) 偵娭偡傞懳徧惈偐傜丄
x(3)>=y(3)>=z(3)>=w(3)偲偟偰傛偄丅
x(3)<=3偩偐傜丄(7)偐傜丄
(x(3), y(3), z(3), w(3))=(3,3,0,0), (3,2,1,0),(3,1,1,1),(2,2,2,0),(2,2,1,1,)
| [(0, 0, 3/2) | (0, 0, 3/2) | (0, 3/2 0) | (1, 1/2 ,0)] |
| [(0, 0, 3/2) | (0. 0, 3/2) | (1/2, 1, 0) | (1/2 ,1, 0)] |
| [(0, 0, 3/2) | (1/2, 0 ,1) | (1/2, 1/2, 1/2) | (0, 3/2, 0)] |
| [(0, 0, 3/2) | (1/2, 0, 1) | (0, 1, 1/2) | (1/2, 1, 0)] |
| [(0, 0, 3/2) | (0, 1/2, 1) | (1/2, 1/2, 1/2) | (1/2, 1, 0)] |
| [(0, 0, 3/2) | (0, 1/2, 1) | (1, 0, 1/2) | (0, 3/2 0)] |
| [(0, 0, 3/2) | (0, 1/2 ,1) | (0, 1, 1/2) | (1, 1/2 ,0)] |
| [(0, 0, 3/2) | (1, 0, 1/2) | (0, 1, 1/2) | (0, 1, 1/2)] |
| [(0, 0, 3/2) | (1/2, 1/2, 1/2) | (1/2, 1/2, 1/2) | (0, 1, 1/2)] |
| [(1/2, 0, 1) | (1/2, 0 ,1) | (0, 1/2, 1) | (0, 3/2, 0)] |
| [(1/2, 0, 1) | (0, 1/2, 1) | (0, 1/2, 1) | (1/2, 1, 0)] |
| [(0, 1/2, 1) | (0, 1/2, 1) | (0, 1/2, 1) | (1, 1/2, 0)] |
| [(1/2, 0, 1) | (1/2, 0, 1) | (0, 1, 1/2) | (0, 1, 1/2)] |
| [(1/2, 0, 1) | (0, 1/2, 1) | (1/2, 1/2, 1/2) | (0, 1, 1/2)] |
| [(0, 1/2, 1) | (0, 1/2, 1) | (1, 0, 1/2) | (0, 1, 1/2)] |
| [(0, 1/2, 1) | (0, 1/2, 1) | (1/2, 1/2, 1/2) | (1/2, 1/2, 1/2)] |
乮儁儞僱亅儉丗峳忛丂惔旤乯
係恖偱傢偗傞偐傜
乮儁儞僱亅儉丗偪傚傑乯
僗儈僗巵丄僕儑儞孨丄儊傾儕亅偝傫丄偍偽偁偪傖傫傪
俙丄俛丄俠丄俢偲彂偔偙偲偵偟傑偡丅
偙偺係恖偱梋偭偨僆儗儞僕傪岞暯偵暘偗傞曽朄傪乮侾乯乣乮俁乯偺弴
偵峫偊偰傒傑偟偨丅
偐偵丆傒傗丆Weadore丆昹揷丂柧枻丆偪傖傔丆峳忛丂惔旤丆偪傚傑

傕偟僆儗儞僕偑梋偭偨傜丄僆儗儞僕僕儏亅僗傪嶌偭偰奆偱堸傓丄
側傫偰摎偊偨傜搟傜傟偰偟傑偆偐側丠
偝偰係恖偱岞暯偵暘攝偱偒側偄偺偼丄乽昹揷丂柧枻乿偝傫偺偛巜揈捠傝丄
壜擻惈偺偁傞梋傝偺憤榓偑恖悢偱妱傝愗傟側偄偙偲偱愢柧偱偒傑偡丅
(侽亄侾亄俀亄俁)亐係亖俇亐係
堦斒偵俶恖偱暘攝偟傛偆偲偡傞偲丄壜擻惈偺偁傞梋傝偺憤榓
侽亄侾亄俀亄俁亄丒丒丒亄(俶亅侾)亖俶(俶亅侾)乛俀偑恖悢俶偱妱傟傞偐偳偆偐偑栤戣偵側傝傑偡丅

| 梋傝 | 俙1 | 俙2 | 丒丒丒 | 俙N/2 | 俙N/2+1 | 丒丒丒 | 俙N-1 | 俙N |
|---|---|---|---|---|---|---|---|---|
| 侾 | 仜 | 亊 | 亊 | 亊 | 亊 | 亊 | 亊 | 亊 |
| 俀 | 仜 | 仜 | 亊 | 亊 | 亊 | 亊 | 亊 | 亊 |
| 俁 | 仜 | 仜 | 仜 | 亊 | 亊 | 亊 | 亊 | 亊 |
| 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 |
| (N-1)/2 | 仜 | 仜 | 仜 | 仜 | 亊 | 亊 | 亊 | 亊 |
| (N+1)/2 | 亊 | 亊 | 亊 | 亊 | 仜 | 仜 | 仜 | 仜 |
| 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 |
| N-2 | 亊 | 亊 | 仜 | 仜 | 仜 | 仜 | 仜 | 仜 |
| N-1 | 亊 | 仜 | 仜 | 仜 | 仜 | 仜 | 仜 | 仜 |
梋傝侾偲梋傝(俶亅侾)丄梋傝俀偲梋傝(俶亅俀)丄丒丒丒梋傝(俶亅侾)乛俀偲梋傝(俶亄侾)乛俀傪偦傟偧傟
儁傾偵偟偰丄慡堳偑偳偪傜偐堦曽偩偗偱傕傜偆偲偄偆偙偲偵偡傟偽偄偄傢偗偱偡丅
| 梋傝 | 俙1 | 俙2 | 丒丒丒 | 俙N/2 | 俙N/2+1 | 丒丒丒 | 俙N-1 | 俙N |
|---|---|---|---|---|---|---|---|---|
| 侾 | 仜 | 亊 | 亊 | 亊 | 亊 | 亊 | 亊 | 亊 |
| 俀 | 仜 | 仜 | 亊 | 亊 | 亊 | 亊 | 亊 | 亊 |
| 俁 | 仜 | 仜 | 仜 | 亊 | 亊 | 亊 | 亊 | 亊 |
| 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 |
| (N/2)-1 | 仜 | 仜 | 仜 | 亊 | 亊 | 亊 | 亊 | 亊 |
| N/2 | 仮 | 仮 | 仮 | 仮 | 仮 | 仮 | 仮 | 仮 |
| (N/2)+1 | 亊 | 亊 | 亊 | 仜 | 仜 | 仜 | 仜 | 仜 |
| 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 | 丒丒丒 |
| N-2 | 亊 | 亊 | 仜 | 仜 | 仜 | 仜 | 仜 | 仜 |
| N-1 | 亊 | 仜 | 仜 | 仜 | 仜 | 仜 | 仜 | 仜 |
愭傎偳偲摨條偵丄梋傝侾偲梋傝(俶亅侾)丄梋傝俀偲梋傝(俶亅俀)丄丒丒丒梋傝(俶乛俀)亅侾偲梋傝(俶乛俀)亄侾傪偦傟偧傟
儁傾偵偟偰丄慡堳偑偳偪傜偐堦曽偩偗偱傕傜偆偲偄偆偙偲偵偡傟偽偄偄傢偗偱偡丅
偟偐偟側偑傜梋傝(俶乛俀)偩偗偑扨撈偱巆偭偰偟傑偄傑偡丅
偦偙偱丄偙偙偩偗偼慡堳偱敿暘屄傪偟傑偡丅
僐儘僉僂儉幒
NO.508
偵娭楢偟偨榖戣偑偁傝傑偡丅
 栠傞
栠傞