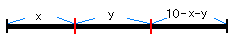
Weekend Mathematics／コロキウム室／1999.4〜6／NO.54

コロキウム室



NO.454　　　　'99 5/1 　　 Junko 　　　 三角形可能な確率（２）
　　

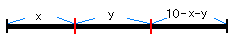
棒の長さを１０として、ｘ，ｙ，１０−ｘ−ｙの３つに分けたとします。
０＜ｘ＜１０、０＜ｙ＜１０−ｘとなります。

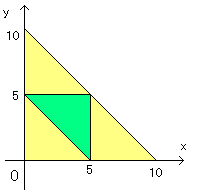
三角形ができるための条件は任意の２辺の長さの和が、 もう１辺の長さより長いことです。従って、以下の３条件となります。

  1. ｘ＋ｙ＞１０−ｘ−ｙ
    これより、ｙ＞５−ｘ
  2. ｘ＋(１０−ｘ−ｙ)＞ｙ
    これより、５＞ｙ
  3. ｙ＋(１０−ｘ−ｙ)＞ｘ
    これより、５＞ｘ
以上により、右図の黄緑の部分になります。
全事象(起こりうるすべてのケ−ス)は右図の大きい三角形ですから、 面積比のより三角形ができる確率は１／４となります。




NO.455　　　　'99 5/1 　　 Junko 　　　 不思議な級数（４）
　　

かの名著高木貞治の「解析概論」の中に、 これに関する記述がありましたので抜粋してここにまとめてみます。

無限級数Σａｎに対して、Σ|ａｎ|が収束するとき、 級数Σａｎは絶対収束するといいます。
級数Σａｎが絶対収束するならば、 もとの級数Σａｎも収束します。
Σａｎにおいて、正項をｐ１、ｐ２、・・・、 負項を−ｑ１、−ｑ２、・・・とかき、 ｐ＝Σｐｎ、ｑ＝Σｑｎとします。
ｐ、ｑが共に有限(≠∝)のときは、 Σ|ａｎ|＝ｐ＋ｑで絶対収束をしますからΣａｎも収束し、 Σａｎ＝ｐ−ｑとなります。

級数Σａｎが収束するけれども、絶対収束はしないというとき、 これを条件収束するといいます。
ｐ、ｑの一方だけが∝のときは、Σａｎが収束しないことになりますから、 条件収束のときは、ｐ、ｑ共に∝ということになります。 これについては、

条件収束する級数は、項の順序を適当に変更して任意の和に収束させたり、 また収束性を失わせたりすることができる。
と、Dirichlet(1829)が指摘したということです。

たとえば、Σａｎの項の順序を入れ替えて任意の正数ｃに収束させるのは どうするか？
正項ｐ１、ｐ２、・・・を順に加えて、 ｐαで初めてｃより大きくなったとする。
次に負項−ｑ１、−ｑ２、・・・を順に加えて、 −ｑβで初めてｃより小さくなったとする。
次にまた正項ｐα＋１、ｐα＋２、・・・を順に加えて、 ｐα＋γで初めてｃより大きくなったとする。
以下同様の作業を繰り返す。
(ｐ１＋ｐ２＋・・・＋ｐα)− (ｑ１＋ｑ２＋・・・＋ｑβ)＋ (ｐα＋１＋ｐα＋２＋・・・＋ｐα＋γ)−・・・
ｐ＝Σｐｎ＝∝、ｑ＝Σｑｎ＝∝ですから、 必ずｃを越えることは保証されています。
またｃを中心とした振れ幅は次第に小さくなり、いずれｃに収束していくわけです。

具体的な例が載っています。


(詳しくは「解析概論」　p.153)



NO.456　　　　'99 5/2 　　 プ−太 　　　xn+yn=zn（３）
　　






NO.457　　　　'99 5/3 　　 月の光 　　　定義域（１１）
　　

NO.272において次のような問題を出しました。


「関数の定義域を求めよ」という問題はよく目にしたので 普通だと思っていましたが、 junko先生や豊作さんの反応を見るとそうではないようでした。 このことについて次の文章を見つけました。
「オイラーの贈物」Ｐ.５１

オイラーは関数の定義域を”関数が数学的に意味を持つように、 暗黙のうちに定められるもの”とした。
略

このように、関数の定義とはまさに、定義を要するもので 「つぎの関数の定義域を求めよ」というような問題は、 定義域に対するオイラー流の解釈のもとではじめて成り立ち、 現代流に解釈すれば”定義を求める”という極めて奇妙な問いになってしまう。



NO.458　　　　'99 5/3 　　 月の光 　　　等速降下問題
　　

NO.415の最速降下問題の曲線の名称は サイクロイドです。
これについて類似の問題を出します。

ライプニッツの等速降下問題






NO.459　　　　'99 5/5 　　 Weadore 　　　三角形の確率（４）
　　

(一部訂正5/6)

こういう解答もあるという意味で別解（鋭角のみ）を書きます。

まず、最初に、円周上を(2n+1)等分する(2n+1)個の点から、 3点を選んで鋭角三角形になる確率を求めます。
円周を(2n+1)等分する点を順にP0,P1,P2 ......P2nとする。
ここで、3点A,B,Cを選んだ時にΔABCが鋭角三角形に なる確率を求める。
いま、A = P0として固定する。
この時、B,Cの選び方Nは N = 2nP2 = 2n(2n-1) [通り] −(*)
このうち、鋭角三角形になるのは、円の中心が ΔABCの内部にあるときだから、その数ｒは
B = Pk（1≦k≦n)の時のCの選び方が、 Pn+1 〜 Pn+kのk通りあるので、対称性から、 

r = 2 × (1+2+3+......+n)
  = n(n+1)  [通り]  −(**)
よって、(*),(**)より求める確率pは、






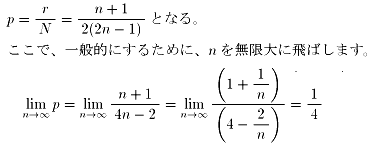
NO.460　　　　'99 5/5 　　 月の光 　　　オイラーなら？（２）
　　






NO.461　　　　'99 5/5 　　 月の光 　　　オイラーの「無限解析入門（１）」（６）
　　






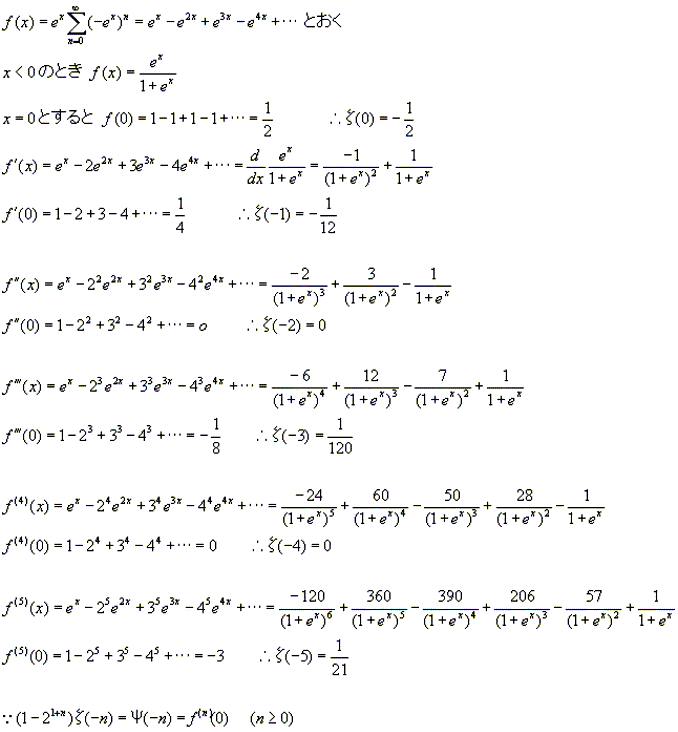
NO.462　　　　'99 5/5 　　 水の流れ 　　　ダーツの確率
　　

第１５回数学的な応募問題

太郎さんのお子さんは中学生です。次のような問題をもらって来ました。


  1. 三角形ＡＢＣにおいて、点Ａから辺ＢＣに垂線ＡＨを引きます。 このとき、三角形ＡＢＣの外接円の半径を、２辺の長さＡＢ，ＡＣと 垂線の長さＡＨで表しなさい。（図１参照）
  2. ある円において、点Ｐで直角に交わっている図２のような２本の弦ＡＣ、 ＢＤがあります。このとき、ＡＰ＝２，ＢＰ＝４，ＣＰ＝３でした。 この円の半径を求めなさい。（図２参照）
  3. ある円において、点Ｐで直角に交わっている図３のような２本の弦ＡＣ、 ＢＤがあります。このとき、ＡＰ＝ａ，ＢＰ＝ｂ，ＣＰ＝ｃ，ＤＰ＝ｄでした。 この円の半径を ａ，ｂ，ｃ，ｄを用いて表しなさい。（図３参照）


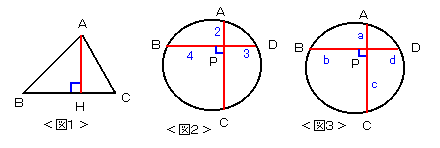
    太郎さんは、先日のゴールデンウイークにある電気店の大売り出しに 行って来ました。ここで、問題です。

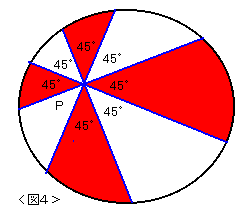
  4. この電気店では、当たりとはずれの場所が図４のような丸い的で ダーツ競技を行っていました。 的内の任意の点Ｐで交わる４本の弦を引き、 的を８つの部分に分けてありました。 ただし、４本の弦はそれぞれ４５度で交わっていました。 この８つの部分を交互に赤と白に４つに塗り分けてありました。 赤が当たりで、白がはずれです。 当たりである確率求めてください。

太郎さんは童心にかえって、ダーツ競技を楽しんでいましたが、 当たりとはずれの確率が気になってしかたがありません。 皆さんも、考えてください。　



NO.463　　　　'99 5/5 　　 Weadore 　　　タイル敷き
　　

問題
縦か横の長さが少なくとも一方は整数であるような、 色々なサイズの長方形タイルがある。 これらのタイルで 敷き詰める事のできる大きな長方形は縦か横のどちらか の長さが整数となる。
※答え方は積分を使う方法と使わない方法があります。 余裕があれば、二つ考えてみても面白いと思います。
これは結構難しい問題だと思います。(^^;







E-mail 戻る