Weekend Mathematics/コロキウム室/1999.1〜3/NO.47
NO.391 '99 3/10 月の光 ゼーター関数物語(31)
(一部記述にあやまりがありました。ごめんなさい。訂正junko3/11)

NO.392 '99 3/10 月の光 ゼーター関数物語(32)

NO.393 '99 3/10 水の流れ 宇宙空間での最短経路問題(6)
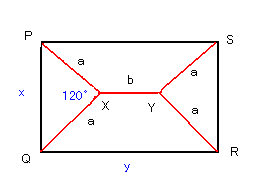
<1> 本題に入る前に平面上で、長方形PQRSを考えます。
短い辺の長さをPQ=x、長い辺の長さをQR=yとします。
ここで、図をみてください。
∠PXQ=∠PXY=∠QXY=120゜
∠RYS=∠RYX=∠SYX=120゜
となる点X、Yをみつけます。これがシュタイナー点です。
このとき、PX=a,XY=b として、a,bをx、yで表すと、
a=(x/2)÷cos30゜=x/√3,
b=y−x/√3
よって、4点P、Q、S、Tを結ぶ最短ネットワークは
4a+b=y+√3x
この場合 x=1,y=1 より
2(4a+b)+1=3+2√3≒6.464 となります。
勿論、これが求める最短経路ではありません。
この続きは明日にします。

NO.394 '99 3/11 月の光 ゼーター関数物語(33)

| 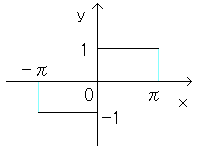
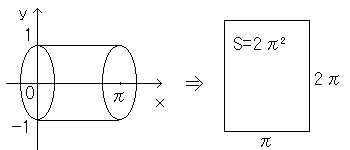 |
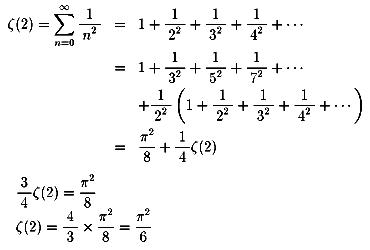


NO.395 '99 3/11 水の流れ 宇宙空間での最短経路問題(7)
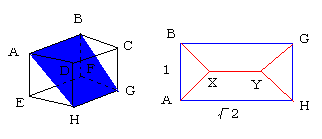
空間における最短経路<2>を送ります。
昨日、上面・底面ともシュタイナーのネットワークで結ばれて、
上面から底面までの高さ1を加えて、
(3+2√3)≒6.464 を求めました。
ところで、図のように長方形ABGHとCDEFにおいて、
4点のシュタイナーのネットワークを考えてみると、
前回の2(4a+b)=y+√3xに、x=1,y=√2を代入して =2(√2+√3) ≒6.292 となります。このとき、2つのネットワークは立方体のど真ん中で交わっています。

NO.396 '99 3/12 Junko ゼーター関数物語(34)
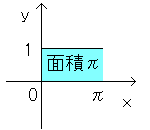
NO.394においては、
0<x<πにおける関数f(x)の回転体の表面積から導いています。
x=0,x=π,x軸,y=f(x)で囲まれた部分の面積からも導き出せます。
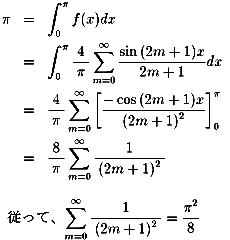

NO.397 '99 3/12 豊作 定義域(7)
NO.272 定義域(1)で出された問題は、結局「同
(2)、
(3)」
で解決
したのだろうか?
確かめたくても肝心の
問題文が意味不明なので
確かめようがない。

NO.398 '99 3/12 月の光 ゼーター関数物語(35)
NO.387
ゼーター関数物語第9夜の問題に対する答えです。
NO.394の中で示したように、
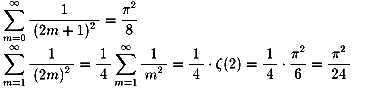

NO.399 '99 3/13 水の流れ 宇宙空間での最短経路問題(8)
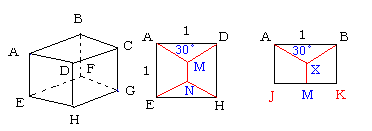
<3>前回は2つの平面AHGBとCDEFは45度で交わっています。
だから、この2つの平面の4点を結ぶシュタイナー点は立方体のど真ん中で
交わる2直線のなす角が90度になります。
あくまでも3点を結ぶ最短ネットワークはなす角が120度になっていなけれ
ばなりません。
だから、NO.393
<1>での上面ADCBと底面EHGFのネットワークにお
いて、上下の中央線の中点M、Nをすべて120度の角度を保ったまま立方体の
中心に引っ張っていきます。
これを横の面AEHDでみます。
平面ABXMは真横からみると、線AM上に重なっています。
そこで、横の面AEHDを結ぶ最短ネットワークも当然、
点M、Nは下がりながらシュタイナー点になります。
すると、図を見てください。
∠DAM=30°になります。
後は計算すれば求める結果になります。
ここからはコロキウム室の愛好者の皆さんに求めてもらいます。
お願いします。
なお、この最短ネットワークを発見したのはロウフボロフ大学の
ジョン・カストロ氏です。
それでは問題です。
「1辺1の正5角形の最短ネットワークの設計図とその長
さを求めてください。」
<参考文献:BLUE BACKSの数学パズル・パンドラの箱;講談社>

NO.400 '99 3/13 水の流れ ゴルフのスコア
太郎さんにはゴルフの好きな教え子がいます。
先日のことです。
15ホールを終わってちょうど84ストロークをたたいていました。
残り3ホールは16番パー3、17番パー4、18番パー5です。
さて、堅実な教え子は1ホールに対して、パー、ボギー、ダブルボギーの起こる可能性として、
1割、5割、4割の腕前です。
ここで、問題です。

NO.401 '99 3/13 月の光 ゼーター関数物語(36)
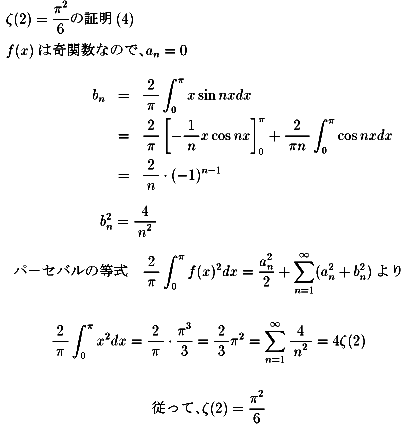

 E-mail
E-mail
 戻る
戻る