
Weekend Mathematics/コロキウム室/1999.1〜3/NO.38
NO.305 '99 1/22 浜田 明巳 A happy new year(2) NO.248の解答です。
答は以上の8個です。Aとwは交換可能でした。
少し答が多すぎるようです。
これはVISUAL BASICのプログラムで求めました。
問題 A 答 3 5 4 8
happy 10779 10779 10559 10559
new 425 423 738 734
-year -9208 -9208 -9302 -9302
−−−− −−−− −−−− −−−− −−−−
1999 1999 1999 1999 1999
6 8 7 9
10559 10559 10228 10228
738 736 369 367
-9304 -9304 -8605 -8605
−−−− −−−− −−−− −−−−
1999 1999 1999 1999
内容追加(1/23)
Option Explicit
Private Sub Command1_Click()
'A+happy+new-year=1999
Dim aa, h, a, p, y, n, e, w, r, kuriagari1, kuriagari2, kuriagari3 As Integer
For aa = 1 To 8 'A=aa
For y = 1 To 9
If y <> aa Then
For w = aa + 1 To 9 'Aとwは交換可能
If w <> y Then
r = (aa + y + w + 1) Mod 10 'A+y+w-r=9 (mod 10)
If r <> aa And r <> y And r <> w Then
kuriagari1 = aa + y + w - r
If kuriagari1 > 0 Then
kuriagari1 = kuriagari1 \ 10
ElseIf kuriagari1 < 0 Then
kuriagari1 = -1
End If
For p = 0 To 9
If p <> aa And p <> y And p <> w And p <> r Then
For e = 0 To 9
If e <> aa And e <> y And e <> w And e <> r And e <> p Then
a = (1 + p + e + kuriagari1) Mod 10 'p+e-a+kuriagari1=9 (mod 10)
If a <> aa And a <> y And a <> w And a <> r And a <> p And a <> e Then
kuriagari2 = p + e - a + kuriagari1
If kuriagari2 > 0 Then
kuriagari2 = kuriagari2 \ 10
ElseIf kuriagari2 < 0 Then
kuriagari2 = -1
End If
n = (19 - p + e - kuriagari2) Mod 10 'p+n-e+kuriagari2=9 (mod 10)
If n > 0 And n <> aa And n <> y And n <> w And n <> r And n <> p And n <> e And n <> a Then
kuriagari3 = p + n - e + kuriagari2
If kuriagari3 > 0 Then
kuriagari3 = kuriagari3 \ 10
ElseIf kuriagari3 < 0 Then
kuriagari3 = -1
End If
h = (1 - a + y - kuriagari3) / 10 '10*h+a-y+kuriagari3=1
If Int(h) = h And Abs(h - 5) < 5 And h <> aa And h <> y And h <> w And h <> r And h <> p And h <> e And h <> a And h <> n Then
Picture1.Print aa; "+"; h; a; p; p; y; "+"; n; e; w; "-"; y; e; a; r; "="; 1999
Picture1.Print w; "+"; h; a; p; p; y; "+"; n; e; aa; "-"; y; e; a; r; "="; 1999
End If
End If
End If
End If
Next
End If
Next
End If
End If
Next
End If
Next
Next
End Sub
Private Sub Command2_Click()
End
End Sub

NO.306 '99 1/22 Idaho Potato 分数の問題・その後(10)
No.281については、
残念ながら、私の問いかけの意図が伝わらなかったようですね。
解答1は、数学的に厳密に言うと、問題に対する答になっていないのです。
解答1を数学的に正しく完成するためには、
「x < -2 または x > 2」が「x > 2」の十分条件でないこと、
すなわち、
「x < -2 または x > 2」を満たすが「x > 2」を満たさない実数 x が存在することを(たとえば「x = -3 がそうである」という形で)述べなければなりません。
No.293の後半の、Junkoさんのご意見について。
要するに、「何かが存在することを示す」ためには、
その「存在する」というものの具体例を実際に示してみせれば、それで十分であって、
その具体例を「どうやって見つけたか」ということは、
数学的には「二の次」ということですね。
その意味では、
今回の「分数の問題」のような「存在を示せば十分」というタイプの問題に対して、
「その答に到達するまでの過程」を書くことを要求することは果たして妥当なのか、
ちょっと疑問を感じてしまいます。
私のように、たまたま「目の子」で答を見つけてしまった人は、
「答に到達するまでの過程」の書きようがありませんから。
なぜなら、解答1の1行目は、
命題の仮定「x2 > 4」を同値な条件「x < -2 または x > 2」に言い換えているだけで、
その言い換えられた形の仮定と、
もとの命題の結論「x > 2」との間の関係について、
一言も述べていないからです。
つまり、「したがって」という言葉の前後に、脈絡がないのです。
それをするぐらいなら、
解答2のように、最初から天下りに具体的な反例を与えるほうが、
すっきりした答になるわけです。
私の印象では、むしろ、
「受験のための数学」に毒されている多くの高校生や大学生は、
問題の意味を考えずに等式や同値変形といったテクニックで答を得ようとして、
いきおい解答1のような答になり、
解答2のような答え方に思い至らないのではないかと思います。
すでに述べたように、解答1はかっこいいように見えて、実は中身がないのです。
それに対して、解答2は、問題の意味をちゃんとわかっている人の答え方といえます。

NO.307 '99 1/23 Junko 等分点(2) 2000と互いに素であるものがいくつあるか数えればいいかと思います。
オイラ−関数を使って、ψ(2000)の値を求めることにします。
ψ(2000)=ψ(24×53)
=ψ(24)×ψ(53)
=(16-8)・(125-25)
=8・100
=800
オイラ−関数の計算に関しては、
NO.270ないし、
NO.273を参考にしてください。

NO.308 '99 1/23 みや 格子点(2) 格子点の問題の解答です。
点p(a、b)から原点に引いた直線が格子点を通らないと
y=(b/a)xがx<aで整数解をもたない。
すなわちa、bが互いに素であるということである。
そこで1から20の数の組みあわせで
互いに素である組み合わせが何通りあるかを数える。
i)a>bのとき
「水の流れ」さんのオイラー関数表より
互いに素の組み合わせ数=ψ(2)+ψ(3)+・・・ψ(20)=127
ii)a<bのとき
同様に127
iii)a=bのとき
p(1,1)のみ格子点を通らない。
格子点を通らない線分は127×2+1=255

NO.309 '99 1/23 Junko 格子点(3) この問題を考えると、「1と1は互いに素である。」という決め方は
合理的なのかなという気がしてきます。
割合を出すと、255/400=0.6375となります。

NO.310 '99 1/24 Junko 連続根号数その1(2)
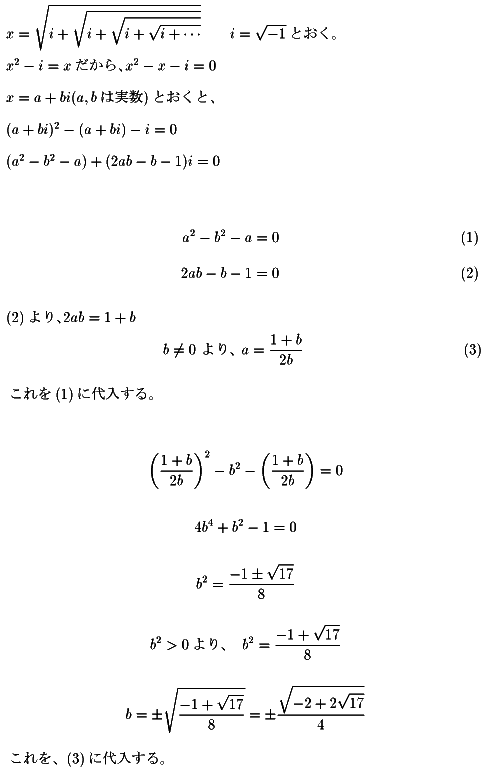
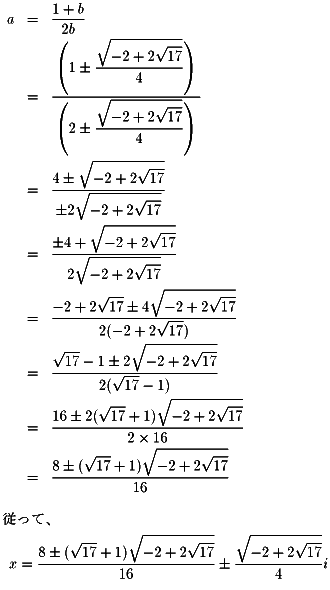

NO.311 '99 1/25 豊作 愛(?)のある問題(6)


NO.312 '99 1/26 Junko 連続根号数・その1(3) 虚数単位「i」を使った連分数が、複雑とはいえ(a+bi)という形の
複素数で表せるというのは何とも不思議な気もします。 虚数単位「i」はどうして生まれたか? 更に任意の複素数「c+di」に対して「x2=c+di」を満たす
複素数xを求めることもできます。
2次方程式「x2=−1」は実数の範囲には解がありません。
これに解を与えるために数の範囲を拡張し、「i」というものが考え出されました。
つまりi2=−1です。
次にこの「i」を使って2次方程式「x2=i」を解こうとすると
さらに数の範囲を拡張しなければならないのではないか?
同じことをどんどん繰り返すと限りなく数の範囲が広がって収拾がつかなくなるのでは
ないか? と思いきや、そんなことはないのです。
2つの実数a,bと虚数単位iを使って、「a+bi」と表せる数を複素数といいます。
b=0のときを実数、b≠0のときを虚数と呼びます。
数の範囲を複素数にまで拡張すれば、もうこれで充分です。
先程の2次方程式「x2=i」を解いてみます。
x=a+biとおきます。
(a+bi)2=i
a2+2abi+b2i2=i
(a2−b2)+(2ab−1)i=0
a2−b2=0 かつ 2ab−1=0
これを解くと、a=b=±√2/2となります。
従って、x=±(√2/2+√2/2i)というわけです。
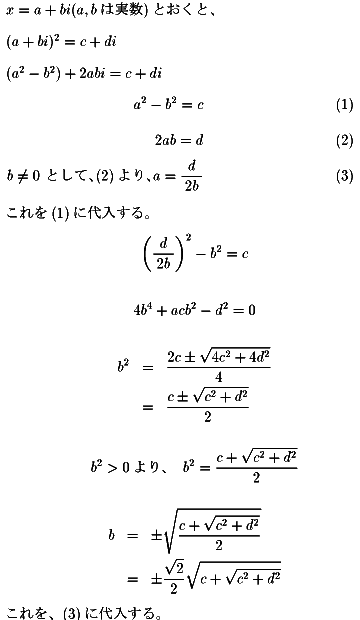
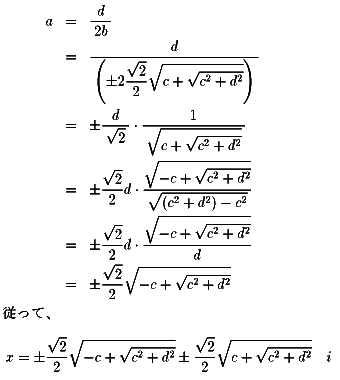

NO.313 '99 1/29 水の流れ 宇宙空間での最短経路問題(1) 太郎さんは、このたび、宇宙空間における8つの研究施設を
結ぶ最短経路の設計図を依頼されました。
この施設は、1辺が10mの立方体の 各頂点にあります。
これらすべての施設をつなぐ最短の長さと設計図を作ってください。
もちろん設計図ですので、施設は点で、最短経路は線として、考えてください。
依頼を受けた太郎さんはどの経路が最短になるか分かりませんので、
数種類の設計図を作って、もっていくつもりです。
あなたは、どんな設計図を作りますか、考えてください。

NO.314 '99 1/29 水の流れ 立方体の展開 みなさん、1辺の長さ10cmの立方体を作ってください。
それを辺に沿って切り開くと、
6つの正方形が辺と辺でくっついた形の展開図にすることができます。
で、この展開図のとき、切り開いた周の長さの合計は70cmになります。
そこで、太郎さんは立方体の面を切り開いて、
斬新的な展開図を考えました。
それは、切断する長さが最も短くなるように立方体を切って
平面に展開する方法でした。
太郎さんが考えた斬新的な展開方法を考えてください。
ヒント:正方形における最短シュタイナー問題の
解答NO.210を参考にしてください。
皆さんが考えた、いろいろな設計図や展開図をも、教えてください。

 E-mail
E-mail
 戻る
戻る