Weekend Mathematics/コロキウム室/1998.7〜12/NO.27
コロキウム室
NO.210 11/22 情報処理科2年 最短シュタイナー問題(4)
NO.180の問題2
正方形の頂点A,B,C,Dの位置に4校があり、
この4校を連結するネットワーク
(どの2校もネットワークを通して、行き来できるようにする)
を結ぶ計画があります。
もっとも短い結び方で、何kmが必要でしょうか?
また、その、作図も書いてください。
ただし、1辺の距離をakmとする。
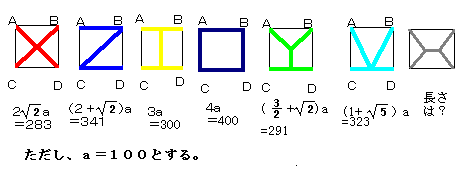
授業の中で出題されたこの問題について、
皆で考えました。
これら設計図の中で、一番短いのは対角線の×印のネットです。
一番右は図だけで、長さは出ていません。
定規で測ってみたら、一番左のものが、対角線の1辺を10cmとして、
だいたい、2√2×10=28.3センチになりました。
次ぎに、一番右はというと、どうも28.3センチより短いみたいです。
でも、途中の交点はどこに取ると良いか?
また、なぜ?と問われると答えられません。

NO.211 11/22 水の流れ 大相撲本場所(6)
参考図のようなパスカルの三角形(二項係数)を斜めに足すと、
フィボナッチ数列になります。
<参考図> パスカルの三角形(二項係数)
| nCr
| 0 | 1 | 2 | 3
| 4 | 5 | 6 | 7 |
| 0
| 1 | | |
| | | | |
| 1
| 1 | 1 | |
| | | | |
| 2
| 1 | 2 | 1 |
| | | | |
| 3
| 1 | 3 | 3 | 1
| | | | |
| 4
| 1 | 4 | 6 | 4
| 1 | | | |
| 5
| 1 | 5 | 10 | 10
| 5 | 1 | | |
| 6
| 1 | 6 | 15 | 20
| 15 | 6 | 1 | |
| 7
| 1 | 7 | 21 | 35
| 35 | 21 | 7 | 1 |
数式でかくと、次のようになります。
フィボナッチ数列をF(n)とすると、F(1)=1、F(2)=1、F(3)=1+1=2、
F(4)=1+2=3、F(5)=2+3=5、・・・
F(n+1)=nC0+n−1C1+
n−2C2+・・・+mCm
F(n+2)=n+1C0+nC1+
n−1C2+・・・+m+1Cm
ただし、n=2mで、m≧1、n≧2の自然数とする。2つの組みで考える。

NO.212 11/23 naomi Alphabetの問題・Part2(2)
答え S S になりますか。
答えの後もずっと続くようになっているのがヒントになりました。

NO.213 11/25 Junko 大相撲本場所(7)
NO.211にあるパスカルの三角形を見て、
本当にびっくり、感激しました。
確かに斜めに足していくとフィボナッチ数が現れてきます。
こんなところでつながっているとは! 神秘を感じます。

NO.214 11/25 水の流れ 大相撲本場所(8)
大相撲の問題の続きです。
もし、3連敗しない方法(2連敗まで許される)場合は
1,2,3,4,・・・、15日ではどんな数列に
なるでしょう。長方形の問題ではどんな変化になるでしょう?

NO.215 11/28 ヴァー 大相撲本場所(9)
水の流れさんのNo.211の主張が,その主張どおりフィボナッチ数列の式「F(n)+F(n+1)=F(n+2)」を満たしていることを証明してみましょう.
この証明では,組合せ「nCr」について常に成り立つ等式(恒等式)
nCr+nCr+1=n+1Cr+1
を利用します.
< F(2m)+F(2m+1)=F(2m+2) の証明 >
まず,No.211から,
|
F(2m)
|
=
|
|
|
2m-1C0
|
+
|
2m-2C1
|
+
|
..
|
+
|
mCm-1
|
|
F(2m+1)
|
=
|
2mC0
|
+
|
2m-1C1
|
+
|
2m-2C2
|
+
|
..
|
+
|
mCm
|
|
|
であり,この2つの式を足し合わせると,
で,
|
右辺
|
=
|
2mC0
|
|
|
|
+(2m-1C0+2m-1C1)
|
|
|
|
+(2m-2C1+2m-2C2)
|
|
|
|
+...
|
|
|
|
+(mCm-1+mCm)
|
|
|
=
|
2m+1C0+2mC1+2m+1C2+...+m+1Cm
|
|
|
=
|
F(2m+2)
|
になります.
ここでは,はじめの項では,2mC0=2m+1C0を用いていて,( )の部分では先の等式を用いています.
<F(2m+1)+F(2m+2)=F(2m+3) の証明 >
先程と同じく,No.211から,
|
F(2m+1)
|
=
|
|
|
2mC0
|
+
|
2m-1C1
|
+
|
..
|
+
|
m+1Cm-1
|
+
|
mCm
|
|
|
|
F(2m+2)
|
=
|
2m+1C0
|
+
|
2mC1
|
+
|
2m-1C2
|
+
|
..
|
+
|
m+1Cm
|
であり,この2つの式を足し合わせると,
で,
|
右辺
|
=
|
2m+1C0
|
|
|
|
+(2mC0+2mC1)
|
|
|
|
+(2m-1C1+2m-1C2)
|
|
|
|
+...
|
|
|
|
+(m+1Cm-1+m+1Cm)
|
|
|
|
+mCm
|
|
|
=
|
2m+2C0+2m+1C1+2mC2+...+m+2Cm+m+1Cm+1
|
|
|
=
|
F(2m+3)
|
になります.
ここでは,はじめの項では,2m+1C0=2m+2C0を用いていて,同じように最後の項では,mCm=m+1Cm+1を用いています.
また,( )の部分では先の等式を用いています.
この証明は,No.211の表に対応させると次のようなことを表しています.
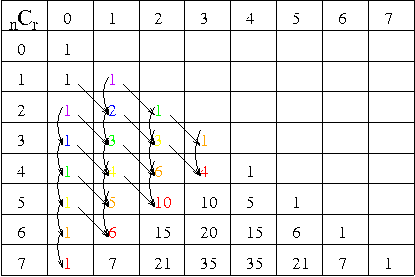
例えば,赤の部分は,黄色とオレンジの数字の和になっていることを表しています.
同じマスに2つの矢印が流れ込んでいるのがその「和」になっていることを示しています.

 E-mail
E-mail
 戻る
戻る
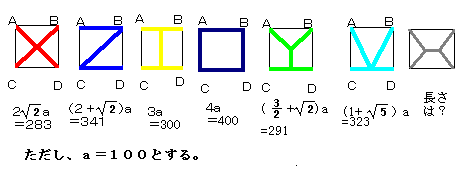


 E-mail
E-mail
 戻る
戻る