
Weekend Mathematics乛僐儘僉僂儉幒乛1999.1乣3乛NO.37
NO.295 丂丂丂 '99 1/20 丂丂悈偺棳傟 丂丂丂 楢懕帺慠悢偺榓乮俀乯 侾俆偺婏悢偺栺悢偼侾丆俁丆俆丆侾俆偺係屄偱偡偐傜丄
丂侾俆亖侾俆
丂侾俆亖俈亄俉
丂侾俆亖係亄俆亄俇
丂侾俆亖侾亄俀亄俁亄係亄俆
偺係庬椶偵暘夝偱偒傑偡丅
丂乽堦斒偵丄惍悢俶傪楢懕偟偨偄偔偮偐偺帺慠悢偵暘夝偡傞曽朄偼
俶偺婏悢偺栺悢偺屄悢偵摍偟偄偺偱偡乿
偩偐傜丄Junko偝傫偑尵傢傟傞傛偆偵丄俶亖俀倣偺応崌偼晄壜擻偱偡丅

NO.296 丂丂丂 '99 1/20 丂丂Junko 丂丂丂 楢懕帺慠悢偺榓乮俁乯 惍悢俶傪楢懕偟偨偄偔偮偐偺帺慠悢偵暘夝偡傞曽朄傪
俶偺惈幙偵傛偭偰暘椶偟側偑傜帵偟傑偡丅
[倶]偼僈僂僗婰崋傪昞偟傑偡丅
偙傟偼倶傪墇偊側偄嵟戝偺惍悢傪梌偊傑偡丅 俶亖侾俆偺暘夝偵偮偄偰丄
扨撈丄栺悢俁傪傕偮偐傜俁偮偵暘夝偱偒傞丄
栺悢俆傪傕偮偐傜俆偮偵暘夝偼偄偄偲偟偰丄
栺悢侾俆傪傕偮偙偲偲丄侾俆亖俈亄俉偲偺暘夝傪
偳偆娭楢偯偗偰偄偄偺偐傢偐傜側偄偺偱偡丅 傑偨俶亖侾侾侾偺暘夝偵偮偄偰丄侾侾侾亖俁亊俁俈傛傝丄
扨撈丄栺悢俁傪傕偮偐傜俁偮偵暘夝偱偒傞(111=36+37+38)丄
婏悢偩偐傜俀偮偵暘夝偱偒傞(111=55+56丄慜抜偱尵偭偨偙偲)偼偄偄偲偟偰丄
栺悢俁俈傪傕偮偐傜俁俈偵暘夝偱偒傞丄偲偄偆傢偗偵偼偄偐側偄偲巚偆偺偱偡丅
嫮堷偵傗傞側傜丄
偙偆偟偰峫偊偰偄偔偲丄乽悈偺棳傟乿偝傫偺偍偭偟傖偭偰偄傞
俶亖[俶乛俀]亄([俶乛俀]亄侾)偲偱偒傞偐傜偱偡丅
偨偲偊偽丄侾俆亖俈亄俉偺傛偆偵丅
俶亖([俶乛俁]亅侾)亄[俶乛俁]亄([俶乛俁]亄侾)偲偱偒傞偐傜偱偡丅
偮傑傝丄俶傪傑偢俁摍暘偟傑偡丅侾俆亖俆亄俆亄俆
恀傫拞傪拞怱偵愭摢偼侾傪堷偒丄嵟屻偼侾傪懌偡丅侾俆亖係亄俆亄俇
偨偩偟丄[俶乛俁]亅侾亞侾傛傝丄俶亞俇
俶亖([俶乛俆]亅俀)亄([俶乛俆]亅侾)亄[俶乛俆]亄([俶乛俆]亄侾)亄([俶乛俆]亄俀)偲偱偒傞偐傜偱偡丅
偮傑傝丄俶傪傑偢俆摍暘偟傑偡丅侾俆亖俁亄俁亄俁亄俁亄俁
恀傫拞傪拞怱偵慜敿偼侾偯偮堷偒丄屻敿偼侾偯偮傪懌偟傑偡丅
侾俆亖侾亄俀亄俁亄係亄俆
偨偩偟丄[俶乛俆]亅俀亞侾傛傝丄俶亞侾俆
俶亖俶乛俀亄俶乛俀 (偙偙偱丄俶乛俀偼婏悢偱偡偐傜丄倝偺侾傛傝)
丂亖{[俶乛係]亄([俶乛係]亄侾)}亄{[俶乛係]亄([俶乛係]亄侾)}
丂亖{[俶乛係]亄([俶乛係]亄侾)}亄{([俶乛係]亅侾)亄([俶乛係]亄俀)}
丂亖([俶乛係]亅侾)亄[俶乛係]亄([俶乛係]亄侾)亄([俶乛係]亄俀)
偲偱偒傑偡丅
椺偊偽丄侾侽亖俆亄俆
丂丂丂丂丂丂亖(俀亄俁)亄(俀亄俁)
丂丂丂丂丂 亖(俀亄俁)亄(侾亄係)
丂丂丂丂丂丂亖侾亄俀亄俁亄係
偨偩偟丄[俶乛係]亅侾亞侾傛傝丄俶亞俉偱偡丅
俶亖俶乛係亄俶乛係亄俶乛係亄俶乛係
丂丂 (偙偙偱丄俶乛係偼婏悢偱偡偐傜丄倝偺侾傛傝)
丂亖{[俶乛俉]亄([俶乛俉]亄侾)}亄{[俶乛俉]亄([俶乛俉]亄侾)}亄{[俶乛俉]亄([俶乛俉]亄侾)}亄{[俶乛俉]亄([俶乛俉]亄侾)}
丂亖{[俶乛俉]亄([俶乛俉]亄侾)}亄{([俶乛俉]亅侾)亄([俶乛俉]亄俀)}亄{([俶乛俉]亅俀)亄([俶乛俉]亄俁)}亄{([俶乛俉]亅俁)亄([俶乛俉]亄係)}
丂亖([俶乛俉]亅俁)亄([俶乛俉]亅俀)亄([俶乛俉]亅侾)亄[俶乛俉]亄([俶乛俉]亄侾)亄([俶乛俉]亄俀)亄([俶乛俉]亄俁)亄([俶乛俉]亄係)
偲偱偒傑偡丅
椺偊偽丄係係亖侾侾亄侾侾亄侾侾亄侾侾
丂丂丂丂丂丂亖(俆亄俇)亄(俆亄俇)亄(俆亄俇)亄(俆亄俇)
丂丂丂丂丂 亖(俆亄俇)亄(係亄俈)亄(俁亄俉)亄(俀亄俋)
丂丂丂丂丂丂亖俀亄俁亄係亄俆亄俇亄俈亄俉亄俋
偨偩偟丄[俶乛俉]亅俁亞侾傛傝丄俶亞俁俀偱偡丅
乽堦斒偵丄惍悢俶傪楢懕偟偨偄偔偮偐偺帺慠悢偵暘夝偡傞曽朄偼
俶偺婏悢偺栺悢偺屄悢偵摍偟偄乿偲偄偆偺傕偆側偯偗傞偺偱偡偑丄
媈栤傕惗偠傑偡丅
侾侾侾亖俁亄俁亄俁亄丒丒丒亄俁(俁俈屄)
丂丂丂亖(俁亄俁亄丒丒丒亄俁)亄俁亄(俁亄俁亄丒丒丒亄俁)
丂丂丂亖{(-15)亄(-14)亄丒丒丒亄俀}亄俁亄{係亄丒丒丒亄俀侽亄俀侾}
偱傕丄晧偺悢偼偩傔偱偡傛偹丅愭掱弎傋偨俶偼偁傞掕悢埲忋偲偄偆忦審偵傂偭偐偐傞傢偗偱偡丅
巹偼偲傫偱傕側偔尒摉堘偄側峫偊曽傪偟偰偄傞偺偱偟傚偆偐丠丂
傕偭偲暿側暘夝偺巇曽偑偁傞偺偱偟傚偆偐丠

NO.297 丂丂丂 '99 1/20 丂丂僐僂僗働 丂丂丂 1999!偺寘悢乮侾乯 傛偭偰丄侾俋俋俋両偼係俇侽侾寘丄係俇侽俀寘丄係俇侽俁寘偺偄偢傟偐偱偁傞丅
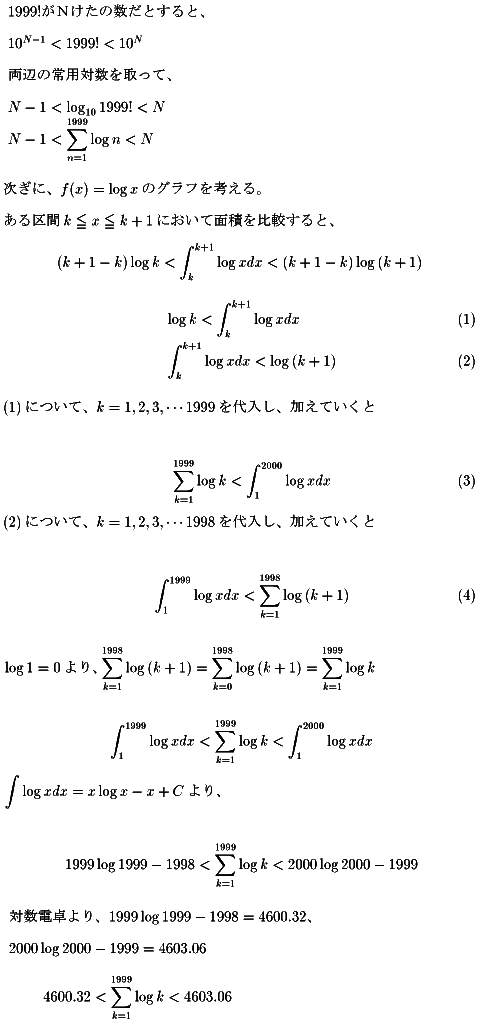
偙傟埲忋偱偒側偄丒丒丒偳偆偡傟偽惓偟偄摎偊偵偨偳傝拝偗傞偺偱偟傚偆偐丠

NO.298 丂丂丂 '99 1/20 丂丂Junko 丂丂丂 1999!偺寘悢乮俀乯 姶怱偟傑偟偨丄偡偛偄敪憐亄寁嶼偱偡偹両
娭悢偺僌儔僼偲倶幉偲偱埻傑傟偨柺愊傪弌偡偺偵丄
撪懁偺拰廤抍偲奜懁偺拰廤抍偺柺愊偱偼偝傒丄
偦偺墶暆傪彫偝偔偟偰偄偔(嬌尷傪偲傞)偙偲偱媮傔傞偲偄偆偙偲偑偁傝傑偡丅
偟偐偟偙偺応崌偼媡偵拰廤抍偺柺愊傪媮傔傞偺偵丄
y=log x 偺掕愊暘偱嬤帡偡傞偲偄偆偙偲偱偡偹丅
偨偩偟侾儢強丄寁嶼傑偪偑偄傪偟偰偄傑偡丅

廬偭偰丄壜擻惈偼俆俈俁侾丄俆俈俁俀丄俆俈俁俁偲側傝傑偡丅
偱偡偐傜丄摎偊偑侾偮偵寛傑傜側偄偲偄偆栤戣偼憡曄傢傜偢夝寛偟傑偣傫丅
偙傟偼丄偙偺曽朄偱偼巇曽偑側偄傛偆偵巚偄傑偡丅
偙偺惛搙傪忋偘傞偵偼丄柺愊偱偼偝傓帪偺柍懯傪彮側偔偡傞岺晇傪
偟偰偄偐側偗傟偽側傜偢丄偙傟偼傓偢偐偟偄傛偆偵巚偄傑偡丅
墌廃棪兾傪媮傔傞偺偵丄撪懁偲奜懁偐傜惓懡妏宍偱偣傔偰偄偭偨偙偲傪楢憐偝偣傑偡偹丅
場傒偵丄乽mathematica乿偱寁嶼偟傑偟偨傜丄
log10侾俋俋俋両亖俆俈俁俀丏俀俀ゥ苽葌鑲軅祩絺虃艁A俆俈俁俁寘偲偄偆偙偲偵側傝傑偡丅
崱寧偺栤戣丂侾俋俋俋擭偺栤戣偼丄
偙偺俆俈俁俁寘偺偆偪壓偐傜壗寘傑偱侽偑暲傇偱偟傚偆偐丠丂偲偄偆栤戣偱偡丅

NO.299 丂丂丂 '99 1/21 丂丂悈偺棳傟 丂丂丂 楢懕帺慠悢偺榓乮係乯
侾俆亖侾亊侾俆
丂丂亖侾亄侾亄侾亄侾亄侾亄侾亄侾亄侾亄侾亄侾亄侾亄侾亄侾亄侾亄侾
丂丂亖亅俇亅俆亅係亅俁亅俀亅侾亄侽亄侾亄俀亄俁亄係亄俆亄俇亄俈亄俉
丂丂亖(亅俇亅俆亅係亅俁亅俀亅侾亄侽亄侾亄俀亄俁亄係亄俆亄俇)亄俈亄俉
丂丂亖侽亄俈亄俉
丂丂亖俈亄俉
偲側傝丄榓偼侽偱偡偐傜丅偦偺榓偼侾俆偱曄傢傜側偄偺偱偡丅
侾侾侾亖俁亄俁亄俁亄丒丒丒亄俁(俁俈屄)
丂丂丂亖(俁亄俁亄丒丒丒亄俁)亄俁亄(俁亄俁亄丒丒丒亄俁)
丂丂丂亖{(-15)亄(-14)亄丒丒丒亄俀}亄俁亄{係亄丒丒丒亄俀侽亄俀侾
丂丂丂亖{(-15)亄(-14)亄丒丒丒侾係亄侾俆}亄侾俇亄侾俈亄侾俉亄侾俋亄俀侽亄俀侾
丂丂丂亖侽亄侾俇亄侾俈亄侾俉亄侾俋亄俀侽亄俀侾
丂丂丂亖侾俇亄侾俈亄侾俉亄侾俋亄俀侽亄俀侾
晧偺悢偺張抲傪偳偆偡傞偐偩偗偱偟偨丅

NO.300 丂丂丂 '99 1/21 丂丂悈偺棳傟 丂丂丂 楢懕帺慠悢偺榓乮俆乯 乽堦斒偵丄惍悢俶傪楢懕偟偨偄偔偮偐偺帺慠悢偵暘夝偡傞
曽朄偼俶偺婏悢偺栺悢偺屄悢偵摍偟偄丅乿 亙徹柧亜俶偑偁傞婏悢偺栺悢乮俀倠亄侾乯傪帩偮偲偒丄
乮偨偩偟丄倠偼惍悢乯 媡偵丄侾捠傝偺楢懕悢偑偁偭偨偲偒丄侾屄偺婏悢偑偁傞偩傠偆偐丠
倎亊乮俀倠亄侾乯亖俶偲側傞倎傪乽恀傫拞乿偲偟偰楢懕悢偑嶌傟傞丅
偦偙偱丄倎傪乽恀傫拞乿偲偟偰丄倣傪嵟彫悢丄俵傪嵟戝悢偲偡傞丅
俶亖倣亄乮倣亅侾乯亄丒丒丒亄倎亄丒丒丒亄乮俵亅侾乯亄俵丒丒丒嘆
偙傟偼丄倎偺嵍懁偼倠屄丄倎偺塃懁偼倠屄丄偦偟偰丄恀傫拞偺侾屄
偺崌寁乮俀倠亄侾乯屄偺悢偑暲傫偱偄傞丅
傕偟丄倣偑晧偺悢偺偲偒偵偼丄彮偟峫偊偰傒傑偡丅
倣亄乮倣亅侾乯亄丒丒丒亄侽亄丒丒丒亄乮亅倣亅侾乯亄乮亅倣乯亖侽丂丒丒丒嘇
傛傝丄嘆亅嘇亖俶亅侽亖俶
偡側傢偪丄乮亅倣亄侾乯亄丒丒丒亄乮俵亅侾乯亄俵亖俶丂丒丒丒嘊
偙傟偼丆惓偺悢偩偗偱嶌偭偨楢懕悢偺榓偱偡丅
偲偙傠偱丄嘆偺宍偱偮偔偭偨楢懕偺榓偼摉慠乽婏悢屄乿偱偡丅
嘊偺応崌偼丄嘆偺婏悢屄偐傜丄嘇偺婏悢屄傪堷偒傑偡偐傜丄
摉慠乽嬼悢屄乿偺楢懕悢偺榓偱偡丅
埲忋偐傜丄侾屄偺婏悢偺栺悢偐傜丄昁偢嘆傑偨偼嘊偺宍偺侾捠傝偺楢懕悢偺榓偑摼傜傟傑偡丅
丂
挷傋傑偡丅
侾捠傝偺楢懕悢偑梌偊傜傟偨偲偒丄偦傟偼嘆偐嘊偺偳偪傜偐偺宍偱偡丅
嘆側傜丄婏悢屄傛傝丄恀傫拞偺悢偑侾偮懚嵼偟偰丄偦傟偵墳偠偰婏悢侾偮偑寛傑傞丅
嘊側傜丄嬼悢屄偩偐傜丄嘇偺婏悢屄傪嶌偭偰丄
嘆偺晧偐傜巒傑傞婏悢屄偺榓傪偮偔傞丅
偙偺偲偒丄恀傫拞偺悢偑侾偮懚嵼偟偰丄
偦傟偵墳偠偰丄懠偺暿偺婏悢偑侾偮偑寛傑傞丅
偟偨偑偭偰丄乽婏悢偺栺悢乿偲乽惓偺楢懕悢偺榓乿偼侾懳侾偵懳墳偟偰丄
偦偺屄悢偼堦抳偡傞丅丂丂丂亙徹柧廔傢傝亜

NO.301 丂丂丂 '99 1/21 丂丂償傽亅 丂丂丂 屳偄偵慺乮俉乯 悈偺棳傟偝傫偺摎偊(NO.263)偵傛傞偲
冋(2)+.....+冋(100) = 3043側偺偱丆
(冋(2)+.....+冋(100))/(100(100-1)/2) = 3043*2/100/99 = 3043/4950
偲側偭偰丆巹偺6087/10000偲偼堘偭偰偄傑偡丏
偙傟偼丆悈偺棳傟偝傫偱偼丆杔偺恾(NO.289)偱偄偆偲丆
嵍壓偐傜塃忋偵岦偐偆懳妏慄傛傝壓敿暘偺晹暘偺敀崟傪
峫偊偰偄傞偙偲偵側偭偰偄傞偐傜偱偡丏
偮傑傝丆6087=3043*2+1丆側傫偱偡偑丆
偙傟偼3043偑壓敿暘偺崟偺屄悢側偺偱偦傟傪2攞偟偰忋敿暘偺崟傑偱峫椂偟丆
嵟屻偵(x,y)=(1,1)偺晹暘偺崟傪晅偗壛偊偰偄傞傢偗偱偡

NO.302 丂丂丂 '99 1/21 丂丂Junko 丂丂丂 屳偄偵慺乮俋乯 乽擟堄偵帺慠悢傪俀偮慖傇帪丄乿偲偁傝傑偡偑丄偦偺慖傃曽偵傛偭偰堘偭偰偔傞傢偗偱偡偹丅
摨偠傕偺傪俀偮慖傇偙偲傪嫋偟丄偝傜偵偦偺弴彉傕峫椂偡傞(廳暋弴楍)偲丄 侾搙偵俀偮偺帺慠悢傪偲傞(慻傒崌傢偣丄摨偠傕偺偳偆偟偼偁傝偊側偄)偲丄
慡晹偱侾侽侽俀亖侾侽侽侽侽捠傝偱偡丅
偦偺偆偪偺俇侽俉俈捠傝偱偡偐傜丄俇侽俉俈乛侾侽侽侽侽
侾侽侽俠俀亖侾侽侽丒俋俋乛俀亖係俋俆侽
偦偺偆偪偺俁侽係俁偱偡偐傜丄俁侽係俁乛係俋俆侽

NO.303 丂丂丂 '99 1/22 丂丂丂丂悈偺棳傟 丂丂丂 1998攞悢偺栤戣乮俁乯 NO.184偺俁丏乽楢懕偡傞帺慠悢倰屄偺愊偼倰両偱妱傝愗傟傞乿偺暿徹柧偱偡丅
亙徹柧亜慻傒崌傢偣値俠倰亖値両乛倰両乮値亅倰乯両丂傪峫偊傞丅
偙偙偱丄擟堄偺慺悢倫偑暘巕偺値両偵娷傑傟傞屄悢傪値乮倫乯偲丄
暘曣偺倰両乮値亅倰乯両偵娷傑傟傞屄悢傪倰乮倫乯亄倱乮倫乯偲偍偄偰丄
斾傋傑偡丅
偨偩偟丄倰乮倫乯偼倰両偵娷傑傟傞慺悢倫偺屄悢丄
倱乮倫乯偼乮値亅倰乯両偵娷傑傟傞慺悢倫偺屄悢偲偡傞丅
偩偐傜丄偳傫側倫偵偨偄偟偰傕丄値乮倫乯亞倰乮倫乯亄倱乮倫乯傪帵偣傟偽椙偄偺偱偡丅
乵丂丂乶偼僈僂僗婰崋偱偡丅
値(倫)亖乵値/倫乶亄乵値/倫2乶亄乵値/倫3乶亄乵値/倫4乶亄丒丒丒
倰(倫)亖乵倰/倫乶亄乵倰/倫2乶亄乵倰/倫3乶亄乵倰/倫4乶亄丒丒丒
倱(倫)亖乵倱/倫乶亄乵倱/倫2乶亄乵倱/倫3乶亄乵倱/倫4乶亄丒丒丒
偨偩偟丄倱亖値亅倰丆値亖倰亄倱偙偙偱丄
僈僂僗婰崋偺惈幙偲偟偰丄
堦斒偵乵乮倎亄倐乯乛倠乶亞乵倎乛倠乶亄乵倐乛倠乶偑惉傝棫偪傑偡偺偱丄
偙傟傛傝丄柧傜偐偵丄値乮倫乯亞倰乮倫乯亄倱乮倫乯偑惉傝棫偪傑偡丅
偟偨偑偭偰丄暘曣偼偡傋偰丄栺暘偝傟偰丄値俠倰偼惍悢偲側傞丅
偡側傢偪丄値俠倰亖値(値亅侾)(値亅俀)丒丒丒(値亅倰亄侾)乛倰両
傛傝丄戣堄偼徹柧偝傟偨丅

NO.304 丂丂丂 '99 1/22 丂丂丂丂悈偺棳傟 丂丂丂 僷僗僇儖偺嶰妏宍乮俁乯 乽倫偑慺悢側傜丄僷僗僇儖偺嶰妏宍偺椉抂偺侾埲奜偼
倫偱妱傝愗傟傞乿偙偲偵傕婥偑偮偒傑偟偨丅
亙徹柧亜値俠倰亖値両乛倰両乮値亅倰乯両
偵偍偄偰丄摿偵慺悢倫偵懳偟偰丄
倫俠倰亖倫両乛倰両乮倫亅倰乯両
偙傟偼丄惍悢偱偡偺偱丄侽亙倰亙倫側傜偽丄
暘巕偵倫偑偁傝丄暘曣偵偼倫偲偄偆場悢偼娷傑傟偰偄傑偣傫丅
偟偨偑偭偰丄倫偑慺悢側傜偽丄値俠倰丄
乮侽亙倰亙倫乯偼倫偺攞悢偱偁傞丅
亙徹柧廔傢傝亜

 E-mail
E-mail
 栠傞
栠傞